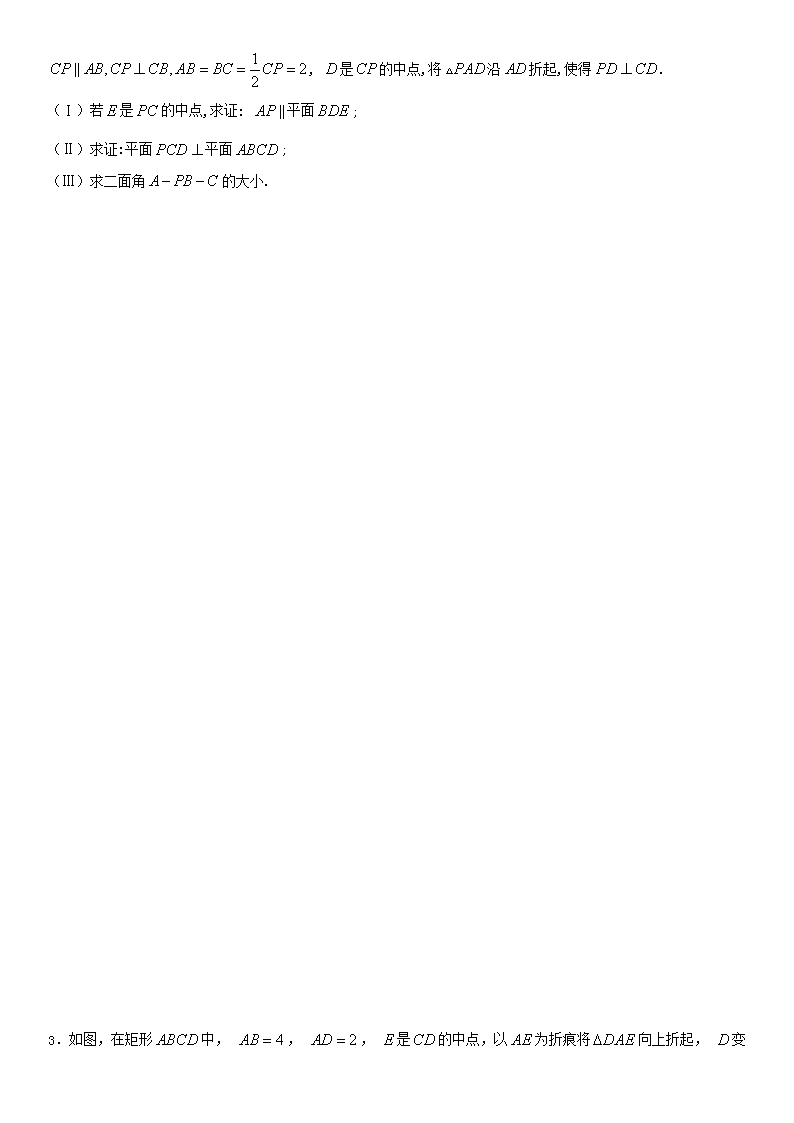高考数学立体几何理科专题01线面角 13页

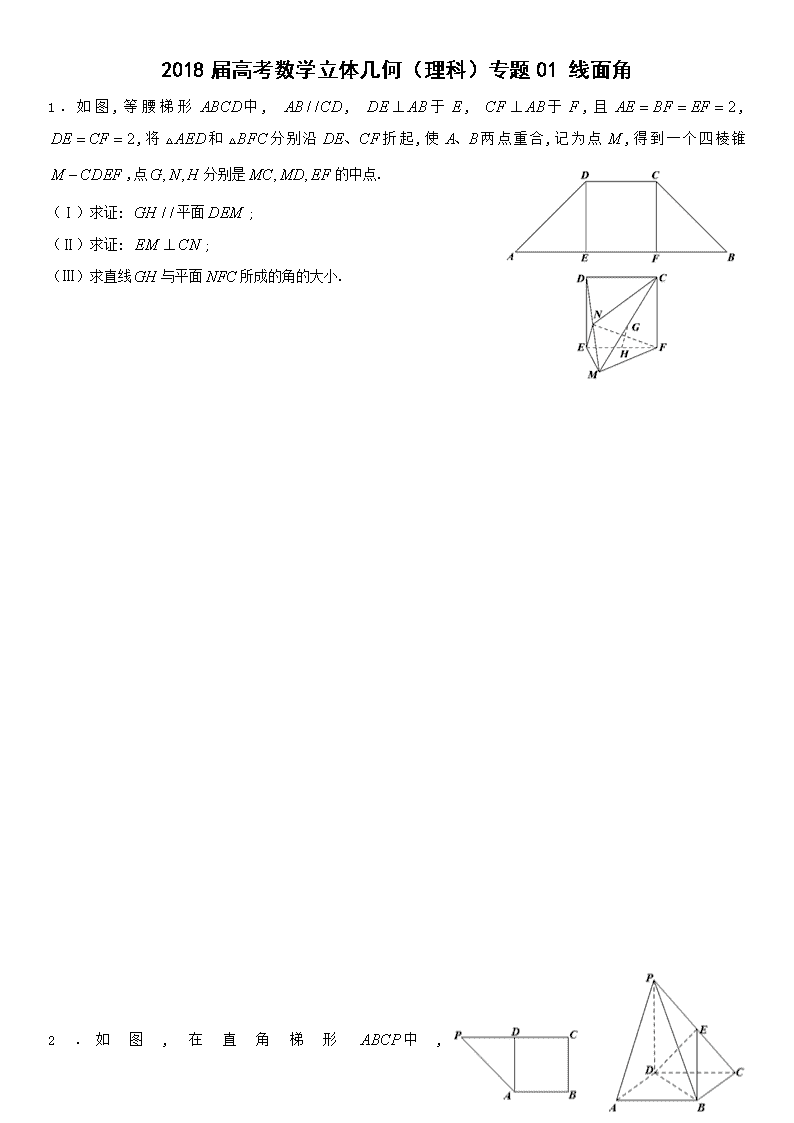
‎2018届高考数学立体几何（理科）专题01 线面角 ‎1．如图,等腰梯形中, , 于, 于,且, ,将和分别沿折起,使两点重合,记为点,得到一个四棱锥,点分别是的中点.‎ ‎（Ⅰ）求证: 平面;‎ ‎（Ⅱ）求证: ;‎ ‎（Ⅲ）求直线与平面所成的角的大小. ‎ ‎2．如图,在直角梯形中, ‎ ‎, 是的中点,将沿折起,使得.‎ ‎（Ⅰ）若是的中点,求证: 平面;‎ ‎（Ⅱ）求证:平面平面;‎ ‎（Ⅲ）求二面角的大小.‎ ‎3．如图，在矩形中， ， ， 是的中点，以为折痕将向上折起， ‎ 变为，且平面平面.‎ ‎（Ⅰ）求证： ；‎ ‎（Ⅱ）求二面角的大小.‎ ‎4．如图，在四棱锥PABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD＝CD＝2，BC＝4，PA＝2.‎ ‎(1)求证：AB⊥PC；‎ ‎(2)在线段PD上，是否存在一点M，使得二面角MACD的大小为45°，如果存在，求BM与平面MAC所成角的正弦值，如果不存在，请说明理由．‎ ‎5．如图1，在△中，，分别为，的中点，为的中点，‎ ‎，．将△沿折起到△的位置，使得平面平面，如图2．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求直线和平面所成角的正弦值；‎ ‎（Ⅲ）线段上是否存在点，使得直线和所成角的余弦值为？若存在，求出的值；若不存在，说明理由．‎ ‎6．‎ 已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形.‎ ‎（1）为中点，在线段上是否存在一点，使得平面？若存在，求出的长；若不存在，请说明理由；‎ ‎（2）求二面角的余弦值. ‎ ‎2018届高考数学立体几何（理科）专题01 线面角（教师版）‎ ‎1．如图,等腰梯形中, , 于, 于,且, ,将和分别沿折起,使两点重合,记为点,得到一个四棱锥,点分别是的中点.‎ ‎（Ⅰ）求证: 平面;‎ ‎（Ⅱ）求证: ;‎ ‎（Ⅲ）求直线与平面所成的角的大小.‎ ‎【答案】（1）见解析（2）见解析（3）‎ 试题解析：证明:（Ⅰ）连结,因为分别是的中点,所以,‎ 因为是的中点, , ,所以,所以,‎ 所以四边形是平行四边形,所以,‎ 又平面, 平面,所以平面.‎ 以为原点,以为坐标轴建立空间直角坐标系,‎ 则,所以,‎ 所以,所以.‎ 解:（Ⅲ）,‎ 所以,‎ 所以,所以直线与平面所成角的正弦值为,‎ 所以直线与平面所成角为.‎ ‎2．如图,在直角梯形中, , 是的中点,将沿折起,使得.‎ ‎（Ⅰ）若是的中点,求证: 平面;‎ ‎（Ⅱ）求证:平面平面;‎ ‎（Ⅲ）求二面角的大小.‎ ‎【答案】（1）见解析（2）见解析（3）‎ ‎（Ⅱ）由已知可得又因为平面所以平面 因为平面所以平面平面 解:（Ⅲ）由（Ⅱ）知, 平面所以,又因为所以平面 所以以为原点,以所在的直线分别为轴, 轴, 轴,建立如图所示的空间直角坐标系,‎ 则点, , , , .‎ 所以,,.设平面的法向量为,‎ 所以即令,解得.‎ 设平面的法向量为,所以即令,解得.‎ 所以.‎ 由图可知,二面角为钝角,所以二面角的大小为.‎ ‎3．如图，在矩形中， ， ， 是的中点，以为折痕将向上折起， 变为，且平面平面.‎ ‎（Ⅰ）求证： ；（Ⅱ）求二面角的大小.‎ ‎【答案】（Ⅰ）证明见解析；（Ⅱ） .‎ 试题解析：（Ⅰ）证明：∵， ，∴，∴， ‎ 取的中点，连结，则， ‎ ‎∵ 平面平面，∴平面，∴ ，从而平面，∴‎ ‎（Ⅱ）如图建立空间直角坐标系，‎ 设为平面的法向量，‎ 则可以取 因此， ，有，即平面 平面，故二面角的大小为.‎ ‎4．如图，在四棱锥PABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD＝CD＝2，BC＝4，PA＝2.(1)求证：AB⊥PC；‎ ‎(2)在线段PD上，是否存在一点M，使得二面角MACD的大小为45°，如果存在，求BM与平面MAC所成角的正弦值，如果不存在，请说明理由．‎ ‎【答案】（1）见解析（2）‎ ‎【解析】‎ 所以∠BAC＝90°，即AB⊥AC，因为PA⊥平面ABCD，所以PA⊥AB，又PA∩AC＝A，所以AB⊥平面PAC，所以AB⊥PC.‎ ‎(2)存在，理由如下：取BC的中点E，则AE⊥BC，以A为坐标原点，AE，AD，AP所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系，则A(0,0,0)，C(2，2，0)，‎ D(0，2，0)， P(0，0,2)，B(2，－2，0)，＝(0,2，－2)，＝(2，2，0)．‎ 设＝t (0＜t＜1)，则点M的坐标为(0,2t，2－2t)，所以＝(0,2t,2－2t)．‎ 设平面MAC的法向量是n＝(x，y，z)，‎ 则即令x＝1，得y＝－1，z＝，则n＝.‎ 又m＝(0,0,1)是平面ACD的一个法向量，所以|cos〈m，n〉|＝＝＝，‎ ‎5．如图1，在△中，，分别为，的中点，为的中点，，．将△沿折起到△的位置，使得平面平面，如图2．（Ⅰ）求证：；（Ⅱ）求直线和平面所成角的正弦值；‎ ‎（Ⅲ）线段上是否存在点，使得直线和所成角的余弦值为？若存在，求出的值；若不存在，说明理由．‎ ‎【答案】（Ⅰ）见解析．（Ⅱ）．（Ⅲ）．‎ ‎【解析】试题分析：第一问根据等腰三角形的特征，可以得出，再结合面面垂直的性质定理，可以得出平面，再根据线面垂直的性质，可以得出以 ，之后根据面面垂直的性质和线面垂直的性质得出结果；第二问根据题中的条件，建立空间直角坐标系，利用空间向量求得结果；第三问关于是否存在类问题，都是假设其存在，结合向量所成角的余弦值求得结果.‎ 所以 平面，所以 ．‎ ‎（Ⅱ）取的中点，连接，所以．由（Ⅰ）得，．‎ 如图建立空间直角坐标系．由题意得，，，，．‎ 所以，，．设平面的法向量为，‎ 则即令，则，，所以．‎ 设直线和平面所成的角为，则．‎ 所以 直线和平面所成角的正弦值为．‎ 所以．令，‎ 整理得．解得，舍去．所以 线段上存在点适合题意，且．‎ ‎6．已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形.（1）为中点，在线段上是否存在一点，使得平面？若存在，求出的长；若不存在，请说明理由；（2）求二面角的余弦值. ‎ ‎【答案】（1）存在；（2）.‎ ‎.‎ ‎（1）设平面的法向量，∵，∴，‎ ‎∴令，可解得平面的一个法向量，设，由于，则，又∵平面，∴，即，‎ ‎∴在线段上存在一点，使得平面，此时；‎ ‎∴令，可解得平面的一个法向量，∴.‎ 由图可知，所求二面角为锐角，即二面角余弦值为.‎