高考数学总复习73简单的线性规划问题但因为测试新人教B版 17页

‎2013年高考数学总复习 7-3 简单的线性规划问题但因为测试 新人教B版 ‎1.(文)(2010·北京东城区)在平面直角坐标系中，若点(－2，t)在直线x－2y＋4＝0的上方，则t的取值范围是(　　)‎ A．(－∞，1)　　 B．(1，＋∞)‎ C．(－1，＋∞) D．(0,1)‎ ‎[答案]　B ‎[解析]　∵点O(0,0)使x－2y＋4>0成立，且点O在直线下方，故点(－2，t)在直线x－2y＋4＝0的上方⇔－2－2t＋4<0，∴t>1.‎ ‎[点评]　可用B值判断法来求解，令d＝B(Ax0＋By0＋C)，则d>0⇔点P(x0，y0)在直线Ax＋By＋C＝0的上方；d<0⇔点P在直线下方．‎ 由题意－2(－2－2t＋4)>0，∴t>1.‎ ‎(理)(2010·惠州市模拟)若‎2m＋2n<4，则点(m，n)必在(　　)‎ A．直线x＋y－2＝0的左下方 B．直线x＋y－2＝0的右上方 C．直线x＋2y－2＝0的右上方 D．直线x＋2y－2＝0的左下方 ‎[答案]　A ‎[解析]　∵‎2m＋2n≥2，由条件‎2m＋2n<4知，‎ ‎2<4，∴m＋n<2，即m＋n－2<0，故选A.‎ ‎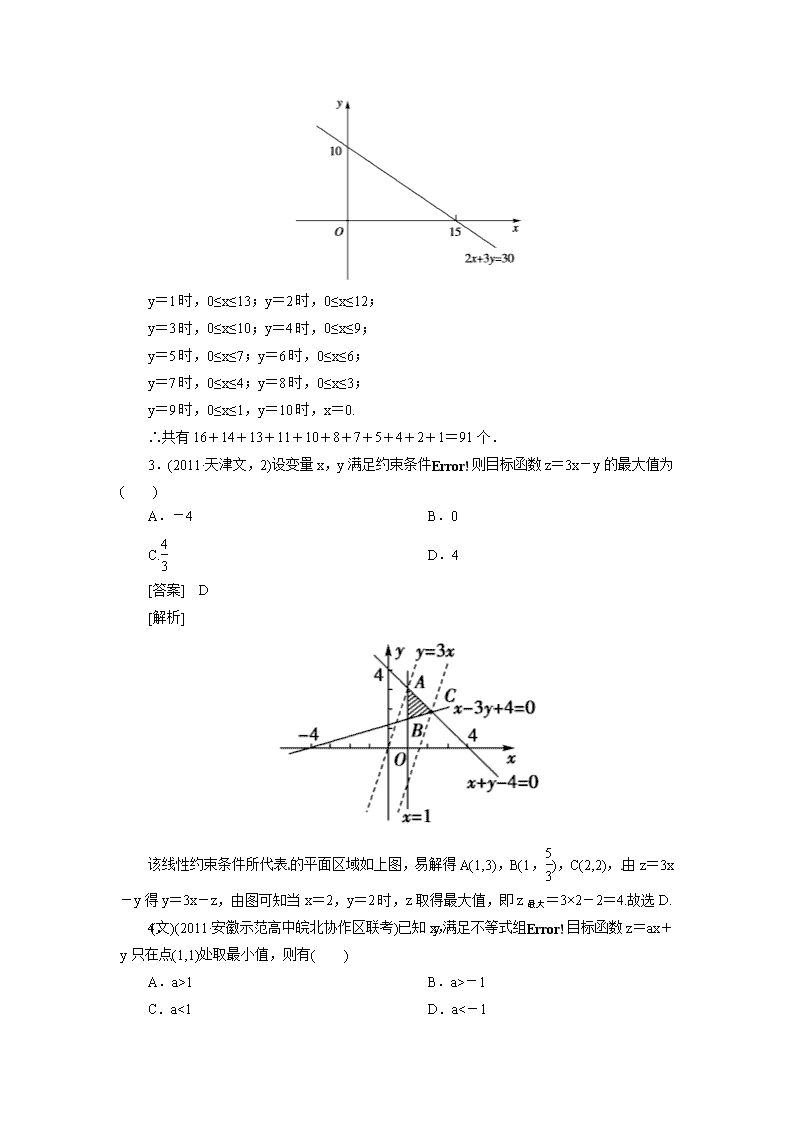2．(2010·四川广元市质检)在直角坐标系xOy中，已知△AOB的三边所在直线的方程分别为x＝0，y＝0,2x＋3y＝30，则△AOB内部和边上整点(即坐标均为整数的点)的总数为(　　)‎ A．95　 　 　 B．91　 　 　‎ C．88　 　 　 D．75‎ ‎[答案]　B ‎ ‎[解析]　由2x＋3y＝30知，y＝0时，0≤x≤15，有16个；‎ y＝1时，0≤x≤13；y＝2时，0≤x≤12；‎ y＝3时，0≤x≤10；y＝4时，0≤x≤9；‎ y＝5时，0≤x≤7；y＝6时，0≤x≤6；‎ y＝7时，0≤x≤4；y＝8时，0≤x≤3；‎ y＝9时，0≤x≤1，y＝10时，x＝0.‎ ‎∴共有16＋14＋13＋11＋10＋8＋7＋5＋4＋2＋1＝91个．‎ ‎3．(2011·天津文，2)设变量x，y满足约束条件则目标函数z＝3x－y的最大值为(　　)‎ A．－4 B．0 ‎ C. D．4‎ ‎[答案]　D ‎[解析]　‎ 该线性约束条件所代表的平面区域如上图，易解得A(1,3)，B(1，)，C(2,2)，由z＝3x－y得y＝3x－z，由图可知当x＝2，y＝2时，z取得最大值，即z最大＝3×2－2＝4.故选D.‎ ‎4．(文)(2011·安徽示范高中皖北协作区联考)已知x，y满足不等式组目标函数z＝ax＋y只在点(1,1)处取最小值，则有(　　)‎ A．a>1 B．a>－1‎ C．a<1 D．a<－1‎ ‎[答案]　D ‎[解析]　作出可行域如下图阴影部分所示．‎ 由z＝ax＋y，得y＝－ax＋z.‎ 只在点(1,1)处z取得最小值，则斜率－a>1，‎ 故a<－1，故选D.‎ ‎(理)(2011·宝鸡质检)已知约束条件，若目标函数z＝x＋ay(a≥0)恰好在点(2,2)处取得最大值，则a的取值范围为(　　)‎ A．0 D．0－3，∴a>.‎ ‎5．(2011·泉州质检)设不等式组所表示的平面区域为S，若A、B为区域S内的两个动点，则|AB|的最大值为(　　)‎ A．2 B. C．3 D. ‎ ‎[答案]　B ‎[解析]　在直角坐标平面内画出题中的不等式组表示的平面区域，结合下图观察不难得知，位于该平面区域内的两个动点中，‎ 其间的距离最远的两个点是(0,3)与(2,0)，因此|AB|的最大值是，选B.‎ ‎6．(2011·兰州模拟)设O为坐标原点，点M的坐标为(2,1)，若点N(x，y)满足不等式组，则使·取得最大值的点N的个数是(　　)‎ A．1 B．2 ‎ C．3 D．无数个 ‎[答案]　D ‎[分析]　点N(x，y)在不等式表示的平面区域之内，U＝·为x，y的一次表达式，则问题即是当点N在平面区域内变化时，求U取到最大值时，点N的个数．‎ ‎[解析]　如下图所示，可行域为图中阴影部分，而·＝2x＋y，所以目标函数为z＝2x＋y，作出直线l：2x＋y＝0，显然它与直线2x＋y－12＝0平行，平移直线l到直线2x＋y－12＝0的位置时目标函数取得最大值，故2x＋y－12＝0上每一点都能使目标函数取得最大值，故选D.‎ ‎7．如下图，若由不等式组(n>0)确定的平面区域的边界为三角形，且它的外接圆的圆心在x轴上，则实数m＝________.‎ ‎[答案]　－ ‎[解析]　根据题意，三角形的外接圆圆心在x轴上，‎ ‎∴OA为外接圆的直径，‎ ‎∴直线x＝my＋n与x－y＝0垂直，‎ ‎∴×＝－1，即m＝－.‎ ‎8．(2011·浏阳模拟)设变量x，y满足约束条件，则目标函数z＝4x＋y的最大值为________．‎ ‎[答案]　11‎ ‎[解析]　如下图，满足条件的可行域为三角形区域(图中阴影部分)，故z＝4x＋y在P(2,3)处取得最大值，最大值为11.‎ ‎9．铁矿石A和B的含铁率a，冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表：‎ a b(万吨)‎ c(百万元)‎ A ‎50%‎ ‎1‎ ‎3‎ B ‎70%‎ ‎0.5‎ ‎6‎ 某冶炼厂至少要生产1.9(万吨)铁，若要求CO2的排放量不超过2(万吨)，则购买铁矿石的最少费用为________(百万元)．‎ ‎[答案]　15‎ ‎[解析]　设需购买A矿石x万吨，B矿石y万吨，则根据题意得到约束条件为：‎ ，‎ 目标函数为z＝3x＋6y，当目标函数经过(1,2)点时目标函数取得最小值，最小值为：zmin＝3×1＋6×2＝15.‎ ‎10．(2011·福建厦门外国语学校月考)制订投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%.投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？‎ ‎[解析]　设投资人分别用x万元、y万元投资甲、乙两个项目，‎ 由题意知目标函数z＝x＋0.5y.‎ 上述不等式组表示的平面区域如下图所示，阴影部分(含边界)即可行域．‎ 作直线l0：x＋0.5y＝0，并作平行于直线l0的一组直线x＋0.5y＝z，z∈R，与可行域相交，其中有一条直线经过可行域上的M点，此时z取得最大值，这里M点是直线x＋y＝10和0.3x＋0.1y＝1.8的交点．‎ 解方程组得x＝4，y＝6.‎ 此时z＝1×4＋0.5×6＝7(万元)．‎ ‎∴当x＝4，y＝6时z取得最大值．‎ 答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大.‎ ‎11.(文)(2010·揭阳市模考、重庆南开中学模考)已知正数x、y满足，则z＝x·y的最小值为(　　)‎ A．1 B. ‎ C. D. ‎[答案]　C ‎[解析]　如下图易得2x＋y的最大值为4，从而z＝4－x·y＝2x＋y的最小值为，选C.‎ ‎(理)(2011·重庆一诊)设实数x，y满足条件，若目标函数z＝ax＋by(a>0，b>0)的最大值为12，则＋的最小值为(　　)‎ A. B. C. D．4‎ ‎[答案]　A ‎[解析]　如下图由可行域可得，当x＝4，y＝6时，目标函数z＝ax＋by取得最大值，∴‎4a＋6b＝12，即＋＝1，‎ ‎∴＋＝(＋)·(＋)＝＋＋≥＋2＝，故选A.‎ ‎12．(文)(2010·山师大附中模考)某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨，B原料2吨；生产每吨乙产品要用A原料1吨，B原料3‎ 吨，销售每吨甲产品可获得利润5万元，每吨乙产品可获得利润3万元．该企业在一个生产周期内消耗A原料不超过13吨，B原料不超过18吨．那么该企业可获得最大利润是(　　)‎ A．12万元 B．20万元 C．25万元 D．27万元 ‎[答案]　D ‎[解析]　设生产甲、乙两种产品分别为x吨，y吨，‎ 由题意得，‎ 获利润ω＝5x＋3y，画出可行域如下图，‎ 由，解得A(3,4)．‎ ‎∵－3<－<－，‎ ‎∴当直线5x＋3y＝ω经过A点时，ωmax＝27.‎ ‎(理)(2011·四川文，10)某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车，某天需送往A地至少72吨的货物，派用的每辆车需载满且只运送一次，派用的每辆甲型卡车需配2名工人，运送一次可得利润450元；派用的每辆乙型卡车需配1名工人；运送一次可得利润350元，该公司合理计划当天派用甲乙卡车的车辆数，可得最大利润z＝(　　)‎ A．4650元 B．4700元 C．4900元 D．5000元 ‎[答案]　C ‎[解析]　设该公司派甲型卡车x辆，乙型卡车y辆，由题意得 利润z＝450x＋350y，可行域如下图所示．‎ 解得A(7,5)．‎ 当直线350y＋450x＝z过A(7,5)时z取最大值，‎ ‎∴zmax＝450×7＋350×5＝4900(元)．故选C.‎ ‎13．(2011·广州一测)某校计划招聘男教师x名，女教师y名，x和y满足约束条件则该校招聘的教师最多是________名．‎ ‎[答案]　10‎ ‎[解析]　如下图在坐标平面内画出题中的不等式组表示的平面区域及直线x＋y＝0，平移该直线，因为x∈N，y∈N，所以当平移到经过该平面区域内的整点(5,5)时，相应直线在y轴上的截距最大，此时x＋y取得最大值，x＋y的最大值是10.‎ ‎14．(2011·苏北四市三调)在约束条件下，的最小值为________．‎ ‎[答案]　 ‎[解析]　在坐标平面内画出题中的不等式组表示的平面区域，注意到 可视为该区域内的点(x，y)与点(1,0)之间距离，结合下图可知，该距离的最小值等于点(1,0)到直线2y－x＝1的距离，即为＝.‎ ‎15．(文)(2010·吉林省质检)某单位投资生产A产品时，每生产1百吨需要资金2百万元，需场地2百平方米，可获利润3百万元；投资生产B产品时，每生产‎1百米需要资金3百万元，需场地1百平方米，可获利润2百万元．现该单位有可使用资金14百万元，场地9百平方米，如果利用这些资金和场地用来生产A、B两种产品，那么分别生产A、B两种产品各多少时，可获得最大利润？最大利润是多少？‎ ‎[解析]　设生产A产品x百吨，生产B产品y百米，共获得利润S百万元，则，‎ 目标函数为S＝3x＋2y.‎ 作出可行域如上图，‎ 由解得直线2x＋y＝9和2x＋3y＝14的交点为A，平移直线y＝－x＋，当它经过点A时，直线y＝－x＋在y轴上截距最大，S也最大．‎ 此时，S＝3×＋2×＝14.75.‎ 因此，生产A产品3.25百吨，生产B产品2.5百米，可获得最大利润，最大利润为1475万元．‎ ‎(理)(2010·茂名模考)某工厂生产甲、乙两种产品，每种产品都有一部分是一等品，其余是二等品，已知甲产品为一等品的概率比乙产品为一等品的概率多0.25，甲产品为二等品的概率比乙产品为一等品的概率少0.05.‎ ‎(1)分别求甲、乙产品为一等品的概率P甲，P乙；‎ ‎(2)已知生产一件产品需要用的工人数和资金数如表所示，且该厂有工人32名，可用资金55万元．设x，y分别表示生产甲、乙产品的数量，在(1)的条件下，求x，y为何值时，z＝xP甲＋yP乙最大，最大值是多少？‎ ‎　　　　　项目 用量　‎ 产品　　　　　‎ 工人(名)‎ 资金(万元)‎ 甲 ‎4‎ ‎20‎ 乙 ‎ ‎8‎ ‎5‎ ‎[解析]　(1)依题意得，‎ 解得，‎ 故甲产品为一等品的概率P甲＝0.65，乙产品为一等品的概率P乙＝0.4.‎ ‎(2)依题意得x、y应满足的约束条件为 ，且z＝0.65x＋0.4y.‎ 作出以上不等式组所表示的平面区域(如上图阴影部分)，即可行域．‎ 作直线l：0.65x＋0.4y＝0即13x＋8y＝0，把直线l向上方平移到l1的位置时，直线经过可行域内的点M，且l1与原点的距离最大，此时z取最大值．‎ 解方程组，得x＝2，y＝3.‎ 故M的坐标为(2,3)，所以z的最大值为zmax＝0.65×2＋0.4×3＝2.5‎ ‎1．在坐标平面上，不等式组所表示的平面区域的面积为(　　)‎ A. B. ‎ C. D．2‎ ‎[答案]　B ‎[解析]　不等式组的图形如下图．‎ 解得：A(0,1)　D(0，－1)　B(－1，－2)　C(，－)‎ S△ABC＝×|AD|×|xC－xB|＝×2×(＋1)‎ ‎＝，故选B.‎ ‎2．(2010·重庆市南开中学)不等式组所围成的平面区域的面积为(　　)‎ A．3 B．6 ‎ C．6 D．3‎ ‎[答案]　D ‎[解析]　不等式组表示的平面区域为图中Rt△ABC，易求B(4,4)，A(1,1)，C(2,0)‎ ‎∴S△ABC＝S△OBC－S△AOC＝×2×4－×2×1＝3.‎ ‎3．(2010·南昌市模拟)已知a，b∈R＋，a＋b＝1，M＝‎2a＋2b，则M的整数部分是(　　)‎ A．1 B．2 ‎ C．3 D．4‎ ‎[答案]　B ‎[解析]　∵a，b∈R＋，a＋b＝1，∴00，a≠1)的图象过区域M的a的取值范围是(　　)‎ A．[1,3] B．[2，]‎ C．[2,9] D．[，9]‎ ‎[答案]　C ‎[解析]　作出不等式表示的平面区域如下图，由得A(1,9)，由得B(3,8)，当函数y＝ax过点A时，a＝9，过点B时，a＝2，∴要使y＝ax的图象经过区域M，应有2≤a≤9.‎ ‎7．如下图，目标函数z＝ax－y的可行域为四边形OACB(含边界)，若C(，)是该目标函数z＝ax－y的最优解，则a的取值范围是________．‎ ‎[答案]　(－，－)‎ ‎8．某人有楼房一幢，室内面积共计‎180m2‎，拟分隔成两类房间作为旅游客房．大房间每间面积‎18m2‎，可住游客5名，每名游客每天住宿费40元；小房间每间面积‎15m2‎，可住游客3名，每名游客每天住宿费为50元；装修大房间每间需要1000元，装修小房间每间需要600元．如果他只能筹款8000元用于装修，且游客能住满客房，他隔出大房间和小房间各多少间，能获得最大收益？‎ ‎[解析]　设隔出大房间x间，小房间y间时收益为z元，‎ 则x，y满足，且z＝200x＋150y.‎ 约束条件可化简为：‎ 可行域为如下图所示的阴影部分(含边界)作直线l：200x＋150y＝0，即直线l：4x＋3y＝0把直线l向右上方平移至l1的位置时，直线经过点B，且与原点的距离最大，此时z＝200x＋150y取得最大值．‎ 解方程组，得到B(，)．‎ 由于点B的坐标不是整数，而最优解(x，y)中的x，y必须都是整数，所以，可行域内的点B(，)不是最优解，通过检验，当经过的整点是(0,12)和(3,8)时，z取最大值1800元．‎ 于是，隔出小房间12间，或大房间3间、小房间8间，可以获得最大收益．‎ ‎[点评]　当所求解问题的结果是整数，而最优解不是整数时，可取最优解附近的整点检验，找出符合题意的整数最优解．‎