高考冲刺样本07平面向量 21页

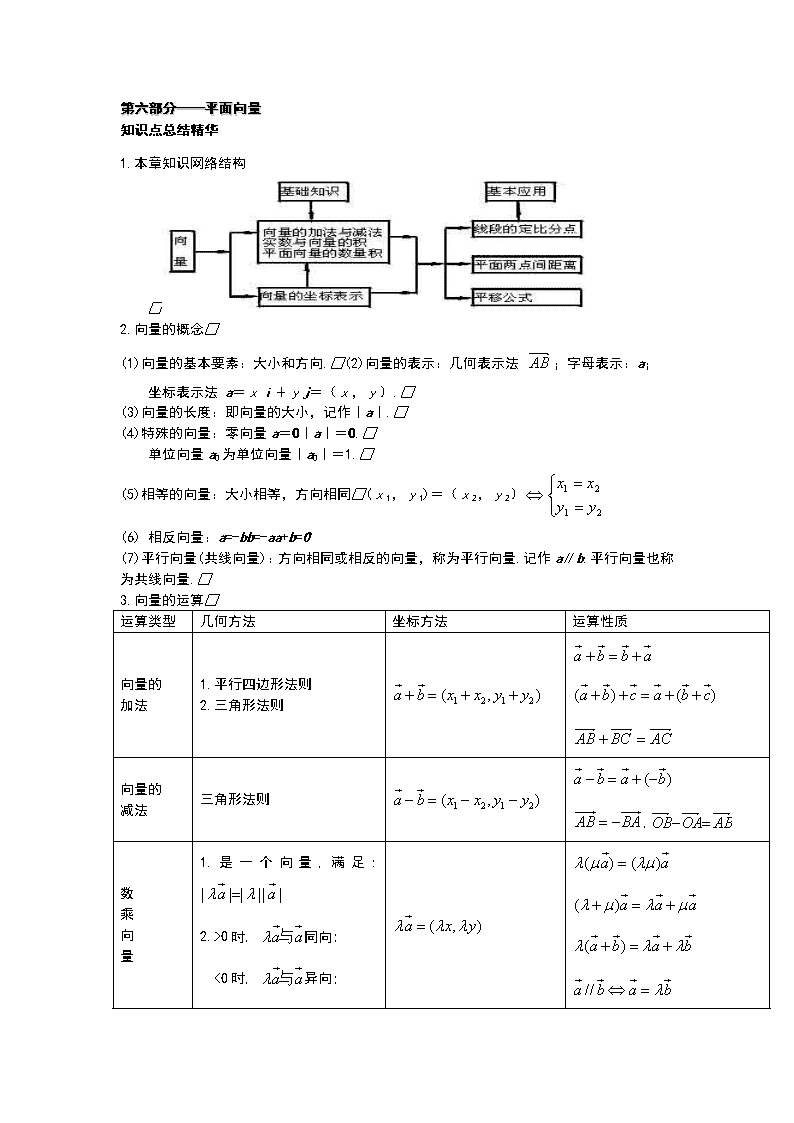
第六部分第六部分————平面向量平面向量 知识点总结精华 1.本章知识网络结构  2.向量的概念 (1)向量的基本要素：大小和方向.(2)向量的表示：几何表示法 ；字母表示：a； 坐标表示法 a＝ｘｉ＋ｙj＝（ｘ，ｙ）. (3)向量的长度：即向量的大小，记作｜a｜. (4)特殊的向量：零向量 a＝O｜a｜＝O. 单位向量 aO 为单位向量｜aO｜＝1. (5)相等的向量：大小相等，方向相同(ｘ1，ｙ1)＝（ｘ2，ｙ2） (6) 相反向量：a=-bb=-aa+b=0 (7)平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作 a∥b.平行向量也称 为共线向量. 3.向量的运算 运算类型 几何方法 坐标方法 运算性质 向量的 加法 1.平行四边形法则 2.三角形法则 向量的 减法 三角形法则 , 数 乘 向 量 1. 是 一 个 向 量 , 满 足 : 2.>0 时, 同向; <0 时, 异向; AB    = =⇔ 21 21 yy xx 1 2 1 2( , )a b x x y y+ = + +  a b b a+ = +    ( ) ( )a b c a b c+ + = + +      ACBCAB =+ 1 2 1 2( , )a b x x y y− = − −  ( )a b a b− = + −    AB BA= −  ABOAOB =− | | | || |a aλ λ=  a aλ 与 a aλ 与 ( , )a x yλ λ λ= ( ) ( )a aλ µ λµ=  ( )a a aλ µ λ µ+ = +   ( )a b a bλ λ λ+ = +    //a b a bλ⇔ =    =0 时, . 向 量 的 数 量 积 是一个数 1. 时， . 2. 4.重要定理、公式 (1)平面向量基本定理 e1，e2 是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一 对实数λ1， λ2，使 a＝λ1e1＋λ2e2. (2)两个向量平行的充要条件 a∥ba＝λb(b≠0)x1y2－x2y1＝O. (3)两个向量垂直的充要条件 a⊥ba·b＝Ox1x2＋y1y2＝O. (4)线段的定比分点公式 设点 P 分有向线段 所成的比为λ，即 ＝λ ，则 ＝ ＋ (线段的定比分点的向量公式) (线段定比分点的坐标公式) 当λ＝1 时，得中点公式： ＝ （ ＋ ）或 (5)平移公式 设点 P(x，y)按向量 a＝（ｈ，ｋ）平移后得到点 P′（x′，y′）， 0aλ =  a b•  0 0a b= =   或 0a b• =  0 0 | || | cos( , ) a b a b a b a b ≠ ≠ =          且 时， 1 2 1 2a b x x y y• = +  a b b a• = •    ( ) ( ) ( )a b a b a bλ λ λ• = • = •      ( )a b c a c b c+ • = • + •       2 2 2 2| | | |=a a a x y= +  即 | | | || |a b a b• ≤    21PP PP1 2PP OP λ+1 1 1OP λ+1 1 2OP       + += + += .1 ,1 21 21 λ λ λ λ yyy xxx OP 2 1 1OP 2OP      += += .2 ,2 21 21 yyy xxx 则 ＝ +a 或 曲线 y＝f（x）按向量 a＝（ｈ，ｋ）平移后所得的曲线的函数解析式为： y－ｋ＝f（x－ｈ) (6)正、余弦定理 正弦定理： 余弦定理：a2＝b2＋c2－2bccosA， b2＝c2＋a2－2cacosB， c2＝a2＋b2－2abcosC. （7）三角形面积计算公式： 设△ABC 的三边为 a，b，c，其高分别为 ha，hb，hc，半周长为 P，外接圆、内切圆的半径为 R，r. ①S△=1/2aha=1/2bhb=1/2chc②S△=Pr ③S△=abc/4R ④S△=1/2sinC·ab=1/2ac·sinB=1/2cb·sinA ⑤S△= [海伦公式] ⑥S△=1/2（b+c-a）ra[如下图]=1/2（b+a-c）rc=1/2（a+c-b）rb [注]：到三角形三边的距离相等的点有 4 个，一个是内心，其余 3 个是旁心. 如图： 图 1 中的 I 为 S△ABC 的内心， S△=Pr 图 2 中的 I 为 S△ABC 的一个旁心，S△=1/2（b+c-a）ra 附：三角形的五个“心”； 重心：三角形三条中线交点. 外心：三角形三边垂直平分线相交于一点. 内心：三角形三内角的平分线相交于一点. 垂心：三角形三边上的高相交于一点. 旁心：三角形一内角的平分线与另两条内角的外角平分线相交一点. ⑸已知⊙O 是△ABC 的内切圆，若 BC=a，AC=b，AB=c [注：s 为△ABC 的半周长,即 ] 则：①AE= =1/2（b+c-a） ②BN= =1/2（a+c-b） ③FC= =1/2（a+b-c） 综合上述：由已知得，一个角的邻边的切线长，等于半周长减去对边（如图 4）. 特例：已知在 Rt△ABC，c 为斜边，则内切圆半径 r= （如图 3）. ⑹在△ABC 中，有下列等式成立 . 证明：因为 所以 ，所以 ，结论！ ⑺在△ABC 中，D 是 BC 上任意一点，则 . 证明：在△ABCD 中，由余弦定理，有 ① PO ′ OP    +=′ +=′ . , kyy hxx .2sinsinsin RC c B b A a === ( )( )( )cPbPaPP −−− 2 cba ++ as − bs − cs − cba abcba ++=−+ 2 CBACBA tantantantantantan =++ ,CBA −=+ π ( ) ( )CBA −=+ πtantan CBA BA tantantan1 tantan −=− + DCBDBC BCABBDACAD ⋅−+= 22 2 BBDABBDABAD cos2222 ⋅⋅−+= A BC O a b c I A B C D E F I A B C D E F ra ra ra bc a a bc A C B N E F 在△ABC 中，由余弦定理有 ②，②代入①，化简 可得， （斯德瓦定理） ①若 AD 是 BC 上的中线， ； ②若 AD 是∠A 的平分线， ，其中为半周长； ③若 AD 是 BC 上的高， ，其中为半周长. ⑻△ABC 的判定： △ABC 为直角△∠A + ∠B = ＜ △ABC 为钝角△∠A + ∠B＜ ＞ △ABC 为锐角△∠A + ∠B＞ 附：证明： ，得在钝角△ABC 中， ⑼平行四边形对角线定理：对角线的平方和等于四边的平方和. 空间向量 1．空间向量的概念： 具有大小和方向的量叫做向量 注：⑴空间的一个平移就是一个向量 ⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑶空间的两个向量可用同一平面内的两条有向线段来表示 2．空间向量的运算 定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下 运算律：⑴加法交换律： ⑵加法结合律： ⑶数乘分配律： 3 共线向量 表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平 BCAB ACBCABB ⋅ −+= 2cos 222 DCBDBC BCABBDACAD ⋅−+= 22 2 222 222 1 acbma −+= ( )appbccbta −⋅+= 2 ( )( )( )cpbpappaha −−−= 2 ⇔+= 222 bac 2 π ⇔+ 22 ba 2 π ⇔+ 22 ba 2 π ab cbaC 2cos 222 −+= 222222 ,00cos cbacbaC  +⇔−+⇔ )(2 2222 bababa +=−++ baABOAOB  +=+= baOBOABA  −=−= )( RaOP ∈= λλ abba  +=+ )()( cbacba  ++=++ baba  λλλ +=+ )( D A CB Í ¼5 行向量．平行于记作 ． 当我们说向量、共线（或//）时，表示、的有向线段所在的直线可能是同一直线，也 可能是平行直线． 4．共线向量定理及其推论： 共线向量定理：空间任意两个向量、（≠），//的充要条件是存在实数λ，使＝λ. 推论：如果为经过已知点 A 且平行于已知非零向量的直线，那么对于任意一点 O，点 P 在直线上的充要条件是存在实数 t 满足等式 ． 其中向量叫做直线的方向向量. 5．向量与平面平行： 已知平面和向量，作 ，如果直线平行于或在内，那么我们说向量平行于平面， 记作： ． 通常我们把平行于同一平面的向量，叫做共面向量 说明：空间任意的两向量都是共面的 6．共面向量定理： 如果两个向量 不共线，与向量 共面的充要条件是存在实数 使 推 论 ： 空 间 一 点 位 于 平 面 内 的 充 分 必 要 条 件 是 存 在 有 序 实 数 对 ， 使 或对空间任一点，有 ① ①式叫做平面 的向量表达式 7 空间向量基本定理： 如果三个向量 不共面，那么对空间任一向量，存在一个唯一的有序实数组 ，使 推论：设 是不共面的四点，则对空间任一点，都存在唯一的三个 有序实数 ，使 8 空间向量的夹角及其表示： 已知两非零向量 ，在空间任取一点，作 ，则 叫做向量与的 夹角，记作 ；且规定 ，显然有 ；若 ， 则称与互相垂直，记作： . 9．向量的模： 设 ，则有向线段的长度叫做向量的长度或模，记作：. 10．向量的数量积： ． 已知向量 和轴，是上与同方向的单位向量，作点在上的射影，作点在上的射 ba  // tOAOP += OA a=  //a α ,a b ,a b ,x y p xa yb= +   MAB ,x y MP xMA yMB= +   OP OM xMA yMB= + +    MAB , ,a b c  , ,x y z p xa yb zc= + +   , , ,O A B C , ,x y z OP xOA yOB zOC= + +    ,a b ,OA a OB b= =   AOB∠ ,a b< > 0 ,a b π≤< >≤ , ,a b b a< >=< >   , 2a b π< >= a b⊥  OA a=  a b⋅ = | | | | cos ,a b a b⋅ ⋅ < >   AB a=  影，则 叫做向量 在轴上或在上的正射影. 可以证明 的长度 ． 11．空间向量数量积的性质： （1） ．（2） ．（3） ． 12．空间向量数量积运算律： （ 1 ） ． （ 2 ） （ 交 换 律 ） （ 3 ） （分配律）． 空间向量的坐标运算 一．知识回顾： （1）空间向量的坐标：空间直角坐标系的 x 轴是横轴（对应为横坐标），y 轴是纵轴（对 应为纵轴），z 轴是竖轴（对应为竖坐标）. ①令=(a1,a2,a3), ，则 ∥ (用到常用的向量模与向量之间的转化： ) ②空间两点的距离公式： . （2）法向量：若向量所在直线垂直于平面，则称这个向量垂直于平面，记作 ，如果 那么向量叫做平面的法向量. （3）用向量的常用方法： ①利用法向量求点到面的距离定理：如图，设 n 是平面的法向量，AB 是平面的一条射线， 其中 ，则点 B 到平面的距离为 . ②利用法向量求二面角的平面角定理：设 分别是二面角 中平面 的法向量， 则 所成的角就是所求二面角的平面角或其补角大小（ 方向相同，则为补角， 反方，则为其夹角）. ③证直线和平面平行定理：已知直线 平面， ，且 CDE 三点不共线， A B′ ′ AB A B′ ′ | | | | cos , | |A B AB a e a e′ ′ = < >= ⋅      | | cos ,a e a a e⋅ = < >     0a b a b⊥ ⇔ ⋅ =   2| |a a a= ⋅   ( ) ( ) ( )a b a b a bλ λ λ⋅ = ⋅ = ⋅     a b b a⋅ = ⋅   ( )a b c a b a c⋅ + = ⋅ + ⋅      ),,( 321 bbbb = ),,( 332211 babababa ±±±=+ ))(,,( 321 Raaaa ∈= λλλλλ 332211 babababa ++=⋅ )(,, 332211 Rbababab ∈===⇔ λλλλ 3 3 2 2 1 1 b a b a b a ==⇔ 0332211 =++⇔⊥ babababa 222 321 aaaaaa ++=⋅= aaaaaa ⋅=⇒⋅=2 2 3 2 2 2 1 2 3 2 2 2 1 332211 |||| ,cos bbbaaa bababa ba baba ++⋅++ ++= ⋅ ⋅>=<   2 12 2 12 2 12 )()()( zzyyxxd −+−+−= α⊥a α⊥a α∈A || || n nAB⋅ 21 , nn βα −−l βα, 21 , nn 21 , nn 21 , nn ≠⊄a α∈⋅∈⋅ DCaBA , 则 a∥的充要条件是存在有序实数对 使 .（常设 求解 若 存在即证毕，若 不存在，则直线 AB 与平面相交）. 内心是三条角平分线的交点，它到三边的距离相等。 外心是三条边垂直平分线的交点，它 到三个顶点的距离相等。 （是充要条件）重心是三条中线的交点，它到顶点的距离是它到 对边中点距离的 2 倍。 垂心是三条高的交点，它能构成很多直角三角形相似。 与三角形的“四心”有关的一些常见的重要的向量关系式有： ① 设 ，则向量 必平分∠BAC，该向量必通过△ABC 的内心; ② 设 ，则向量 必平分∠BAC 的邻补角 ③ 设 ，则向量 必垂直于边 BC，该向量必通过△ABC 的垂心 ④ △ABC 中 一定过 的中点，通过△ABC 的重心 ⑤ 点是△ABC 的外心 ⑥ 点是△ABC 的重心 ⑦ 点是△ABC 的垂心 ⑧ 点是△ABC 的内心 (其中 a、b、c 为△ABC 三边) µλ ⋅ CECDAB µλ += CECDAB µλ += µλ, µλ, µλ, α ▲ n B C A α β ▲ n2 n1 α C E D A B ( )+∞∈ ,0λ )( AC AC AB AB +λ ( )+∞∈ ,0λ )( AC AC AB AB −λ ( )+∞∈ ,0λ ) coscos ( CAC AC BAB AB +λ ACAB + BC 222 OCOBOA ==⇔ 0=++⇔ OCOBOA OAOCOCOBOBOA ⋅=⋅=⋅ 0=⋅+⋅+⋅⇔ OCcOBbOAa ⑨ △ABC 的外心、重心、垂心共线，即 ∥ ⑩ 设为△ABC 所在平面内任意一点，G 为△ABC 的重心，，I 为△ABC 的内心， 则有 并 且 重 心 G （ XA + XB + XC 3 ， YA + YB + YC 3 ） 内 心 I （ aXA + bXB + cXC a + b + c ， ayA + byB + cyC a + b + c ） 试题精粹 江苏省 2011 年高考数学联考试题 10 ． （ 江 苏 天 一 中 学 、 海 门 中 学 、 盐 城 中 学 2011 届 高 三 调 研 考 试 ） 在 中 ， ，是 内一点，且满足 ，则 =▲．（-3） 7．（江苏省 2010 届苏北四市第一次联考）在△ABC 中， 分别为三个内角 A，B，C 的 对边，设向量 ， ，若⊥，则角 A 的大小为▲ ． 10．（江苏省 2010 届苏北四市第一次联考）已知 ，其中 OG OH )(3 1 OCOBOAOG ++= cba OCcOBbOAaOI ++ ++= ABC∆ 2,4 == ACAB ABC∆ 02 =++ MCMBMA BCAM ⋅ cba ,, ),( accbm −−= ),( acbn += 3 π )2sin,2(),sin,1( 2 xbxa == ，若 ，则 的值等于▲．1 11、（南通市六所省重点高中联考试卷）在△ABC 中， ，D 是 BC 边上任意一点（D 与 B、C 不重合）， 且 ，则等于▲ 11. （苏北四市 2011 届高三第一次调研考试）在△ABC 中，点 M 满足 ， 若 ，则实数 m 的值为▲． 讲评建议：一种思维是对已知向量向目标向量分解，一种思维是理解已知向量条件的几何 意义，既点 M 是三角形 ABC 的重心，再结合，三角形向量的中线形式，此问题观察即可 解决，所以掌握相关结论，有了结论便利于联想。 6．（苏州市 2011 届高三调研测试）设 分别是 的斜边 上的两个三等分点， 已知 ,则 ▲. 【解析】 16 ． （ 淮 阴 中 学 、 姜 堰 中 学 、 前 黄 中 学 2011 届 第 一 次 联 考 ） （ 14 分 ） 已 知 向 量 , , （1）若为 中点， ，求．的值； （2）若 是直角三角形，求的值。 16．解：(1) ∵ （1 分） 而 ∴ ， （7 分） ( )0,x π∈ a b a b⋅ = ⋅    tan x π 6A∠ = 2 2| | | |AB AD BD DC= + ⋅    MA MB MC+ + = 0   AB AC mAM+ + = 0   ,E F Rt ABC BC 3, 6AB AC= = AE AF⋅ =  ( ) ( )AE AF AB BE AC CF⋅ = + ⋅ +      ( ) ( ) 2 2 2 2 1 1 3 3 1 1 9 3 2 2 6 3 10.3 9 AB BC AC BC AB AC BC BC AC AB BC    = + ⋅ −       = ⋅ − + ⋅ − = = + =            ( )3,1AB = ( )1,AC a= − a R∈ BC ( ),2AD m= ABC∆ ( )1 11,2 2 aAD AB AC + = + =    ( ),2AD m= 1 1 2 2 m a =  + = × 3 1 a m =  = FE CB A （2）①当 时， ∴ （9 分） ②当 时，∵ （10 分） ∴ ∴ （12 分） ③当 时， ，∴ 综上 或 （14 分） 16、（南通市六所省重点高中联考试卷）（本题满分 14 分）已知向量 ， ， ， 其中、、为 的内角. (Ⅰ)求角的大小； (Ⅱ)若 ， ， 成等差数列，且 ，求 的长. 解：(Ⅰ) ………………………(2 分) 对于 ， ………………………(4 分) 又 ， ………………………(7 分) (Ⅱ)由 ， 由正弦定理得 ………………………(9 分) ， 即 ……………………(12 分) 由余弦弦定理 ， ， …………………(14 分) 16．（无锡市 1 月期末调研）(本小题满分 14 分) 90A = ° ( )3 1 1 0a× − + = 3a = 90B = ° ( )4, 1BC AC AB a= − = − − ( ) ( )3 4 1 1 0a× − + − = 13a = 90C = ° ( ) ( )1 4 1 0a a− × − + − = a R∉ 3a = )sin,(sin BAm = )cos,(cos ABn = Cnm 2sin=⋅ ABC∆ Asin Csin Bsin 18)( =−⋅ ACABCA AB )sin(cossincossin BAABBAnm +=⋅+⋅=⋅ CBACCBAABC sin)sin(0,, =+∴<<−=+∆ ππ .sinCnm =⋅∴ Cnm 2sin=⋅ .3,2 1cos,sin2sin π===∴ CCCC BACBCA sinsinsin2,sin,sin,sin +=得成等差比数列 .2 bac += 18,18)( =⋅∴=−⋅ CBCAACABCA .36,18cos == abCab abbaCabbac 3)(cos2 2222 −+=−+= 36,3634 222 =×−=∴ ccc .6=∴c 已知△ABC 中， , , , ． （1）求 ； （2）设 ，且已知 ， ，求 sinx． 16．（1）由已知 ，即 ， ∵ ∴ ，………………………………………………………………2 分 ∵ ， ∴ ， ………………………………………………………3 分 在 Rt△BCD 中， , 又 , ∴ ， ………………………… 5 分 ∴ ． ………………………………………………………………… 6 分 （2）在△ABC 中， ， ∴ ． …………………………………………… 7 分 即 ， ， …………………………………… 9 分 而 ， …………………………………………………………10 分 则 ， ……………………………………………… 12 分 ∴ ，∴ ． …………………………………… 14 分 １．（无锡市 1 月期末调研）已知 ，点M 在直线 OC 上运动，当 取最小时，求点 M 的坐标． 1 ． 设 ，………………………………………………………………………… 2 分 ∴ ， …………………………………………………………… 3 分 ， ………………………………………………… …………4 分 ∴ ………………………………………6 分 | | 10AC = | | 5AD = DBAD 11 5= 0CD AB =   AB AC−  BAC θ∠ = 4cos( ) 5xθ + = 02 x π− < < DBAD 11 5= 11 5D B AD=  | 5,AD =｜ | | 11DB = 0CD AB =   C D A B⊥ 2 2 2BC BD CD= + 2 2 2CD AC AD= − 2 2 2 2 196BC BD AC AD= + − = | | | 14AB AC BC− = =   2 1cos =∠BAC 3 πθ = 4cos( ) cos( )3 5x x πθ + = + = 3sin( )3 5x π + = ± 0,2 6 3 3x x π π π π− < < − < + < 1 3sin( ) sin( ) sin2 6 3 3 2x π π π− = − < + < = 3sin( )3 5x π + = 3 4 3sin sin[( ) ]3 3 10x x π π −= + − = (1,0,2), (2,2,0), (0,1,2)OA OB OC= = =   MA MB⋅  ( , ,2 )OM OC oλ λ λ= =  (1, ,2 2 )MA MO OA λ λ= + = − −   (2,2 , 2 )MB MO OB λ λ= + = − −   22 (2 ) 2 (2 2 ) 5 6 2MA MB λ λ λ λ λ λ⋅ = − − − − = − +  ， …………………………………………………………………………8 分 ∴ 当 时 ， 最 小 ． 此 时 ． ………………………………………………10 分 16．（徐州市 12 月高三调研）(本小题满分 14 分) 设 的 三 个 内 角 所 对 的 边 分 别 为 ， 且 满 足 . （Ⅰ）求角的大小； （Ⅱ）若 ，试求 的最小值. 16 ． 解 ： （ Ⅰ ） 因 为 ， 所 以 ， 即 ，则 …………4 分 所以 ，即 ，所以 ………………8 分 （Ⅱ）因为 ，所以 ，即 …12 分 所以 = ，即 的最小值为………………14 分 试题精粹 江苏省 2010 年高考数学联考试题 一、填空题: 13．（江苏省南通市 2010 年高三二模）如图正六边形 ABCDEF 中，P 是△CDE 内(包括边界) 的动点，设 （α、β∈R），则α+β的取值范围是▲． 23 15( )5 5 λ= − + 3 5 λ = MA MB⋅  3 6(0, , )5 5M ABC∆ , ,A B C , ,a b c (2 ) 0a c BC BA cCA CB+ ⋅ + ⋅ =    2 3b = AB CB⋅  (2 ) 0a c BC BA cCA CB+ ⋅ + ⋅ =    (2 ) cos cos 0a c ac B cab C+ + = (2 )cos cos 0a c B b C+ + = (2sin sin )cos sin cos 0A C B B C+ + = 2sin cos sin( ) 0A B C B+ + = 1cos 2B = − 2 3B π= 2 2 2 22 cos 3b a c ac π= + − 2 212 3a c ac ac= + + ≥ 4ac ≤ AB CB⋅  2 1cos 23 2ac ac π = − ≥ − AB CB⋅  AP AB AFα β= +   1．（江苏省无锡市 2010 年普通高中高三质量调研）已知向量=（1，1）与向量=（， ） 垂直，则=。 解析：由与垂直得 12 ． （ 江 苏 省 无 锡 市 部 分 学 校 2010 年 4 月 联 考 试 卷 ） 已 知 是 的 内 心 ， 若 ，则 。 答案： 解析：此题用到平几中的角平分线定理，如不清楚此定理，较难做对。 13．（江苏省泰州市 2010 届高三联考试题）等腰直角三角形 中， ， ， 是 边上的高，为 的中点，点 分别为 边和 边上的点， 且 关于直线 对称，当 时， ______▲_______． 2.(江苏通州市 2010 年 3 月高三素质检测)已知向量和向量的夹角为， ，则向量 2 2x− 2 2 0 2x x x+ − = ⇒ = ABC∆ ,4,3,2 === ABBCAC ACyABxAI += =+ yx 3 2 ABC 90A∠ = ° 2AB = AD BC AD M N、 AB AC M N、 AD 1 2PM PN⋅ = −  AM MB = | | 2,| | 3a b= =  C A BM NP （第 13 题） 和向量的数量积 =▲。3 13．(江苏通州市 2010 年 3 月高三素质检测)如图，在等腰直角三角形 ABC 中，AC＝BC＝1， 点 M，N 分别是 AB，BC 的中点，点 P 是△ABC（包括边界）内任一点．则 的取值范 围为 ▲． 4． （2010 年 3 月苏、锡、常、镇四市高三教学情况调查一）已知两个单位向量,的夹角为 ，若向量 ， ，则 =▲． 0 4 ． （ 江 苏 省 盐 城 市 2010 年 高 三 第 二 次 调 研 考 试 ） 已 知 向 量 ，若 ，则实数=▲.-1 6、（江苏省连云港市 2010 届高三二模试题）已知 A（－3，0），B（0， 3），O 为坐标 原点，点 C 在第二象限，且∠AOC＝60°，OC→ ＝λOA→ ＋OB→ ，则实数λ的值是▲． 1 3 11．（江苏省苏南六校 2010 年高三年级联合调研考试）在 中，已知 D 是 AB 边上一 点，若 ， ，则 _____________． 3. （2010 年江苏省苏北四市高三年级第二次模拟考试）已知向量 ， ， 若∥，则实数等于▲. 12. （2010 年江苏省苏北四市高三年级第二次模拟考试）如图，在平面四边形 中， 若 ，则 ▲.5 9、（江苏省南京市 2010 年 3 月高三第二次模拟）若平面向量 a,b 满足｛a+b｝=1,a+b 平行 于 y 轴，a=(2,-1),则 b=。（-2，2）或（-2，0） 10．（江苏省洪泽中学 2010 年 4 月高三年级第三次月考试卷）已知 是平面上不共 线 三 点 ， 设 为 线 段 垂 直 平 分 线 上 任 意 一 点 ， 若 ， ， 则 的值为.12 二、解答题 15．（江苏省无锡市 2010 年普通高中高三质量调研）（本题满分 14 分） 如图，在△OAB 中，已知 P 为线段 AB 上的一点， （1）若 ，求，的值； （2）若 ， ， ，且与 的夹角为 60°时，求 的 a b⋅  AN MP⋅  3 3,4 4  −   120 1 22= +a e e 14=b e ⋅a b ( )0,1 , (1,3), ( , )OA OB OC m m= = =   //AB AC  ABC∆ DBAD 3 1= 1 2CD CA CBλ λ= +   =− 21 λλ 1 2 (6 , 2)=a ( 3 , )k= −b ABCD 3 , 2AC BD= = ( ) ( )+ ⋅ + =   AB DC AC BD , ,O A B AB | | 7OA = | | 5OB = ( )OP OA OB−    .OP x OA y OB= ⋅ + ⋅   BP PA=  3BP PA=  | | 4OA = | | 2OB = OB OP AB⋅  A 第 12 题 C D B 值。 解析： （1）∵ ， ∴ ，即 ， 3 分 ∴ ，即 ， 5 分 （2）∵ ， ∴ ，即 7 分 ∴ 8 分 ∴ ， 9 分 10 分 12 分 14 分 16．（江苏省苏南六校 2010 年高三年级联合调研考试）（本小题满分 14 分） 在平行四边形 中，设 ， ，已知 ， ，其中 ； （1）求 的值；（2）求 的值。 平面向量与解析几何解题方法 在高中数学新课程教材中，学生学习平面向量在前，学习解析几何在后，而且教材中二 者知识整合的不多，很多学生在学习中就“平面向量”解平面向量题，不会应用平面向量去 解决解析几何问题。用向量法解决解析几何问题思路清晰，过程简洁，有意想不到的神奇效 果。著名教育家布鲁纳说过：学习的最好刺激是对所学材料的兴趣，简单的重复将会引起学 生大脑疲劳，学习兴趣衰退。这充分揭示方法求变的重要性，如果我们能重视向量的教学， 必然能引导学生拓展思路，减轻负担。 一、知识整合 平面向量是高中数学的新增内容，也是新高考的一个亮点。 向量知识、向量观点在数 学、物理等学科的很多分支有着广泛的应用，它具有代数形式和几何形式的“双重身份”， 能融数形与一体，能与中学数学教学内容的的许多主干知识综合，形成知识交汇点。而在高 中数学体系中，解析几何占有着很重要的地位，有些问题用常规方法去解决往往运算比较繁 BP PA=  BO OP PO OA+ = +    2OP OB OA= +   1 1 2 2OP OA OB= +   1 2x = 1 2y = 3BP PA=  3 3BO OP PO OA+ = +    4 3OP OB OA= +   3 1 4 4OP OA OB= +   3 4x = 1 4y = 3 1( ) ( )4 4OP AB OA OB OB OA⋅ = + ⋅ −      1 3 1 4 4 2OB OB OA OA OA OB= ⋅ − ⋅ + ⋅      2 21 3 1 12 4 4 2 94 4 2 2 = × − × + × × × = − ABCD DAB α∠ = CAB β∠ = 22AB AD BC CD BD⋅ = ⋅ =    4 3cos( ) 7 γ α− = 5( , )3 6 π πγ ∈ cosγ sin( 2 )β γ+ A B C D 杂，不妨运用向量作形与数的转化，则会大大简化过程。 二、例题解析 例 1、椭圆 的焦点为 FF，点 P 为其上的动点，当∠FP F 为钝角时，点 P 横坐标的取值范围是___。 解：F1（－,0）F2（,0）,设 P（3cos,2sin） 为钝角 ∴ =9cos2－5＋4sin2=5 cos2－1<0 解得： ∴点 P 横坐标的取值范围是（ ） 点评：解决与角有关的一类问题，总可以从数量积入手。本题中把条件中的角为钝角 转化为向量的数量积为负值，通过坐标运算列出不等式，简洁明了。 例 2、已知定点 A(-1,0)和 B(1,0)，P 是圆(x-3)2+(y-4)2=4 上的一动点，求 的最大值和最小值。 分析：因为 O 为 AB 的中点，所以 故可利用向量把问题转化为求向量 的最值。 解：设已知圆的圆心为 C，由已知可得： 又由中点公式得 所以 = = = 又因为 点 P 在圆(x-3)2+(y-4)2=4 上, 所以 且 所以 即 故 149 22 =+ yx 21PFF∠ 1 2 5 3cos , 2sin ) ( 5 3cos , 2sin )PF PF θ θ θ θ⋅ = − − − ⋅ − −  （ 5 5cos5 5 <<− θ 5 53,5 53− 2 2PA PB+ 2 ,PA PB PO+ =   OP { 1,0}, {1,0}OA OB= − =  0, 1OA OB OA OB∴ + = ⋅ = −    2PA PB PO+ =   2 2 2( ) 2PA PB PA PB PA PB+ = + − ⋅      2(2 ) 2( ) ( )PO OA OP OB OP− − ⋅ −     2 2 4 2 2 2 ( )PO OA OB OP OP OA OB− ⋅ − + ⋅ +       2 2 2OP + {3,4}OC = 5, 2,OC CP= =  OP OC CP= +   OC CP OP OC CP OC CP− ≤ = + ≤ +       3 7OP≤ ≤ 2 2 2 20 2 2 100PA PB OP≤ + = + ≤   P C y xA o B 所以 的最大值为 100，最小值为 20。 点评：有些解几问题虽然没有直接用向量作为已知条件出现，但如果运用向量知识来解 决，也会显得自然、简便，而且易入手。 例 3 、 O 是 平 面 上 一 定 点 ， A 、 B 、 C 是 平 面 上 不 共 线 的 三 个 点 ， 动 点 P 满 足 ， ，则 P 的轨迹一定通过△ABC 的（ ） （A）外心 （B）内心 （C）重心 （D）垂心 分析：因为 同向的单位向量，由向量加法的平行四边 形 则 知 是 与 ∠ ABC 的 角 平 分 线 （ 射 线 ） 同 向 的 一 个 向 量 ， 又 ，知 P 点的轨迹是∠ABC 的角平分线，从而点 P 的轨迹一 定通过△ABC 的内心。 反思：根据本题的结论，我们不难得到求一个角的平分线所在的直线方程的步骤； （1） 由顶点坐标（含线段端点）或直线方程求得角两边的方向向量 ； （2） 求出角平分线的方向向量 （3） 由点斜式或点向式得出角平分线方程。{直线的点向式方程：过 P（ ）， 其方向向量为 ，其方程为 } 例 4、（2003 年天津）已知常数 ，向量 ，经过原点以 为 方向向量的直线与经过定点 以 为方向向量的直线相交于点，其中 ．试 问：是否存在两个定点 ，使得 为定值，若存在，求出 的坐标；若不 存在，说明理由． （本小题主要考查平面向量的概念和计算,求轨迹的方法，椭圆的方程和性质，利用方 程判定曲线的性质，曲线与方程的关系等解析几何的基本思想和综合解题能力.） 解：根据题设条件，首先求出点 P 坐标满足的方程，据此再判断是否存在两定点，使得 点 P 到两定点距离的和为定值. ∵ ， ∴ =（λ，a）， =（1，－2λa）. 因此，直线 OP 和 AP 的方程分别为 和 . 2 2PA PB+ ) |||| ( AC AC AB ABOAOP ++= λ [ )∞∈ ＋，0λ | | | | AB AC AB AC AB AC      、 分别是与 、 | | | | AB AC AB AC +     ( )AB ACOP OA AP AB AC λ− = = +       1 2v v 、 1 2 1 2 v vv v v = +     0 0,x y ( , )v a b 0 0x x y y a b − −= 0>a (0, ) (1,0)c a= = ，i c iλ+  ),0( aA 2i cλ−  R∈λ FE、 PE PF+  FE、 (0, ) (1,0)c a= = ，i c iλ+  2i cλ−  axy =λ axay λ2−=− 消去参数λ，得点 的坐标满足方程 . 整理得 ……① 因为 所以得： （i）当 时，方程①是圆方程，故不存在合乎题意的定点 E 和 F； （ii）当 时，方程①表示椭圆，焦点 和 为合乎 题意的两个定点； （iii）当 时，方程①也表示椭圆，焦点 和 为合乎题意的两个定点. 点评：本题以平面向量为载体，考查求轨迹的方法、利用方程判定曲线的性质、曲线与 方程的关系等解析几何的基本思想和综合解题能力。去掉平面向量的背景，我们不难看到， 本题即为下题：在△OAP 中，O（0，0）、A（0，a）为两个定点，另两边 OP 与 AP 的斜率分 别是 ，求 P 的轨迹。 例 5．椭圆的中心是原点 O，它的短轴长为 ，相应于焦点 F（c，0）（ ）的准 线与 x 轴相交于点 A，|OF|=2|FA|，过点 A 的直线与椭圆相交于 P、Q 两点. （1）求椭圆的方程及离心率； （2）若 ，求直线 PQ 的方程； （3）设 （ ），过点 P 且平行于准线的直线与椭圆相交于另一点 M， 证明 . 分析：本小题主要考查椭圆的标准方程和几何性质，直线方程，平面向量的计算，曲线 和方程的关系等解析几何的基本思想方法和综合解题能力. （1）解：由题意，可设椭圆的方程为 . 由已知得 解得 所以椭圆的方程为 ，离心率 . （2）解：由（1）可得 A（3，0）. 设直线 PQ 的方程为 .由方程组 ),( yxP 222)( xaayy −=− .1 )2( )2( 8 1 2 2 2 = − + a ayx ,0>a 2 2=a 2 20 << a )2,2 1 2 1( 2 aaE − )2,2 1 2 1( 2 aaF −− 2 2>a ))2 1(2 1,0( 2 −+ aaE ))2 1(2 1,0( 2 −− aaF ( 0), 2a aλ λλ ≠ − 22 0>c 0=⋅OQOP AQAP λ= 1>λ FQFM λ−= )2(12 2 2 2 >=+ ay a x    −= =− ).(2 ,2 2 22 cc ac ca 2,6 == ca 126 22 =+ yx 3 6=e )3( −= xky 得 依题意 ，得 . 设 ，则 ， ① . ② 由直线 PQ 的方程得 .于是 . ③ ∵ ，∴ . ④ 由①②③④得 ，从而 . 所以直线 PQ 的方程为 或 （2）证明： .由已知得方程组 注意 ，解得 因 ，故 . 而 ，所以 . 三、总结提炼 由于向量具有几何形式和代数形式的“双重身份”，使向量与解析几何之间有着密切联 系，而新课程高考则突出了对向量与解析几何结合考查，这就要求我们在平时的解析几何教 学与复习中，应抓住时机，有效地渗透向量有关知识，树立应用向量的意识。应充分挖掘课 本素材，在教学中从推导有关公式、定理，例题讲解入手，让学生去品位、去领悟，在公式、 定理的探索、形成中逐渐体会向量的工具性，逐渐形成应用向量的意识，在教学中还应注重 引导学生善于运用一些问题的结论，加以引申，使之成为解题方法，体会向量解题的优越性，    −= =+ )3( ,126 22 xky yx 062718)13( 2222 =−+−+ kxkxk 0)32(12 2 >−=∆ k 3 6 3 6 <<− k ),(),,( 2211 yxQyxP 13 18 2 2 21 +=+ k kxx 13 627 2 2 21 + −= k kxx )3(),3( 2211 −=−= xkyxky ]9)(3[)3)(3( 2121 2 21 2 21 ++−=−−= xxxxkxxkyy 0=⋅OQOP 02121 =+ yyxx 15 2 =k )3 6,3 6(5 5 −∈±=k 035 =−− yx 035 =−+ yx ),3(),,3( 2211 yxAQyxAP −=−=          =+ =+ = −=− .126 ,126 , ),3(3 2 2 2 2 2 1 2 1 21 21 yx yx yy xx λ λ 1>λ λ λ 2 15 2 −=x ),(),0,2( 11 yxMF − ),1)3((),2( 1211 yxyxFM −+−=−−= λ ),2 1(),2 1( 21 yy λ λλλ −−=−−= ),2 1(),2( 222 yyxFQ λ λ −=−= FQFM λ−= 在教学中还应注重引导学生善于运用向量方法解题，逐步树立运用向量知识解题的意识。 向量与复数单元测试 1．设 a 是实数，且 是实数，则 2.设点 ， ,若点在直线 上，且 .则点的坐标为 3.已知向量 ， ，且 ，则 x 为_____________ 4.已知向量 ，若 与垂直，则 5.若向量 的夹角为 ， ，则 . 6.复数 等于 7. 向量 ， ，若 与 平行，则等于 8.与向量 ， 夹角相等的单位向量的坐标 9.如图，在 中， 是边上一点， 则 . 10.设 ，已知两个向量 ， ，则向量 长度的最大值是 11.如图，在 中，点是 的中点，过点的直线分别交直线 ， 于不同的两点 ，若 ， ，则 的值为 12.虚数（x－2）+ yi 其中 x、y 均为实数，当此虚数的模为 1 时， 的取值范围是 13、 已知 ,⑴ 设 .⑵ 如果 求实数 的值. 14、已知 , ,当为何值时， （1） 与 垂直？ （2） 与 平行？平行时它们是同向还是反 向？ 15.已知 之间有关系 ，其 中 k＞0, （1）用 k 表示 ；②求 的最小值，并求此时 夹角的大小。 参考答案 1、1 2、 或 3、4 4、2 5、2 6、 7、 1 1 2 a i i +++ (2,0)A (4,2)B AB AB = 2 AP (2,3)=a ( ,6)x=b //a b (1 ) ( 1 )n n= = −， ， ，a b 2 −a b =a 、a b 150 3, 4= =a b 2 + =a b 10(1 ) 1 i i + − (2,3)=a ( 1,2)= −b +ma b 2−a b (1,2)=a (2,1)=b ABC∆ 120 , 2, 1,BAC AB AC D∠ = ° = = 2 ,DC BD= AD BC =   πθ 20 <≤ ( )θθ sin,cos1 =OP ( )θθ cos2,sin22 −+=OP 21PP ABC△ BC AB AC M N， AB mAM=  AC nAN=  m n+ y x 1z i= + 2 3 4,z z iω ω= + − +求 2 2 11 z az b iz z + + = −− + a b、 (1,2)=a ( 3,2)= −b k +a b 3−a b k +a b 3−a b ( ) ( )cos ,sin , cos ,sin ,α α β β= =a b 与a b 3k + = −a b a kb ⋅a b ⋅a b 与a b (3,1) (1, 1)− ( )6 1i − 1 2 − 11 题 B A CD 第 9 题 8、 9、 10、 11、2 12、 13、解:⑴∵ , ∴ . ⑵ 由已知得 . 14、解： （1） ， 得 （2） ，得 此时 ，所以方向相反 15、解：①:∵ ∴ 即 ∴ ∵ ，所以 ∴ ②: ∵ ,∴ ∴ 的最小值为 又∵ ∴ ∴ 2 2 2 2( , ) ( , )2 2 2 2 − −或 8 3 − 23 3 30 03 3    − ∪       ， ， 2 3 3 4 1i i iω = + − − = − − 1 1i i iω + = − − + = 2 2 2 ( ) ( 2) ( 2) ( )2 1 11 z az b i a ai b a b a i a a b ii i iz z + + + + + + + += = = + − +− − +− + 2 1 1 ( ) 1 2 a a a b b + = = − ⇒ − + = − =  (1,2) ( 3,2) ( 3,2 2)k k k k+ = + − = − +a b 3 (1,2) 3( 3,2) (10, 4)− = − − = −a b ( )k + ⊥a b ( 3 )−a b ( )k + •a b ( 3 )−a b 10( 3) 4(2 2) 2 38 0, 19k k k k= − − + = − = = ( ) //k +a b ( 3 )−a b 14( 3) 10(2 2), 3k k k− − = + = − ( )k +a b 10 4 1( , ) (10, 4)3 3 3 = − = − − bkabak −=+ 3 ( )22 3ka b a kb+ = −    ( )2 2 2 22 22 3 2ka b ka bk ka b a b+ + ⋅ = − ⋅+       ( ) ( )2 22 23 3 1 8 k ka b a b k − + − ⋅ =     ( ) ( ),sin,cos,sin,cos ββαα == ba 1,1 22 == ba 2 1 4 ka b k +⋅ =  kk 212 ≥+ 2 1 4 2 4 12 =≥+ k k k k ba ⋅ 2 1 1,cos ==⋅⋅=⋅ bababa γ 2 1cos =γ 60=γ