高考数学套用个规范答题模板 32页

模板一　求函数值 ‎　例1【2018年理数全国卷II】已知是定义域为的奇函数，满足．若，则 ‎ A. B. 0 C. 2 D. 50‎ ‎【答案】C ‎【解析】‎ ‎▲模板构建　已知函数解析式求函数值,常伴随对函数的单调性、奇偶性、周期性和对称性的考查,其解题思路如下:‎ ‎【变式训练】【2018年江苏卷】函数满足，且在区间上， 则的值为________．‎ 模板二　函数的图象 ‎　例2【2018年理数全国卷II】函数的图像大致为 A. A B. B C. C D. 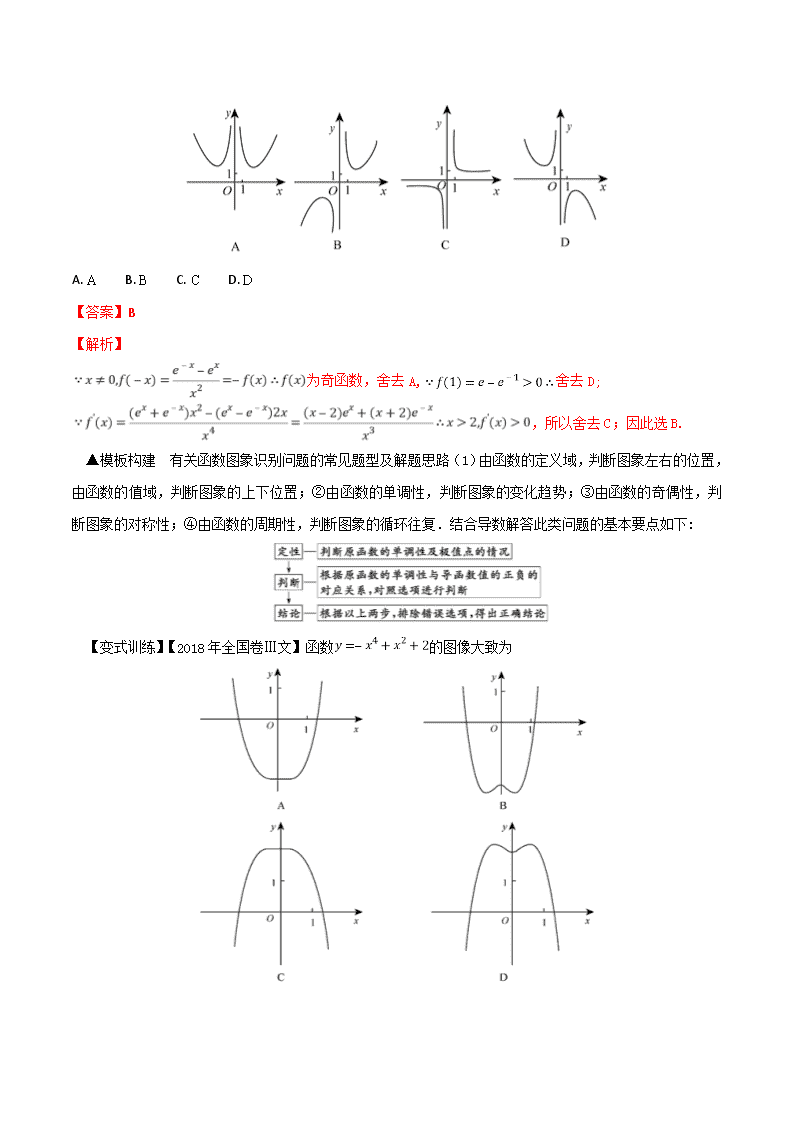D ‎【答案】B ‎【解析】‎ 为奇函数，舍去A,舍去D;‎ ‎，所以舍去C；因此选B.‎ ‎　▲模板构建　有关函数图象识别问题的常见题型及解题思路（1）由函数的定义域，判断图象左右的位置，由函数的值域，判断图象的上下位置；②由函数的单调性，判断图象的变化趋势；③由函数的奇偶性，判断图象的对称性；④由函数的周期性，判断图象的循环往复．结合导数解答此类问题的基本要点如下:‎ ‎　【变式训练】【2018年全国卷Ⅲ文】函数的图像大致为 模板三　函数的零点问题 ‎　例3 【2018届北京市十一学校3月零模】已知函数那么在下列区间中含有函数零点的是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎▲模板构建　利用零点存在性定理可以根据函数y=f(x)在某个区间端点处函数值的符号来确定零点所在区间.这种方法适用于不需要确定零点的具体值,只需确定其大致范围的问题.基本的解题要点为:‎ ‎【变式训练】【2018年江苏卷】若函数在内有且只有一个零点，则在上的最大值与最小值的和为________．‎ 模板四　三角函数的性质 ‎　例4【2018届福建省漳州市5月测试】已知函数（，），满足，且对任意，都有．当取最小值时，函数的单调递减区间为（ ）‎ A. ，Z B. ，Z C. ，Z D. ，Z ‎【答案】A ‎【解析】‎ 那么，函数，‎ 当时，取得最小值，‎ ‎，，‎ 即函数，‎ 令，‎ 得，‎ 所以，函数的单调递减区间为：‎ ‎，,故选A.‎ ‎▲模板构建　在利用三角函数的性质求最值或值域时,要注意:(1)先确定函数的定义域;(2)将已知函数化简为y=Asin(ωx+φ)+k的形式时,尽量化成A>0,ω>0的情况;(3)将ωx+φ视为一个整体.解题思路为:‎ ‎【变式训练】【2018辽宁省凌源市模拟】已知函数，当时，函数的最小值与最大值之和为__________．‎ 模板五　三角函数的图象变换 ‎　例5.将函数的图象上各点的横坐标缩小为原来的，再向右平移φ(φ>0)个单位后得到的图象关于直线对称，则φ的最小值是(　　)‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎▲模板构建　三角函数图象变换的主要类型:在x轴方向上的左、右平移变换,在y轴方向上的上、下平移变换,在x轴或y轴方向上的伸缩变换.其基本步骤如下:‎ ‎【变式训练】【2018湖南省长郡中学模拟】为了得到函数的图象，只需把函数的图象（ ）‎ A. 向左平移个单位长度 B. 向右平移个单位长度 C. 向左平移个单位长度 D. 向右平移个单位长度 模板六　解三角形 例6【2018年理数全国卷II】在中，，，，则 A. B. C. D. ‎ ‎【答案】A ‎▲模板构建　利用正弦定理、余弦定理都可以进行三角形的边、角之间的互化,当已知三角形的两边及一边的对角,或已知两角及一角的对边时,可以利用正弦定理求解三角形中的有关量;如果已知三边或两边及其夹角,则可利用余弦定理进行求解.其基本思路如下:‎ ‎【变式训练】‎ ‎【2018河南省南阳市第一中学模拟】在中，内角所对的边分别为.‎ ‎（1）求；‎ ‎（2）若的面积为，求的周长.‎ 模板七　利用函数性质解不等式 例7已知定义在上的偶函数在上递减且，则不等式的解集为__________．‎ ‎【答案】‎ ‎▲模板构建　函数性质法主要适用于解决抽象函数对应的不等式问题.其解题要点如下:‎ ‎【变式训练】【2018届广东省模拟（二）】已知函数，当时，关于的不等式的解集为__________．‎ 模板八　利用基本不等式求最值 例8．【2018广西钦州质量检测】已知（，为正实数），则的最小值为__________．‎ ‎【答案】‎ ‎【解析】∵a，b∈R+，a+4b=1‎ ‎∴=≥，‎ 当且仅当，即a=2b时上述等号成立，‎ 故答案为：9‎ ‎▲模板构建　拼凑法就是将函数解析式进行适当的变形,通过添项、拆项等方法凑成和为定值或积为定值的形式,然后利用基本不等式求最值.应用此法求最值的基本思路如下:‎ ‎【变式训练】已知,且满足,那么的最小值为____.‎ 模板九　不等式恒成立问题 例9【2018年天津卷文】已知a∈R，函数若对任意x∈［–3，+），f(x)≤恒成立，则a的取值范围是__________．‎ ‎【答案】［，2］‎ ‎【解析】‎ ‎▲模板构建　分离参数法是求解不等式恒成立问题的常用方法,其解题要点如下:‎ ‎【变式训练】【2018河南省中原名校联考】已知函数，当时， 恒成立，则实数的取值范围为（ ）‎ A. B. C. D. ‎ 模板十　简单的线性规划问题 ‎　例10【2018年理北京卷】若