人民教育出版版高考数学选修4124弦切角的性质基础训练 4页

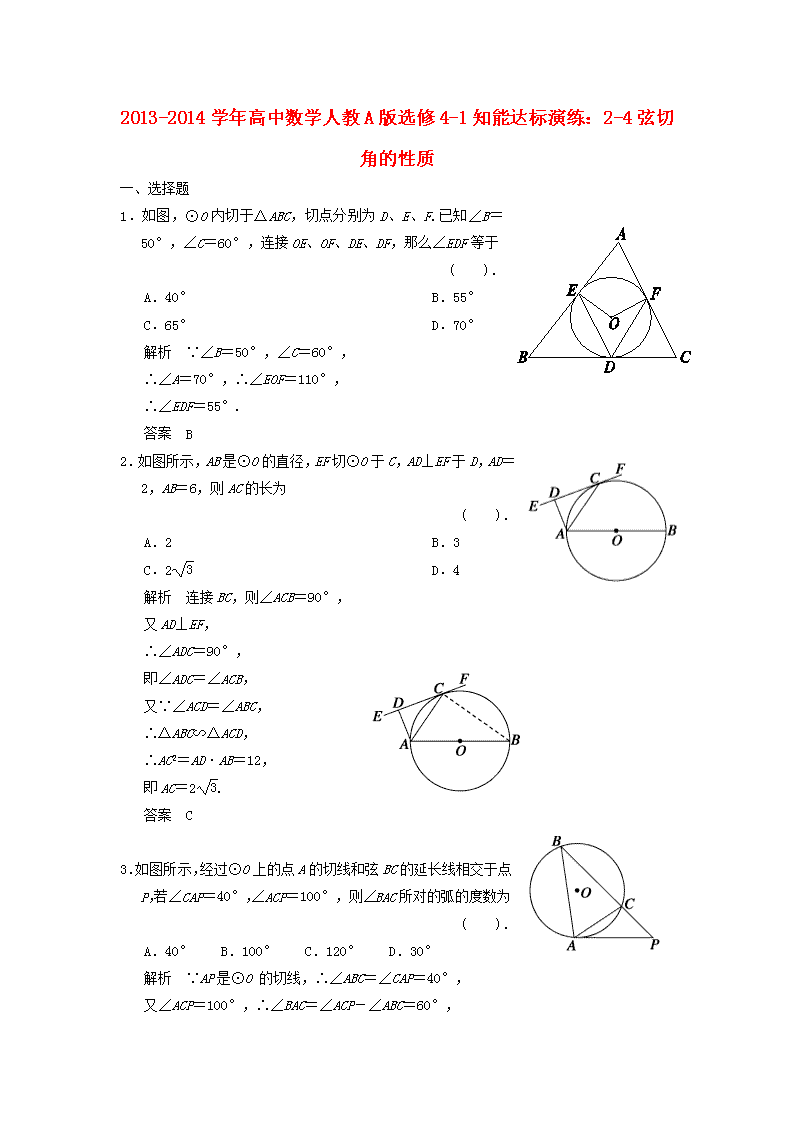
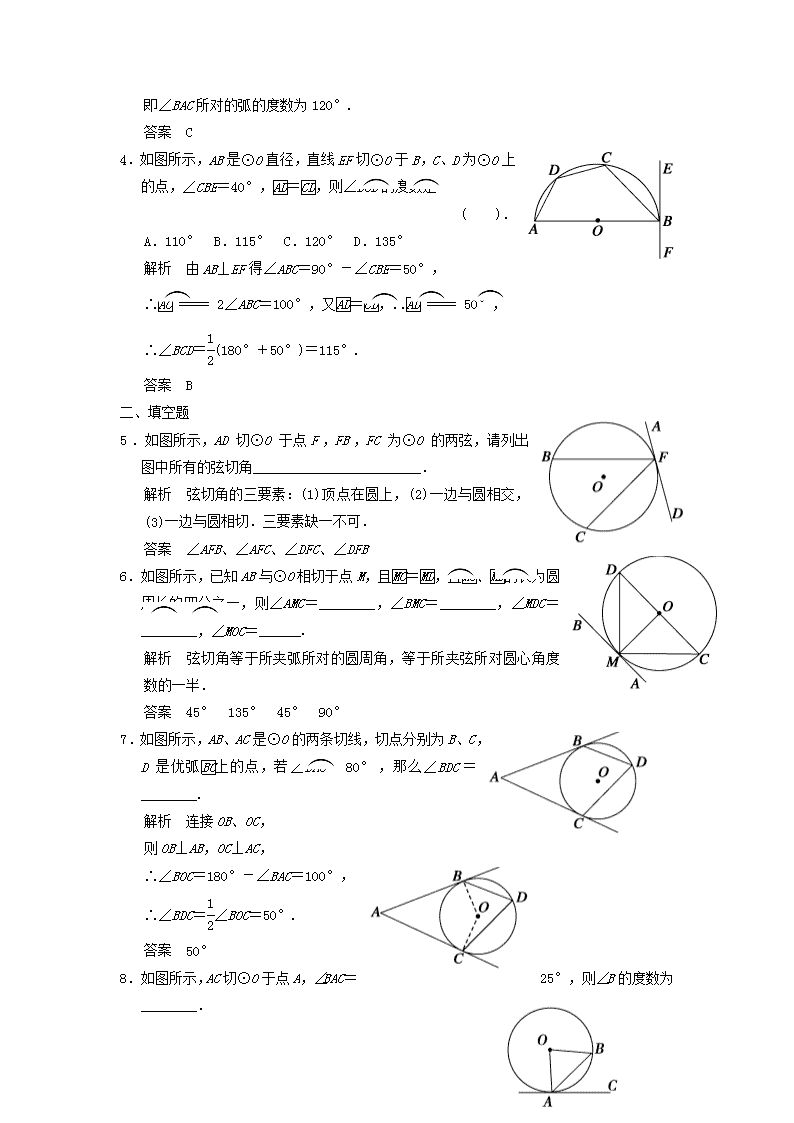
‎2013-2014学年高中数学人教A版选修4-1知能达标演练：2-4弦切角的性质 一、选择题 ‎1．如图，⊙O内切于△ABC，切点分别为D、E、F.已知∠B＝50°，∠C＝60°，连接OE、OF、DE、DF，那么∠EDF等于 ‎(　　)．　　　　　　　　　　　　　　　　　　‎ A．40°　　　　　　　　　 B．55°‎ C．65°　　　　　　　　　 D．70°‎ 解析　∵∠B＝50°，∠C＝60°，‎ ‎∴∠A＝70°，∴∠EOF＝110°，‎ ‎∴∠EDF＝55°.‎ 答案　B ‎2．如图所示，AB是⊙O的直径，EF切⊙O于C，AD⊥EF于D，AD＝2，AB＝6，则AC的长为 ‎(　　)．‎ A．2 B．3‎ C．2 D．4‎ 解析　连接BC，则∠ACB＝90°，‎ 又AD⊥EF，‎ ‎∴∠ADC＝90°，‎ 即∠ADC＝∠ACB，‎ 又∵∠ACD＝∠ABC，‎ ‎∴△ABC∽△ACD，‎ ‎∴AC2＝AD·AB＝12，‎ 即AC＝2.‎ 答案　C ‎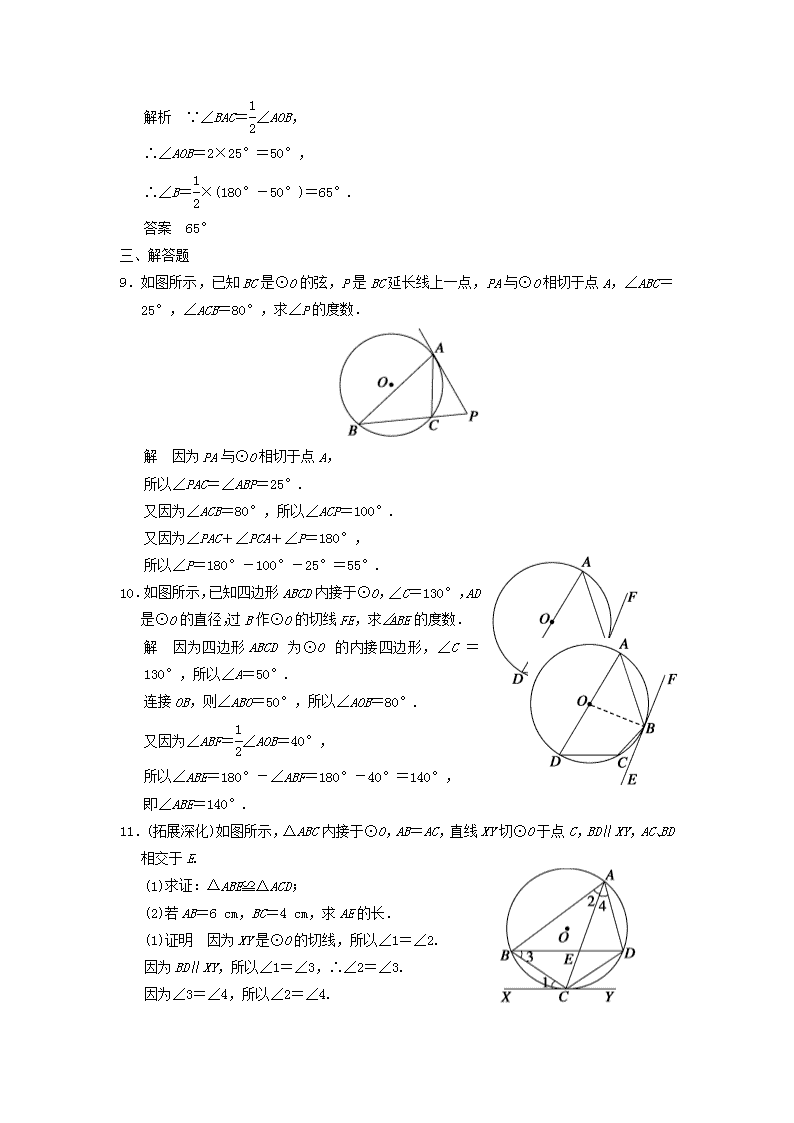3．如图所示，经过⊙O上的点A的切线和弦BC的延长线相交于点P，若∠CAP＝40°，∠ACP＝100°，则∠BAC所对的弧的度数为 ‎(　　)．‎ A．40°　　B．100°　　C．120°　　D．30°‎ 解析　∵AP是⊙O 的切线，∴∠ABC＝∠CAP＝40°，‎ 又∠ACP＝100°，∴∠BAC＝∠ACP－∠ABC＝60°，‎ 即∠BAC所对的弧的度数为120°.‎ 答案　C ‎4．如图所示，AB是⊙O直径，直线EF切⊙O于B，C、D为⊙O上的点，∠CBE＝40°，＝，则∠BCD的度数是 ‎(　　)．‎ A．110° B．115° C．120° D．135°‎ 解析　由AB⊥EF得∠ABC＝90°－∠CBE＝50°，‎ ‎∴2∠ABC＝100°，又＝，∴50°，‎ ‎∴∠BCD＝(180°＋50°)＝115°.‎ 答案　B 二、填空题 ‎5．如图所示，AD切⊙O于点F，FB，FC为⊙O的两弦，请列出图中所有的弦切角________________________．‎ 解析　弦切角的三要素：(1)顶点在圆上，(2)一边与圆相交，(3)一边与圆相切．三要素缺一不可．‎ 答案　∠AFB、∠AFC、∠DFC、∠DFB ‎6．如图所示，已知AB与⊙O相切于点M，且＝，且、的长为圆周长的四分之一，则∠AMC＝________，∠BMC＝________，∠MDC＝________，∠MOC＝______.‎ 解析　弦切角等于所夹弧所对的圆周角，等于所夹弦所对圆心角度数的一半．‎ 答案　45°　135°　45°　90°‎ ‎7．如图所示，AB、AC是⊙O的两条切线，切点分别为B、C，D是优弧上的点，若∠BAC＝80°，那么∠BDC＝________.‎ 解析　连接OB、OC，‎ 则OB⊥AB，OC⊥AC，‎ ‎∴∠BOC＝180°－∠BAC＝100°，‎ ‎∴∠BDC＝∠BOC＝50°.‎ 答案　50°‎ ‎8．如图所示，AC切⊙O于点A，∠BAC＝25°，则∠B的度数为________．‎ 解析　∵∠BAC＝∠AOB，‎ ‎∴∠AOB＝2×25°＝50°，‎ ‎∴∠B＝×(180°－50°)＝65°.‎ 答案　65°‎ 三、解答题 ‎9．如图所示，已知BC是⊙O的弦，P是BC延长线上一点，PA与⊙O相切于点A，∠ABC＝25°，∠ACB＝80°，求∠P的度数．‎ 解　因为PA与⊙O相切于点A，‎ 所以∠PAC＝∠ABP＝25°.‎ 又因为∠ACB＝80°，所以∠ACP＝100°.‎ 又因为∠PAC＋∠PCA＋∠P＝180°，‎ 所以∠P＝180°－100°－25°＝55°.‎ ‎10．如图所示，已知四边形ABCD内接于⊙O，∠C＝130°，AD是⊙O的直径，过B作⊙O的切线FE，求∠ABE的度数．‎ 解　因为四边形ABCD为⊙O的内接四边形，∠C＝130°，所以∠A＝50°.‎ 连接OB，则∠ABO＝50°，所以∠AOB＝80°.‎ 又因为∠ABF＝∠AOB＝40°，‎ 所以∠ABE＝180°－∠ABF＝180°－40°＝140°，‎ 即∠ABE＝140°.‎ ‎11．(拓展深化)如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.‎ ‎(1)求证：△ABE≌△ACD；‎ ‎(2)若AB＝‎6 cm，BC＝‎4 cm，求AE的长．‎ ‎(1)证明　因为XY是⊙O的切线，所以∠1＝∠2.‎ 因为BD∥XY，所以∠1＝∠3，∴∠2＝∠3.‎ 因为∠3＝∠4，所以∠2＝∠4.‎ 因为∠ABD＝∠ACD，又因为AB＝AC，‎ 所以△ABE≌△ACD.‎ ‎(2)解　因为∠3＝∠2，∠ABC＝∠ACB，‎ 所以△BCE∽△ACB，＝，AC·CE＝BC2.‎ 因为AB＝AC＝‎6 cm，BC＝‎4 cm，‎ 所以6·(6－AE)＝16.所以AE＝ cm.‎