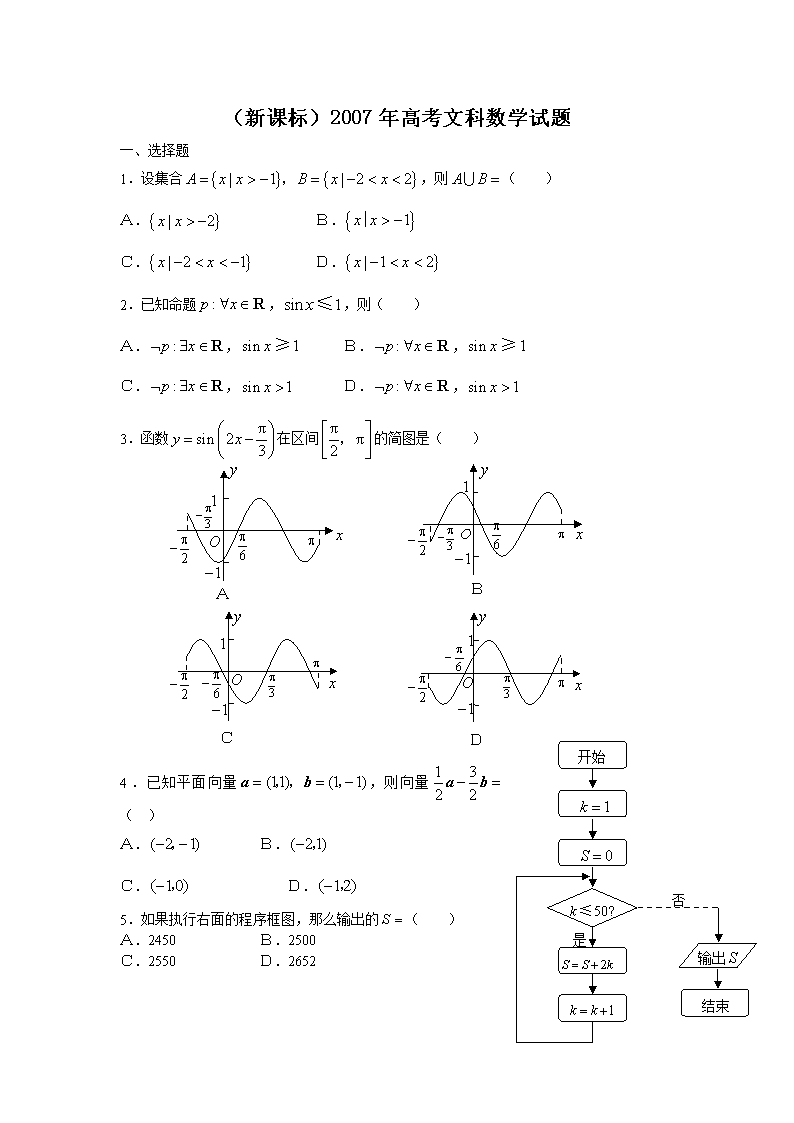历年高考文科数学试题 64页

目 录 （新课标）2007年高考文科数学试题 2‎ （新课标）2008年高考文科数学试题 8‎ （新课标）2009年高考文科数学试题 14‎ （新课标）2010年高考文科数学试题 21‎ （新课标）2011年高考文科数学试题 27‎ （新课标）2012年高考文科数学试题 33‎ （大纲卷）2007年高考文科数学试题 38‎ （大纲卷）2008年高考文科数学试题 42‎ （大纲卷）2009年高考文科数学试题 46‎ （大纲卷）2010年高考文科数学试题 50‎ （大纲卷）2011年高考文科数学试题 55‎ （大纲卷）2012年高考文科数学试题 59‎ ‎（新课标）2007年高考文科数学试题 一、选择题 ‎1．设集合，则（　　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ ‎2．已知命题，，则（　　） ‎ Ａ．， Ｂ．，‎ Ｃ．， Ｄ．，‎ Ａ．‎ Ｂ．‎ Ｃ．‎ Ｄ．‎ ‎3．函数在区间的简图是（　　）‎ 开始 是 否 输出 结束 ‎4．已知平面向量，则向量（　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ ‎5．如果执行右面的程序框图，那么输出的（　　）‎ Ａ．2450 Ｂ．2500 ‎ Ｃ．2550 Ｄ．2652‎ ‎ ‎ ‎6．已知成等比数列，且曲线的顶点是，则等于（　　）‎ Ａ．3 Ｂ．2 Ｃ．1 Ｄ．‎ ‎7．已知抛物线的焦点为，点，‎ 在抛物线上，且，则有（　　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ ‎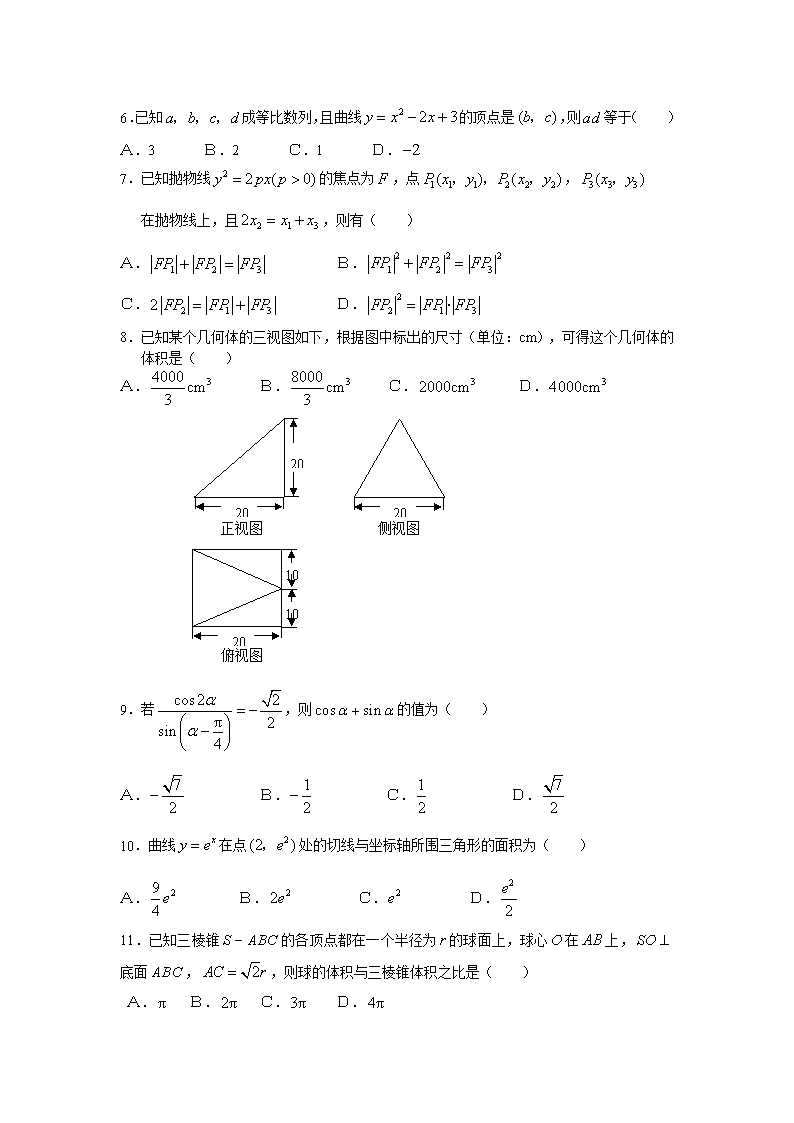8．已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎20 ‎ ‎20 ‎ 正视图 ‎20 ‎ 侧视图 ‎10‎ ‎10‎ ‎20 ‎ 俯视图 ‎9．若，则的值为（　　） ‎ Ａ． Ｂ． 　Ｃ． Ｄ．‎ ‎10．曲线在点处的切线与坐标轴所围三角形的面积为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎11．已知三棱锥的各顶点都在一个半径为的球面上，球心在上，底面，，则球的体积与三棱锥体积之比是（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎12．甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表 甲的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎5‎ ‎5‎ ‎5‎ ‎5‎ 乙的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎6‎ ‎4‎ ‎4‎ ‎6‎ 丙的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎4‎ ‎6‎ ‎6‎ ‎4‎ ‎ 分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则有（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 二、填空题：‎ ‎13．已知双曲线的顶点到渐近线的距离为2，焦点到渐近线的距离为6，‎ 则该双曲线的离心率为　　　　　．‎ ‎14．设函数为偶函数，则　　　　．‎ ‎ ‎ ‎15．是虚数单位，　　　　　．（用的形式表示，）‎ ‎16．已知是等差数列，，其前5项和，则其公差　　　　．‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17．如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个测点与．现测得，并在点测得塔顶的仰角为，求塔高．‎ ‎ ‎ ‎ ‎ ‎18．如图，为空间四点．在中，．等边三角形以为轴运动．‎ ‎（Ⅰ）当平面平面时，求；‎ ‎（Ⅱ）当转动时，是否总有？证明你的结论．‎ ‎19．设函数，‎ ‎（Ⅰ）讨论的单调性； （Ⅱ）求在区间的最大值和最小值．‎ ‎20．设有关于的一元二次方程．‎ ‎（Ⅰ）若是从四个数中任取的一个数，是从三个数中任取的一个数，求上述方程有实根的概率．‎ ‎（Ⅱ）若是从区间任取的一个数，是从区间任取的一个数，求上述方程有实根的概率．‎ ‎ ‎ ‎21．在平面直角坐标系中，已知圆的圆心为，过点 且斜率为的直线与圆相交于不同的两点．‎ ‎（Ⅰ）求的取值范围；‎ ‎（Ⅱ）是否存在常数，使得向量与共线？如果存在，求值；‎ 如果不存在，请说明理由．‎ ‎22．Ａ 选修4－1：几何证明选讲，如图，已知是的切线，为切点，是的割线，与交于两点，圆心在的内部，点是的中点．‎ ‎（Ⅰ）证明四点共圆； （Ⅱ）求的大小．‎ ‎ ‎ ‎22．Ｂ 选修4－4：坐标系与参数方程和的极坐标方程分别为：‎ ‎．‎ ‎（Ⅰ）把和的极坐标方程化为直角坐标方程；‎ ‎（Ⅱ）求经过，交点的直线的直角坐标方程．‎ 22、 C 选修4-5 不等式选讲，设函数．‎ ‎（I）解不等式；（II）求函数的最小值．‎ ‎（新课标）2008年高考文科数学试题 一、选择题：‎ ‎1、已知集合M ={ x|(x + 2)(x－1) < 0 }，N ={ x| x + 1 < 0 }，则M∩N =（ ）‎ A. (－1，1) B. (－2，1) ‎ C. (－2，－1) D. (1，2)‎ 是 否 开始 输入a,b,c x=a b>x 输出x 结束 x=b x=c 否 是 ‎2、双曲线的焦距为（ ）‎ A. 3 B. 4 C. 3 D. 4‎ ‎3、已知复数，则（ ）‎ A. 2 B. －2 C. 2i D. －2i ‎4、设，若，则（ ）‎ A. B. C. D. ‎ ‎5、已知平面向量=（1，－3），=（4，－2），与垂直，‎ 则是（ ）‎ A. －1 B. 1 C. －2 D. 2‎ ‎6、右面的程序框图，如果输入三个实数a、b、c，要求输出这三 个数中最大的数，那么在空白的判断框中，应该填入下面四个 选项中的（ ）‎ A. c > x B. x > c C. c > b D. b > c ‎ ‎ ‎7、已知，则使得都成立的取值范围是（ ）‎ A.（0，） B. （0，） C. （0，） D. （0，）‎ ‎8、设等比数列的公比，前n项和为，则（ ）‎ A. 2 B. 4 C. D. ‎ ‎9、平面向量，共线的充要条件是（ ）‎ A. ，方向相同 B. ，两向量中至少有一个为零向量 ‎ C. ， D. 存在不全为零的实数，，‎ ‎10、点P（x，y）在直线4x + 3y = 0上，且满足－14≤x－y≤7，则点P到坐标原点距离的取值范围是（ ）‎ A. [0，5] B. [0，10] C. [5，10] D. [5，15]‎ ‎11、函数的最小值和最大值分别为（ ）‎ A. －3，1 B. －2，2 C. －3， D. －2，‎ ‎12、已知平面α⊥平面β，α∩β= l，点A∈α，Al，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（ ）‎ A. AB∥m B. AC⊥m C. AB∥β D. AC⊥β 二、填空题 ‎13、已知{an}为等差数列，a3 + a8 = 22，a6 = 7，则a5 = ____________‎ ‎14、一个六棱柱的底面是正六边形，其侧棱垂直底面。已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为，底面周长为3，那么这个球的体积为 _________‎ ‎15、过椭圆的右焦点作一条斜率为2的直线与椭圆交于A、B两点，O为坐标原点，则△OAB的面积为______________‎ ‎16、从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度（单位：mm），结果如下：‎ 甲品种：271　273　280　285　287　292　294　295　301　303　303　307‎ ‎ 308　310　314　319　323　325　328　331　334　337　352‎ 乙品种：284　292　295　304　306　307　312　313　315　315　316　318　318‎ ‎ 320　322　322　324　327　329　331　333　336　337　343　356‎ 由以上数据设计了如下茎叶图 根据以上茎叶图，对甲、乙两品种棉花的纤维长度作比较，写出两个统计结论：‎ ‎①　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　；‎ ‎②　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　.‎ 三、解答题：解答须写出文字说明，证明过程和演算步骤。‎ ‎17、如图，△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB=90，BD交AC于E，AB=2。‎ ‎（1）求cos∠CBE的值； （2）求AE。‎ ‎18、如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出（单位：cm）。‎ ‎（1）在正视图下面，按照画三视图的要求画出该多面体的俯视图；‎ ‎（2）按照给出的尺寸，求该多面体的体积；‎ ‎（3）在所给直观图中连结，证明：∥面EFG。‎ ‎19、为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查，6人得分情况如下：5，6，7，8，9，10。把这6名学生的得分看成一个总体。‎ ‎（1）求该总体的平均数；‎ ‎（2）用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本。求该样本平均数与总体平均数之差的绝对值不超过0.5的概率。‎ ‎20、已知m∈R，直线l：和圆C：。‎ ‎（1）求直线l斜率的取值范围；‎ ‎（2）直线l能否将圆C分割成弧长的比值为的两段圆弧？为什么？‎ ‎21、设函数，曲线在点处的切线方程为。‎ ‎（1）求的解析式；‎ ‎（2）证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为定值，并求此定值。‎ ‎22、A 选修4－1：几何证明选讲，‎ 如图，过圆O外一点M作它的一条切线，切点为A，过A作直线AP垂直直线OM，垂足为P。‎ ‎（1）证明：OM·OP = OA2；‎ ‎（2）N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点。过B点的切线交直线ON于K。证明：∠OKM = 90°。‎ ‎22、B 选修4－4：坐标系与参数方程：‎ 已知曲线C1：，曲线C2：。‎ ‎（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；‎ ‎（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线，。写出， 的参数方程。与公共点的个数和C1与C2公共点的个数是否相同？说明你的理由。‎ ‎22、C 选修4-5 ：不等式选讲，已知函数．‎ ‎（Ⅰ）作出函数的图像； （Ⅱ）解不等式．‎ ‎1‎ ‎1‎ O x y ‎（新课标）2009年高考文科数学试题 一、选择题：‎ ‎1、已知集合,则（ ）‎ ‎ (A) (B) (C) (D) ‎ ‎2、 复数（ ）‎ ‎（A） （B） （C） (D)‎ ‎3、对变量 有观测数据（，）（），得散点图1；对变量有观测数据（，）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断（ ）‎ ‎（A）变量x 与y 正相关，u 与v 正相关 （B）变量x 与y 正相关，u 与v 负相关 ‎（C）变量x 与y 负相关，u 与v 正相关 （D）变量x 与y 负相关，u 与v 负相关 ‎4、有四个关于三角函数的命题：w.w.w.k.s.5.u.c.o.m ‎ ‎：xR, += : , ‎ ‎: x, : ‎ 其中假命题的是（ ）‎ ‎（A）， （B）， （3）， （4），‎ ‎5、已知圆：+=1，圆与圆关于直线对称，则圆的方程为（ ）‎ ‎（A）+=1 （B）+=1‎ ‎（C）+=1 （D）+=1‎ ‎6、设满足则（ ）‎ ‎（A）有最小值2，最大值3 （B）有最小值2，无最大值 ‎（C）有最大值3，无最小值 （D）既无最小值，也无最大值 ‎7、已知，向量与垂直，则实数的值为 ‎（A） （B） （C） （D）‎ ‎8、等差数列的前n项和为，已知，,则 ‎（A）38 （B）20 （C）10 （D）9‎ ‎9、如图，正方体的棱线长为1，线段上有两个动点E，F，且 则下列结论中错误的是 ‎ ‎（A） ‎ ‎（B）‎ ‎（C）三棱锥的体积为定值 ‎（D）‎ ‎10、如果执行右边的程序框图，输入，那么输出的各个数的和等于（）w.w.w.k.s.5.u.c.o.m （A）3 （B） 3.5 （C） 4 （D）4.5‎ ‎11、一个棱锥的三视图如图，则该棱锥的全面积（单位：）为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎12、用min{a,b,c}表示a,b,c三个数中的最小值，设 (x0),则的最大值为（ ）‎ ‎（A） 4 （B） 5 （C） 6 （D） 7‎ 二 填空题w.w.w.k.s.5.u.c.o.m ‎ ‎13、曲线在点（0,1）处的切线方程为 。‎ ‎14、已知抛物线C的顶点坐标为原点，焦点在x轴上，直线y=x与抛物线C交于A，B两点，若为的中点，则抛物线C的方程为 。‎ ‎15、等比数列{}的公比, 已知=1，，则{}的前4项和 ‎= ‎ ‎16、已知函数的图像如图所示，则 。‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤。‎ ‎17、 如图，为了解某海域海底构造，在海平面内一条直线上的A，B，C三点进行测量，已知，，于A处测得水深，于B处测得水深 ‎，于C处测得水深，求∠DEF的余弦值。 w.w.w.k.s.5.u.c.o.m ‎ ‎18、如图，在三棱锥中，⊿是等边三角形，∠PAC=∠PBC=90 º ‎（Ⅰ）证明：AB⊥PC ‎（Ⅱ）若，且平面⊥平面，求三棱锥体积。：‎ ‎19、某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）.现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）.‎ ‎（Ⅰ）A类工人中和B类工人各抽查多少工人？‎ ‎（Ⅱ）从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2‎ 表1：‎ 生产能力分组 人数 ‎4‎ ‎8‎ ‎5‎ ‎3‎ 表2：‎ 生产能力分组 人数 ‎ 6‎ ‎ y ‎ 36‎ ‎ 18‎ ‎（i）先确定x，y，再在答题纸上完成下列频率分布直方图。就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论） ‎ ‎ ‎ ‎ 图1 A类工人生产能力的频率分布直方图 图2 B类工人生产能力的频率分布直方图 ‎ (ii) 分别估计类工人和类工人生产能力的平均数，并估计该工厂工人和生产能力的平均数（同一组中的数据用该区间的中点值作代表）。‎ ‎20、已知椭圆的中心为直角坐标系的原点，焦点在轴上，它的一个项点到两个 焦点的距离分别是7和1‎ ‎（1）求椭圆的方程，‎ ‎（2）若为椭圆的动点，为过且垂直于轴的直线上的点，（e为椭圆C的离心率），求点的轨迹方程，并说明轨迹是什么曲线。‎ ‎21、已知函数.‎ (1) 设，求函数的极值；‎ (2) 若，且当时，12a恒成立，试确定的取值范围.‎ ‎ ‎ ‎22 A 选修4—1；几何证明选讲,如图，已知ABC中的两条角平分线和相交于，B=60，在上，且。w.w.w.k.s.5.u.c.o.m ‎ ‎（1）证明：四点共圆； （2）证明：CE平分DEF。‎ ‎ ‎ ‎22 B 已知曲线C： （t为参数）， C：（为参数）。‎ ‎（1）化C，C的方程为普通方程，并说明它们分别表示什么曲线；‎ ‎（2）若C上的点P对应的参数为，Q为C上的动点，求中点到直线 ‎ （t为参数）距离的最小值。w.w.w.k.s.5.u.c.o.m ‎ ‎22 C 不等式选讲，如图，为数轴的原点，为数轴上三点，为线段上的动点，设表示与原点的距离， 表示到距离4倍与到距离的6倍的和.‎ ‎（1）将表示为的函数；‎ ‎（2）要使的值不超过70， 应该在什么范围内取值？‎ ‎ w.w.w.k.s.5.u.c.o.m ‎ ‎ w.w.w.k.s.5.u.c.o.m ‎ ‎（新课标）2010年高考文科数学试题 一、选择题：‎ ‎1、已知集合，则（ ）‎ ‎(A)(0,2) (B)[0,2] (C){0,2] (D){0,1,2}‎ ‎2、a，b为平面向量，已知a=（4，3），2a+b=（3，18），则a，b夹角的余弦值等于（ ）‎ ‎（A） （B） （C） （D）‎ ‎3、已知复数，则=（ ）‎ ‎(A) （B） （C）1 （D）2‎ ‎4、曲线在点（1,0）处的切线方程为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎5、中心在远点，焦点在轴上的双曲线的一条渐近线经过点（4,2），则它的离心率为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎6、如图，质点在半径为2的圆周上逆时针运动，其初始位置为（，），角速度为1，那么点到轴距离关于时间的函数图像大致为（ ）‎ ‎7、设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上，则该球的表面积为（ ）‎ ‎ （A）3a2 （B）6a2 （C）12a2 （D） 24a2‎ ‎8、如果执行右面的框图，输入N=5，则输出的数等于（ ）‎ ‎（A）‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎ 9、设偶函数f(x)满足f(x)=2x-4 (x0），则=（ ）‎ ‎ （A） （B）‎ ‎（C） （D）‎ ‎10、若= -，a是第一象限的角，则=( )‎ ‎（A）- （B） （C） （D）‎ ‎11、已知ABCD的三个顶点为A（-1，2），B（3，4），C（4，-2），点（x，y）在ABCD的内部，则z=2x-5y的取值范围是( )‎ ‎（A）（-14，16） （B）（-14，20） （C）（-12，18） （D）（-12，20）‎ ‎12、已知函数f(x)=， 若a，b，c均不相等，且f(a)= f(b)= f(c)，则abc的取值范围是（ ）‎ ‎（A）（1，10） （B）(5，6) （C）(10，12) （D）(20，24)‎ 二、填空题：‎ ‎13、圆心在原点上与直线相切的圆的方程为 。‎ ‎14、设函数为区间上的图像是连续不断的一条曲线，且恒有，可以用随机模拟方法计算由曲线及直线，，所围成部分的面积，先产生两组每组个，区间上的均匀随机数和，由此得到V个点。再数出其中满足的点数，那么由随机模拟方法可得S的近似值为___________‎ ‎15、一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)‎ ‎①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱 ‎16、在中，D为BC边上一点，,,.若,则BD=_____‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤。‎ ‎17、设等差数列满足，。‎ ‎（Ⅰ）求的通项公式； （Ⅱ）求的前项和及使得最大的序号的值。‎ ‎18、如图，已知四棱锥的底面为等腰梯形，∥,,垂足为，是四棱锥的高。‎ ‎（Ⅰ）证明：平面 平面;‎ ‎（Ⅱ）若,60°,求四棱锥的体积。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎19、为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如下：‎ ‎ ‎ 性别 是否需要 男 女 需要 ‎40‎ ‎30‎ 不需要 ‎160‎ ‎270‎ ‎（Ⅰ）估计该地区老年人中，需要志愿提供帮助的老年人的比例；‎ ‎（Ⅱ）能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？‎ P(K2≥k)‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎（Ⅲ）根据（Ⅱ）的结论，能否提出更好的调查办法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由。 附：‎ ‎ ‎ ‎ K2＝ ‎20、设,分别是椭圆E：+=1（0﹤b﹤1）的左、右焦点，过的直线与E相交于A、B两点，且，，成等差数列。‎ ‎（Ⅰ）求 （Ⅱ）若直线的斜率为1，求b的值。‎ ‎ ‎ ‎21、设函数 ‎（Ⅰ）若a=，求的单调区间； （Ⅱ）若当≥0时≥0，求a的取值范围 ‎22、A 选修4—1：几何证明选讲，如图：已知圆上的弧，过C点的圆的切线与BA的延长线交于 E点，‎ 证明：（Ⅰ）=。 （Ⅱ）=BE x CD。‎ ‎22、B 选修4－4：坐标系与参数方程：‎ 已知直线C1：(t为参数)，圆C2：(θ为参数)．‎ ‎(1)当α＝时，求C1与C2的交点坐标；‎ ‎(2)过坐标原点O作C1的垂线，垂足为A，P为OA的中点．当α变化时，求P点轨迹的参数方程，并指出它是什么曲线．‎ ‎22、C 选修4—5：不等式选讲，设函数= + 1。‎ ‎ （Ⅰ）画出函数y=的图像：‎ ‎ （Ⅱ）若不等式≤ax的解集非空，求n的取值范围 ‎ （新课标）2011年高考文科数学试题 一、选择题：‎ ‎1．已知集合M={0，1，2，3，4}，N={1，3，5}，P=M，则P的子集共有（ ）‎ ‎ A．2个 B．4个 C．6个 D．8个 ‎2．复数（ ）‎ ‎ A． B． C． D．‎ ‎3．下列函数中，既是偶函数又在单调递增的函数是（ ）‎ ‎ A． B． C． D．‎ ‎4．椭圆的离心率为（ ）‎ ‎ A． B． C． D．‎ ‎5．执行右面的程序框图，如果输入的N是6，那么输出的p是（ ）‎ A．120 ‎ B． 720 ‎ C． 1440 ‎ D． 5040‎ ‎6．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（ ）‎ ‎ A． B． C． D．‎ ‎7．已知角的顶点与原点重合，始边与x轴的正半轴重合，终边在直线上，则=‎ ‎ A． B． C． D．‎ ‎8．在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为（ ）‎ ‎9．已知直线l过抛物线C的焦点，且与C的对称轴垂直，l与C交于A，B两点，，P为C的准线上一点，则的面积为（ ）‎ ‎ A．18 B．24 C． 36 D． 48‎ ‎10．在下列区间中，函数的零点所在的区间为（ ）‎ ‎ A． B． C． D．‎ ‎11．设函数，则（ ）‎ ‎ A．在单调递增，其图象关于直线对称 ‎ B．在单调递增，其图象关于直线对称 ‎ C．在单调递减，其图象关于直线对称 ‎ D．在单调递减，其图象关于直线对称 ‎12．已知函数的周期为2，当时，那么函数的图象与函数的图象的交点共有（ ）‎ ‎ A．10个 B．9个 C．8个 D．1个 二、填空题 ‎13．已知a与b为两个不共线的单位向量，k为实数，若向量a+b与向量ka-b垂直，则k=_____________．‎ ‎14．若变量x，y满足约束条件，则的最小值是_________．‎ ‎15．中，，则的面积为_________．‎ ‎16．已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为________．‎ 三、解答题：解答应写文字说明，证明过程或演算步骤．‎ ‎17．已知等比数列中，，公比．‎ ‎（I）为的前n项和，证明：‎ ‎（II）设，求数列的通项公式．‎ ‎18．如图，四棱锥中，底面ABCD为平行四边形，，，底面ABCD．‎ ‎ （I）证明：； （II）设PD=AD=1，求棱锥D-PBC的高．‎ ‎19．某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每产品的质量指标值，得到时下面试验结果：‎ A配方的频数分布表：‎ 指标值分组 ‎[90，94）‎ ‎[94，98）‎ ‎[98，102）‎ ‎[102，106）‎ ‎[106，110]‎ 频数 ‎8‎ ‎20‎ ‎42‎ ‎22‎ ‎8‎ B配方的频数分布表：‎ 指标值分组 ‎[90，94）‎ ‎[94，98）‎ ‎[98，102）‎ ‎[102，106）‎ ‎[106，110]‎ 频数 ‎4‎ ‎12‎ ‎42‎ ‎32‎ ‎10‎ ‎（I）分别估计用A配方，B配方生产的产品的优质品率；‎ ‎（II）已知用B配方生产的一种产品利润y（单位：元）与其质量指标值t的关系式为 估计用B配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述100件产品平均一件的利润．‎ ‎20．在平面直角坐标系xOy中，曲线与坐标轴的交点都在圆C上．‎ ‎ （I）求圆C的方程；‎ ‎ （II）若圆C与直线交于A，B两点，且求a的值．‎ ‎21、已知函数，曲线在点处的切线方程为．‎ ‎ （I）求a，b的值； （II）证明：当x>0，且时，．‎ ‎22．A 选修4-1：几何证明选讲，如图，D，E分别为的边AB，AC上的点，且不与的顶点重合．已知AE的长为m，AC的长为n，AD，AB的长是关于x的方程的两个根．‎ ‎（I）证明：C，B，D，E四点共圆；‎ ‎（II）若，且求C，B，D，E所在圆的半径．‎ ‎22、B 坐标系与参数方程，在直角坐标系xOy中，曲线的参数方程为为参数），M为上的动点，P点满足，点P的轨迹为曲线．‎ ‎ （I）求的方程；‎ ‎ （II）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线与的异于极点的交点为A，与的异于极点的交点为B，求|AB|．‎ ‎22、C 选修4-5：不等式选讲，设函数，其中．‎ ‎（I）当a=1时，求不等式的解集．‎ ‎（II）若不等式的解集为｛x|，求a的值．‎ ‎（新课标）2012年高考文科数学试题 一、选择题：‎ ‎1、已知集合A={x|x2－x－2<0}，B={x|－1b>0)的左、右焦点，P为直线x=上一点，△F1PF2是底角为30°的等腰三角形，则E的离心率为（ ）‎ ‎（A） （B） （C） （D） ‎5、已知正三角形ABC的顶点A(1,1)，B(1,3)，顶点C在第一象限，若点（x，y）在△ABC内部，则z=－x+y的取值范围是（ ）‎ ‎（A）(1－，2) （B）(0，2) （C）(－1，2) （D）(0，1+)‎ ‎6、如果执行右边的程序框图，输入正整数N(N≥2)和实数a1,a2,…,aN，输出A,B，则（ ）‎ ‎（A）A+B为a1,a2,…,aN的和 ‎（B）为a1,a2,…,aN的算术平均数 ‎（C）A和B分别是a1,a2,…,aN中最大的数和最小的数 ‎（D）A和B分别是a1,a2,…,aN中最小的数和最大的数 ‎7、如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为 ‎（A）6 （B）9 （C）12 （D）18‎ ‎ ‎ ‎ ‎ ‎8、平面截球O的球面所得圆的半径为1，球心O到平面的距离为，此球的体积为（ ） ‎ ‎（A）π （B）4π （C）4π （D）6π ‎9、已知ω>0，0<φ<π，直线x=和x=是f(x)=sin(ωx+φ)图像的两条相邻的对称轴，φ=（ ）‎ ‎（A） （B） （C） （D）‎ ‎10、等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，|AB|=4，则C的实轴长为（ ）‎ ‎（A） （B）2 （C）4 （D）8‎ ‎11、当00)的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F交l于B，D两点。‎ ‎（I）若∠BFD=90°,△ABD的面积为4，求p的值及圆F的方程；‎ ‎（II）若A，B，F三点在同一直线m上，直线n与m平行，且n与C 只有一个公共点，求坐标原点到m，n距离的比值。‎ ‎ ‎ ‎ ‎ ‎21、设函数f(x)= ex－ax－2，‎ ‎(Ⅰ)求f(x)的单调区间 ‎(Ⅱ)若a=1，k为整数，且当x>0时，(x－k) f´(x)+x+1>0，求k的最大值 ‎22、A 选修4-1：几何证明选讲如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF//AB，‎ 证明：(Ⅰ)CD=BC； (Ⅱ)△BCD∽△GBD ‎22、B 已知曲线C1的参数方程是(φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上，且A、B、C、D以逆时针次序排列，点A的极坐标为(2，)‎ ‎(Ⅰ)求点A、B、C、D 的直角坐标；‎ ‎(Ⅱ)设P为C1上任意一点，求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围。‎ ‎22、C 选修4—5：不等式选讲，已知函数f(x) = |x + a| + |x－2|.‎ ‎(Ⅰ)当a =－3时，求不等式f(x)≥3的解集；‎ ‎(Ⅱ)若f(x)≤|x－4|的解集包含[1,2]，求a的取值范围。‎ ‎（大纲卷）2007年高考文科数学试题 一、选择题 ‎1、( )‎ ‎ （A） （B） （C） （D）‎ ‎2、设集合CU=（A）=( )‎ ‎ （A）{2} （B）{3} （C）{1,2,4} （D）{1,4}‎ ‎3、函数的一个单调增区间是( )‎ ‎ （A） （B） （C） （D）‎ ‎4、下列四个数中最大的是( )‎ ‎ （A） （B） （C） （D）‎ ‎5、不等式的解集是( )‎ ‎ （A）（－3，2） （B）（2，+∞）‎ ‎（C） （D）‎ ‎6、在△ABC中，已知D是AB边上一点，若( )‎ ‎ （A） （B） （C） （D）‎ ‎7、已知正三棱锥的侧棱长是底面边长的2倍，则侧棱与底面所成角的余弦值等于( )‎ ‎（A） （B） （C） （D）‎ ‎8、已知双曲线的一条切线的斜率为，则切点的横坐标为( )‎ ‎ （A）1 （B）2 （C）3 （D）4‎ ‎9、把函数的图像按向量a =（2,3）平移,得到的图像,则( )‎ ‎ （A） （B） （C） （D）‎ ‎10、5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同的 报名方法共有( )‎ ‎（A）10种 （B）20种 （C）25种 （D）32种 ‎11、已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于( )‎ ‎（A） （B） （C） （D）‎ ‎12、设F1、F2分别为双曲线的左、右焦点,若点P在双曲线上,且 ‎( )‎ ‎（A） （B）2 （C） （D）2‎ 二、填空题 ‎13、一个总体含有100个个体，以简单随机抽样方式从该总体中抽取一个容量为5的样本，则指定的某个个体被抽到的概率为 .‎ ‎14、已知数列的通项，其前n项和为Sn= .‎ ‎15、一个正四棱柱的各个顶点在一个直径为2cm的球面上，如果正四棱柱的底面边长为1cm，那么该棱柱的表面积为 cm2.‎ ‎16、的展开式中常数项为 .（用数字作答）‎ 三、解答题：‎ ‎17、设等比数列的公比,前n项和为Sn.已知求的通项公式。‎ ‎18、在△ABC中，已知内角设内角B=x，周长为y.‎ ‎（Ⅰ）求函数y=f(x)的解析式和定义域； （Ⅱ）求y的最大值.‎ ‎19、从某批产品中，有放回地抽取产品二次，每次随机抽取1件.假设事件A：“取出的2件产品中至多有1件是二等品”的概率P（A）=0.96.‎ ‎（Ⅰ）求从该批产品中任取1件是二等品的概率p;‎ ‎（Ⅱ）若该批产品共100件，从中任意抽取2件, 求事件B：“取出的2‎ 件产品中至少有一件二等品”的概率P(B).‎ ‎ ‎ ‎20、如图，在四棱锥S—ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD, E、F分别为AB、SC的中点.‎ ‎（Ⅰ）证明EF//平面SAD. （Ⅱ）设SD=2DC. 求二面角A—EF—D的大小.‎ ‎21、在直角坐标系xOy中，以O为圆心的圆与直线相切.‎ ‎（Ⅰ）求圆O的方程；‎ ‎（Ⅱ）圆O与x轴相交于A、B两点，圆内的动点P使|PA|、|PO|、|PB| 成等比数列，求 ‎·的取值范围.‎ ‎22、已知函数，在处取得极大值，在处取得极小值，且 ‎ （Ⅰ）证明a>0； （Ⅱ）求z=a+3b的取值范围.‎ ‎（大纲卷）2008年高考文科数学试题 一、选择题 1．若且是，则是（ ）‎ A．第一象限角 B． 第二象限角 C． 第三象限角 D． 第四象限角 ‎2．设集合，（ ）‎ A． B． C． D．‎ 3．原点到直线的距离为（ ）‎ A．1 B． C．2 D．‎ ‎4．函数的图像关于（ ）‎ A．轴对称 B． 直线对称 C． 坐标原点对称 D． 直线对称 5．若，则（ ）‎ A．<< B． << C． << D． <<‎ ‎6．设变量满足约束条件：，则的最小值为（ ）‎ A． B． C． D．‎ 7．设曲线在点（1，）处的切线与直线平行，则（ ）‎ A．1 B． C． D．‎ ‎8．正四棱锥的侧棱长为，侧棱与底面所成的角为，则该棱锥的体积为（ ）‎ A．3 B．‎6 ‎ C．9 D．18 ‎ 9．的展开式中的系数是（ ）‎ A． B． C．3 D．4 ‎ ‎10．函数的最大值为（ ）‎ A．1 B． C． D．2‎ 11．设是等腰三角形，，则以为焦点且过点的双曲线的离心率为（ ）‎ A． B． C． D．‎ ‎12．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ）‎ A．1 B． C． D．2‎ 二、填空题 13．设向量，若向量与向量共线，则 ．‎ ‎14．从10名男同学，6名女同学中选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的不同选法共有 种（用数字作答）‎ 15．已知是抛物线的焦点，是上的两个点，线段AB的中点为，则的面积等于 ．‎ ‎16．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：‎ 充要条件① ；‎ 充要条件② ．‎ ‎（写出你认为正确的两个充要条件）‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ 17．在中，，． ‎ ‎（Ⅰ）求的值； （Ⅱ）设，求的面积．‎ ‎18．等差数列中，且成等比数列，求数列前20项的和．‎ 19‎ ‎．甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹．根据以往资料知，甲击中8环，9环，10环的概率分别为0.6，0.3，0.1，乙击中8环，9环，10环的概率分别为0.4，0.4，0.2．‎ 设甲、乙的射击相互独立．‎ ‎（Ⅰ）求在一轮比赛中甲击中的环数多于乙击中环数的概率；‎ ‎（Ⅱ）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率．‎ ‎20．如图，正四棱柱中，，点在上且．‎ ‎（Ⅰ）证明：平面； （Ⅱ）求二面角的大小．‎ A B C D E A1‎ B1‎ C1‎ D1‎ ‎ ‎ 21．设，函数．‎ ‎（Ⅰ）若是函数的极值点，求的值；‎ ‎（Ⅱ）若函数，在处取得最大值，求的取值范围．‎ ‎22．设椭圆中心在坐标原点，是它的两个顶点，直线与AB相交于点D，与椭圆相交于E、F两点．‎ ‎（Ⅰ）若，求的值；‎ ‎（Ⅱ）求四边形面积的最大值．‎ ‎（大纲卷）2009年高考文科数学试题 一、选择题 ‎1、已知全集U={1，2，3，4，5，6，7，8}，M ={1，3，5，7}，N ={5，6，7}，则Cu( MN)= ‎ ‎(A) {5，7} （B） {2，4} （C）{‎2.4.8‎} （D）{1，3，5，6，7}‎ ‎2、函数y=(x0)的反函数是( )‎ ‎（A）（x0） （B）（x0） （B）（x0） （D）（x0） 3、 函数y=的图像( )‎ ‎（A） 关于原点对称 （B）关于主线对称 ‎（C） 关于轴对称 （D）关于直线对称 ‎4、已知△ABC中，，则( )‎ ‎(A) (B) (C) (D) ‎ ‎5、 已知正四棱柱中，=，为重点，则异面直线 与所形成角的余弦值为( )‎ ‎（A） (B) (C) (D) w.w.w.k.s.5.u.c.o.m ‎ ‎6、已知向量a = (2,1)， a·b = 10，︱a + b ︱= ，则︱b ︱=( )‎ ‎ （A） （B） （C）5 （D）25‎ ‎7、设则( )‎ ‎（A） （B） （C） （D）‎ ‎8、双曲线的渐近线与圆相切，则r=( )‎ ‎（A） （B）2 （C）3 （D）6‎ ‎9、若将函数的图像向右平移个单位长度后，与函数的图像重合，则的最小值为( )‎ ‎(A) (B) (C) (D) w.w.w.k.s.5.u.c.o.m ‎ ‎10、甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中恰有1门相同的选法有（ ）‎ ‎（A）6种 （B）12种 （C）24种 （D）30种 ‎11、已知直线与抛物线C:相交A、B两点，F为C的焦点。若,则k=( )‎ ‎(A) (B) (C) (D)‎ ‎12、纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现在沿该正方体的一些棱将正方体剪开、外面朝上展平，得到右侧的平面图形，则标“△”的面的方位是 ‎△‎ 上 东 ‎（A）南 （B）北 （C）西 （D）下 ‎ w.w.w.k.s.5.u.c.o.m ‎ ‎ ‎ 二．填空题：‎ ‎13、设等比数列{}的前n项和为。若，则= ‎ ‎14、的展开式中的系数为 w.w.w.k.s.5.u.c.o.m ‎ ‎15、已知圆O：和点A（1，2），则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 ‎ ‎16、设OA是球O的半径，M是OA的中点，过M且与OA成45°角的平面截球O的表面得到圆C。若圆C的面积等于，则球O的表面积等于 ‎ 三、解答题：解答题应写出文字说明，证明过程或演算步骤。‎ ‎17、已知等差数列{}中，求{}前n项和. w.w.w.k.s.5.u.c.o.m ‎ ‎18、设△ABC的内角A、B、C的对边长分别为a、b、c，,，求B.‎ ‎19、 如图，直三棱柱ABC-A1B1C1中，AB⊥AC,D、E分别为AA1、B1C的中点，DE⊥平面BCC1‎ ‎（Ⅰ）证明：AB=AC w.w.w.k.s.5.u.c.o.m ‎ ‎（Ⅱ）设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小 A C B A1‎ B1‎ C1‎ D E ‎20、‎ 某车间甲组有10名工人，其中有4名女工人；乙组有10名工人，其中有6名女工人。现采用分层抽样（层内采用不放回简单随即抽样）从甲、乙两组中共抽取4名工人进行技术考核。‎ ‎（Ⅰ）求从甲、乙两组各抽取的人数；‎ ‎（Ⅱ）求从甲组抽取的工人中恰有1名女工人的概率；‎ ‎（Ⅲ）求抽取的4名工人中恰有2名男工人的概率。w.w.w.k.s.5.u.c.o.m ‎ ‎21、设函数 ，其中常数a>1‎ ‎(Ⅰ)讨论f(x)的单调性; (Ⅱ)若当x≥0时，f(x)>0恒成立，求a的取值范围。‎ w.w.w.k.s.5.u.c.o.m ‎ ‎22、已知椭圆C: 的离心率为，过右焦点F的直线l与C相交于A、B两点，当，当l的斜率为1时，坐标原点O到l的距离为 ‎（Ⅰ）求a,b的值；‎ ‎（Ⅱ）C上是否存在点P，使得当l绕F转到某一位置时，有 成立？若存在，求出所有的P的坐标与l的方程；若不存在，说明理由。‎ ‎（大纲卷）2010年高考文科数学试题 一、 选择题 ‎1、设全集( )‎ ‎（A） （B） （C） （D）‎ ‎2、不等式＜0的解集为( )‎ ‎（A） （B） （C） （D）‎ ‎3、已知，则( )‎ ‎（A）（B）（C）（D）‎ ‎4、函数y=1+ln(x-1)(x>1)的反函数是（ ）‎ ‎（A）y=-1(x>0) (B) y=+1(x>0) (C) y=-1(x R) (D）y=+1 (x R)‎ ‎5、若变量x,y满足约束条件 则z=2x+y的最大值为( )‎ ‎（A）1 (B)2 (C)3 (D)4‎ ‎6、如果等差数列中，++=12，那么++…+=( )‎ ‎（A）14 (B) 21 (C) 28 (D) 35‎ ‎7、若曲线在点处的切线方程是，则( )‎ ‎（A） (B) (C) (D) ‎ ‎8、已知三棱锥中，底面为边长等于2的等边三角形，垂直于底面，=3，那么直线与平面所成角的正弦值为( )‎ ‎（A） (B) (C) (D) ‎ ‎9、将标号为1，2，3，4，5，6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1，2的卡片放入同一信封，则不同的方法共有( )‎ ‎（A） 12种 (B) 18种 (C) 36种 (D) 54种 ‎10、△ABC中，点D在边AB上，CD平分∠ACB，若= a , = b , = 1 ，‎ ‎= 2, 则=( )‎ ‎（A）a + b （B）a +b （C）a +b （D）a +b ‎11、与正方体ABCD—A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点( )‎ ‎（A）有且只有1个 （B）有且只有2个 ‎（C）有且只有3个 （D）有无数个 ‎12、已知椭圆C：（a>b>0）的离心率为，过右焦点F且斜率为k（k>0）的直线于C相交于A、B两点，若。则k =( )‎ ‎（A）1 （B） （C） （D）2‎ 二．填空题 ‎13、已知α是第二象限的角,tanα=1/2，则cosα=__________‎ ‎14、(x+1/x)9的展开式中，x3的系数是_________‎ ‎15、已知抛物线C：y2=2px（p>0）的准线l，过M（1,0）且斜率为的直线与l相交于A，与C的一个交点为B，若，则p=_________‎ ‎16、已知球的半径为4，圆与圆为该球的两个小圆，为圆与圆的公共弦，，若，则两圆圆心的距离 。‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤。‎ ‎17、中，为边上的一点，，，，求。‎ ‎18、已知是各项均为正数的等比数列，且，‎ ‎（Ⅰ）求的通项公式； （Ⅱ）设，求数列的前项和。‎ ‎19、如图，直三棱柱ABC-ABC 中，AC=BC， AA=AB，D为BB的中点，E为AB上的一点，AE=3 EB ‎（Ⅰ）证明：DE为异面直线AB与CD的公垂线；‎ ‎（Ⅱ）设异面直线AB与CD的夹角为45°,求二面角A-AC-B的大小 ‎20、如图，由M到N的电路中有4个元件，分别标为T，T，T，T，电源能通过T，T，T的概率都是P，电源能通过T的概率是0.9，电源能否通过各元件相互独立。已知T，T，T中至少有一个能通过电流的概率为0.999。‎ ‎（Ⅰ）求P； （Ⅱ）求电流能在M与N之间通过的概率。‎ ‎21、 已知函数f（x）=x-3ax+3x+1。‎ ‎（Ⅰ）设a=2，求f（x）的单调期间；‎ ‎（Ⅱ）设f（x）在区间（2,3）中至少有一个极值点，求a的取值范围。‎ ‎22、已知斜率为1的直线1与双曲线C：相交于B、D两点，且BD的中点为M（1.3）‎ ‎（Ⅰ）（Ⅰ）求C的离心率；‎ ‎（Ⅱ）（Ⅱ）设C的右顶点为A，右焦点为F，|DF|·|BF|=17证明：过A、B、D三点的圆与x轴相切。‎ ‎（大纲卷）2011年高考文科数学试题 一、选择题 ‎（1）设集合U=,则( )‎ ‎（A） （B） （C） （D）‎ ‎（2）函数的反函数为( )‎ ‎（A） （B） （C） （D）‎ ‎（3）设向量a,b满足|a|=|b|=1,则( )‎ ‎（A） （B） （C） （D）‎ ‎（4）若变量x，y满足约束条件，则的最小值为( )‎ ‎（A）17 （B）14 （C）5 （D）3‎ ‎（5）下面四个条件中，使a>b成立的充分而不必要的条件是( )‎ ‎ (A) (B) (C) a2> b2 (D) a3> b3‎ ‎ (6) 设Sn为等差数列的前n项和，若，公差d=2，,则k=( )‎ ‎ (A)8 (B)7 (C) 6 (D) 5‎ ‎（7）设函数，将的图像向右平移个单位长度后，所得的图像与原图像重合，则的最小值等于( )‎ ‎（A） （B） （C） （D）‎ ‎ (8) 已知直二面角α- l –β，点A∈α，AC⊥l,C为垂足，点B∈β，BD⊥l,D为垂足.若AB=2，AC=BD=1，则CD=( )‎ ‎ （A） 2 （B） （C） （D）1‎ ‎(9)4位同学每人从甲、乙、丙3门课程中选修1门，则恰有2人选修课程甲的不同选法共有( )‎ ‎(A) 12种 (B) 24种 (C) 30种 (D)36种 ‎(10)设是周期为2的奇函数，当0≤x≤1时，=，则=( )‎ ‎ (A) - (B) (C) (D)‎ ‎(11)设两圆、都和两坐标轴相切，且都过点（4，1），则两圆心的距离=( )‎ ‎ (A)4 (B) (C)8 (D) ‎ ‎ (12)已知平面截一球面得圆M ， 过圆心M且与成，二面角的平面截该球面得圆N.若该球的半径为4，圆M的面积为4，则圆N的面积为( )‎ ‎ (A) (B) (c) (D)‎ ‎ ‎ 二、填空题 ‎(13)(1-)20的二项展开式中，x的系数与x9的系数之差为 .‎ ‎(14)已知a∈(，)，tanα=2，则cos2α= .‎ ‎（15）已知正方体ABCD-A1B‎1C1D1中，E为C1D1的中点，则异面直线AE与BC所成角的余弦值 为 .‎ ‎(16)已知F1、F2分别为双曲线C: - =1的左、右焦点，点A∈C，点M的坐标为(2，0)，AM为∠F1AF2的平分线．则|AF2| = .‎ 三．解答题：解答应写出文字说明，证明过程或演算步骤 ‎(17)设等比数列的前n项和为,已知求和.‎ ‎（18）△ABC的内角A、B、C的对边分别为a、b、c.己知.‎ ‎ (Ⅰ)求B； （Ⅱ）若.‎ ‎ (19)根据以往统计资料，某地车主购买甲种保险的概率为0.5，购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.‎ ‎ (I)求该地1位车主至少购买甲、乙两种保险中的1种的概率；‎ ‎（Ⅱ）求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.‎ ‎（20）如图,四棱锥S-ABCD中，AB//CD，BCCD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1‎ ‎（1）证明：SD平面SAB （2）求AB与平面SBC所成角的大小．‎ ‎（21）已知函数 ‎(Ⅰ)证明：曲线 ‎（Ⅱ）若求a的取值范围。‎ ‎（22）已知O为坐标原点，F为椭圆C：在y轴正半轴上的焦点，过F且斜率为的直线与C交与A，B两点，点P满足 (1) 证明：点P在C上；‎ (2) 设点P关于O的对称点为Q，证明：A、P、B、Q四点在同一个圆上．‎ ‎（大纲卷）2012年高考文科数学试题 一、 选择题 ‎（1）已知集合是平行四边形，是矩形，是正方形，是菱形，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（2）函数的反函数为（ ）‎ ‎（A） （B） ‎ ‎（C） （D）‎ ‎（3）若函数是偶函数，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（4）已知为第二象限角，，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（5）椭圆的中心在原点，焦距为，一条准线为，则该椭圆的方程为（ ）‎ ‎（A） （B） （C） （D）‎ ‎（6）已知数列的前项和为，，，,则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（7）位选手依次演讲，其中选手甲不再第一个也不再最后一个演讲，则不同的演讲次序共有（ ）‎ ‎（A）种 （B）种 （C）种 （D）种 ‎（8）已知正四棱柱中 ，，，为的中点，则直线与平面的距离为（ ）‎ ‎（A） （B） （C） （D）‎ ‎（9）中，边的高为，若，，，，，则（ ）‎ ‎（A） （B） （C） （D） ‎ ‎（10）已知、为双曲线的左、右焦点，点在上，，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（11）已知，，，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（12）正方形的边长为，点在边上，点在边上，。动点从出发沿直线向运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点第一次碰到时，与正方形的边碰撞的次数为（ ）‎ ‎（A） （B） （C） （D）‎ 二.填空题：‎ ‎（13）的展开式中的系数为____________.‎ ‎（14）若满足约束条件，则的最小值为____________.‎ ‎（15）当函数取得最大值时，___________.‎ ‎（16）已知正方体中，、分别为的中点，那么异面直线 与所成角的余弦值为____________.‎ 三． 解答题：解答应写出文字说明，证明过程或演算步骤 ‎（17）中，内角、、成等差数列，其对边、、满足，求。‎ ‎（18）已知数列中， ，前项和。‎ ‎（Ⅰ）求，； （Ⅱ）求的通项公式。‎ ‎（19）如图，四棱锥中，底面为菱形，底面，，，是上的一点，。‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）设二面角为，求与平面所成角的大小。‎ ‎（20）乒乓球比赛规则规定：一局比赛，双方比分在平前，一方连续发球次后，对方再连续发球次，依次轮换。每次发球，胜方得分，负方得分。设在甲、乙的比赛中，每次发球，发球方得分的概率为，各次发球的胜负结果相互独立。甲、乙的一局比赛中，甲先发球。‎ ‎（Ⅰ）求开始第次发球时，甲、乙的比分为比的概率；‎ ‎（Ⅱ）求开始第次发球时，甲得分领先的概率。‎ ‎（21）已知函数 ‎（Ⅰ）讨论的单调性；‎ ‎（Ⅱ）设有两个极值点，若过两点，的直线与轴的交点在曲线上，求的值。‎ ‎（22）已知抛物线与圆有一个公共点，且在点处两曲线的切线为同一直线.‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）设、是异于且与及都相切的两条直线，、的交点为，求到的距离。‎