新课标2008-2011全国高考各省市文科数学分类汇编——概率与统计精校版 23页

新课标2008-2011全国高考各省市文科数学分类汇编——概率与统计（精校版）‎ 概率部分 ‎1. （2009福建卷文）（本小题满分12分）‎ 袋中有大小、形状相同的红、黑球各一个，现一次有放回地随机摸取3次，每次摸取一个球 ‎ （I）试问：一共有多少种不同的结果？请列出所有可能的结果； ‎ ‎ （Ⅱ）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率。‎ 解：（I）一共有8种不同的结果，列举如下：‎ ‎ （红、红、红、）、（红、红、黑）、（红、黑、红）、（红、黑、黑）、（黑、红、红）、（黑、红、黑）、（黑、黑、红）、（黑、黑、黑）‎ ‎ （Ⅱ）记“3次摸球所得总分为‎5”‎为事件A ‎ 事件A包含的基本事件为：（红、红、黑）、（红、黑、红）、（黑、红、红）事件A包含的基本事件数为3‎ ‎ 由（I）可知，基本事件总数为8，所以事件A的概率为 w.w.‎ ‎2. （2009天津卷文）（本小题满分12分）‎ 为了了解某工厂开展群众体育活动的情况，拟采用分层抽样的方法从A，B,C三个区中抽取7个工厂进行调查，已知A,B，C区中分别有18，27，18个工厂 ‎（Ⅰ）求从A,B,C区中分别抽取的工厂个数；‎ ‎（Ⅱ）若从抽取的7个工厂中随机抽取2个进行调查结果的对比，用列举法计算这2个工厂中至少有1个来自A区的概率。‎ ‎【答案】(1) 2，3，2(2) ‎ ‎【解析】 （1）解： 工厂总数为18+27+18=63，样本容量与总体中的个体数比为，所以从A,B,C三个区中应分别抽取的工厂个数为2，3，2.‎ ‎（2）设为在A区中抽得的2个工厂，为在B区中抽得的3个工厂，为在C区中抽得的2个工厂，这7个工厂中随机的抽取2个，全部的可能结果有：种，随机的抽取的2个工厂至少有一个来自A区的结果有，,同理还能组合5种，一共有11种。所以所求的概率为 ‎【考点定位】本小题主要考查分层抽样、用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查运用统计、概率知识解决实际问题的能力。‎ ‎3.(2009山东卷文)（本小题满分12分）‎ ‎ 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):‎ 轿车A 轿车B 轿车C 舒适型 ‎100‎ ‎150‎ z 标准型 ‎300‎ ‎450‎ ‎600‎ 按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.‎ （1） 求z的值. ‎ （2） 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;‎ （3） 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.‎ 解: (1).设该厂本月生产轿车为n辆,由题意得,,所以n=2000. z=2000-100-300-150-450-600=400‎ ‎(2) 设所抽样本中有m辆舒适型轿车,因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,所以,解得m=2也就是抽取了2辆舒适型轿车,3辆标准型轿车,分别记作S1,S2;B1,B2,B3,则从中任取2辆的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1辆舒适型轿车的基本事件有7个基本事件: (S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2辆,至少有1辆舒适型轿车的概率为.‎ ‎(3)样本的平均数为,‎ 那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为.‎ ‎【命题立意】:本题为概率与统计的知识内容,涉及到分层抽样以及古典概型求事件的概率问题.要读懂题意,分清类型,列出基本事件,查清个数.,利用公式解答.‎ ‎4（2010湖南文数）17. （本小题满分12分）‎ 为了对某课题进行研究，用分层抽样方法从三所高校A,B,C的相关人员中，抽取若干人组成研究小组、有关数据见下表（单位：人）‎ ‎（Ⅰ）求x,y ;‎ ‎(Ⅱ)若从高校B、C抽取的人中选2人作专题发言，求这二人都来自高校C的概率。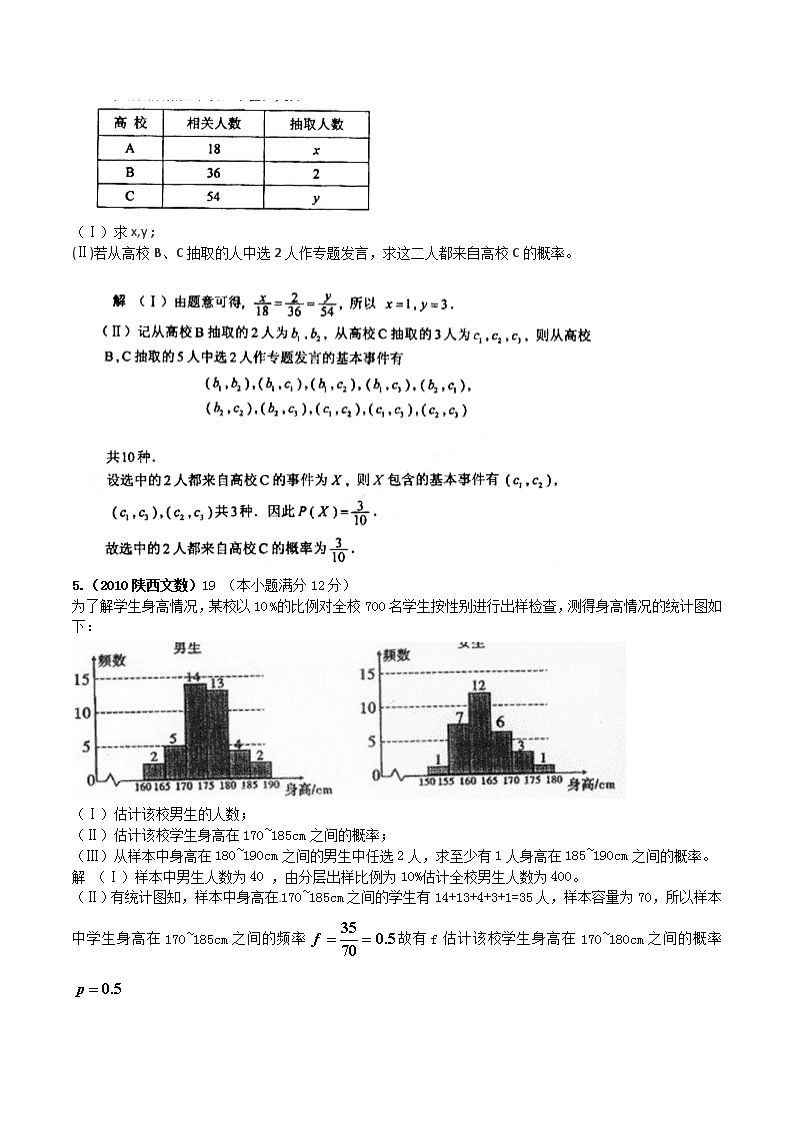‎ ‎5.（2010陕西文数）19 （本小题满分12分）‎ 为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行出样检查，测得身高情况的统计图如下：‎ ‎（Ⅰ）估计该校男生的人数；‎ ‎（Ⅱ）估计该校学生身高在170~‎185cm之间的概率；‎ ‎（Ⅲ）从样本中身高在180~‎190cm之间的男生中任选2人，求至少有1人身高在185~‎190cm之间的概率。‎ 解 （Ⅰ）样本中男生人数为40 ，由分层出样比例为10%估计全校男生人数为400。‎ ‎（Ⅱ）有统计图知，样本中身高在170~‎185cm之间的学生有14+13+4+3+1=35人，样本容量为70 ，所以样本中学生身高在170~‎185cm之间的频率故有f估计该校学生身高在170~‎180cm之间的概率 ‎（Ⅲ）样本中身高在180~‎185cm之间的男生有4人，设其编号为①②③④‎ ‎ 样本中身高在185~‎190cm之间的男生有2人，设其编号为⑤⑥‎ 从上述6人中任取2人的树状图为：‎ 故从样本中身高在180~‎190cm之间的男生中任选2人得所有可能结果数为15，求至少有1人身高在185~‎190cm之间的可能结果数为9，因此，所求概率 ‎6.（2010山东文数）（19）（本小题满分12分）‎ ‎ 一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4.‎ ‎（Ⅰ）从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；‎ ‎（Ⅱ）先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，求的概率.‎ ‎7.（2010天津文数）（18）（本小题满分12分）‎ 有编号为,,…的10个零件，测量其直径（单位：cm），得到下面数据：‎ 其中直径在区间[1.48，1.52]内的零件为一等品 编号 直径 ‎1.51‎ ‎1.49‎ ‎1.49‎ ‎1.51‎ ‎1.49‎ ‎1.51‎ ‎1.47‎ ‎1.46‎ ‎1.53‎ ‎1.47‎ ‎（Ⅰ）从上述10个零件中，随机抽取一个，求这个零件为一等品的概率；‎ ‎（Ⅱ）从一等品零件中，随机抽取2个.‎ ‎ （ⅰ）用零件的编号列出所有可能的抽取结果；‎ ‎ （ⅱ）求这2个零件直径相等的概率。本小题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力。满分12分 ‎ 【解析】（Ⅰ）解：由所给数据可知，一等品零件共有6个.设“从10个零件中，随机抽取一个为一等品”为事件A，则P（A）==.‎ ‎ （Ⅱ）（i）解：一等品零件的编号为.从这6个一等品零件中随机抽取2个，所有可能的结果有：,,,‎ ‎,,,共有15种.‎ ‎ (ii)解：“从一等品零件中，随机抽取的2个零件直径相等”（记为事件B）的所有可能结果有：，，共有6种.‎ ‎ 所以P(B)=.‎ ‎8. 2011．（天津文）15．（本小题满分13分）‎ ‎ 编号为的16名篮球运动员在某次训练比赛中的得分记录如下：‎ 运动员编号 得分 ‎15‎ ‎35‎ ‎21‎ ‎28‎ ‎25‎ ‎36‎ ‎18‎ ‎34‎ 运动员编号 得分 ‎17‎ ‎26‎ ‎25‎ ‎33‎ ‎22‎ ‎12‎ ‎31‎ ‎38‎ ‎（Ⅰ）将得分在对应区间内的人数填入相应的空格；‎ 区间 人数 ‎（Ⅱ）从得分在区间内的运动员中随机抽取2人，‎ ‎（i）用运动员的编号列出所有可能的抽取结果；‎ ‎（ii）求这2人得分之和大于50的概率．‎ ‎ ‎ ‎【解析】（15）本小题主要考查用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式的等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力，满分13分。‎ ‎ （Ⅰ）解：4，6，6‎ ‎ （Ⅱ）（i）解：得分在区间内的运动员编号为从中随机抽取2人，所有可能的抽取结果有：‎ ‎，‎ ‎ ，共15种。‎ ‎ （ii）解：“从得分在区间内的运动员中随机抽取2人，这2人得分之和大于‎50”‎（记为事件B）的所有可能结果有：，共5种。‎ ‎ 所以 ‎9. 2011. （北京文）16．（本小题共13分）‎ ‎ 以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊，无法确认，在图中以X表示.‎ ‎ （1）如果X=8，求乙组同学植树棵树的平均数和方差；‎ ‎（2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.‎ ‎ （注：方差其中为的平均数）‎ ‎【解析】（16）（共13分）‎ 解（1）当X=8时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10，‎ 所以平均数为 方差为 ‎（Ⅱ）记甲组四名同学为A1，A2，A3，A4，他们植树的棵数依次为9，9，11，11；乙组四名同学为B1，B2，B3，B4，他们植树的棵数依次为9，8，9，10，分别从甲、乙两组中随机选取一名同学，所有可能的结果有16个，它们是：‎ ‎ （A1，B1），（A1，B2），（A1，B3），（A1，B4），‎ ‎ （A2，B1），（A2，B2），（A2，B3），（A2，B4），‎ ‎ （A3，B1），（A2，B2），（A3，B3），（A1，B4），‎ ‎ （A4，B1），（A4，B2），（A4，B3），（A4，B4），‎ ‎ 用C表示：“选出的两名同学的植树总棵数为19”这一事件，则C中的结果有4个，它们是：（A1，B4），（A2，B4），（A3，B2），（A4，B2），故所求概率为 ‎10. （江西文）16．（本小题满分12分）‎ 某饮料公司对一名员工进行测试以便确定考评级别，公司准备了两种不同的饮料共5杯，其颜色完全相同，并且其中的3杯为A饮料，另外的2杯为B饮料，公司要求此员工一一品尝后，从5杯饮料中选出3杯A饮料。若该员工3杯都选对，测评为优秀；若3杯选对2杯测评为良好；否测评为合格。假设此人对A和B两种饮料没有鉴别能力 ‎（1）求此人被评为优秀的概率 ‎（2）求此人被评为良好及以上的概率 ‎【解析】16．（本小题满分12分）‎ ‎ 解：将5不饮料编号为：1，2，3，4，5，编号1，2，3表示A饮料，编号4，5表示B饮料，则从5‎ 杯饮料中选出3杯的所有可能情况为：（123），（124），（1，2，5），（134），（135），（145），（234），（235），（245），（345）可见共有10种 ‎ 令D表示此人被评为优秀的事件，E表示此人被评人良好的事件，F表示此人被评为良好及以上的事件。则 ‎ （1）‎ ‎ （2）‎ ‎11. （山东文）18．（本小题满分12分）‎ 甲、乙两校各有3名教师报名支教，其中甲校2男1女，乙校1男2女．‎ ‎（I）若从甲校和乙校报名的教师中各任选1名，写出所有可能的结果，并求选出的2名教师性别相同的概率；‎ ‎（II）若从报名的6名教师中任选2名，写出所有可能的结果，并求选出的2名教师来自同一学校的概率．‎ ‎【解析】18．解：（I）甲校两男教师分别用A、B表示，女教师用C表示；‎ 乙校男教师用D表示，两女教师分别用E、F表示 从甲校和乙校报名的教师中各任选1名的所有可能的结果为：‎ ‎（A，D）（A，E），（A，F），（B，D），（B，E），（B，F），（C，D），（C，E），（C，F）共9种。‎ 从中选出两名教师性别相同的结果有：（A，D），（B，D），（C，E），（C，F）共4种，‎ 选出的两名教师性别相同的概率为 ‎ （II）从甲校和乙校报名的教师中任选2名的所有可能的结果为：‎ ‎（A，B），（A，C），（A，D），（A，E），（A，F），（B，C），（B，D），（B，E），（B，F），‎ ‎（C，D），（C，E），（C，F），（D，E），（D，F），（E，F）共15种，‎ 从中选出两名教师来自同一学校的结果有：‎ ‎（A，B），（A，C），（B，C），（D，E），（D，F），（E，F）共6种，‎ 选出的两名教师来自同一学校的概率为 ‎12. （陕西文）20．（本小题满分13分）‎ 如图，A地到火车站共有两条路径L1和L2，现随机抽取100位从A地到火车站的人进行调查，调查结果如下：‎ 所用时间（分钟）‎ ‎10~20‎ ‎20~30‎ ‎30~40‎ ‎40~50‎ ‎50~60‎ 选择L1的人数 ‎6‎ ‎12‎ ‎18‎ ‎12‎ ‎12‎ 选择L2的人数 ‎0‎ ‎4‎ ‎16‎ ‎16‎ ‎4‎ ‎（Ⅰ）试估计40分钟内不能赶到火车站的概率;‎ ‎（Ⅱ）分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;‎ ‎（Ⅲ）现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站，为了尽量大可能在允许的时间内赶到火车站，试通过计算说明，他们应如何选择各自的 路径。‎ ‎【解析】20．解（Ⅰ）由已知共调查了100人，其中40分钟内不能赶到火车站的有12+12+16+4=44人，‎ 用频率估计相应的概率为0．44．‎ ‎（Ⅱ ）选择L1的有60人，选择L2的有40人，‎ 故由调查结果得频率为：‎ 所用时间（分钟）‎ ‎10~20‎ ‎20~30‎ ‎30~40‎ ‎40~50‎ ‎50~60‎ L1的频率 ‎0．1‎ ‎0．2‎ ‎0．3‎ ‎0．2‎ ‎0．2‎ L2的频率 ‎0‎ ‎0．1‎ ‎0．4‎ ‎0．4‎ ‎0．1‎ ‎（Ⅲ）A1，A2，分别表示甲选择L1和L2时，在40分钟内赶到火车站；‎ B1，B2分别表示乙选择L1和L2时，在50分钟内赶到火车站。‎ 由（Ⅱ）知P（A1） =0.1+0.2+0.3=0.6‎ P（A2）=0.1+0.4=0.5， P（A1）>P（A2）‎ 甲应选择L1‎ P（B1） =0.1+0.2+0.3+0.2=0.8‎ P（B2）=0.1+0.4+0.4=0.9，P（B2）＞P（B1），‎ ‎∴ 乙应选择L2．‎ ‎13. （福建文）19．（本小题满分12分）‎ 某日用品按行业质量标准分成五个等级，等级系数X依次为1．2．3．4．5．现从一批该日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如下：‎ X ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ f a ‎0．2‎ ‎0．45‎ b C ‎ （I）若所抽取的20件日用品中，等级系数为4的恰有4件，等级系数为5的恰有2件，求a、b、c的值；‎ ‎（11）在（1）的条件下，将等级系数为4的3件日用品记为x1,x2,x3，等级系数为5的2件日用品记为y1,y2，现从x1,x2,x3,y1,y2,这5件日用品中任取两件（假定每件日用品被取出的可能性相同），写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率。‎ ‎【解析】19．本小题主要考查概率、统计等基础知识，考查数据处理能力、运算求解能力、应用意识，考查函数与方程思想、分类与整合思想、必然与或然思想，满分12分。‎ ‎ 解：（I）由频率分布表得，‎ 因为抽取的20件日用品中，等级系数为4的恰有3件，‎ 所以 等级系数为5的恰有2件，所以，‎ 从而 所以 ‎（II）从日用品中任取两件，‎ 所有可能的结果为：‎ ‎，‎ 设事件A表示“从日用品中任取两件，其等级系数相等”，则A包含的基本事件为：‎ 共4个，‎ 又基本事件的总数为10，‎ 故所求的概率 ‎14. （2011广东文）17．（本小题满分13分）‎ ‎ 在某次测验中，有6位同学的平均成绩为75分。用xn表示编号为n（n=1,2,…,6）的同学所得成绩，且前5位同学的成绩如下：‎ 编号n ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 成绩xn ‎70‎ ‎76‎ ‎72‎ ‎70‎ ‎72‎ ‎（1）求第6位同学的成绩x6，及这6位同学成绩的标准差s;‎ ‎（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率。‎ ‎【解析】17．（本小题满分13分）‎ ‎ 解：（1）‎ ‎ ‎ ‎ ，‎ ‎ ‎ ‎ （2）从5位同学中随机选取2位同学，共有如下10种不同的取法：‎ ‎ {1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}，{3，4}，{3，5}，{4，5}，‎ ‎ 选出的2位同学中，恰有1位同学的成绩位于（68，75）的取法共有如下4种取法：‎ ‎ {1，2}，{2，3}，{2，4}，{2，5}，‎ ‎ 故所求概率为 ‎15．（本小题满分12分）‎ 现有8名奥运会志愿者，其中志愿者通晓日语，通晓俄语，通晓韩语．从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组．‎ ‎（Ⅰ）求被选中的概率；‎ ‎（Ⅱ）求和不全被选中的概率．‎ ‎18．解：（Ⅰ）从8人中选出日语、俄语和韩语志愿者各1名，其一切可能的结果组成的基本事件空间 ‎{，，‎ ‎，，，‎ ‎，，，‎ ‎}‎ 由18个基本事件组成．由于每一个基本事件被抽取的机会均等，因此这些基本事件的发生是等可能的．‎ 用表示“恰被选中”这一事件，则 ‎{，‎ ‎}‎ 事件由6个基本事件组成，‎ 因而．‎ ‎（Ⅱ）用表示“不全被选中”这一事件，则其对立事件表示“全被选中”这一事件，‎ 由于{}，事件有3个基本事件组成，‎ 所以，由对立事件的概率公式得．‎ ‎16、（本小题满分12分）为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查，6人得分情况如下：5，6，7，8，9，10。把这6名学生的得分看成一个总体。（1）求该总体的平均数；（2）用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本。求该样本平均数与总体平均数之差的绝对值不超过0.5的概率。‎ ‎19．解：‎ ‎（Ⅰ）总体平均数为 ‎． 4分 ‎（Ⅱ）设表示事件“样本平均数与总体平均数之差的绝对值不超过‎0.5”‎．‎ 从总体中抽取2个个体全部可能的基本结果有：，，，，，，，，，，，，，，．共15个基本结果．‎ 事件包括的基本结果有：，，，，，，．共有7个基本结果．‎ 所以所求的概率为 ‎． 12分 统计部分 ‎1.（2009宁夏海南卷文）（本小题满分12分）‎ ‎ 某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人）.现用分层抽样方法（按A类，B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）.‎ ‎（Ⅰ）A类工人中和B类工人各抽查多少工人？w.w.w.k.s.5.u.c.o.m ‎ ‎（Ⅱ）从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2‎ 表1：‎ 生产能力分组 人数 ‎4‎ ‎8‎ ‎5‎ ‎3‎ 表2：‎ 生产能力分组 人数 ‎ 6‎ ‎ y ‎ 36‎ ‎ 18‎ （1） 先确定，再在答题纸上完成下列频率分布直方图。就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）‎ ‎(ii)分别估计类工人和类工人生产能力的平均数，并估计该工厂工人和生产能力的平均数（同一组中的数据用该区间的中点值作代表）。‎ ‎（19）解：‎ ‎（Ⅰ）类工人中和类工人中分别抽查25名和75名。 ．．．．．．4分 ‎（Ⅱ）(ⅰ)由，得，‎ ‎ ，得。 ‎ 频率分布直方图如下 ‎ ．．．．．．8分 从直方图可以判断：类工人中个体间的差异程度更小。 ．．．．．．9分 ‎ （ii） ，‎ ‎ ， ‎ ‎ ‎ A类工人生产能力的平均数，B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123，133.8和131.1.‎ 统计题型 ‎2.(2009年广东卷文)（本小题满分13分）‎ 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.‎ ‎(1)根据茎叶图判断哪个班的平均身高较高;‎ ‎(2)计算甲班的样本方差 ‎(3)现从乙班这10名同学中随机抽取两名身高不低于‎173cm的同学,求身高为‎176cm的同学被抽中的概率.‎ ‎【解析】（1）由茎叶图可知：甲班身高集中于之间，而乙班身高集中于 之间。因此乙班平均身高高于甲班;‎ ‎ (2) ‎ ‎ 甲班的样本方差为 ‎ ＝57‎ ‎ （3）设身高为‎176cm的同学被抽中的事件为A；‎ ‎ 从乙班10名同学中抽中两名身高不低于‎173cm的同学有：（181，173） （181，176）‎ ‎ （181，178） （181，179） （179，173） （179，176） （179，178） （178，173）‎ ‎ (178, 176) （176，173）共10个基本事件，而事件A含有4个基本事件；‎ ‎ ；‎ ‎3.（2009安徽卷文）（本小题满分12分）‎ ‎ 某良种培育基地正在培育一种小麦新品种A，将其与原有的一个优良品种B进行对照 试验，两种小麦各种植了25亩，所得亩产数据（单位：千克）如下：w.w.w.k.s.5.u.c.o.m ‎ 品种A:357，359，367，368，375，388，392，399，400，405，414，‎ ‎ 415，421，423，423，427，430，430，434，443，445，451，454‎ 品种B：363，371，374，383，385，386，391，392，394，395，397‎ ‎ 397，400，401，401，403，406，407，410，412，415，416，422，430‎ ‎（Ⅰ）完成所附的茎叶图 ‎（Ⅱ）用茎叶图处理现有的数据，有什么优点？w.w.w.k.s.5.u.c.o.m ‎ ‎（Ⅲ）通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论。‎ ‎【思路】由统计知识可求出A、B两种品种的小麦稳定性大小并画出茎叶图，用茎叶图处理数据，看其分布就比较明了。w.w.w.k.s.5.u.c.o.m ‎ ‎【解析】（1）茎叶图如图所示 A B ‎9 7‎ ‎35‎ ‎8 7‎ ‎36‎ ‎3‎ ‎5‎ ‎37‎ ‎1 4‎ ‎8‎ ‎38‎ ‎3 5 6‎ ‎9 2‎ ‎39‎ ‎1 2 4 457 7‎ ‎5 0‎ ‎40‎ ‎0 1 1 3 6 7‎ ‎5 4 2‎ ‎41‎ ‎0 2 5 6‎ ‎7 3 3 1‎ ‎42‎ ‎2‎ ‎4 0 0‎ ‎43‎ ‎0‎ ‎5 5 3‎ ‎44‎ ‎4 1‎ ‎45‎ ‎（2）用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.‎ ‎（3）通过观察茎叶图，可以发现品种A的平均每亩产量为411.1千克，品种B的平均亩产量为397.8千克.由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定，而品种B的亩产量比较集中D平均产量附近 ‎4.（2009辽宁卷文）（本小题满分12分）‎ ‎ 某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在（29.94，30.06）的零件为优质品。从两个分厂生产的零件中个抽出500件，量其内径尺寸，的结果如下表：‎ ‎ 甲厂 （1） 试分别估计两个分厂生产的零件的优质品率；‎ （2） 由于以上统计数据填下面列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。‎ 甲 厂 ‎ 乙 厂 ‎ 合计 优质品 ‎ 非优质品 ‎ 合计 附：‎ 解：‎ ‎（Ⅰ）甲厂抽查的产品中有360件优质品，从而甲厂生产的零件的优质品率估计为； ……6分 乙厂抽查的产品中有320件优质品，从而乙厂生产的零件的优质品率估计为 ‎（Ⅱ）‎ ‎ ‎ 甲厂 乙厂 合计 优质品 ‎360‎ ‎320‎ ‎680‎ 非优质品 ‎140‎ ‎180‎ ‎320‎ 合计 ‎500‎ ‎500‎ ‎1000‎ ‎ ……8分 ‎ ‎ 所以有99%的把握认为“两个分厂生产的零件的质量有差异”。 ……12分 ‎5.（2010广东文数）17.（本小题满分12分）‎ 某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：‎ 文艺节目 新闻节目 总计 ‎20至40岁 ‎40‎ ‎18‎ ‎58‎ 大于40岁 ‎15‎ ‎27‎ ‎42‎ 总计 ‎55‎ ‎45‎ ‎100‎ ‎6.（2010辽宁文数）（18）（本小题满分12分）‎ 为了比较注射A,B两种药物后产生的皮肤疱疹的面积，选200只家兔做实验，将这200只家兔随机地分成两组。每组100只，其中一组注射药物A，另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。（疱疹面积单位：）‎ ‎（Ⅰ）完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；‎ ‎（Ⅱ）完成下面列联表，并回答能否有99.9％的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 K^S*5U.C#‎ 附： ‎ 解：‎ ‎ （Ⅰ）‎ 图1注射药物A后皮肤疱疹面积的频率分布直方图 图2注射药物B后皮肤疱疹面积的频率分布直方图 ‎ 可以看出注射药物A后的疱疹面积的中位数在65至70之间，而注射药物B后的疱疹面积的中位数在70至75之间，所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数。‎ ‎ （Ⅱ）表3‎ 疱疹面积小于 疱疹面积不小于 合计 注射药物 注射药物 合计 ‎ ‎ ‎ 由于，所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.‎ ‎7.（2010安徽文数）18、（本小题满分13分）‎ ‎ 某市‎2010年4月1日—‎4月30日对空气污染指数的监测数据如下（主要污染物为可吸入颗粒物）:‎ ‎ 61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,‎ ‎ 77,86,81,83,82,82,64,79,86,85,75,71,49,45,‎ ‎(Ⅰ) 完成频率分布表；‎ ‎（Ⅱ）作出频率分布直方图；‎ ‎（Ⅲ）根据国家标准，污染指数在0~50之间时，空气质量为优：在51~100之间时，为良；在101~150‎ 之间时，为轻微污染；在151~200之间时，为轻度污染。‎ 请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价.‎ ‎【命题意图】本题考查频数，频率及频率分布直方图，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识. ‎ ‎【解题指导】（1）首先根据题目中的数据完成频率分布表，作出频率分布直方图，根据污染指数，确定空气质量为优、良、轻微污染、轻度污染的天数。‎ ‎(Ⅲ)答对下述两条中的一条即可：‎ （1） 该市一个月中空气污染指数有2天处于优的水平，占当月天数的，有26天处于良的水平，占当月天数的，处于优或良的天数共有28天，占当月天数的。说明该市空气质量基本良好。‎ （2） 轻微污染有2天，占当月天数的。污染指数在80以上的接近轻微污染的天数有15天，加上处于轻微污染的天数，共有17天，占当月天数的，超过50%，说明该市空气质量有待进一步改善。‎ ‎【规律总结】在频率分布表中，频数的和等于样本容量，频率的和等于1，每一小组的频率等于这一组的频数除以样本容量.频率分布直方图中，小矩形的高等于每一组的频率/组距，它们与频数成正比，小矩形的面积等于这一组的频率.对于开放性问题的回答，要选择适当的数据特征进行考察，根据数据特征分析得出实际问题的结论.‎ ‎8.（2010全国新课标19）（本小题满分12分）‎ 为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如下：‎ ‎ 性别 您是否需要志愿者 男 女 需要 ‎40‎ ‎30‎ 不需要 ‎160‎ ‎270‎ ‎（Ⅰ）估计该地区老年人中，需要志愿提供帮助的老年人的比例；‎ ‎（Ⅱ）能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？‎ ‎（Ⅲ）根据（Ⅱ）的结论，能否提出更好的调查办法来估计该地区的老年人中，需要志愿者提供帮助的老年人的比例？说明理由。‎ 附：‎ ‎ ‎ K2= 解：（1）调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中需要帮助的老年人的比例的估计值为. ……4分 ‎(2) ‎ 由于所以有99%的把握认为该地区的老年人是否需要帮助与性别有关. ……8分 ‎（3）由于（2）的结论知，该地区的老年人是否需要帮助与性别有关，并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男,女的比例，再把老年人分成男,女两层并采用分层抽样方法比采用简单反随即抽样方法更好. ……12分 ‎9. 2011. （全国新文）19．（本小题满分12分）‎ ‎ 某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每产品的质量指标值，得到时下面试验结果：‎ A配方的频数分布表 指标值分组 ‎[90，94）‎ ‎[94，98）‎ ‎[98，102）‎ ‎[102，106）‎ ‎[106，110]‎ 频数 ‎8‎ ‎20‎ ‎42‎ ‎22‎ ‎8‎ B配方的频数分布表 指标值分组 ‎[90，94）‎ ‎[94，98）‎ ‎[98，102）‎ ‎[102，106）‎ ‎[106，110]‎ 频数 ‎4‎ ‎12‎ ‎42‎ ‎32‎ ‎10‎ ‎ （I）分别估计用A配方，B配方生产的产品的优质品率；‎ ‎ （II）已知用B配方生产的一种产品利润y（单位：元）与其质量指标值t的关系式为 ‎ 估计用B配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述100件产品平均一件的利润．‎ ‎【解析】（19）解 ‎（Ⅰ）由试验结果知，用A配方生产的产品中优质的频率为，所以用A配方生产的产品的优质品率的估计值为0.3。‎ 由试验结果知，用B配方生产的产品中优质品的频率为，所以用B配方生产的产品的优质品率的估计值为0.42‎ ‎（Ⅱ）由条件知用B配方生产的一件产品的利润大于0当且仅当其质量指标值t≥94，由试验结果知，质量指标值t≥94的频率为0.96，所以用B配方生产的一件产品的利润大于0的概率估计值为0.96.‎ 用B配方生产的产品平均一件的利润为 ‎（元）‎ ‎10. （2011辽宁文）19．（本小题满分12分）‎ 某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙．‎ ‎（I）假设n=2，求第一大块地都种植品种甲的概率；‎ ‎（II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm2）如下表：‎ 品种甲 ‎403‎ ‎397‎ ‎390‎ ‎404‎ ‎388‎ ‎400‎ ‎412‎ ‎406‎ 品种乙 ‎419‎ ‎403‎ ‎412‎ ‎418‎ ‎408‎ ‎423‎ ‎400‎ ‎413‎ 分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？‎ 附：样本数据的的样本方差，其中为样本平均数．‎ ‎【解析】19．解：（I）设第一大块地中的两小块地编号为1，2，第二大块地中的两小块地编号为3，4，‎ 令事件A=“第一大块地都种品种甲”.‎ 从4小块地中任选2小块地种植品种甲的基本事件共6个；‎ ‎（1，2），（1，3），（1，4），（2，3），（2，4），（3，4）.‎ 而事件A包含1个基本事件：（1，2）.‎ 所以 ………………6分 ‎ （II）品种甲的每公顷产量的样本平均数和样本方差分别为：‎ ‎ ………………8分 品种乙的每公顷产量的样本平均数和样本方差分别为：‎ ‎ ………………10分 由以上结果可以看出，品种乙的样本平均数大于品种甲的样本平均数，且两品种的样本方差差异不大，故应该选择种植品种乙.‎ ‎11. （2011安徽文）（20）（本小题满分10分）‎ 某地最近十年粮食需求量逐年上升，下表是部分统计数据：‎ 年份 ‎2002‎ ‎2004‎ ‎2006‎ ‎2008‎ ‎2010‎ 需求量（万吨）‎ ‎236‎ ‎246‎ ‎257‎ ‎276‎ ‎286‎ ‎（Ⅰ）利用所给数据求年需求量与年份之间的回归直线方程;‎ ‎（Ⅱ）利用（Ⅰ）中所求出的直线方程预测该地2012年的粮食需求量。‎ 温馨提示：答题前请仔细阅读卷首所给的计算公式及说明.‎ ‎【解析】（20）（本小题满分10分）本题考查回归分析的基本思想及其初步应用，回归直线的意义和求法，数据处理的基本方法和能力，考查运用统计知识解决简单实际应用问题的能力.‎ ‎ 解：（I）由所给数据看出，年需求量与年份之间是近似直线上升，下面来配回归直线方程，为此对数据预处理如下：‎ 年份—2006‎ ‎－4‎ ‎－2‎ ‎0‎ ‎2‎ ‎4‎ 需求量—257‎ ‎－21‎ ‎－11‎ ‎0‎ ‎19‎ ‎29‎ 对预处理后的数据，容易算得 ‎ ‎ ‎ 由上述计算结果，知所求回归直线方程为 ‎ ‎ ‎ 即 ①‎ ‎ （II）利用直线方程①，可预测2012年的粮食需求量为 ‎ （万吨）≈300（万吨）.‎ ‎12. （2011湖南文）18．（本小题满分12分）‎ 某河流上的一座水力发电站，每年六月份的发电量Y（单位：万千瓦时）与该河上游在六月份是我降雨量X（单位：毫米）有关，据统计，当X=70时，Y=460；X每增加10，Y增加5．已知近20年X的值为：140, 110, 160, 70, 200, 160, 140, 160, 220, 200, 110, 160, 160, 200, 140, 110, 160, 220, 140, 160.‎ ‎ （Ⅰ）完成如下的频率分布表 近20年六月份降雨量频率分布表 降雨量 ‎70‎ ‎110‎ ‎140‎ ‎160‎ ‎200‎ ‎220‎ 频率 ‎ （Ⅱ）假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同，并将频率是为概率，求今年六月份该水力发电站的发电量低于490（万千瓦时）或超过530（万千瓦时）的概率．‎ ‎【解析】18．（本题满分12分）‎ 解：（I）在所给数据中，降雨量为110毫米的有3个，为160毫米的有7个，为200毫米的有3个，故近20年六月份降雨量频率分布表为 降雨量 ‎70‎ ‎110‎ ‎140‎ ‎160‎ ‎200‎ ‎220‎ 频率 ‎ （II）P（“发电量低于490万千瓦时或超过530万千瓦时”）‎ ‎ ‎ 故今年六月份该水力发电站的发电量低于490（万千瓦时）或超过530（万千瓦时）的概率为．‎ ‎13.（2009广东本小题满分13分）‎ 某初级中学共有学生2000名，各年级男、女生人数如下表：‎ 初一年级 初二年级 初三年级 女生 ‎373‎ x y 男生 ‎377‎ ‎370‎ z 已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.‎ （1） 求x的值；‎ （2） 现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？‎ （3） 已知y245,z245,求初三年级中女生比男生多的概率.‎ 解：（1）因为，所以 ‎ （2）初三年级人数为 ‎ 现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为 ‎ 名 ‎ （3）设初三年级女生比男生多的事件为,初三年级女生男生数记为 ‎ ，由（2）知，且 ‎ 基本事件共有共11个，‎ ‎ 事件包含的基本事件有 共5个，所以