高考抛物线专题做题技巧与方法总结 16页

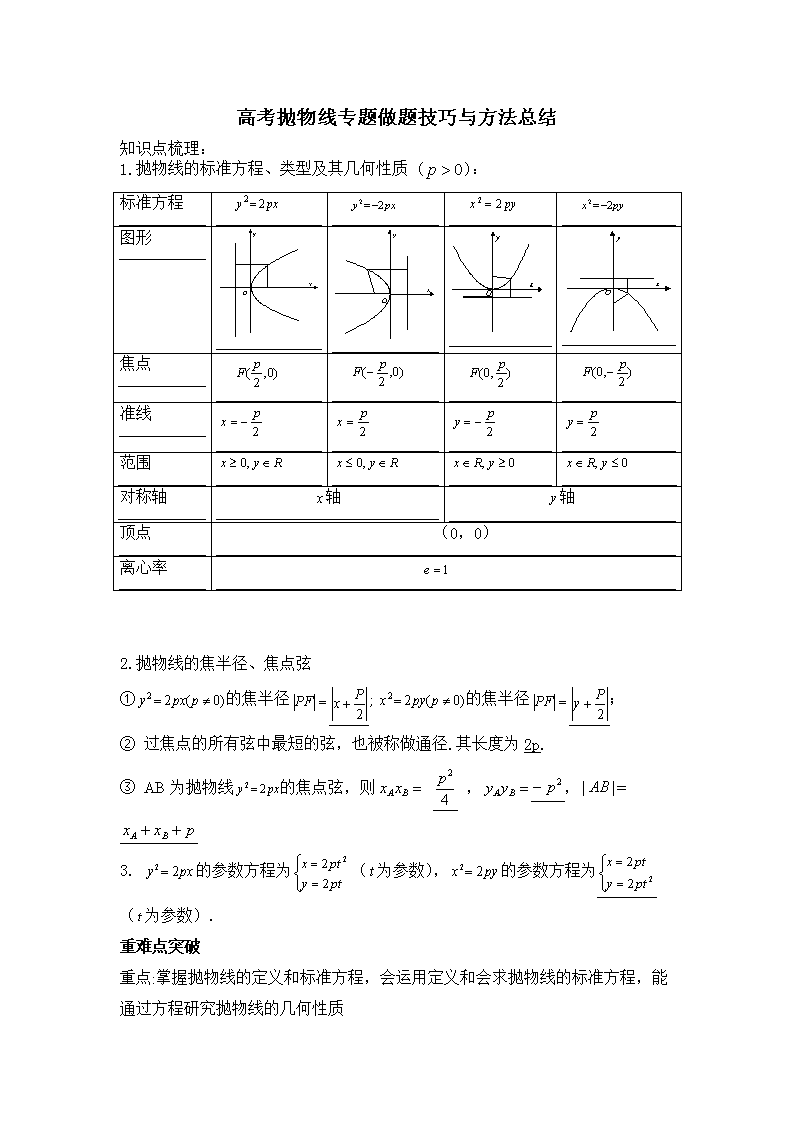
高考抛物线专题做题技巧与方法总结 知识点梳理：‎ ‎1.抛物线的标准方程、类型及其几何性质 ()：‎ 标准方程 图形 焦点 准线 范围 对称轴 轴 轴 顶点 ‎ （0，0）‎ 离心率 ‎2.抛物线的焦半径、焦点弦 ‎①的焦半径;的焦半径；‎ ‎② 过焦点的所有弦中最短的弦，也被称做通径.其长度为2p.‎ ‎③ AB为抛物线的焦点弦，则 ，，=‎ ‎3. 的参数方程为（为参数），的参数方程为（为参数）.‎ 重难点突破 重点:掌握抛物线的定义和标准方程，会运用定义和会求抛物线的标准方程，能通过方程研究抛物线的几何性质 难点: 与焦点有关的计算与论证 重难点:围绕焦半径、焦点弦，运用数形结合和代数方法研究抛物线的性质 ‎1.要有用定义的意识 问题1：抛物线y=4上的一点M到焦点的距离为1，则点M的纵坐标是( )‎ ‎ A. B. C. D. 0‎ 点拨：抛物线的标准方程为，准线方程为,由定义知，点M到准线的距离为1，所以点M的纵坐标是 ‎2.求标准方程要注意焦点位置和开口方向 问题2：顶点在原点、焦点在坐标轴上且经过点（3，2）的抛物线的条数有 ‎ 点拨：抛物线的类型一共有4种，经过第一象限的抛物线有2种，故满足条件的抛物线有2条 ‎3.研究几何性质，要具备数形结合思想，“两条腿走路”‎ 问题3：证明：以抛物线焦点弦为直径的圆与抛物线的准线相切 点拨：设为抛物线的焦点弦，F为抛物线的焦点，点分别是点在准线上的射影，弦的中点为M，则，点M到准线的距离为，以抛物线焦点弦为直径的圆总与抛物线的准线相切 ‎3、典型例题讲解：‎ 考点1 抛物线的定义 题型 利用定义,实现抛物线上的点到焦点的距离与到准线的距离之间的转换 ‎[例1 ]已知点P在抛物线y2 = 4x上，那么点P到点Q（2，－1）的距离与点P到抛物线焦点距离之和的最小值为 ‎ 解题思路：将点P到焦点的距离转化为点P到准线的距离 ‎[解析]过点P作准线的垂线交准线于点R，由抛物线的定义知，‎ ‎，当P点为抛物线与垂线的交点时，取得最小值，最小值为点Q到准线的距离 ,因准线方程为x=-1,故最小值为3‎ 总结：灵活利用抛物线的定义，就是实现抛物线上的点到焦点的距离与到准线的距离之间的转换，一般来说,用定义问题都与焦半径问题相关 练习：‎ ‎1.已知抛物线的焦点为，点，在抛物线上，且、、成等差数列， 则有 （　　）‎ A． B． ‎ C． D. ‎ ‎［解析］C 由抛物线定义，即：． ‎ ‎2. 已知点F是抛物线的焦点,M是抛物线上的动点,当最小时,‎ ‎ M点坐标是 ( )‎ A. B. C. D. ‎ ‎[解析] 设M到准线的距离为,则，当最小时，M点坐标是，选C 考点2 抛物线的标准方程 题型:求抛物线的标准方程 ‎[例2 ] 求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程：‎ ‎(1)过点(-3,2) (2)焦点在直线上 解题思路：以方程的观点看待问题，并注意开口方向的讨论.‎ ‎[解析] (1)设所求的抛物线的方程为或,‎ ‎ ∵过点(-3,2) ∴‎ ‎ ∴‎ ‎ ∴抛物线方程为或,‎ 前者的准线方程是后者的准线方程为 ‎ (2)令得，令得，‎ ‎ ∴抛物线的焦点为(4,0)或(0,-2),当焦点为(4,0)时,‎ ‎ ∴，此时抛物线方程;焦点为(0,-2)时 ‎ ∴，此时抛物线方程.‎ ‎ ∴所求抛物线方程为或,对应的准线方程分别是.‎ 总结：对开口方向要特别小心，考虑问题要全面 练习：‎ ‎3.若抛物线的焦点与双曲线的右焦点重合,则的值 ‎ ‎[解析]‎ ‎4. 对于顶点在原点的抛物线，给出下列条件：‎ ‎①焦点在y轴上；‎ ‎②焦点在x轴上；‎ ‎③抛物线上横坐标为1的点到焦点的距离等于6；‎ ‎④抛物线的通径的长为5；‎ ‎⑤由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）.‎ 能使这抛物线方程为y2=10x的条件是____________.（要求填写合适条件的序号）‎ ‎[解析] 用排除法，由抛物线方程y2=10x可排除①③④，从而②⑤满足条件.‎ ‎5.‎ ‎ 若抛物线的顶点在原点，开口向上，F为焦点，M为准线与Y轴的交点，A为抛物线上一点,且，求此抛物线的方程 ‎[解析] 设点是点在准线上的射影，则，由勾股定理知，点A的横坐标为，代入方程得或4，抛物线的方程或 考点3 抛物线的几何性质 题型：有关焦半径和焦点弦的计算与论证 ‎[例3 ]设A、B为抛物线上的点,且(O为原点),则直线AB必过的定点坐标为__________.‎ 解题思路：由特殊入手，先探求定点位置 ‎［解析］设直线OA方程为,由解出A点坐标为 解出B点坐标为，直线AB方程为,令得，直线AB必过的定点 总结：（1）由于是填空题，可取两特殊直线AB, 求交点即可；（2）B点坐标可由A点坐标用换k而得。‎ 练习：‎ ‎6. 若直线经过抛物线的焦点，则实数 ‎ ‎[解析]-1‎ ‎7.过抛物线焦点F的直线与抛物线交于两点A、B,若A、B在抛物线准线上的射影为,则 ( )‎ ‎ A. B. C. D. ‎ ‎[解析]C 基础巩固训练：‎ ‎1.过抛物线的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于，则这样的直线（ ）　　　　　　　　　　　　　　　　　　　　　‎ A.有且仅有一条 B.有且仅有两条 C.1条或2条 D.不存在 ‎[解析]C ，而通径的长为4．‎ ‎2.在平面直角坐标系中，若抛物线上的点到该抛物线焦点的距离为5，则点P的纵坐标为　（　　）‎ A. 3 B. 4 C. 5 D. 6‎ ‎[解析] B 利用抛物线的定义，点P到准线的距离为5，故点P的纵坐标为4．‎ ‎3.两个正数a、b的等差中项是，一个等比中项是，且则抛物线的焦点坐标为( ) ‎ A． B． C． D．‎ ‎[解析] D. ‎ ‎4. 如果，，…，是抛物线上的点，它们的横坐标依次为，，…，，F是抛物线的焦点，若成等差数列且，则=（ ）．‎ A．5 B．6 C． 7 D．9 ‎ ‎[解析]B 根据抛物线的定义，可知（，2，……，n），成等差数列且,,=6‎ ‎5、抛物线准线为l，l与x轴相交于点E，过F且倾斜角等于60°的直线与抛物线在x轴上方的部分相交于点A，AB⊥l，垂足为B，则四边形ABEF的面积等于（ ）‎ ‎ A． B． C． D．‎ ‎[解析] C. 过A作x轴的垂线交x轴于点H，设，则 ‎，‎ 四边形ABEF的面积=‎ ‎6、设是坐标原点，是抛物线的焦点，是抛物线上的一点，与轴正向的夹角为，则为 ．‎ ‎[解析]. ‎ 过A 作轴于D，令，则即，解得．‎ 综合提高训练 ‎7.在抛物线上求一点，使该点到直线的距离为最短，求该点的坐标 ‎[解析]解法1：设抛物线上的点，‎ 点到直线的距离，‎ 当且仅当时取等号，故所求的点为 解法2：当平行于直线且与抛物线相切的直线与抛物线的公共点为所求，设该直线方程为，代入抛物线方程得，‎ 由得，故所求的点为 ‎8. 已知抛物线（为非零常数）的焦点为，点为抛物线上一个动点，过点且与抛物线相切的直线记为．‎ ‎（1）求的坐标；‎ ‎（2）当点在何处时，点到直线的距离最小？‎ 解：（1）抛物线方程为 ‎ 故焦点的坐标为 ‎ ‎（2）设 ‎ ‎ ‎ 直线的方程是 ‎ ‎ ‎9. 设抛物线（）的焦点为 F，经过点 F的直线交抛物线于A、B两点．点 C在抛物线的准线上，且BC∥X轴．证明直线AC经过原点O．‎ 证明:因为抛物线（）的焦点为，所以经过点F的直线AB的方程可设为 ‎ ，代人抛物线方程得 ‎ ．‎ ‎ 若记，，则是该方程的两个根，所以 ‎．‎ 因为BC∥X轴，且点C在准线上，所以点C的坐标为，‎ 故直线CO的斜率为 即也是直线OA的斜率，所以直线AC经过原点O．‎ ‎10.椭圆上有一点M（-4，）在抛物线（p>0）的准线l上，抛物线的焦点也是椭圆焦点.‎ ‎（1）求椭圆方程；‎ ‎（2）若点N在抛物线上，过N作准线l的垂线，垂足为Q距离，求|MN|+|NQ|的最小值.‎ 解：（1）∵上的点M在抛物线（p>0）的准线l上，抛物线的焦点也是椭圆焦点.‎ ‎∴c=-4，p=8……①‎ ‎∵M（-4，）在椭圆上 ‎∴……②‎ ‎∵……③‎ ‎∴由①②③解得：a=5、b=3‎ ‎∴椭圆为 由p=8得抛物线为 设椭圆焦点为F（4，0），‎ 由椭圆定义得|NQ|=|NF|‎ ‎∴|MN|+|NQ|≥|MN|+|NF|=|MF|‎ ‎=，即为所求的最小值.‎ 参考例题：‎ ‎1、已知抛物线C的一个焦点为F（，0），对应于这个焦点的准线方程为x=-.‎ ‎（1）写出抛物线C的方程；‎ ‎（2）过F点的直线与曲线C交于A、B两点，O点为坐标原点，求△AOB重心G的轨迹方程；‎ ‎（3）点P是抛物线C上的动点，过点P作圆（x-3）2+y2=2的切线，切点分别是M，N.当P点在何处时，|MN|的值最小？求出|MN|的最小值.‎ 解：（1）抛物线方程为：y2=2x. （4分）‎ ‎（2）①当直线不垂直于x轴时，设方程为y=k(x-)，代入y2=2x，‎ 得：k2x2-(k2+2)x+.‎ 设A（x1，y1），B(x2，y2)，则x1+x2=，y1+y2=k(x1+x2-1)=.‎ 设△AOB的重心为G（x，y）则，‎ 消去k得y2=为所求， （6分）‎ ‎②当直线垂直于x轴时，A（，1），B（，-1）， （8分）‎ ‎△AOB的重心G（，0）也满足上述方程.‎ 综合①②得，所求的轨迹方程为y2=， （9分）‎ ‎（3）设已知圆的圆心为Q（3，0），半径r=，‎ 根据圆的性质有：|MN|=2. （11分）‎ 当|PQ|2最小时，|MN|取最小值，‎ 设P点坐标为(x0，y0)，则y=2x0.‎ ‎|PQ|2=（x0-3）2+ y= x-4x0+9=(x0-2)2+5，‎ ‎∴当x0=2，y0=±2时，|PQ|2取最小值5，‎ 故当P点坐标为（2，±2）时，|MN|取最小值. ‎ 抛物线专题练习 一、选择题（本大题共10小题，每小题5分，共50分）‎ ‎1．如果抛物线y 2=ax的准线是直线x=-1，那么它的焦点坐标为 （ A ）‎ A．（1, 0） B．（2, 0） C．（3, 0） D．（－1, 0）‎ ‎2．圆心在抛物线y 2=2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是 （ D ）‎ A．x2+ y 2-x-2 y -=0 B．x2+ y 2+x-2 y +1=0 ‎ C．x2+ y 2-x-2 y +1=0 D．x2+ y 2-x-2 y +=0‎ ‎3．抛物线上一点到直线的距离最短的点的坐标是 （ A ）‎ ‎ A．（1，1） B．（） C． D．（2，4）‎ ‎4．一抛物线形拱桥，当水面离桥顶2m时，水面宽4m，若水面下降1m，则水面宽为（ B ）‎ A．m B． 2m C．4.5m D．9m ‎5．平面内过点A（-2，0），且与直线x=2相切的动圆圆心的轨迹方程是 （ C ）‎ A． y 2=－2x B． y 2=－4x C．y 2=－8x D．y 2=－16x ‎6．抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的方程是 （ B ）‎ A． y 2=-2x B． y 2=-4x ‎ C． y 2=2x D． y 2=-4x或y 2=-36x ‎7．过抛物线y 2=4x的焦点作直线，交抛物线于A(x1, y 1) ，B(x2, y 2)两点，如果x1+ x2=6，那么|AB|= （ A ）‎ A．8 B．10 C．6 D．4‎ ‎8．把与抛物线y 2=4x关于原点对称的曲线按向量a平移，所得的曲线的方程是（C ）‎ ‎ A． B．‎ C． D． ‎ ‎9．过点M（2，4）作与抛物线y 2=8x只有一个公共点的直线l有 （ C ）‎ ‎ A．0条 B．1条 C．2条 D．3条 ‎10．过抛物线y =ax2(a>0)的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是p、q，则等于 （ C ）‎ A．2a B． C．4a D． ‎ 二、填空题（本大题共4小题，每小题6分，共24分）‎ ‎11．抛物线y 2=4x的弦AB垂直于x轴，若AB的长为4，则焦点到AB的距离为 2 ．‎ ‎12．抛物线y =2x2的一组斜率为k 的平行弦的中点的轨迹方程是 ．‎ ‎13．P是抛物线y 2=4x上一动点，以P为圆心，作与抛物线准线相切的圆，则这个圆一定经过一个定点Q，点Q的坐标是 （1，0） ．‎ ‎14．抛物线的焦点为椭圆的左焦点，顶点在椭圆中心，则抛物线方程为 ‎ 三、解答题（本大题共6小题，共76分）‎ ‎15．已知动圆M与直线y =2相切，且与定圆C：外切，求动圆圆心M的轨迹方程．(12分)‎ ‎[解析]：设动圆圆心为M（x，y），半径为r，则由题意可得M到C（0，-3）的距离与到直线y=3的距离相等，由抛物线的定义可知：动圆圆心的轨迹是以C（0，-3）为焦点，以y=3为准线的一条抛物线，其方程为．‎ ‎16．已知抛物线的顶点在原点，对称轴是x轴，抛物线上的点M（－3，m）到焦点的距离等于5，求抛物线的方程和m的值．（12分）‎ ‎[解析]：设抛物线方程为，则焦点F（），由题意可得 ‎ ，解之得或，‎ ‎ 故所求的抛物线方程为，‎ ‎17．动直线y =a，与抛物线相交于A点，动点B的坐标是，求线段AB中点M的轨迹的方程．(12分)‎ ‎[解析]：设M的坐标为（x，y），A（，），又B得 ‎ ‎ 消去，得轨迹方程为，即 ‎18．河上有抛物线型拱桥，当水面距拱桥顶5米时，水面宽为8米，一小船宽4米，高2米，载货后船露出水面上的部分高0.75米，问水面上涨到与抛物线拱顶相距多少米时，小船开始不能通航？(12分)‎ ‎[解析]：如图建立直角坐标系，‎ 设桥拱抛物线方程为，由题意可知，‎ B（4，-5）在抛物线上，所以，得，‎ ‎ 当船面两侧和抛物线接触时，船不能通航，设此时船面宽为AA’，则A（），由得，又知船面露出水面上部分高为0．75米，所以=2米 ‎19．如图，直线l1和l2相交于点M，l1⊥l2，点N∈l1．以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，|AM|=，|AN|=3，且|BN|=6．建立适当的坐标系，求曲线段C的方程．(14分)‎ ‎[解析]：如图建立坐标系，以l1为x轴，MN的垂直平分线为y轴，点O为坐标原点．由题意可知：曲线C是以点N为焦点，以l2为准线的抛物线的一段，其中A、B分别为C的端点．‎ 设曲线段C的方程为，‎ ‎ 其中分别为A、B的横坐标，．‎ ‎ 所以，． 由，得 ‎ ①‎ ‎ ②‎ 联立①②解得．将其代入①式并由p>0解得，或．‎ 因为△AMN为锐角三角形，所以，故舍去． ∴p=4，．‎ 由点B在曲线段C上，得．综上得曲线段C的方程为．‎ ‎ ‎ ‎20．已知抛物线．过动点M（，0）且斜率为1的直线与该抛物线交于不同的两点A、B，．‎ ‎（Ⅰ）求的取值范围；‎ ‎（Ⅱ）若线段AB的垂直平分线交轴于点N，求面积的最大值．(14分)‎ ‎ [解析]：（Ⅰ）直线的方程为，将，‎ 得 ． 设直线与抛物线两个不同交点的坐标为、，‎ 则 又，‎ ‎∴ ． ∵， ∴ ． 解得 ． ‎ ‎（Ⅱ）设AB的垂直平分线交AB于点Q，令坐标为，则由中点坐标公式，得 ‎， ． ‎ ‎∴ ． 又 为等腰直角三角形，‎ ‎∴ ， ∴ ‎ 即面积最大值为 ‎ ‎