通用版备战高考物理知识点最后冲刺大全八动量与能量 10页

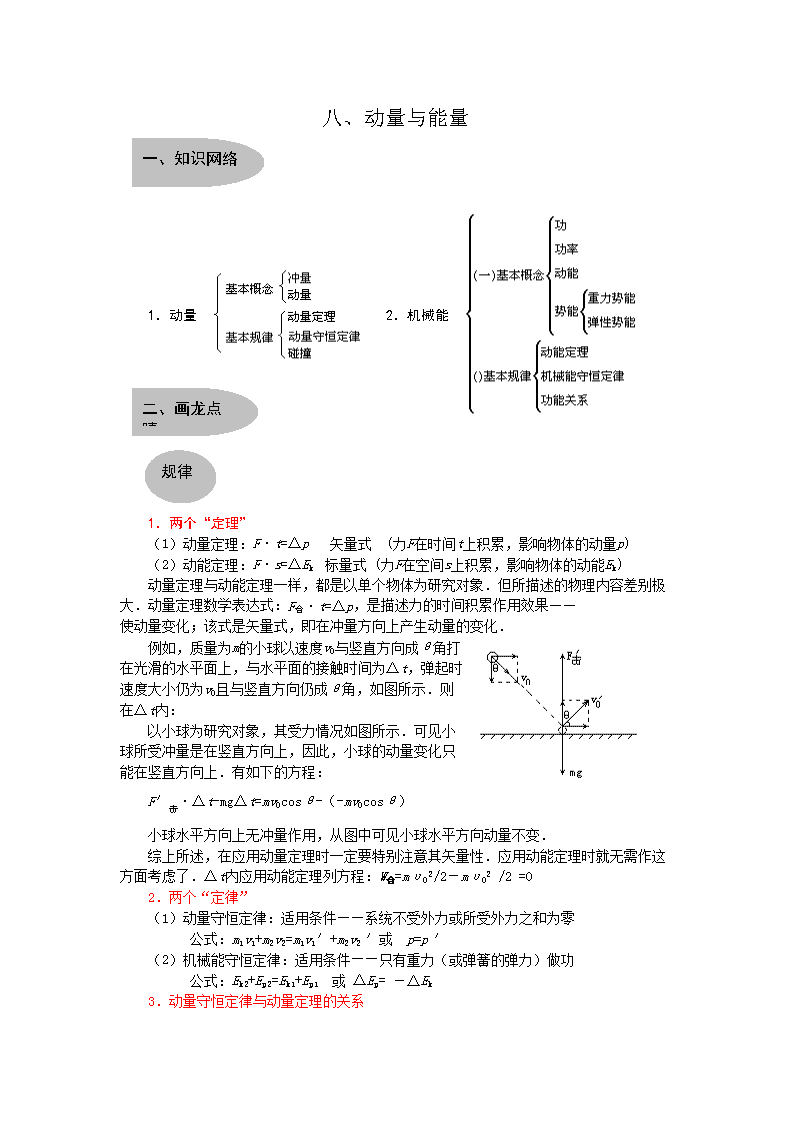
八、动量与能量 一、知识网络 ‎1．动量 2．机械能 二、画龙点睛 规律 ‎1．两个“定理”‎ ‎（1）动量定理：F·t=Δp 矢量式 (力F在时间t上积累，影响物体的动量p)‎ ‎（2）动能定理：F·s=ΔEk 标量式 (力F在空间s上积累，影响物体的动能Ek)‎ 动量定理与动能定理一样，都是以单个物体为研究对象．但所描述的物理内容差别极大．动量定理数学表达式：F合·t=Δp，是描述力的时间积累作用效果——使动量变化；该式是矢量式，即在冲量方向上产生动量的变化．‎ 例如，质量为m的小球以速度v0与竖直方向成θ角打在光滑的水平面上，与水平面的接触时间为Δt，弹起时速度大小仍为v0且与竖直方向仍成θ角，如图所示．则在Δt内：‎ 以小球为研究对象，其受力情况如图所示．可见小球所受冲量是在竖直方向上，因此，小球的动量变化只能在竖直方向上．有如下的方程：‎ F′击·Δt-mgΔt=mv0cosθ-（-mv0cosθ）‎ 小球水平方向上无冲量作用，从图中可见小球水平方向动量不变．‎ 综上所述，在应用动量定理时一定要特别注意其矢量性．应用动能定理时就无需作这方面考虑了．Δt内应用动能定理列方程：W合=mυ02/2－mυ02 /2 =0‎ ‎2．两个“定律”‎ ‎（1）动量守恒定律：适用条件——系统不受外力或所受外力之和为零 公式：m1v1+m2v2=m1v1′+m2v2 ′或 p=p ′‎ ‎（2）机械能守恒定律：适用条件——只有重力（或弹簧的弹力）做功 公式：Ek2+Ep2=Ek1+Ep1 或 ΔEp= －ΔEk ‎3．动量守恒定律与动量定理的关系 动量守恒定律的数学表达式为：m1v1+m2v2=m1v1′＋m2v2′，可由动量定理推导得出．‎ 如图所示，分别以m1和m2为研究对象，根据动量定理：‎ F1Δt= m1v1′- m1v1　 ①‎ F2Δt= m2v2′- m2v2　　 ②‎ F1=-F2　　　 ③‎ ‎∴ m1v1+m2v2=m1v1′＋m2v2′‎ 可见，动量守恒定律数学表达式是动量定理的综合解．动量定理可以解决动量守恒问题，只是较麻烦一些．因此，不能将这两个物理规律孤立起来．‎ ‎4．动能定理与能量守恒定律关系——理解“摩擦生热”(Q=f·Δs)‎ 设质量为m2的板在光滑水平面上以速度υ2运动，质量为m1的物块以速度υ1在板上同向运动，且υ1＞υ2，它们之间相互作用的滑动摩擦力大小为f，经过一段时间，物块的位移为s1，板的位移s2，此时两物体的速度变为υ′1和υ′2由动能定理得：‎ ‎ -fs1=m1υ1′2/2－m1υ12/2     ①‎ ‎ fs2=m2υ2′2/2－m2υ22/2         ②‎ 在这个过程中，通过滑动摩擦力做功，机械能不断转化为内能，即不断“生热”，由能量守恒定律及①②式可得：‎ Q=(m1υ12/2+m2υ22/2)－(m1υ1′2/2－m2υ2′2/2)=f(s1－s2)= f·Δs  ③‎ 由此可见，在两物体相互摩擦的过程中，损失的机械能（“生热”）等于摩擦力与相对位移的乘积。‎ 特别要指出，在用Q= f·Δs 计算摩擦生热时，正确理解是关键。这里分两种情况：‎ ‎（1）若一个物体相对于另一个物体作单向运动，Δs为相对位移；‎ ‎（2）若一个物体相对于另一个物体作往返运动，Δs为相对路程。‎ ‎5.相互作用中的动量与能量，三类碰撞中能量的变化： ‎(1)完全非弹性碰撞：动量守恒，机械能损失最大 ‎(2)完全弹性碰撞：动量守恒，机械能也守恒。 设两物体发生完全弹性碰撞，其中m1以v1匀速运动，m2静止。‎ 据 可得 讨论：(a)当m1＞m2时，v1′与v1方向一致；‎ ‎(b)当m1=m2时，v1′=0,v2′=v1，即m1与m2交换速度 ‎(c)当m1＜m2时，v1′反向，v2′与v1同向。‎ ‎(3)非完全弹性碰撞：为一般情况，只有动量守恒，机械能有损失，损失量不最大，亦不最小。‎ ‎6． 功和能的关系 做功的过程是物体能量的转化过程，做了多少功，就有多少能量发生了变化，功是能量转化的量度．‎ 动能定理 合外力对物体做的功等于物体动能的增量．即 重力做功与重力势能增量的关系 重力做正功，重力势能减少；重力做负功，重力势能增加．重力对物体所做的功等于物体重力势能增量的负值．即WG=EP1—EP2= —ΔEP 弹力做功与弹性势能增量的关系 弹力做正功，弹性势能减少；弹力做负功，弹性势能增加．弹力对物体所做的功等于物体弹性势能增量的负值．即W弹力=EP1—EP2= —ΔEP 功能原理 除重力和弹簧的弹力外，其他力对物体做的功等于物体机械能的增量．即 WF=E2—E1=ΔE 机械能守恒定律 在只有重力和弹簧的弹力做功的物体系内，动能和势能可以互相转化，但机械能的总量保持不变．即 EK2+EP2 = EK1+EP1， ‎ 或 ΔEK = —ΔEP 静摩擦力做功的 特点 ‎（1）静摩擦力可以做正功，也可以做负功，还可以不做功；‎ ‎（2）在静摩擦力做功的过程中，只有机械能的互相转移，而没有机械能与其他形式的能的转化，静摩擦力只起着传递机械能的作用；‎ ‎（3）相互摩擦的系统内，一对静摩擦力对系统所做功的和总是等于零．‎ 滑动摩擦力做功的特点 ‎（1）滑动摩擦力可以做正功，也可以做负功，还可以不做功；‎ ‎（2）相互摩擦的系统内，一对滑动摩擦力对系统所做功的和总表现为负功，其大小为 W= —fS相对 （S相对为相互摩擦的物体间的相对位移；若相对运动有往复性，则S相对为相对运动的路程．）‎ ‎（3）在滑动摩擦力对系统做功的过程中，系统的机械能转化为其他形式的能，其大小为 Q= fS相对 一对作用力与反作用力做功的特点 ‎(1)作用力做正功时，反作用力可以做正功，也可以做负功，还可以不做功；作用力做负功、不做功时，反作用力亦同样如此．‎ ‎(2)一对作用力与反作用力对系统所做功的总和可以是正功,也可以是负功,还可以零．‎ 例题： 质量为M的楔形物块上有圆弧轨道，静止在水平面上。质量为m的小球以速度v1向物块运动。不计一切摩擦，圆弧小于90°且足够长。求小球能上升到的最大高度H 和物块的最终速度v。解析：‎ 解析：系统水平方向动量守恒，全过程机械能也守恒。‎ 在小球上升过程中，由水平方向系统动量守恒得： 由系统机械能守恒得： 解得 全过程系统水平动量守恒，机械能守恒，得 ‎ 本题和上面分析的弹性碰撞基本相同，唯一的不同点仅在于重力势能代替了弹性势能。‎ 例题：动量分别为5kgžm/s和6kgžm/s的小球A、B沿光滑平面上的同一条直线同向运动，A追上B并发生碰撞后。若已知碰撞后A的动量减小了2kgžm/s，而方向不变，那么A、B质量之比的可能范围是什么？‎ 解析：A能追上B，说明碰前vA>vB,∴；碰后A的速度不大于B的速度， ；又因为碰撞过程系统动能不会增加， ，由以上不等式组解得： 此类碰撞问题要考虑三个因素：①碰撞中系统动量守恒；②碰撞过程中系统动能不增加；③碰前、碰后两个物体的位置关系（不穿越）和速度大小应保证其顺序合理。‎ 例题：设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块，并留在木块中不再射出，子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。‎ 解析：子弹和木块最后共同运动，相当于完全非弹性碰撞。‎ 从动量的角度看，子弹射入木块过程中系统动量守恒： ‎ ‎ 从能量的角度看，该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f，设子弹、木块的位移大小分别为s1、s2，如图所示，显然有s1-s2=d 对子弹用动能定理： ……①‎ 对木块用动能定理： ……②‎ ‎①、②相减得： ……③‎ 这个式子的物理意义是：fžd恰好等于系统动能的损失；根据能量守恒定律，系统动能的损失应该等于系统内能的增加；可见，即两物体由于相对运动而摩擦产生的热（机械能转化为内能），等于摩擦力大小与两物体相对滑动的路程的乘积（由于摩擦力是耗散力，摩擦生热跟路径有关，所以这里应该用路程，而不是用位移）。 ‎ 由上式不难求得平均阻力的大小： 至于木块前进的距离s2，可以由以上②、③相比得出： 从牛顿运动定律和运动学公式出发，也可以得出同样的结论。由于子弹和木块都在恒力作用下做匀变速运动，位移与平均速度成正比：‎ ‎ ‎ 一般情况下，所以s2<