2010年北京市高考数学试卷(理科) 23页

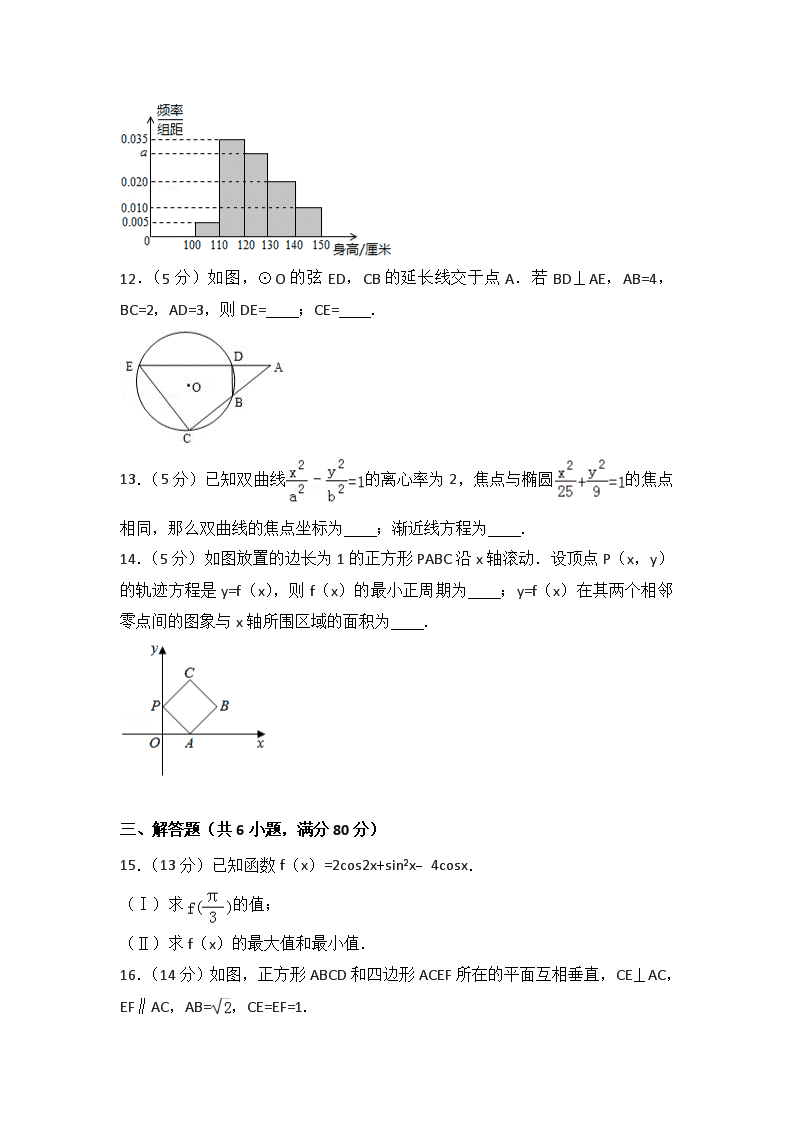
‎2010年北京市高考数学试卷（理科）‎ ‎　‎ 一、选择题（共8小题，每小题5分，满分40分）‎ ‎1．（5分）（北京卷理1）集合P={x∈Z|0≤x＜3}，M={x∈Z|x2＜9}，则P∩M=（　　）‎ A．{1，2} B．{0，1，2} C．{x|0≤x＜3} D．{x|0≤x≤3}‎ ‎2．（5分）在等比数列{an}中，a1=1，公比q≠1．若am=a1a2a3a4a5，则m=（　　）‎ A．9 B．10 C．11 D．12‎ ‎3．（5分）一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如图所，则该几何体的俯视图为（　　）‎ A． B． C． D．‎ ‎4．（5分）8名学生和2位老师站成一排合影，2位老师不相邻的排法种数为（　　）‎ A．A88A92 B．A88C92 C．A88A72 D．A88C72‎ ‎5．（5分）极坐标方程（ρ﹣1）（θ﹣π）=0（ρ≥0）表示的图形是（　　）‎ A．两个圆 B．两条直线 C．一个圆和一条射线 D．一条直线和一条射线 ‎6．（5分）若，是非零向量，“⊥”是“函数为一次函数”的（　　）‎ A．充分而不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎7．（5分）设不等式组表示的平面区域为D，若指数函数y=ax的图象上存在区域D上的点，则a的取值范围是（　　）‎ A．（1，3] B．[2，3] C．（1，2] D．[3，+∞]‎ ‎8．（5分）如图，正方体ABCD﹣A1B1C1D1的棱长为2，动点E、F在棱A1B1上，动点P，Q分别在棱AD，CD上，若EF=1，A1E=x，DQ=y，DP=z（x，y，z大于零），则四面体PEFQ的体积（　　）‎ A．与x，y，z都有关 B．与x有关，与y，z无关 C．与y有关，与x，z无关 D．与z有关，与x，y无关 ‎　‎ 二、填空题（共6小题，每小题5分，满分30分）‎ ‎9．（5分）在复平面内，复数对应的点的坐标为　　．‎ ‎10．（5分）在△ABC中，若b=1，c=，∠C=，则a=　　．‎ ‎11．（5分）从某小学随机抽取100名同学，将他们身高（单位：厘米）数据绘制成频率分布直方图（如图）．由图中数据可知a=　　．若要从身高在[120，130﹚，[130，140﹚，[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为　　．‎ ‎12．（5分）如图，⊙O的弦ED，CB的延长线交于点A．若BD⊥AE，AB=4，BC=2，AD=3，则DE=　　；CE=　　．‎ ‎13．（5分）已知双曲线的离心率为2，焦点与椭圆的焦点相同，那么双曲线的焦点坐标为　　；渐近线方程为　　．‎ ‎14．（5分）如图放置的边长为1的正方形PABC沿x轴滚动．设顶点P（x，y）的轨迹方程是y=f（x），则f（x）的最小正周期为　　；y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积为　　．‎ ‎　‎ 三、解答题（共6小题，满分80分）‎ ‎15．（13分）已知函数f（x）=2cos2x+sin2x﹣4cosx．‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求f（x）的最大值和最小值．‎ ‎16．（14分）如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，AB=，CE=EF=1．‎ ‎（Ⅰ）求证：AF∥平面BDE；‎ ‎（Ⅱ）求证：CF⊥平面BDE；‎ ‎（Ⅲ）求二面角A﹣BE﹣D的大小．‎ ‎17．（13分）某同学参加3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为，第二、第三门课程取得优秀成绩的概率分别为p，q（p＞q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ p a d ‎（Ⅰ）求该生至少有1门课程取得优秀成绩的概率；‎ ‎（Ⅱ）求数学期望Eξ．‎ ‎18．（13分）已知函数f（x）=ln（1+x）﹣x+x2（k≥0）．‎ ‎（Ⅰ）当k=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；‎ ‎（Ⅱ）求f（x）的单调区间．‎ ‎19．（14分）在平面直角坐标系xOy中，点B与点A（﹣1，1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于﹣．‎ ‎（Ⅰ）求动点P的轨迹方程；‎ ‎（Ⅱ）设直线AP和BP分别与直线x=3交于点M，N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由．‎ ‎20．（13分）已知集合Sn={X|X=（x1，x2，…，xn），xi∈{0，1}，i=1，2，…，n}（n≥2）对于A=（a1，a2，…an，），B=（b1，b2，…bn，）∈Sn，定义A与B的差为A﹣B=（|a1﹣b1|，|a2﹣b2|，…|an﹣bn|）；‎ A与B之间的距离为 ‎（Ⅰ）证明：∀A，B，C∈Sn，有A﹣B∈Sn，且d（A﹣C，B﹣C）=d（A，B）；‎ ‎（Ⅱ）证明：∀A，B，C∈Sn，d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数 ‎（Ⅲ）设P⊆Sn，P中有m（m≥2）个元素，记P中所有两元素间距离的平均值为．‎ 证明：≤．‎ ‎　‎ ‎2010年北京市高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共8小题，每小题5分，满分40分）‎ ‎1．（5分）（2010•北京）（北京卷理1）集合P={x∈Z|0≤x＜3}，M={x∈Z|x2＜9}，则P∩M=（　　）‎ A．{1，2} B．{0，1，2} C．{x|0≤x＜3} D．{x|0≤x≤3}‎ ‎【分析】由题意集合P={x∈Z|0≤x＜3}，M={x∈Z|x2＜9}，分别解出集合P，M，从而求出P∩M．‎ ‎【解答】解：∵集合P={x∈Z|0≤x＜3}，‎ ‎∴P={0，1，2}，‎ ‎∵M={x∈Z|x2＜9}，‎ ‎∴M={﹣2，﹣1，0，1，2}，‎ ‎∴P∩M={0，1，2}，‎ 故选B．‎ ‎　‎ ‎2．（5分）（2010•北京）在等比数列{an}中，a1=1，公比q≠1．若am=a1a2a3a4a5，则m=（　　）‎ A．9 B．10 C．11 D．12‎ ‎【分析】把a1和q代入am=a1a2a3a4a5，求得am=a1q10，根据等比数列通项公式可得m．‎ ‎【解答】解：am=a1a2a3a4a5=a1qq2q3q4=a1q10，因此有m=11‎ ‎　‎ ‎3．（5分）（2010•北京）一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如图所，则该几何体的俯视图为（　　）‎ A． B． C． D．‎ ‎【分析】从正视图和侧视图上分析，去掉的长方体的位置应该在的方位，然后判断俯视图的正确图形．‎ ‎【解答】解：由正视图可知去掉的长方体在正视线的方向，从侧视图可以看出去掉的长方体在原长方体的左侧，‎ 由以上各视图的描述可知其俯视图符合C选项．‎ 故选：C．‎ ‎　‎ ‎4．（5分）（2010•北京）8名学生和2位老师站成一排合影，2位老师不相邻的排法种数为（　　）‎ A．A88A92 B．A88C92 C．A88A72 D．A88C72‎ ‎【分析】本题要求两个教师不相邻，用插空法来解决问题，将所有学生先排列，有A88种排法，再将两位老师插入9个空中，共有A92种排法，根据分步计数原理得到结果．‎ ‎【解答】解：用插空法解决的排列组合问题，‎ 将所有学生先排列，有A88种排法，‎ 然后将两位老师插入9个空中，‎ 共有A92种排法，‎ ‎∴一共有A88A92种排法．‎ 故选A．‎ ‎　‎ ‎5．（5分）（2010•北京）极坐标方程（ρ﹣1）（θ﹣π）=0（ρ≥0）表示的图形是（　　）‎ A．两个圆 B．两条直线 C．一个圆和一条射线 D．一条直线和一条射线 ‎【分析】由题中条件：“（ρ﹣1）（θ﹣π）=0”得到两个因式分别等于零，结合极坐标的意义即可得到．‎ ‎【解答】解：方程（ρ﹣1）（θ﹣π）=0⇒ρ=1或θ=π，‎ ρ=1是半径为1的圆，‎ θ=π是一条射线．‎ 故选C．‎ ‎　‎ ‎6．（5分）（2010•北京）若，是非零向量，“⊥”是“函数为一次函数”的（　　）‎ A．充分而不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【分析】先判别必要性是否成立，根据一次函数的定义，得到，则成立，再判断充分性是否成立，由，不能推出函数为一次函数，因为时，函数是常数，而不是一次函数．‎ ‎【解答】解：，‎ 如，则有，‎ 如果同时有，则函数f（x）恒为0，不是一次函数，因此不充分，‎ 而如果f（x）为一次函数，则，因此可得，故该条件必要．‎ 故答案为B．‎ ‎　‎ ‎7．（5分）（2010•北京）设不等式组表示的平面区域为D，若指数函数y=ax的图象上存在区域D上的点，则a的取值范围是（　　）‎ A．（1，3] B．[2，3] C．（1，2] D．[3，+∞]‎ ‎【分析】先依据不等式组，结合二元一次不等式（组）与平面区域的关系画出其表示的平面区域，再利用指数函数y=ax的图象特征，结合区域的角上的点即可解决问题．‎ ‎【解答】解：作出区域D的图象，联系指数函数y=ax的图象，‎ 由得到点C（2，9），‎ 当图象经过区域的边界点C（2，9）时，a可以取到最大值3，‎ 而显然只要a大于1，图象必然经过区域内的点．‎ 故选：A．‎ ‎　‎ ‎8．（5分）（2010•北京）如图，正方体ABCD﹣A1B1C1D1的棱长为2，动点E、F在棱A1B1上，动点P，Q分别在棱AD，CD上，若EF=1，A1E=x，DQ=y，DP=z（x，y，z大于零），则四面体PEFQ的体积（　　）‎ A．与x，y，z都有关 B．与x有关，与y，z无关 C．与y有关，与x，z无关 D．与z有关，与x，y无关 ‎【分析】四面体PEFQ的体积，找出三角形△EFQ面积是不变量，P到平面的距离是变化的，从而确定选项．‎ ‎【解答】解：从图中可以分析出，△EFQ的面积永远不变，为面A1B1CD面积的，‎ 而当P点变化时，它到面A1B1CD的距离是变化的，因此会导致四面体体积的变化．‎ 故选D．‎ ‎　‎ 二、填空题（共6小题，每小题5分，满分30分）‎ ‎9．（5分）（2010•北京）在复平面内，复数对应的点的坐标为　（﹣1，1）　．‎ ‎【分析】首先进行复数的除法运算，分子和分母同乘以分母的共轭复数，分子和分母进行复数的乘法运算，得到最简形式即复数的代数形式，写出复数对应的点的坐标．‎ ‎【解答】解：∵，‎ ‎∴复数在复平面上对应的点的坐标是（﹣1，1）‎ 故答案为：（﹣1，1）‎ ‎　‎ ‎10．（5分）（2010•北京）在△ABC中，若b=1，c=，∠C=，则a=　1　．‎ ‎【分析】先根据b，c，∠c，由正弦定理可得sinB，进而求得B，再根据正弦定理求得a．‎ ‎【解答】解：在△ABC中由正弦定理得，‎ ‎∴sinB=，‎ ‎∵b＜c，‎ 故B=，则A=‎ 由正弦定理得 ‎∴a==1‎ 故答案为：1‎ ‎　‎ ‎11．（5分）（2010•北京）从某小学随机抽取100名同学，将他们身高（单位：厘米）数据绘制成频率分布直方图（如图）．由图中数据可知a=　0.03　．若要从身高在[120，130﹚，[130，140﹚，[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为　3　．‎ ‎【分析】欲求a，可根据直方图中各个矩形的面积之和为1，列得一元一次方程，解出a，欲求选取的人数，可先由直方图找出三个区域内的学生总数，及其中身高在[140，150]内的学生人数，再根据分层抽样的特点，代入其公式求解．‎ ‎【解答】解：∵直方图中各个矩形的面积之和为1，‎ ‎∴10×（0.005+0.035+a+0.02+0.01）=1，‎ 解得a=0.03．‎ 由直方图可知三个区域内的学生总数为100×10×（0.03+0.02+0.01）=60人．‎ 其中身高在[140，150]内的学生人数为10人，‎ 所以身高在[140，150]范围内抽取的学生人数为×10=3人．‎ 故答案为：0.03，3．‎ ‎　‎ ‎12．（5分）（2010•北京）如图，⊙O的弦ED，CB的延长线交于点A．若BD⊥AE，AB=4，BC=2，AD=3，则DE=　5　；CE=　　．‎ ‎【分析】首先根据题中圆的切线条件再依据割线定理求得一个线段AE的长，再根据勾股定理的线段的关系可求得CE的长度即可．‎ ‎【解答】解：首先由割线定理不难知道AB•AC=AD•AE，‎ 于是AE=8，DE=5，又BD⊥AE，‎ 故BE为直径，因此∠C=90°，‎ 由勾股定理可知CE2=AE2﹣AC2=28，‎ 故CE=．‎ 故填：5；．‎ ‎　‎ ‎13．（5分）（2010•北京）已知双曲线的离心率为2，焦点与椭圆的焦点相同，那么双曲线的焦点坐标为　（4，0），（﹣4，0）　；渐近线方程为　y=x　．‎ ‎【分析】先根据椭圆的方程求出焦点坐标，得到双曲线的c值，再由离心率求出a的值，最后根据b=得到b的值，可得到渐近线的方程．‎ ‎【解答】解：∵椭圆的焦点为（4，0）（﹣4，0），故双曲线中的c=4，且满足=2，故a=2，‎ b=，所以双曲线的渐近线方程为y=±=±x 故答案为：（4，0），（﹣4，0）；y=x ‎　‎ ‎14．（5分）（2010•北京）如图放置的边长为1的正方形PABC沿x轴滚动．设顶点P（x，y）的轨迹方程是y=f（x），则f（x）的最小正周期为　4　；y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积为　π+1　．‎ ‎【分析】正方形PABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续．类似地，正方形PABC可以沿x轴负方向滚动．‎ ‎【解答】解：从某一个顶点（比如A）落在x轴上的时候开始计算，到下一次A点落在x轴上，‎ 这个过程中四个顶点依次落在了x轴上，而每两个顶点间距离为正方形的边长1，因此该函数的周期为4．‎ 下面考察P点的运动轨迹，不妨考察正方形向右滚动，‎ P点从x轴上开始运动的时候，首先是围绕A点运动个圆，该圆半径为1，‎ 然后以B点为中心，滚动到C点落地，其间是以BP为半径，旋转90°，‎ 然后以C为圆心，再旋转90°，这时候以CP为半径，‎ 因此最终构成图象如下：‎ 故其与x轴所围成的图形面积为 ‎．‎ 故答案为：4，π+1‎ ‎　‎ 三、解答题（共6小题，满分80分）‎ ‎15．（13分）（2010•北京）已知函数f（x）=2cos2x+sin2x﹣4cosx．‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求f（x）的最大值和最小值．‎ ‎【分析】（Ⅰ）把x=代入到f（x）中，利用特殊角的三角函数值求出即可；‎ ‎（Ⅱ）利用同角三角函数间的基本关系把sin2x变为1﹣cos2x，然后利用二倍角的余弦函数公式把cos2x变为2cos2x﹣1，得到f（x）是关于cosx的二次函数，利用配方法把f（x）变成二次函数的顶点式，根据cosx的值域，利用二次函数求最值的方法求出f（x）的最大值和最小值即可．‎ ‎【解答】解：（Ⅰ）=；‎ ‎（Ⅱ）f（x）=2（2cos2x﹣1）+（1﹣cos2x）﹣4cosx ‎=3cos2x﹣4cosx﹣1‎ ‎=，‎ 因为cosx∈[﹣1，1]，‎ 所以当cosx=﹣1时，f（x）取最大值6；当时，取最小值﹣．‎ ‎　‎ ‎16．（14分）（2010•北京）如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，AB=，CE=EF=1．‎ ‎（Ⅰ）求证：AF∥平面BDE；‎ ‎（Ⅱ）求证：CF⊥平面BDE；‎ ‎（Ⅲ）求二面角A﹣BE﹣D的大小．‎ ‎【分析】（Ⅰ）设AC与BD交于点G，则在平面BDE中，可以先证明四边形AGEF为平行四边形⇒EG∥AF，就可证：AF∥平面BDE；‎ ‎（Ⅱ）先以C为原点，建立空间直角坐标系C﹣xyz．把对应各点坐标求出来，可以推出•=0和•=0，就可以得到CF⊥平面BDE ‎（Ⅲ）先利用（Ⅱ）找到=（，，1），是平面BDE的一个法向量，再利用平面ABE的法向量•=0和•=0，求出平面ABE的法向量，就可以求出二面角A﹣BE﹣D的大小．‎ ‎【解答】解：证明：（I）设AC与BD交于点G，‎ 因为EF∥AG，且EF=1，AG=AC=1，‎ 所以四边形AGEF为平行四边形．所以AF∥EG．‎ 因为EG⊂平面BDE，AF⊄平面BDE，‎ 所以AF∥平面BDE．‎ ‎（II）因为正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，‎ 所以CE⊥平面ABCD．‎ 如图，以C为原点，建立空间直角坐标系C﹣xyz．‎ 则C（0，0，0），A（，，0），D（，0，0），E（0，0，1），F（，，1）．‎ 所以=（，，1），=（0，﹣，1），=（﹣，0，1）．‎ 所以•=0﹣1+1=0，•=﹣1+0+1=0．‎ 所以CF⊥BE，CF⊥DE，所以CF⊥平面BDE ‎（III）由（II）知，=（，，1），是平面BDE的一个法向量，‎ 设平面ABE的法向量=（x，y，z），则•=0，•=0．‎ 即 所以x=0，且z=y．令y=1，则z=．所以n=（），从而cos（，）=‎ 因为二面角A﹣BE﹣D为锐角，所以二面角A﹣BE﹣D为．‎ ‎　‎ ‎17．（13分）（2010•北京）某同学参加3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为，第二、第三门课程取得优秀成绩的概率分别为p，q（p＞q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ p a d ‎（Ⅰ）求该生至少有1门课程取得优秀成绩的概率；‎ ‎（Ⅱ）求数学期望Eξ．‎ ‎【分析】（I）由题意知事件该生至少有一门课程取得优异成绩与事件“ξ=0”是对立的，要求该生至少有一门课程取得优秀成绩的概率，需要先知道该生没有一门课程优秀，根据对立事件的概率求出结果．‎ ‎（II）由题意可知，需要先求出分布列中的概率a和b的值，根据互斥事件的概率和相互独立事件同时发生的概率，得到这两个值，求出概率之后，问题就变为求期望．‎ ‎【解答】解：事件A表示“该生第i门课程取得优异成绩”，i=1，2，3．‎ 由题意可知 ‎（I）由于事件“该生至少有一门课程取得优异成绩”与事件“ξ=0”是对立的，‎ ‎∴该生至少有一门课程取得优秀成绩的概率是 ‎1﹣P（ξ=0）=1﹣‎ ‎（II）由题意可知，‎ P（ξ=0）=，‎ P（ξ=3）=‎ 整理得p=．‎ ‎∵a=P（ξ=1）=‎ ‎=‎ ‎=‎ d=P（ξ=2）=1﹣P（ξ=0）﹣P（ξ=1）﹣P（ξ=3）=‎ ‎∴Eξ=0×P（ξ=0）+1×P（ξ=1）+2×P（ξ=2）+3×P（ξ=3）=‎ ‎　‎ ‎18．（13分）（2010•北京）已知函数f（x）=ln（1+x）﹣x+x2（k≥0）．‎ ‎（Ⅰ）当k=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；‎ ‎（Ⅱ）求f（x）的单调区间．‎ ‎【分析】（I）根据导数的几何意义求出函数f（x）在x=1处的导数，从而求出切线的斜率，然后求出切点坐标，再用点斜式写出直线方程，最后化简成一般式即可；‎ ‎（II）先求出导函数f'（x），讨论k=0，0＜k＜1，k=1，k＞1四种情形，在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0即可．‎ ‎【解答】解：（I）当K=2时，‎ 由于所以曲线y=f（x）在点（1，f（1））处的切线方程为 ‎．即3x﹣2y+2ln2﹣3=0‎ ‎（II）f'（x）=﹣1+kx（x＞﹣1）‎ 当k=0时，‎ 因此在区间（﹣1，0）上，f'（x）＞0；在区间（0，+∞）上，f'（x）＜0；‎ 所以f（x）的单调递增区间为（﹣1，0），单调递减区间为（0，+∞）；‎ 当0＜k＜1时，，得；‎ 因此，在区间（﹣1，0）和上，f'（x）＞0；在区间上，f'（x）＜0；‎ 即函数f（x）的单调递增区间为（﹣1，0）和，单调递减区间为（0，）；‎ 当k=1时，．f（x）的递增区间为（﹣1，+∞）‎ 当k＞1时，由，得；‎ 因此，在区间和（0，+∞）上，f'（x）＞0，在区间上，f'（x）＜0；‎ 即函数f（x）的单调递增区间为和（0，+∞），单调递减区间为．‎ ‎　‎ ‎19．（14分）（2010•北京）在平面直角坐标系xOy中，点B与点A（﹣1，1）关于原点O对称，P是动点，且直线AP与BP的斜率之积等于﹣．‎ ‎（Ⅰ）求动点P的轨迹方程；‎ ‎（Ⅱ）设直线AP和BP分别与直线x=3交于点M，N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由．‎ ‎【分析】（Ⅰ）设点P的坐标为（x，y），先分别求出直线AP与BP的斜率，再利用直线AP与BP的斜率之间的关系即可得到关系式，化简后即为动点P的轨迹方程；‎ ‎（Ⅱ）对于存在性问题可先假设存在，由面积公式得：．根据角相等消去三角函数得比例式，最后得到关于点P的纵坐标的方程，解之即得．‎ ‎【解答】解：（Ⅰ）因为点B与A（﹣1，1）关于原点O对称，所以点B得坐标为（1，﹣1）．‎ 设点P的坐标为（x，y）‎ 化简得x2+3y2=4（x≠±1）．‎ 故动点P轨迹方程为x2+3y2=4（x≠±1）‎ ‎（Ⅱ）解：若存在点P使得△PAB与△PMN的面积相等，设点P的坐标为（x0，y0）‎ 则．‎ 因为sin∠APB=sin∠MPN，‎ 所以 所以=‎ 即（3﹣x0）2=|x02﹣1|，解得 因为x02+3y02=4，所以 故存在点P使得△PAB与△PMN的面积相等，此时点P的坐标为（）．‎ ‎　‎ ‎20．（13分）（2010•北京）已知集合Sn={X|X=（x1，x2，…，xn），xi∈{0，1}，i=1，2，…，n}（n≥2）对于A=（a1，a2，…an，），B=（b1，b2，…bn，）∈Sn ‎，定义A与B的差为A﹣B=（|a1﹣b1|，|a2﹣b2|，…|an﹣bn|）；‎ A与B之间的距离为 ‎（Ⅰ）证明：∀A，B，C∈Sn，有A﹣B∈Sn，且d（A﹣C，B﹣C）=d（A，B）；‎ ‎（Ⅱ）证明：∀A，B，C∈Sn，d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数 ‎（Ⅲ）设P⊆Sn，P中有m（m≥2）个元素，记P中所有两元素间距离的平均值为．‎ 证明：≤．‎ ‎【分析】（Ⅰ）因为每个数位上都是0或者1，取差的绝对值仍然是0或者1，符合Sn的要求．‎ 然后是减去C的数位，不管减去的是0还是1，每一个a和每一个b都是同时减去的，‎ 因此不影响他们原先的差．‎ ‎（Ⅱ）先比较A和B有几个不同（因为距离就是不同的有几个），然后比较A和C有几个不同，‎ 这两者重复的（就是某一位上A和B不同，A和C不同，那么这一位上B和C就相同）去掉两次 ‎（因为在前两次比较中各计算了一次），剩下的就是B和C的不同数目，‎ 很容易得到这样的关系式：h=k+l﹣2i，从而三者不可能同为奇数．‎ ‎（Ⅲ）首先理解P中会出现Cm2个距离，所以平均距离就是距离总和再除以Cm2，‎ 而距离的总和仍然可以分解到每个数位上，第一位一共产生了多少个不同，‎ 第二位一共产生了多少个不同，如此下去，直到第n位．然后思考，‎ 第一位一共m个数，只有0和1会产生一个单位距离，因此只要分开0和1的数目即可，‎ 等算出来，一切就水到渠成了．‎ 此外，这个问题需要注意一下数学语言的书写规范．‎ ‎【解答】解：（1）设A=（a1，a2，…，an），B=（b1，b2，…，bn），C=（c1‎ ‎，c2，…，cn）∈Sn 因ai，bi∈0，1，故|ai﹣bi|∈0，1，（i=1，2，…，n）a1b1∈0，1，‎ 即A﹣B=（|a1﹣b1|，|a2﹣b2|，…，|an﹣bn|）∈Sn 又ai，bi，ci∈（0，1），i=1，2，…，n 当ci=0时，有||ai﹣ci|﹣|bi﹣ci||=|ai﹣bi|；‎ 当ci=1时，有||ai﹣ci|﹣|bi﹣ci||=|（1﹣ai）﹣（1﹣bi）=|ai﹣bi|‎ 故 ‎（2）设A=（a1，a2，…，an），B=（b1，b2，…，bn），C=（c1，c2，…，cn）∈Sn 记d（A，B）=k，d（A，C）=l，d（B，C）=h 记O=（0，0，…，0）∈Sn，由第一问可知：‎ d（A，B）=d（A﹣A，B﹣A），d=（O，B﹣A）=k d（A，C）=d（A﹣A，C﹣A）=d（O，C﹣A）=l d（B，C）=d（B﹣A，C﹣A）=h 即|bi﹣ai|中1的个数为k，|ci﹣ai|中1的个数为l，（i=1，2，…，n）‎ 设t是使|bi﹣ai|=|ci﹣ai|=1成立的i的个数，则有h=k+l﹣2t，‎ 由此可知，k，l，h不可能全为奇数，即d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数．‎ ‎（3）显然P中会产生Cm2个距离，也就是说，其中表示P中每两个元素距离的总和．‎ 分别考察第i个位置，不妨设P中第i个位置一共出现了ti个1，那么自然有m﹣ti个0，因此在这个位置上所产生的距离总和为，（i=1，2，…，n），‎ 那么n个位置的总和 即 ‎　‎ 参与本试卷答题和审题的老师有：zhiyuan；zhwsd；qiss；涨停；yhx01248；xuanlv；wsj1012；geyanli；sllwyn；庞会丽；minqi5；Linaliu（排名不分先后）‎ 菁优网 ‎2017年2月3日