上海市高考数学压轴卷试题目理含解析 18页

‎2014年上海高考数学押题卷（理）‎ 考生注意：‎ ‎1.答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号，并将核对后的条形码贴在指定位置上，在答题纸反面清楚地填写姓名.‎ ‎2.本试卷共有23道试题，满分150分.考试时间120分钟.‎ 填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.‎ 函数的定义域为_____________‎ 已知是抛物线的焦点，在抛物线上，M（3,2）为线段AB的中点，则的面积为_____________‎ 已知是定义在上的奇函数.当时，，则不等式 的解集是_____________‎ 已知数列其前项和为，且，则数列的通项公式为_____________‎ 零向量满足,则夹角的取值范围是_____________‎ 在的展开式中含有 ，则=_____________‎ 已知复数，则b的取值范围是_____________‎ 已知_____________‎ 红、黄、蓝三色灯泡分别有3、2、2支，把它们挂成一排，要求红色灯泡不能全部相邻，则看到的不同效果有_____________个。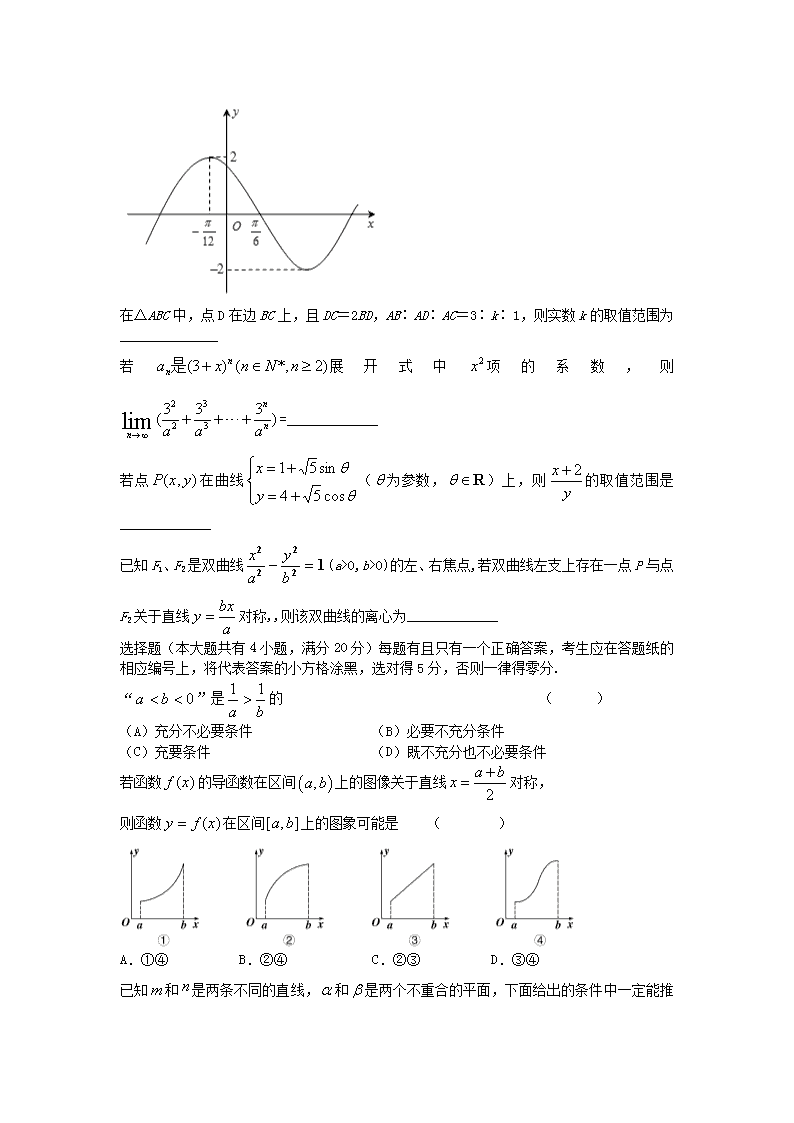‎ 已知函数（其中，，)的部分图象如图所示。如果对函数g(x)的图像进行如下变化:横坐标扩大为原来的2倍，纵坐标不变，也可得到f(x)函数的图像，则函数g(x)的解析式是_____________‎ 在△ABC中，点D在边BC上，且DC＝2BD，AB∶AD∶AC＝3∶k∶1，则实数k的取值范围为______________‎ 若展开式中项的系数，则=_____________‎ 若点在曲线（为参数，）上，则的取值范围是_____________‎ 已知F1、F2是双曲线(a>0,b>0)的左、右焦点,若双曲线左支上存在一点P与点F2关于直线对称,,则该双曲线的离心为_____________‎ 选择题（本大题共有4小题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分.‎ ‎“”是的 （ ）‎ ‎（A）充分不必要条件 （B）必要不充分条件 ‎（C）充要条件 （D）既不充分也不必要条件 若函数的导函数在区间上的图像关于直线对称，‎ 则函数在区间上的图象可能是 （ ）‎ A．①④ B．②④ C．②③ D．③④‎ 已知和是两条不同的直线，和是两个不重合的平面，下面给出的条件中一定能推出的是 （ ）‎ ‎（A）且 （B）且 ‎ ‎（C）且 （D）且 若数列{an}满足－＝d(n∈N*，d为常数)，则称数列{an}为“调和数列”．已知正项数列{}为“调和数列”，且b1＋b2＋…＋b9＝90，则b4·b6的最大值是 （ ）‎ A．10 B．100 C．200 D．400‎ 解答题（本大题共有5下题，满分74分）解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.‎ ‎（本题满分12分）‎ 如图，平面ABB1A1为圆柱OO1的轴截面，点C为上的点， 点M为BC中点．‎ ‎（I）求证：B1M∥平面O1AC；‎ ‎（II）若AB＝AA1，∠CAB=30°，求二面角C-AO1 -B的余弦值．‎ ‎（本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分.‎ 已知函数 ‎（1）求函数的单调区间；‎ ‎（2）若函数在上有且只有一个零点，求实数的取值范围；‎ ‎（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.‎ A B D O C x y ‎(第16题图)‎ 在平面直角坐标系xOy中，角α的顶点是坐标原点，始边为x轴的正半轴，终边与单位圆O交于点A(x1 ，y1 )，α∈(，)．将角α终边绕原点按逆时针方向旋转，交单位圆于点B(x2，y2)．‎ ‎（1）若x1＝，求x2；‎ ‎△BOD的面积分别为S1，S2，且S1＝S2，求tanα的值．‎ ‎ (本题满分16分)本题共有2个小题，第1小题满分6分，第2小题满分10分.‎ 在数列中，a1=2，b1=4，且成等差数列， 成等比数列（）‎ ‎（Ⅰ）求a2，a3，a4及b2，b3，b4，由此归纳出的通项公式，并证明你的结论；‎ ‎（Ⅱ）证明：‎ ‎（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分.‎ 在平面直角坐标系xOy中．已知，平面上一动点P满足|PM|+|PN|=4记动点P的轨迹为D．‎ ‎（I）求轨迹D的方程，‎ ‎（Ⅱ）设过点E（0．1）且不垂直于坐标轴的直线与轨迹D相交于A，B两点，若在y轴上存在一点Q，使得直QA，QB关于y轴对称．求出点Q的坐标；‎ ‎（Ⅲ）是否存在不过点E（0，1）且不垂直于坐标轴的直线，它与轨迹D及圆 从左到右依次交于C，D，F，G四点，且满足？若存在，求出当△OCG的面积S取得最小值时k2的值；若小存在，请说明理由．‎ ‎2014年上海高考数学押题卷（理）‎ 填空题 ‎（2,3） 2. 3. ‎ ‎ 5. 6. 1‎ ‎ 8. 9. 180‎ ‎ 11. (，) 12. 18‎ ‎13． 14．‎ 选择题 ‎15. A 16. D 17. C 18. B 解答题 ‎ （1）证明省略. （2） ．‎ ‎（1）‎ ‎ （2） ．‎ ‎（1）x2 = －； （2）tanα＝2．‎ ‎（1） ;证明省略. ‎ ‎ （2）证明省略.‎ ‎（1） （Ⅱ） Q(0,4). （Ⅲ）存在满足题意的直线；.‎ ‎============================= 详细解析见下 填空题 ‎【答案】 （2,3）‎ ‎ 【解析】 ‎ ‎【答案】 ‎ ‎ 【解析】‎ ‎ ‎ ‎【答案】 ‎ ‎ 【解析】‎ ‎ ‎ ‎【答案】 ‎ ‎ 【解析】 ‎ ‎【答案】 ‎ ‎ 【解析】 ‎ ‎。‎ ‎【答案】 1‎ ‎ 【解析】‎ 在的展开式中含有 ‎ ‎【答案】 ‎ ‎ 【解析】‎ ‎【答案】 ‎ ‎ 【解析】 ‎ ‎ ‎ ‎【答案】 180‎ ‎ 【解析】 ‎ ‎ 先无限制全排列，再剔除不符合条件的排列，最后再进行组合。 ‎ ‎【答案】 ‎ ‎【解析】‎ ‎【答案】 (，) ‎ ‎【解析】‎ ‎ ‎ ‎【答案】 18‎ ‎【解析】‎ 若展开式中项的系数，则 ‎ ‎ ‎【答案】 ‎ ‎【解析】 ‎ ‎ ‎ ‎【答案】 ‎ ‎【解析】由题知，为渐近线方程，‎ ‎ ‎ ‎【答案】 A ‎【解析】‎ ‎ ‎ ‎【答案】 D ‎【解析】‎ ‎ 由题知，，‎ 则函数的图象在区间上中心对称，图像③④符合，故选D 。‎ ‎【答案】 C ‎【解析】‎ ‎【答案】 B ‎ 【解析】‎ 正项数列{}为“调和数列”，若数列{bn}为等差数列，90=b1＋b2＋…＋b9＝，所以b4·b6的最大值为100，选B.‎ ‎【答案】（1）证明省略. （2） ．‎ ‎ 【解析】‎ ‎【答案】（1）‎ ‎（2） ．‎ ‎ 【解析】‎ A B D O C x y ‎(21题图)‎ ‎【答案】（1）x2 = －； （2）tanα＝2．‎ ‎【解析】‎ ‎（1）解法一：因为x1＝，y1＞0，所以y1＝＝．‎ ‎ 所以sinα＝，cosα＝． ………………………3分 所以x2＝cos(α＋)＝cosαcos－sinαsin＝－． …………………………………6分 ‎ 解法二：因为x1＝，y1＞0，所以y1＝＝．A(，)，则＝(，)，…………2分 ‎ ＝(x2，y2)， 因为·＝||||cos∠AOB，所以x2＋y2＝ ……4分 ‎ 又x22＋y22＝1，联立消去y2得50 x22－30x2－7＝0‎ ‎ 解得x2＝－或，又x2＜0，所以x2＝－． ………………………6分 ‎ 解法三：因为x1＝，y1＞0，所以y1＝＝． 因此A(，)，所以tanα＝．………2分 ‎ 所以tan(α＋)＝＝－7，所以直线OB的方程为y＝－7x ……………4分 ‎ 由得x＝±，又x2＜0，所以x2＝－． …………………6分 ‎（2）S1＝sinαcosα＝－sin2α． …………………………………………8分 因为α(，)，所以α＋(，)．‎ ‎ 所以S2＝－sin(α＋)cos(α＋)＝－sin(2α＋)＝－cos2α．……………………………10分 ‎ 因为S1＝S2，所以sin2α＝－cos2α，即tan2α＝－． …………………………………12分 所以＝－，解得tanα＝2或tanα＝－． 因为α(，)，所以tanα＝2．………14分 ‎ 【KS5U答案】‎ ‎（1） ;证明省略. ‎ ‎（2）证明省略.‎ ‎ 【KS5U解析】‎ ‎（Ⅰ）由条件得 由此可得 ‎．‎ 猜测． 4分 用数学归纳法证明：‎ ‎①当n=1时，由上可得结论成立．‎ ‎②假设当n=k时，结论成立，即 ‎，‎ 那么当n=k+1时，‎ ‎．‎ 所以当n=k+1时，结论也成立．‎ 由①②，可知对一切正整数都成立． 7分 ‎（Ⅱ）n≥1时，．n≥2时，由（Ⅰ）知． ‎ 故 15分 综上，原不等式成立． 16分 ‎【KS5U答案】‎ ‎（I）（1）‎ ‎（Ⅱ） Q(0,4).‎ ‎（Ⅲ）存在满足题意的直线；.‎ ‎ 【KS5U解析】‎