高考选修热学计算题训练 4页

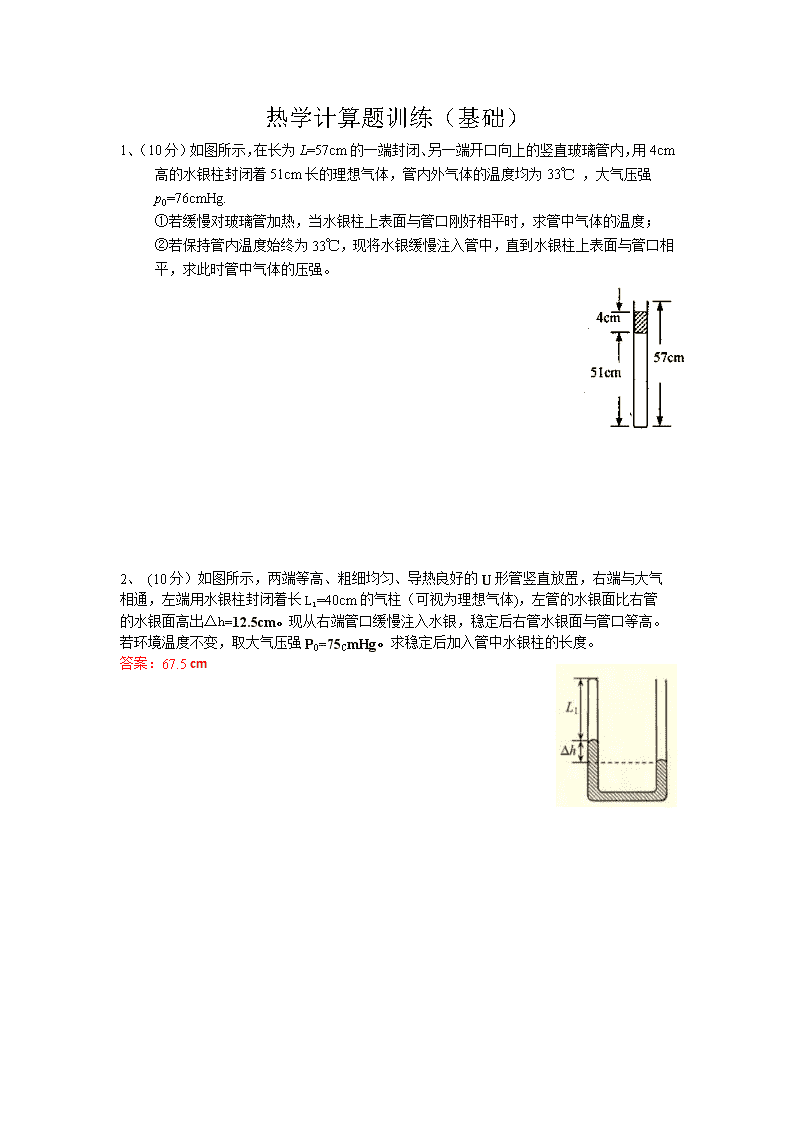
热学计算题训练（基础）‎ ‎1、（10分）如图所示，在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内，用4cm高的水银柱封闭着51cm长的理想气体，管内外气体的温度均为33℃ ，大气压强p0=76cmHg.‎ ‎①若缓慢对玻璃管加热，当水银柱上表面与管口刚好相平时，求管中气体的温度；‎ ‎②若保持管内温度始终为33℃，现将水银缓慢注入管中，直到水银柱上表面与管口相平，求此时管中气体的压强。‎ ‎2、 (10分）如图所示，两端等高、粗细均匀、导热良好的U形管竖直放置，右端与大气相通，左端用水银柱封闭着长L1=40cm的气柱（可视为理想气体)，左管的水银面比右管的水银面高出Δh=12.5cm。现从右端管口缓慢注入水银，稳定后右管水银面与管口等高。若环境温度不变，取大气压强P0=75CmHg。求稳定后加入管中水银柱的长度。‎ 答案：67.5 cm ‎3、(9分）如图所示，粗细均匀内壁光滑的细玻璃管长L=90cm，用长为h=15cm的水银柱封闭一段气柱（可视为理想气体)，开始时玻璃管水平放置，气柱长l=30cm，取大气压强P0=75cmHg。将玻璃管由水平位置缓慢转至竖直放置（管口向上)，‎ 求：①玻璃管转至竖直放置后气柱的长度；答案：25 cm ‎②保持玻璃管沿竖直方向放置，向玻璃管内缓慢注入水银,当水银柱上端与管口相平时封闭气柱的长度。答案：15 cm ‎4、（9分）如图所示，圆柱形绝热汽缸放置于水平桌面上，质量为m的活塞将一定质量的理想气体密封在汽缸中，开始时活塞距汽缸底部高度为h1=0．40 m，现缓慢将气缸倒置，稳定后活塞到汽缸底部的距离为h2= 0．60 m，已知活塞面积S=50.0cm2，取大气压强Po=l．0×l05 Pa，g=l0N/kg，不计活塞与汽缸之间的摩擦。求：‎ ‎（i）活塞的质量m; 答案：10kg ‎（ii）气体内能的变化量△U。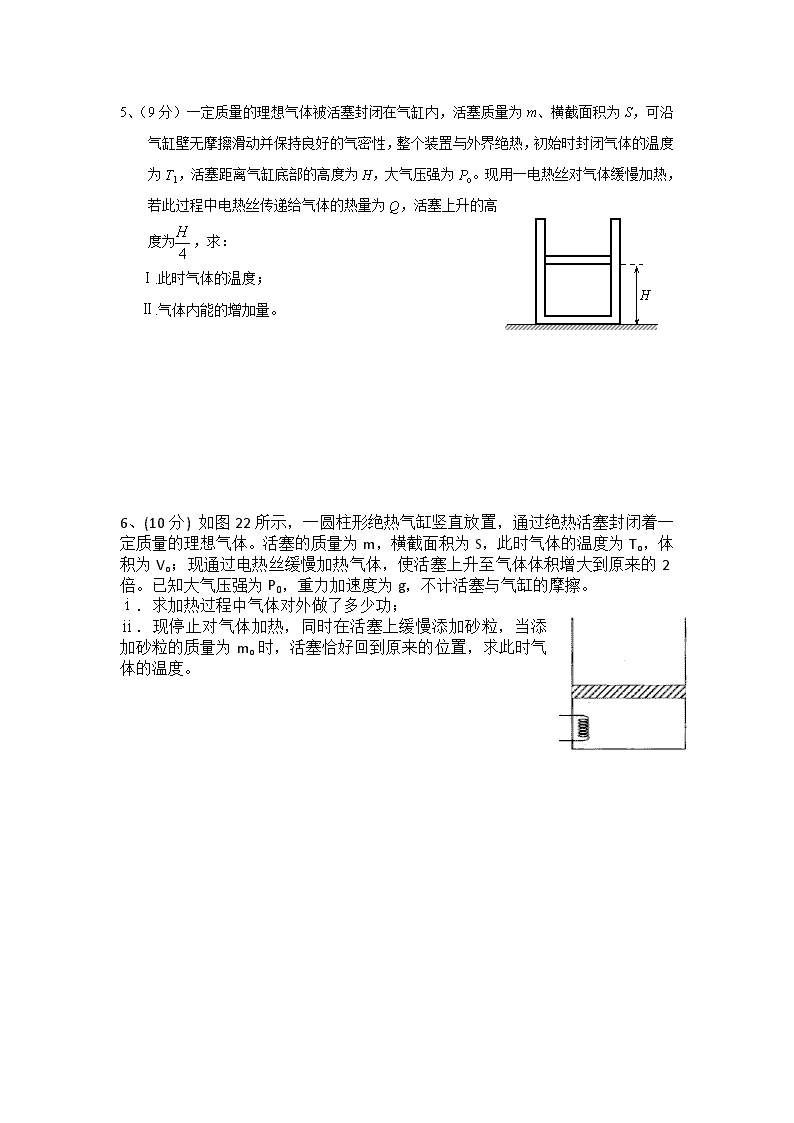答案：—80J H ‎5、（9分）一定质量的理想气体被活塞封闭在气缸内，活塞质量为m、横截面积为S，可沿气缸壁无摩擦滑动并保持良好的气密性，整个装置与外界绝热，初始时封闭气体的温度为T1，活塞距离气缸底部的高度为H，大气压强为Po。现用一电热丝对气体缓慢加热，若此过程中电热丝传递给气体的热量为Q，活塞上升的高度为，求：‎ Ⅰ.此时气体的温度；‎ Ⅱ.气体内能的增加量。‎ ‎6、(10分) 如图22所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体。活塞的质量为m，横截面积为S，此时气体的温度为To，体积为Vo；现通过电热丝缓慢加热气体，使活塞上升至气体体积增大到原来的2倍。已知大气压强为P0，重力加速度为g，不计活塞与气缸的摩擦。‎ ⅰ．求加热过程中气体对外做了多少功；‎ ⅱ．现停止对气体加热，同时在活塞上缓慢添加砂粒，当添加砂粒的质量为mo时，活塞恰好回到原来的位置，求此时气体的温度。‎ ‎ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ 计算题答案 ‎1、（2）（10分）①设玻璃管横截面积为S，以管内封闭气体为研究对象， 气体经等压膨胀：‎ ‎ 初状态：V1=51S T1=306K ‎ 末状态：V2=53S T2=？ （1分）‎ ‎ 由盖—吕萨克定律：（2分） 得T2=318K （1分）‎ ‎②当水银柱上表面与管口相平，设此时管中气体压强为P，水银柱的高度为H，管内气体经等温压缩：‎ 初状态：V1=51S P1= 80cmHg （1分）‎ 末状态：V2¢=(57-H)S P2=(76+H) cmHg （1分）‎ 由玻意耳定律：P1 V1 =P2V2¢（2分） 得 H=9cm（1分）‎ 故P2=85cmHg（1分）‎ ‎5、解：Ⅰ. 气体加热缓慢上升过程中，处于等压过程，设上升时温度为，则 ‎ ① ②‎ ‎ ③ ④‎ Ⅱ. 上升过程中，据热力学第一定律得：‎ ‎ ⑤ 式中： ⑥ ‎ ‎ 因此： ⑦ ‎ ‎ 评分标准：本题共9分。正确得出①、②、④、⑤、⑦式各1分，③、⑥式各2分。‎ ‎6、解：ⅰ.气体发生等压变化，据盖吕萨克定律可得 ‎ ① 据题意，，可得 ‎ ② 气体对外做的功： ③‎ ⅱ.未加砂子时，，， ④‎ 活塞回到原位置时，， ⑤‎ 据理想气体的状态方程可得 ‎ ⑥‎ 解得 ⑦‎