高考数学专题复习立体几何理科练习题 3页

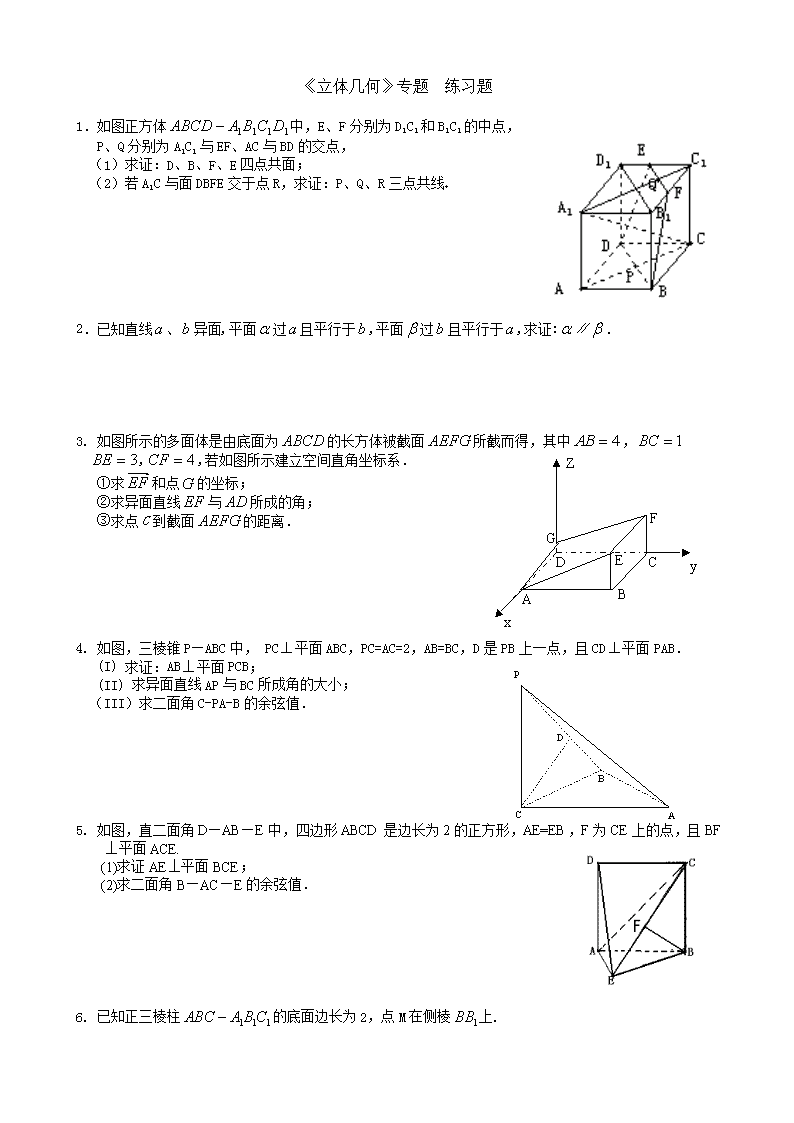
‎《立体几何》专题 练习题 ‎1．如图正方体中，E、F分别为D1C1和B1C1的中点，‎ P、Q分别为A1C1与EF、AC与BD的交点，‎ ‎（1）求证：D、B、F、E四点共面；‎ ‎（2）若A1C与面DBFE交于点R，求证：P、Q、R三点共线 ‎2．已知直线、异面,平面过且平行于,平面过且平行于,求证:∥．‎ F E C B y Z x G D A ‎3. 如图所示的多面体是由底面为的长方体被截面所截而得，其中，‎ ‎,,若如图所示建立空间直角坐标系．‎ ‎①求和点的坐标；‎ ‎②求异面直线与所成的角；‎ ‎③求点C到截面的距离．‎ ‎4. 如图，三棱锥P—ABC中， PC平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD平面PAB．‎ ‎(I) 求证：AB平面PCB；‎ ‎(II) 求异面直线AP与BC所成角的大小； ‎ ‎（III）求二面角C-PA-B的余弦值．‎ ‎5. 如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.‎ ‎(1)求证AE⊥平面BCE；‎ ‎(2)求二面角B—AC—E的余弦值．‎ ‎6. 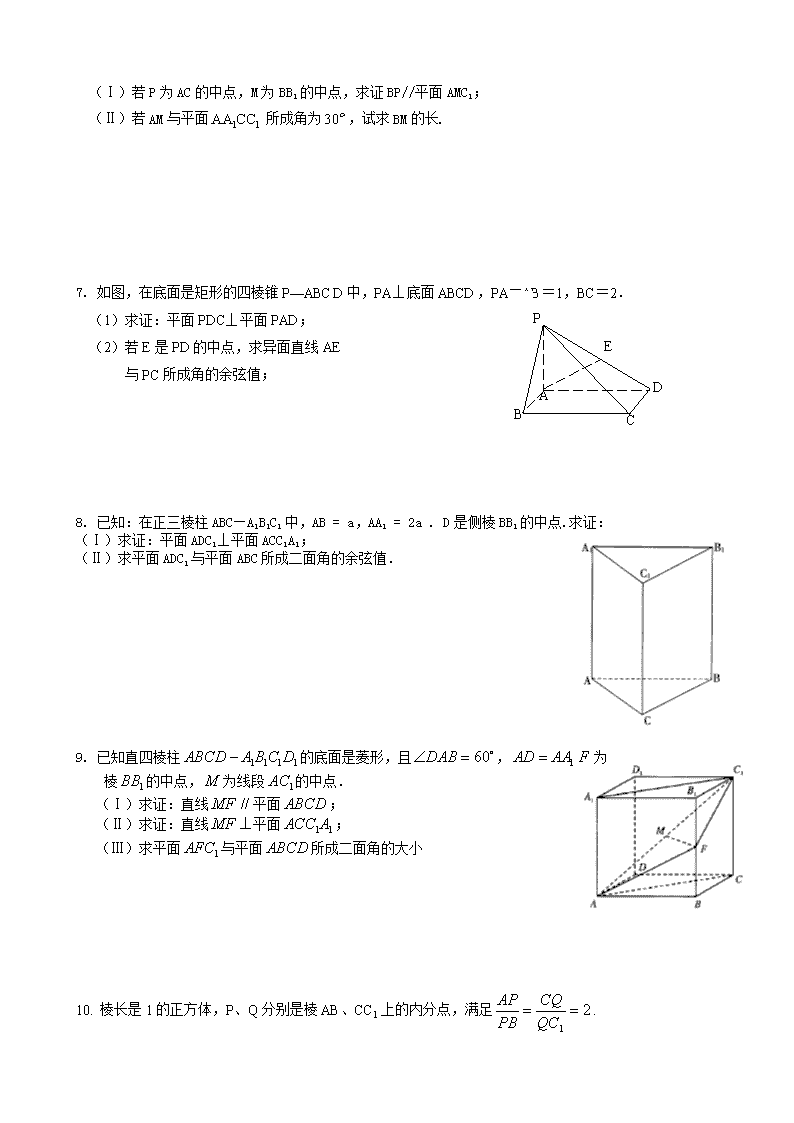已知正三棱柱的底面边长为2，点M在侧棱上.‎ ‎（Ⅰ）若P为AC的中点，M为BB1的中点，求证BP//平面AMC1；‎ ‎（Ⅱ）若AM与平面所成角为，试求BM的长.‎ P A B C D E ‎7. 如图，在底面是矩形的四棱锥P—ABCD中，PA⊥底面ABCD，PA＝AB＝1，BC＝2．‎ ‎（1）求证：平面PDC⊥平面PAD；‎ ‎（2）若E是PD的中点，求异面直线AE 与PC所成角的余弦值；‎ ‎ ‎ ‎8. 已知：在正三棱柱ABC—A1B1C1中，AB = a，AA1 = 2a . D是侧棱BB1的中点.求证：‎ ‎（Ⅰ）求证：平面ADC1⊥平面ACC1A1；‎ ‎（Ⅱ）求平面ADC1与平面ABC所成二面角的余弦值．‎ ‎ ‎ ‎9. 已知直四棱柱的底面是菱形，且，为 棱的中点，为线段的中点．‎ ‎ （Ⅰ）求证：直线平面；‎ ‎ （Ⅱ）求证：直线平面；‎ ‎ （Ⅲ）求平面与平面所成二面角的大小 ‎10. 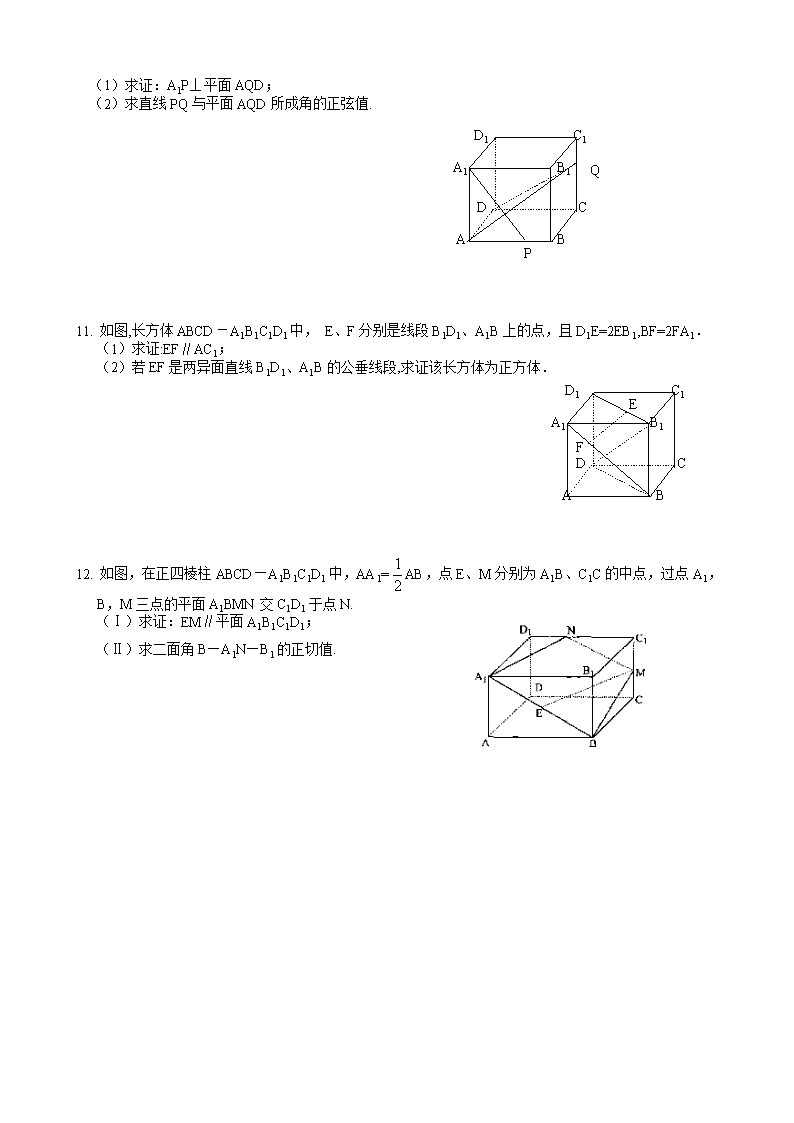棱长是1的正方体，P、Q分别是棱AB、CC1上的内分点，满足.‎ ‎（1）求证：A1P⊥平面AQD；‎ ‎（2）求直线PQ与平面AQD所成角的正弦值.‎ Q P ‎ D1 C1‎ A1 B1‎ ‎ D C A B ‎ ‎ ‎11. 如图,长方体ABCD－A1B1C1D1中， E、F分别是线段B1D1、A1B上的点，且D1E=2EB1,BF=2FA1．‎ ‎（1）求证:EF∥AC1；‎ ‎（2）若EF是两异面直线B1D1、A1B的公垂线段,求证该长方体为正方体．‎ ‎ D1 C1‎ A1 B1‎ E F ‎ D C A B ‎12. 如图，在正四棱柱ABCD—A1B1C1D1中，AA1=AB，点E、M分别为A1B、C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.‎ ‎ （Ⅰ）求证：EM∥平面A1B1C1D1；‎ ‎　 （Ⅱ）求二面角B—A1N—B1的正切值.‎