新课标数学历年高考试题汇总及详细答案解析 68页

2014 年普通高等学校招生全国统一考试 理科（新课标卷Ⅱ） 第Ⅰ卷 一.选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合 题目要求的. 1.设集合 M=｛0,1,2｝，N= 2| 3 2 0x x x  ≤ ，则 M N =( ) A. ｛1｝ B. ｛2｝ C. ｛0，1｝ D. ｛1，2｝ 【答案】D 把 M=｛0,1,2}中的数,代入不等式 ,023-2 ≤+xx 经检验 x=1,2 满足。所以选 D. 2.设复数 1z ， 2z 在复平面内的对应点关于虚轴对称， 1 2z i  ，则 1 2z z  （ ） A. - 5 B. 5 C. - 4+ i D. - 4 - i 【答案】B .,5-4-1-∴ ,2-,2 21 2211 Bzz izzziz 故选 关于虚轴对称，与 == +=∴+= 3.设向量 a,b 满足|a+b|= 10 ，|a-b|= 6 ，则 a b = ( ) A. 1 B. 2 C. 3 D. 5 【答案】A .,1 ,62-102∴,6|-|,10|| 2222 Aba babababababa 故选联立方程解得 ，， = =+=++==+ 4.钝角三角形 ABC 的面积是 1 2 ，AB=1，BC= 2 ，则 AC=( ) A. 5 B. 5 C. 2 D. 1 【答案】B ..5,cos2-4 3π∴ ΔABC4 π.4 3π,4 π∴ ,2 2sin∴ 2 1sin122 1sin2 1 222 ΔABC BbBaccabB BB BBBacS 故选解得，使用余弦定理， 符合题意，舍去。为等腰直角三角形，不时，经计算当或 =+== == ==•••== 5.某地区空气质量监测资料表明，一天的空气质量为优良的概率是 0.75， 连续两为优良的概率是 0.6，已知某天的空气质量为优良，则随后一天的 空气质量为优良的概率是（ ） A. 0.8 B. 0.75 C. 0.6 D. 0.45 【答案】 A .,8.0,75.06.0 , App p 故选解得则据题有 优良的概率为则随后一个空气质量也设某天空气质量优良， =•= 6.如图，网格纸上正方形小格的边长为 1（表示 1cm）,图中粗线画出的是某零件的三视图， 该零件由一个底面半径为 3cm，高为 6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与 原来毛坯体积的比值为（ ） A. 17 27 B. 5 9 C. 10 27 D. 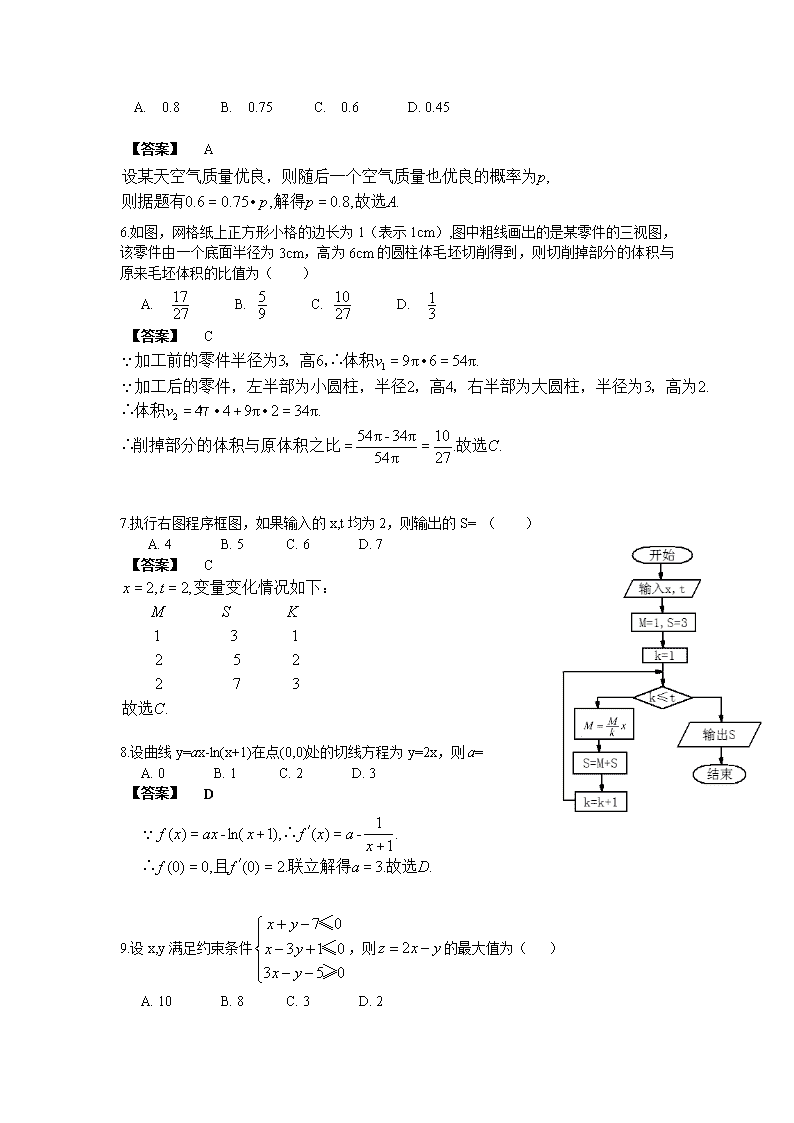1 3 【答案】 C ..27 10 π54 π34-π54 π.342π944 .2342 π.546π963 2 1 C v v 故选积之比削掉部分的体积与原体 体积 ，高为径为，右半部为大圆柱，半，高为小圆柱，半径加工后的零件，左半部 体积，，高加工前的零件半径为 ==∴ =•+•=∴ =•=∴ π   7.执行右图程序框图，如果输入的 x,t 均为 2，则输出的 S= （ ） A. 4 B. 5 C. 6 D. 7 【答案】 C . 3 7 2 2 5 2 1 3 1 ,2,2 C KSM tx 故选 变量变化情况如下：== 8.设曲线 y=ax-ln(x+1)在点(0,0)处的切线方程为 y=2x，则 a= A. 0 B. 1 C. 2 D. 3 【答案】 D ..3.2)0(,0)0( .1 1-)(),1ln(-)( Daff xaxfxaxxf 故选联立解得且 ==′=∴ +=′∴+= 9.设 x,y 满足约束条件 7 0 3 1 0 3 5 0 x y x y x y         ≤ ≤ ≥ ，则 2z x y  的最大值为（ ） A. 10 B. 8 C. 3 D. 2 【答案】 B ..8 ,)2,5(07-013--2 Bz yxyxyxz 故选取得最大值 处的交点与在两条直线 可知目标函数三角形，经比较斜率，画出区域，可知区域为 = =+=+= 10.设 F 为抛物线 C: 2 3y x 的焦点，过 F 且倾斜角为 30°的直线交 C 于 A,B 两点，O 为坐 标原点，则△OAB 的面积为（ ） A. 3 3 4 B. 9 3 8 C. 63 32 D. 9 4 【答案】 D ..4 9)(4 3 2 1 .6),3-2(2 3),32(2 33-4 322,34 322 2,2 ΔOAB DnmS nmnmnnmm nBFmAFBA 故选 ，解得 直角三角形知识可得，，则由抛物线的定义和，分别在第一和第四象限、设点 =+••=∴ =+∴=+=•=+•= == 11.直三棱柱 ABC-A1B1C1 中，∠BCA=90°，M，N 分别是 A1B1，A1C1 的中点，BC=CA=CC1， 则 BM 与 AN 所成的角的余弦值为（ ） A. 1 10 B. 2 5 C. 30 10 D. 2 2 【答案】 C ..10 30 56 41-0 |||| θcos 2-1-,0(2-1,1-(∴).0,1,0(),0,1,1(),2,0,2(),2,2,0( ,2,, 111111 C ANBM ANBM ANBMNMBA CCBCACZYXCCACBC 故选 ）。，），， 则轴，建立坐标系。令为，，如图，分别以 =+= • •= == === 12.设函数   3sin xf x m  .若存在  f x 的极值点 0x 满足   22 2 0 0x f x m    ，则 m 的 取值范围是（ ） A.    , 6 6,    B.    , 4 4,    C.    , 2 2,    D.   , 1 4,    【答案】 C .2.||,34 ∴34)]([ ,2 ||||,3)]([3πsin3)( 2 22 2 0 2 0 0 2 0 Cmmmmxfx mxxfm xxf 故选解得， ，即的极值为 ><++≥+∴ ≤=±= 第Ⅱ卷 本卷包括必考题和选考题两部分.第 13 题~第 21 题为必考题，每个试题考生必须做答. 第 22 题~第 24 题为选考题，考生根据要求做答. 二.填空题 13. 10x a 的展开式中， 7x 的系数为 15，则 a=________.(用数字填写答案) 【答案】 2 1 .2 1.2 1,15a∴15xax 33 10 7373 10 ==== aaCC 故 14.函数      sin 2 2sin cosf x x x      的最大值为_________. 【答案】 1 .1∴.1≤sin φsin)φcos(-φcos)φsin( )φcos(φsin2-φsin)φcos(φcos)φsin( )φcos(φsin2-)φ2sin()( 最大值为x xx xxx xxxf = •+•+= +•++•+= ++= 15.已知偶函数  f x 在 0, 单调递减，  2 0f  .若  1 0f x   ，则 x 的取值范围是 __________. 【答案】 ），（）， ∞3∪1-∞-( + .∞3∪1-∞-(∈2|1-| .31--(2|1-|0)1-(∴ .2||0)(∴ 0)2(),0[)( ），（），，解得故解集为 ），（），，解得的解集为 的解集为 上单增，且在偶函数 +> +∞∪∞∈>> >> =+∞= xx xxxf xxf fxfy 16.设点 M（ 0x ,1），若在圆 O: 2 2 1x y  上存在点 N，使得∠OMN=45°，则 0x 的取值范 围是________. 【答案】 ]1,1-[ ].1,1-[∈x].1,1-[x .,1)M(x1,yO 00 0 故形外角知识，可得由圆的切线相等及三角 在直线上其中和直线在坐标系中画出圆 ∈ = 三.解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分 12 分） 已知数列 na 满足 1a =1， 1 3 1n na a   . （Ⅰ）证明 1 2na  是等比数列，并求 na 的通项公式； （Ⅱ）证明： 1 2 31 1 1 2na a a  …+ . 【答案】 (1) 无 （2） 无 （1） 的等比数列。公比为是首项为 3,2 3 2 1}2 1{∴ ).2 1(32 1132 1a∴ .*N∈.n13,1 1 1n 11 =++ +=++=+ +== + + aa aa aaa n nn nn (2) （证毕），所以， ）（ 时，当 ，知，由 .*∈ 2 31111 .2 3 3 1-12 3 3 1-1 3 1-1 3 1 3 1 3 111111∴ .3 1 1-3 211,11 .1-3 21 2 1-3∴,2 3 2 1)1( 321 1-21 321 1- 1 Nnaaaa aaaa ana aaa n n n n n nn n n n n n n n <++++ <==++++<++++ <=>= ===+   18. （本小题满分 12 分） 如图，四棱锥 P-ABCD 中，底面 ABCD 为矩形，PA⊥平面 ABCD，E 为 PD 的中点. （Ⅰ）证明：PB∥平面 AEC； （Ⅱ）设二面角 D-AE-C 为 60°，AP=1，AD= 3 ，求三棱锥 E-ACD 的体积. 【答案】 (1) 无 （2） 无 （1） 设 AC 的中点为 G, 连接 EG。在三角形 PBD 中，中位线 EG//PB,且 EG 在平面 AEC 上， 所以 PB//平面 AEC. （2）设 CD=m, 分别以 AD,AB,AP 为 X,Y,Z 轴建立坐标系，则 。的体积为所以，三棱锥 的高即为三棱锥 面且的中点，则为设 解得 解得一个 则法向量为同理设平面 解得一个 则法向量为设平面 8 3- .8 3 2 132 3 2 1 3 1 3 1∴.- ,⊥,2 1 2,// .2 3,2 1 33 3 |||| |||,cos|3 πcos ).3-,3-,( ,0,0),,,( ).0,1,0( ,0,0),,,( ).0,,3(),2 1,0,2 3(),0,0,3(∴ ).0,,3(),2 1,0,2 3(),0,0,3(),0,0,0( Δ- 22 22 22 22 2 222222 1 111111 ACDE EFSVACDE ACDEFEFPAEFPAADF m mmnn nnnn mmn AEnACnzyxnACE n AEnADnzyxnADE mACAEAD mCEDA ACDACDE =••••=••= == == ++ = • •=><= = === = === ===  19. （本小题满分 12 分） 某地区 2007 年至 2013 年农村居民家庭纯收入 y（单位：千元）的数据如下表： 年份 2007 2008 2009 2010 2011 2012 2013 年份代号 t 1 2 3 4 5 6 7 人均纯收入 y 2.9 3.3 3.6 4.4 4.8 5.2 5.9 （Ⅰ）求 y 关于 t 的线性回归方程； （Ⅱ）利用（Ⅰ）中的回归方程，分析 2007 年至 2013 年该地区农村居民家庭人均纯收入的 变化情况，并预测该地区 2015 年农村居民家庭人均纯收入. 附：回归直线的斜率和截距的最小二乘法估计公式分别为：      1 2 1 n i i i n i i t t y y b t t          ， ˆˆa y bt  【答案】 (1) .3.25.0 += ty （2） 约 6800 元 （1） .3.25.0 3.24*2 1-3.4- ,2 1 2*14 14 2*)149( 8.48.15.007.0214*3 , 3.47 9.52.58.44.46.33.39.2,47 721 += === ==++ ++++++= += =++++++==+++= tyty tbya b abty yt 的回归方程为关于所以， 代入公式，经计算得设回归方程为  百元左右。千年，该区人均纯收入约所以，预计到 千元）该区人均纯收入 年，增长，预计到年该区人均纯收入稳步年至 862015 (8.63.295.0 201520132007∴,02 1 =+•= >= y b 20. （本小题满分 12 分） 设 1F , 2F 分别是椭圆  22 2 2 1 0yx a ba b    的左右焦点，M 是 C 上一点且 2MF 与 x 轴垂直， 直线 1MF 与 C 的另一个交点为 N. （Ⅰ）若直线 MN 的斜率为 3 4 ，求 C 的离心率； （Ⅱ）若直线 MN 在 y 轴上的截距为 2，且 15MN F N ，求 a,b. 【答案】 (1) 2 1 （2） 72,7 == ba （1） .2 1∴.2 1 02-32.,4 3 2 1∴ 4 3 2222 2 21 1 的离心率为解得 ，联立整理得：且由题知， Ce eecbaca b FF MF = =++==•= （2） 72,7 .72,7. ,,1:4:)2 3-(, :.2 3-,, .4, .422 222 1111 11 2 2 == ==+= ==+=+= == =•= ba bacba a ceNFMFceaNFecaMF ccNM mMFmNF a bMF 所以， 联立解得 ，且 由焦半径公式可得两点横坐标分别为 可得由两直角三角形相似，由题可知设 ，即知，由三角形中位线知识可 21. （本小题满分 12 分） 已知函数  f x = 2x xe e x  （Ⅰ）讨论  f x 的单调性； （Ⅱ）设      2 4g x f x bf x  ，当 0x  时，   0g x  ,求b 的最大值； （Ⅲ）已知1.4142 2 1.4143  ，估计 ln2 的近似值（精确到 0.001） 【答案】 （1） .)( .02-12≥2-12-)(∴∈2--)( -- 上单增在所以， ， Rxf eeeeeexfRxxeexf x x x xxxxx =•+=+=′= （2） 2≥22≥ 0-0≥)-(-))((0≥)-(2-2-2 .0≥)(0,tt),(0,∈∃x∴)-(2-2-2)( .0)0(,0mm),(0,∈x)2-(2-2-)( .0≥)2-(2-2- 0≥)2-(4-4-22 .0≥)(0,mm),(0,∈∃x∴)2-(4-4-22)( .0)0(,0),2--(4-4--)( .0,0)2--(4-4--)(4-)2()( --- -----2-2 -2-2 -2-2 -2-2 -2-2 -2-2 -2-2 -2-2 的最大值为，所以，即即 ，且，即即 使， 则，同理，令 即 即 使， 则令 bbeeeebee eeeebeeeeeebee xmeebeexm meebeexm eebee eebee xheebeexh hxxeebxeexh xxeebxeexbfxfxg xxxxxx xxxxxxxxxxxx xxxx xxxx xxxx xxxx xxxx xxxx xxxx =•>++ >+ >=′ =>++= ++ ++ ′>++=′ =>= >>== （3） .2 22ln4 1-23 2.4 1-23 22ln2 3-242ln6 ),2ln2- 2 1-282ln2-2 1-2)2(ln8)2(ln )2(ln8)2ln2(,02ln),(8)2()2(.2 22ln .02ln-2 22ln2- 2 1-2)2(ln,0)2(ln,02ln <<>> >> >>=>< >==>>= 所以，即 解得（，即即 ，则令知，由解得 即则设 ff ffxxfxf ffx 请考生在第 22、23、24 题中任选一题做答，如果多做，同按所做的第一题计分，做答时请 写清题号. 22.（本小题满分 10）选修 4—1：几何证明选讲 如图，P 是  O 外一点，PA 是切线，A 为切点，割线 PBC 与  O 相交于 点 B，C，PC=2PA，D 为 PC 的中点，AD 的延长线交  O 于点 E.证明： （Ⅰ）BE=EC； （Ⅱ）AD DE=2 2PB 【答案】 (1) 无 （2）无 （1） EC.BEBE∠CE∠BE∠αBE,∠βαβ BE∠∠DEB∠PDA∠∠∠∠∠ .AE∠CE,∠EB∠, ,,2 ===+=+∴ +===+=+ ====∠ Δ=∴== ，所以，即即 则连接 为等腰三角形。， DBDD DPADBADPABBCEPAB BBDPABAB PADPDPADCPDPAPC   αβ （2） 2 2 2PA PA-PAPB-PB)PA-(PADCBD ,,PADC,BDDEAD PBPBPBPB PCPBPCPB PADCPDPCPB =•=• •=••==•∴ ==•=•=• ）（  23. （本小题满分 10）选修 4-4：坐标系与参数方程 在直角坐标系 xoy 中，以坐标原点为极点，x 轴为极轴建立极坐标系，半圆 C 的极坐标方程 为 2cos  ， 0, 2       . （Ⅰ）求 C 的参数方程； （Ⅱ）设点 D 在 C 上，C 在 D 处的切线与直线 : 3 2l y x  垂直，根据（Ⅰ）中你得到 的参数方程，确定 D 的坐标. 所以 D 点坐标为 3 1(1 , )2 2  或 3 1(1 , )2 2   。 24. （本小题满分 10）选修 4-5：不等式选讲 设函数  f x = 1 ( 0)x x a aa    （Ⅰ）证明：  f x ≥2； （Ⅱ）若  3 5f  ，求 a 的取值范围. 2014 年普通高等学校招生全国统一考试全国理科数学 1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答题前，考生务必将自己的 姓名、准考证号填写在答题卡上. 2.回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需 改动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效. 3. 回答第Ⅱ卷时，将答案写在答题卡上，答在本试题上无效. 4. 考试结束，将本试题和答题卡一并交回. 第Ⅰ卷 一．选择题：共 12 小题，每小题 5 分，共 60 分。在每个小题给出的四个选项中，只有一项 是符合题目要求的一项。 1.已知集合 A={ x | 2 2 3 0x x   }，B={ x |－2≤ x ＜2｝，则 A B = A .[-2,-1] B .[-1,2） C .[-1,1] D .[1,2） 答案：A 2. 3 2 (1 ) (1 ) i i   = A .1 i B .1 i C . 1 i  D . 1 i  答案：D 3.设函数 ( )f x ， ( )g x 的定义域都为 R，且 ( )f x 是奇函数， ( )g x 是偶函数，则下列结论正 确的是 A . ( )f x ( )g x 是偶函数 B .| ( )f x | ( )g x 是奇函数 C . ( )f x | ( )g x |是奇函数 D .| ( )f x ( )g x |是奇函数 答案：C 4.已知 F 是双曲线C ： 2 2 3 ( 0)x my m m   的一个焦点，则点 F 到C 的一条渐近线的距 离为 A . 3 B .3 C . 3m D .3m 答案：A 5.4 位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公 益活动的概率 A . 1 8 B . 3 8 C . 5 8 D . 7 8 答案：D 6.如图，圆 O 的半径为 1，A 是圆上的定点，P 是圆上的动点，角 x 的始边为射线OA ， 终边为射线OP ，过点 P 作直线OA的垂线，垂足为 M ，将点 M 到直线OP 的距 离表示为 x 的函数 ( )f x ，则 y = ( )f x 在[0, ]上的图像大致为 答案： 1( ) | cos sin | | sin 2 |2f x x x x  。选 C 7.执行下图的程序框图，若输入的 , ,a b k 分别为 1,2,3，则输出的 M = A . 20 3 B .16 5 C . 7 2 D .15 8 答案：D 8.设 (0, )2   ， (0, )2   ，且 1 sintan cos    ，则 A .3 2    B . 2 2    C .3 2    D . 2 2    答案： 1 cos( )1 sin 12 tancos sin( ) tan2 4 2                 ， 又因 (0, )2   ， (0, )2   ，所以 4 2 2       ，变形后选 B. 9.不等式组 1 2 4 x y x y      的解集记为 D .有下面四个命题： 1p ： ( , ) , 2 2x y D x y     ， 2p ： ( , ) , 2 2x y D x y    , 3p ： ( , ) , 2 3x y D x y    ， 4p ： ( , ) , 2 1x y D x y     . 其中真命题是 A . 2p ， 3p B . 1p ， 4p C . 1p ， 2p D . 1p ， 3p 答案：C 10.已知抛物线C ： 2 8y x 的焦点为 F ，准线为l ，P 是l 上一点，Q 是直线 PF 与C 的一 个交点，若 4FP FQ  ，则| |QF = A . 7 2 B . 5 2 C .3 D .2 答案：D 11.已知函数 ( )f x = 3 23 1ax x  ， 若 ( )f x 存在唯一的零点 0x ，且 0x ＞0，则 a 的取值范围为 A .（2，+∞） B .（-∞，-2） C .（1，+∞） D .（-∞，-1） 答案：取 a=2,研究 ( )f x 的性质后知 ( )f x 有两个零点不符合题意，故排除 C; 取 a=3,则 ( )f x 有唯一零点，但零点小于 0，故排除 A； 取 2a   时 ( )f x 有两个零点，故排除 D。 于是选 B。 12.如图，网格纸上小正方形的边长为 1，粗实线画出的是某多面体的三视图，则该多面体的 六条棱中，最长的棱的长度为 A . 6 2 B . 4 2 C .6 D .4 答案：该多面体是一个三棱锥 S—ABC，其中底 面 ABC 为等腰三角形，AC=BC= 2 5 ,AB=4， 侧棱 SA 垂直底面 ABC,且 SA=4.于是可算出最 长棱长为 SB=SC=6. 第Ⅱ卷 本卷包括必考题和选考题两个部分。第（13）题-第（21）题为必考题，每个考生都必须作 答。第（22）题-第（24）题为选考题，考生根据要求作答。 二．填空题：本大题共四小题，每小题5分。 13. 8( )( )x y x y  的展开式中 2 7x y 的系数为 .(用数字填写答案) 答案：-20. 14.甲、乙、丙三位同学被问到是否去过 A，B，C 三个城市时， 甲说：我去过的城市比乙多，但没去过 B 城市； 乙说：我没去过 C 城市； 丙说：我们三人去过同一个城市. 由此可判断乙去过的城市为 . 答案：三人必定都去过 A 城，故可判断乙去过 A 城。 15.已知 A，B，C 是圆 O 上的三点，若 1 ( )2AO AB AC    ，则 AB  与 AC  的夹角为 . 答案：90 。 16.已知 , ,a b c 分别为 ABC 的三个内角 , ,A B C 的对边， a =2，且 (2 )(sin sin ) ( )sinb A B c b C    ，则 ABC 面积的最大值为 . 答案： 3 。 三.解答题：解答应写出文字说明，证明过程或演算步骤。 17.(本小题满分 12 分)已知数列{ na }的前 n 项和为 nS ， 1a =1， 0na  ， 1 1n n na a S   ， 其中  为常数. (Ⅰ)证明： 2n na a    ； （Ⅱ）是否存在  ，使得{ na }为等差数列？并说明理由. 证明：（1） 1 1n n na a S   ① ∴ 1 2 1 1n n na a S    ② ∴由②-①得 1 2 1( )n n n na a a a    ∵ *0,na n N  ∴ 1 0na   所以 2n na a    。 （Ⅱ）假设{ na }为等差数列，公差为 d,则 21 ; (1 )2 2n n d da dn d S n n      因为 1 1n n na a S   对 *n N 恒成立，所以 2( 1 )( 1) (1 ) 12 2 d ddn d dn n n        对 *n N 恒成立 即 2 2 2(2 ) 1 (1 ) 12 2 d dd n d d n d n n         对 *n N 恒成立 则 2 2 (2 ) (1 )2 1 1 dd dd d d              解得 4 2d     所以存在 2  使得{ na }为等差数列。 18. (本小题满分 12 分)从某企业的某种产品中抽取 500 件，测量这些产品的一项质量指标值， 由测量结果得如下频率分布直方 图： (Ⅰ)求这 500 件产品质量指标值 的样本平均数 x 和样本方差 2s （同一组数据用该区间的中点值 作代表）； （Ⅱ）由频率分布直方图可以认 为，这种产品的质量指标值 Z 服从正态分布 2( , )N   ，其中  近似为样本平均数 x ， 2 近 似为样本方差 2s . (i)利用该正态分布，求 (187.8 212.2)P Z  ； （ii）某用户从该企业购买了 100 件这种产品，记 X 表示这 100 件产品中质量指标值为于区 间（187.8,212.2）的产品件数，利用（i）的结果，求 EX . 附： 150 ≈12.2. 若 Z ～ 2( , )N   ，则 ( )P Z       =0.6826， ( 2 2 )P Z       =0.9544. 解：（1） 170 0.02 180 0.09 190 0.22 200 0.33 210 0.24 220 0. 08 230 0.02 200x                2 2 2 2 2 2 230 0.02 20 0.09 10 0.22 0 0.33 10 0.24 20 0.08 30 0.0 2 150s                （Ⅱ）(i)由（1）知 200, 150 12.2    ，所以 (187.8 212.2)P Z  =0.6828 （ii）由已知得 (100,0.6828)X B ，于是 100*0.6828 68.28EX   19. (本小题满分 12 分)如图三棱锥 1 1 1ABC A B C 中，侧面 1 1BB C C 为菱形， 1AB B C . (Ⅰ) 证明： 1AC AB ； （Ⅱ）若 1AC AB ， o 1 60CBB  ，AB=BC，求二面 角 1 1 1A A B C  的余弦值. 解：（Ⅰ）因为侧面 1 1BB C C 为菱形， 所以 1 1B C BC ，设垂足为 O，则点 O 为 1B C 的中点。 又因 1B C AB ，所以 1B C  平面 AB 1C , 而OA 在平面 AB 1C 内，于是有 1B C OA 于是 AC= 1AB . (Ⅱ）在菱形 1 1BB C C 中 o 1 60CBB  ，则有 1BB C 为等边三角形，设 BC=2,则 OC=1,OB= 3 . 在 1ACB 中， 1AC AB ， 1AC AB ， 1CB =2,所以 OA=1 又因 AB=BC=2,所以 AOB 为直角三角形，OA OB 又因 OB 1OB ， 1OA OB ，于是可以 OB,O 1B ,OA 为 x,y,z 轴建立空间直角坐标系，则 A(0,0,1), 1(0,1,0)B ， 1( 3,0,0)C  ，C(0, 1,0) , 因为 1 1AA CC  于是 1( 3,1,1)A  。 平面 1 1AA B 的法向量 (1, 3, 3)m  ，平面 1 1 1A B C 的法向量为 (1, 3, 3)n   于是法向量夹角余弦为 1 7 。 由于二面角 1 1 1A A B C  为锐角，所以二面角 1 1 1A A B C  的余弦为 1 7 。 20. (本小题满分 12 分) 已知点 A（0，-2），椭圆 E ： 2 2 2 2 1( 0)x y a ba b     的离心率为 3 2 ， F 是椭圆的焦点，直线 AF 的斜率为 2 3 3 ，O 为坐标原点. (Ⅰ)求 E 的方程； （Ⅱ）设过点 A 的直线l 与 E 相交于 ,P Q 两点，当 OPQ 的面积最大时，求l 的方程. 解：(Ⅰ)由椭圆 E 的离心率为 3 2 得 3 2 c a  。 因为直线 AF 的斜率为 2 3 3 ，且 (0, 2), ( ,0)A F c 得 2 2 3 3c  ，所以 c= 3 。 于是 a=2,b=1,椭圆 E 的方程为 2 2 14 x y  （Ⅱ）设直线l 的方程为 ( 2)x m y  ， 1 1 2 2( , ), ( , )P x y Q x y 由方程组 2 24 4 ( 2) x y x m y       得 2 2 2 2(4 ) 4 4 4 0m y m y m     则有 2 2 1 2 1 22 2 4 4( 1),4 4 m my y y ym m      于是 4 2 2 2 1 2 2 2 2 2 2 16 16( 1) 16| | (4 3 )(4 ) 4 (4 ) m my y mm m m        而 2 1 2 2 1 4 | || 2 || | 4 32 4OPQ mS m y y mm     2 2 4 34 ,( 4) t t t   其中 2t m 设 2 2 4 3( ) ( 4) t tg t t   ，利用判别式法，求出 ( )g t 的最大值是 4( )7g = 1 16 ， 于是 OPQS 的最大值为 1 4 ，且此时 2 7 m   ，直线 l 的方程为 7 22y x  或 7 22y x   。 21. (本小题满分 12 分)设函数 1 ( ) ln x x bef x ae x x    ，曲线 ( )y f x 在点（1， (1)f 处的 切线为 ( 1) 2y e x   . (Ⅰ)求 ,a b ； （Ⅱ）证明： ( ) 1f x  . 解：（1）由已知得 (1) 2 '(1) f f e    而 1 2 1'( ) ln ( 1) x x x bef x ae x ae xx x      于是 2 1 b a    （Ⅱ）由(Ⅰ)得 12( ) ln x x ef x e x x    ，要证 ( ) 1f x  需证 1ln 2x xxe x e x  需证： 2ln x xx x e e   设 2( ) lng x x x e   ， ( ) x xh x e  利用导数研究两函数性质，知 ( )g x 在 (0, ) 上存在最小值 1( )g e  1 e ; ( )h x 在 (0, ) 上存在最大值 (1)h  1 e 于是在 (0, ) 上必定有 ( ) ( )g x h x 恒成立 于是 ( ) 1f x  点评：化复杂函数为简单函数，是我们处理这一问题的关键。 请考生从第（22）、（23）、（24）三题中任选一题作答。注意：只能做所选定的题目。如果 多做，则按所做的第一个题目计分，作答时请用 2B 铅笔在答题卡上将所选题号后的 方框 涂黑。 22.（本小题满分 10 分）选修 4—1：几何证明选讲 如图，四边形 ABCD 是⊙O 的内接四边形，AB 的延长线与 DC 的 延长线交于点 E，且 CB=CE .(Ⅰ)证明：∠D=∠E； （Ⅱ）设 AD 不是⊙O 的直径，AD 的中点为 M，且 MB=MC，证明：△ADE 为等边三角形. 答案：.(Ⅰ) ∠D=∠CBE=∠E (2)利用 AMB DMC   可证∠D==∠A=∠E,从而得出△ADE 为等边三角形. 23. （本小题满分 10 分）选修 4—4：坐标系与参数方程 已知曲线C ： 2 2 14 9 x y  ，直线l ： 2 2 2 x t y t      （t 为参数）. (Ⅰ)写出曲线C 的参数方程，直线l 的普通方程； （Ⅱ）过曲线C 上任一点 P 作与l 夹角为 o30 的直线，交l 于点 A ，求| |PA 的最大值与最小 值. 答案：（1）曲线 C 的参数方程为 2cos 3sin x y      ，其中 为参数。 直线 l 的普通方程为： 2 6 0x y   （（Ⅱ）设点 P (2cos ,3sin )  ，点 P 到直线 l 的距离为 d，则 | 4cos 3sin 6 || | 2 2 5 PA d     设 ( ) 4cos 3sin 6, [0,2 ]f         由 ( )f  的值域为[ 11, 1]  ，于是| |PA 的最大值为 22 5 ，最小值为 2 5 。 24. （本小题满分 10 分）选修 4—5：不等式选讲 若 0, 0a b  ，且 1 1 aba b   . (Ⅰ) 求 3 3a b 的最小值； （Ⅱ）是否存在 ,a b ，使得 2 3 6a b  ？并说明理由. 解：(Ⅰ)由 1 1 aba b   得 a b ab ab  ,而 2a b ab  ，所以 2ab  当且仅当 2a b  时取等号。 而 3 3 2 4 2a b ab ab   当且仅当 2a b  时取等号 于是 3 3a b 的最小值为 4 2 （Ⅱ）因为 0, 0a b  ，所以 2 3 2 6 4 3 6a b ab    于是不能存在 ,a b ，使得 2 3 6a b  。 2013 年普通高等学校数学(全国新课标卷 II) 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只 有一项是符合题目要求的． 1．(2013 课标全国Ⅱ，理 1)已知集合 M＝{x|(x－1)2＜4，x∈R}，N ＝{－1,0,1,2,3}，则 M∩N＝( )． A．{0,1,2} B．{－1,0,1,2} C．{－1,0,2,3} D．{0,1,2,3} 2．(2013 课标全国Ⅱ，理 2)设复数 z 满足(1－i)z＝2i，则 z＝( )． A．－1＋i B．－1－I C．1＋i D．1－i 3．(2013 课标全国Ⅱ，理 3)等比数列{an}的前 n 项和为 Sn.已知 S3＝ a2＋10a1，a5＝9，则 a1＝( )． A． 1 3 B． 1 3  C． 1 9 D． 1 9  4．(2013 课标全国Ⅱ，理 4)已知 m，n 为异面直线，m⊥平面α，n ⊥平面β.直线 l 满足 l⊥m，l⊥n，l α，l β，则( )． A．α∥β且 l∥α B．α⊥β且 l⊥β C．α与β相交，且交线垂直于 l D．α与β相交，且 交线平行于 l 5．(2013 课标全国Ⅱ，理 5)已知(1＋ax)(1＋x)5 的展开式中 x2 的系数为 5，则 a＝( )． A．－4 B．－3 C．－2 D．－1 6．(2013 课标全国Ⅱ，理 6)执行下面的程序框图，如果输入的 N ＝10，那么输出的 S＝( )． A． 1 1 11+ 2 3 10    B． 1 1 11+ 2! 3! 10!    C． 1 1 11+ 2 3 11    D． 1 1 11+ 2! 3! 11!    7．(2013 课标全国Ⅱ，理 7)一个四面体的顶点在空间直角坐标系 O －xyz 中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该 四面体三视图中的正视图时，以 zOx 平面为投影面，则得到的正视图 可以为( )． 8．(2013 课标全国Ⅱ，理 8)设 a＝log36，b＝log510，c＝log714，则 ( )． A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b ＞c 9．(2013 课标全国Ⅱ，理 9)已知 a＞0，x，y 满足约束条件 1, 3, 3 . x x y y a x          若 z＝2x＋y 的最小值为 1，则 a＝( )． A． 1 4 B． 1 2 C．1 D．2 10．(2013 课标全国Ⅱ，理 10)已知函数 f(x)＝x3＋ax2＋bx＋c，下 列结论中错误的是( )． A． x0∈R，f(x0)＝0 B．函数 y＝f(x)的图像是中心对称图形 C．若 x0 是 f(x)的极小值点，则 f(x)在区间(－∞，x0)单调递减 D．若 x0 是 f(x)的极值点，则 f′(x0)＝0 11．(2013 课标全国Ⅱ，理 11)设抛物线 C：y2＝2px(p＞0)的焦点为 F，点 M 在 C 上，|MF|＝5，若以 MF 为直径的圆过点(0,2)，则 C 的方 程为( )． A．y2＝4x 或 y2＝8x B．y2＝2x 或 y2＝8x C．y2＝4x 或 y2＝16x D．y2＝2x 或 y2＝16x 12．(2013 课标全国Ⅱ，理 12)已知点 A(－1,0)，B(1,0)，C(0,1)， 直线 y＝ax＋b(a＞0)将△ABC 分割为面积相等的两部分，则 b 的取值 范围是( )． A．(0,1) B． 2 11 ,2 2      C． 2 11 ,2 3     D． 1 1,3 2     第Ⅱ卷 本卷包括必考题和选考题两部分，第 13 题～第 21 题为必考题，每个 试题考生都必须做答。第 22 题～第 24 题为选考题，考生根据要求做 答。 二、填空题：本大题共 4 小题，每小题 5 分． 13．(2013 课标全国Ⅱ，理 13)已知正方形 ABCD 的边长为 2，E 为 CD 的中点，则 AE BD  ＝__________. 14．(2013 课标全国Ⅱ，理 14)从 n 个正整数 1,2，…，n 中任意 取出两个不同的数，若取出的两数之和等于 5 的概率为 1 14 ，则 n＝ __________. 15．(2013 课标全国Ⅱ，理 15)设θ为第二象限角，若 π 1tan 4 2      ， 则 sin θ＋cos θ＝__________. 16．(2013 课标全国Ⅱ，理 16)等差数列{an}的前 n 项和为 Sn，已 知 S10＝0，S15＝25，则 nSn 的最小值为__________． 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．(2013 课标全国Ⅱ，理 17)(本小题满分 12 分)△ABC 的内角 A，B， C 的对边分别为 a，b，c，已知 a＝bcos C＋csin B. (1)求 B； (2)若 b＝2，求△ABC 面积的最大值． 18．(2013 课标全国Ⅱ，理 18)(本小题满分 12 分)如图，直三棱柱 ABC－A1B1C1 中，D，E 分别是 AB，BB1 的中点，AA1＝AC＝CB ＝ 2 2 AB . (1)证明：BC1∥平面 A1CD； (2)求二面角 D－A1C－E 的正弦值． 19．(2013 课标全国Ⅱ，理 19)(本小题满分 12 分)经销商经 销某种农产品，在一个销售季度内，每售出 1 t 该产品获利 润 500 元，未售出的产品，每 1 t 亏损 300 元．根据历史资料，得到 销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一 个销售季度购进了 130 t 该农产品．以 X(单位：t,100≤X≤150)表 示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季 度内经销该农产品的利润． (1)将 T 表示为 X 的函数； (2)根据直方图估计利润 T 不少于 57 000 元 的概率； (3)在直方图的需求量分组中，以各组的区 间中点值代表该组的各个值，并以需求量落 入该区间的频率作为需求量取该区间中点 值的概率(例如：若需求量 X∈[100,110)，则取 X＝105，且 X＝105 的概率等于需求量落入[100,110)的频率)，求 T 的数学期望． 20．(2013 课标全国Ⅱ，理 20)(本小题满分 12 分)平面直角坐标系 xOy 中，过椭圆 M： 2 2 2 2 =1x y a b  (a＞b＞0)右焦点的直线 3 0x y   交 M 于 A，B 两点，P 为 AB 的中点，且 OP 的斜率为 1 2 . (1)求 M 的方程； (2)C，D 为 M 上两点，若四边形 ACBD 的对角线 CD⊥AB，求四边形 ACBD 面积的最大值． 21．(2013 课标全国Ⅱ，理 21)(本小题满分 12 分)已知函数 f(x)＝ ex－ln(x＋m)． (1)设 x＝0 是 f(x)的极值点，求 m，并讨论 f(x)的单调性； (2)当 m≤2 时，证明 f(x)＞0. 请考生在第 22、23、24 题中任选择一题作答，如果多做，则按所做 的第一题计分，做答时请写清题号． 22．(2013 课标全国Ⅱ，理 22)(本小题满分 10 分)选修 4—1：几何 证明选讲 如图，CD 为△ABC 外接圆的切线，AB 的延长线交直线 CD 于点 D，E， F 分别为弦 AB 与弦 AC 上的点，且 BC·AE＝DC·AF，B，E，F，C 四 点共圆． (1)证明：CA 是△ABC 外接圆的直径； (2)若 DB＝BE＝EA，求过 B，E，F，C 四点的圆的面积与△ABC 外接圆 面积的比值． 23．(2013 课标全国Ⅱ，理 23)(本小题满分 10 分)选修 4—4：坐标 系与参数方程 已知动点 P，Q 都在曲线 C： 2cos , 2sin x t y t    (t 为参数)上，对应参数分别 为 t＝α与 t＝2α(0＜α＜2π)，M 为 PQ 的中点． (1)求 M 的轨迹的参数方程； (2)将 M 到坐标原点的距离 d 表示为α的函数，并判断 M 的轨迹是否 过坐标原点． 24．(2013 课标全国Ⅱ，理 24)(本小题满分 10 分)选修 4—5：不等 式选讲 设 a，b，c 均为正数，且 a＋b＋c＝1，证明： (1)ab＋bc＋ac≤ 1 3 ； (2) 2 2 2 1a b c b c a    . 2013 年普通高等学校数学(全国新课标卷 II) 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个 选项中，只有一项是符合题目要求的． 1． 答案：A 解析：解不等式(x－1)2＜4，得－1＜x＜3，即 M＝{x|－1＜x＜3}．而 N＝{－1,0,1,2,3}，所以 M∩N＝{0,1,2}，故选 A. 2． 答案：A 解析： 2i 2i 1 i=1 i 1 i 1 iz         ＝ 2 2i 2   ＝－1＋i. 3． 答案：C 解析：设数列{an}的公比为 q，若 q＝1，则由 a5＝9，得 a1＝9，此时 S3＝27，而 a2＋10a1＝99，不满足题意，因此 q≠1. ∵q≠1 时，S3＝ 3 1(1 ) 1 a q q   ＝a1·q＋10a1， ∴ 31 1 q q   ＝q＋10，整理得 q2＝9. ∵a5＝a1·q4＝9，即 81a1＝9，∴a1＝ 1 9 . 4． 答案：D 解析：因为 m⊥α，l⊥m，l α，所以 l∥α.同理可得 l∥β. 又因为 m，n 为异面直线，所以α与β相交，且 l 平行于它们的交线．故 选 D. 5． 答案：D 解析：因为(1＋x)5 的二项展开式的通项为 5Cr rx (0≤r≤5，r∈Z)，则 含 x2 的项为 2 2 5C x ＋ax· 1 5C x ＝(10＋5a)x2，所以 10＋5a＝5，a＝－1. 6． 答案：B 解析：由程序框图知，当 k＝1，S＝0，T＝1 时，T＝1，S＝1； 当 k＝2 时， 1 2T  ， 1=1+ 2S ； 当 k＝3 时， 1 2 3T   ， 1 11+ 2 2 3S    ； 当 k＝4 时， 1 2 3 4T    ， 1 1 11+ 2 2 3 2 3 4S      ；…； 当 k＝10 时， 1 2 3 4 10T      ， 1 1 11+ 2! 3! 10!S     ，k 增加 1 变为 11，满足 k＞N，输出 S，所以 B 正确． 7． 答案：A 解析：如图所示，该四面体在空间直角坐标系 O－xyz 的图像为下图： 则它在平面 zOx 上的投影即正视图为 ，故选 A. 8． 答案：D 解析：根据公式变形， lg6 lg 21lg3 lg3a    ， lg10 lg 21lg5 lg5b    ， lg14 lg 21lg7 lg7c    ， 因为 lg 7＞lg 5＞lg 3，所以 lg 2 lg 2 lg 2 lg7 lg5 lg3   ，即 c＜b＜a.故选 D. 9． 答案：B 解析：由题意作出 1, 3 x x y     所表示的区域如图阴影 部分所示， 作直线 2x＋y＝1，因为直线 2x＋y＝1 与直线 x ＝1 的交点坐标为(1，－1)，结合题意知直线 y＝a(x－3)过点(1，－ 1)，代入得 1 2a  ，所以 1 2a  . 10． 答案：C 解析：∵x0 是 f(x)的极小值点，则 y＝f(x)的图像大致如下图所示， 则在(－∞，x0)上不单调，故 C 不正确． 11． 答案：C 解析：设点 M 的坐标为(x0，y0)，由抛物线的定义，得|MF|＝x0＋ 2 p ＝ 5，则 x0＝5－ 2 p . 又点 F 的坐标为 ,02 p     ，所以以 MF 为直径的圆的方程为(x－x0) 2 px    ＋(y－y0)y＝0. 将 x＝0，y＝2 代入得 px0＋8－4y0＝0，即 2 0 2 y －4y0＋8＝0，所以 y0 ＝4. 由 2 0y ＝2px0，得16 2 5 2 pp     ，解之得 p＝2，或 p＝8. 所以 C 的方程为 y2＝4x 或 y2＝16x.故选 C. 12． 答案：B 第Ⅱ卷 本卷包括必考题和选考题两部分，第 13 题～第 21 题为必考题，每个 试题考生都必须做答。第 22 题～第 24 题为选考题，考 生根据要求做答。 二、填空题：本大题共 4 小题，每小题 5 分． 13．答案：2 解析：以 AB 所在直线为 x 轴，AD 所在直线为 y 轴建立 平面直角坐标系，如图所示，则点 A 的坐标为(0,0)， 点 B 的坐标为(2,0)，点 D 的坐标为(0,2)，点 E 的坐标 为(1,2)，则 AE  ＝(1,2)，BD  ＝(－2,2)，所以 2AE BD   . 14．答案：8 解析：从 1,2，…，n 中任取两个不同的数共有 2Cn 种取法，两数之和 为 5 的有(1,4)，(2,3)2 种，所以 2 2 1 C 14n  ，即 2 4 1 1 1 14 2 n n n n        ， 解得 n＝8. 15．答案： 10 5  解析：由 π 1 tan 1tan 4 1 tan 2          ，得 tan θ＝ 1 3  ，即 sin θ＝ 1 3  cos θ. 将其代入 sin2θ＋cos2θ＝1，得 210 cos 19   . 因为θ为第二象限角，所以 cos θ＝ 3 10 10  ，sin θ＝ 10 10 ，sin θ ＋cos θ＝ 10 5  . 16．答案：－49 解析：设数列{an}的首项为 a1，公差为 d，则 S10＝ 1 10 910 2a d＋ ＝10a1 ＋45d＝0，① S15＝ 1 15 1415 2a d ＝15a1＋105d＝25.② 联立①②，得 a1＝－3， 2 3d  ， 所以 Sn＝ 2( 1) 2 1 103 2 3 3 3 n nn n n     . 令 f(n)＝nSn，则 3 21 10( ) 3 3f n n n  ， 2 20'( ) 3f n n n  . 令 f′(n)＝0，得 n＝0 或 20 3n  . 当 20 3n  时，f′(n)＞0, 200< < 3n 时，f′(n)＜0，所以当 20 3n  时，f(n) 取最小值，而 n∈N＋，则 f(6)＝－48，f(7)＝－49，所以当 n＝7 时， f(n)取最小值－49. 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17． 解：(1)由已知及正弦定理得 sin A＝sin Bcos C＋sin Csin B．① 又 A＝π－(B＋C)，故 sin A＝sin(B＋C)＝sin Bcos C＋cos Bsin C．② 由①，②和 C∈(0，π)得 sin B＝cos B， 又 B∈(0，π)，所以 π 4B  . (2)△ABC 的面积 1 2sin 2 4S ac B ac  . 由已知及余弦定理得 4＝a2＋c2－ π2 cos 4ac . 又 a2＋c2≥2ac，故 4 2 2 ac   ，当且仅当 a＝c 时，等号成立． 因此△ABC 面积的最大值为 2+1. 18． 解：(1)连结 AC1 交 A1C 于点 F，则 F 为 AC1 中点． 又 D 是 AB 中点，连结 DF，则 BC1∥DF. 因为 DF⊂平面 A1CD，BC1 平面 A1CD， 所以 BC1∥平面 A1CD. (2)由 AC＝CB＝ 2 2 AB 得，AC⊥BC. 以 C 为坐标原点，CA  的方向为 x 轴正方向，建立如图所示的空间直 角坐标系 C－xyz. 设 CA＝2，则 D(1,1,0)，E(0,2,1)，A1(2,0,2)，CD  ＝(1,1,0)，CE  ＝ (0,2,1)， 1CA  ＝(2,0,2)． 设 n＝(x1，y1，z1)是平面 A1CD 的法向量， 则 1 0, 0, CD CA        n n 即 1 1 1 1 0, 2 2 0. x y x z      可取 n＝(1，－1，－1)． 同理，设 m 是平面 A1CE 的法向量， 则 1 0, 0, CE CA        m m 可取 m＝(2,1，－2)． 从而 cos〈n，m〉＝ 3 | || | 3 ·n m n m ， 故 sin〈n，m〉＝ 6 3 . 即二面角 D－A1C－E 的正弦值为 6 3 . 19． 解：(1)当 X∈[100,130)时，T＝500X－300(130－X)＝800X－39 000， 当 X∈[130,150]时，T＝500×130＝65 000. 所以 800 39000,100 130, 65000,130 150. X XT X       (2)由(1)知利润 T 不少于 57 000 元当且仅当 120≤X≤150. 由直方图知需求量 X∈[120,150]的频率为 0.7，所以下一个销售季度 内的利润 T 不少于 57 000 元的概率的估计值为 0.7. (3)依题意可得 T 的分布列为 T 45 000 53 000 61 000 65 000 P 0.1 0.2 0.3 0.4 所以 ET＝45 000×0.1＋53 000×0.2＋61 000×0.3＋65 000×0.4 ＝59 400. 20． 解：(1)设 A(x1，y1)，B(x2，y2)，P(x0，y0)， 则 2 2 1 1 2 2 =1x y a b  ， 2 2 2 2 2 2 =1x y a b  ， 2 1 2 1 = 1y y x x   ， 由此可得 2 2 1 2 1 2 2 1 2 1 =1b x x y y a y y x x         . 因为 x1＋x2＝2x0，y1＋y2＝2y0， 0 0 1 2 y x  ， 所以 a2＝2b2. 又由题意知，M 的右焦点为( 3 ，0)，故 a2－b2＝3. 因此 a2＝6，b2＝3. 所以 M 的方程为 2 2 =16 3 x y . (2)由 2 2 3 0, 1,6 3 x y x y       解得 4 3 ,3 3 ,3 x y      或 0, 3. x y   因此|AB|＝ 4 6 3 . 由题意可设直线 CD 的方程为 y＝ 5 3 33x n n         ， 设 C(x3，y3)，D(x4，y4)． 由 2 2 , 16 3 y x n x y     得 3x2＋4nx＋2n2－6＝0. 于是 x3,4＝ 22 2 9 3 n n     . 因为直线 CD 的斜率为 1， 所以|CD|＝ 2 4 3 42 | | 93x x n   . 由已知，四边形 ACBD 的面积 21 8 6| | | | 92 9S CD AB n    . 当 n＝0 时，S 取得最大值，最大值为 8 6 3 . 所以四边形 ACBD 面积的最大值为 8 6 3 . 21． 解：(1)f′(x)＝ 1ex x m   . 由 x＝0 是 f(x)的极值点得 f′(0)＝0，所以 m＝1. 于是 f(x)＝ex－ln(x＋1)，定义域为(－1，＋∞)，f′(x)＝ 1e 1 x x   . 函数 f′(x)＝ 1e 1 x x   在(－1，＋∞)单调递增，且 f′(0)＝0. 因此当 x∈(－1,0)时，f′(x)＜0； 当 x∈(0，＋∞)时，f′(x)＞0. 所以 f(x)在(－1,0)单调递减，在(0，＋∞)单调递增． (2)当 m≤2，x∈(－m，＋∞)时，ln(x＋m)≤ln(x＋2)，故只需证明 当 m＝2 时，f(x)＞0. 当 m＝2 时，函数 f′(x)＝ 1e 2 x x   在(－2，＋∞)单调递增． 又 f′(－1)＜0，f′(0)＞0， 故 f′(x)＝0 在(－2，＋∞)有唯一实根 x0，且 x0∈(－1,0)． 当 x∈(－2，x0)时，f′(x)＜0； 当 x∈(x0，＋∞)时，f′(x)＞0，从而当 x＝x0 时，f(x)取得最小值． 由 f′(x0)＝0 得 0ex ＝ 0 1 2x  ，ln(x0＋2)＝－x0， 故 f(x)≥f(x0)＝ 0 1 2x  ＋x0＝ 2 0 0 1 2 x x     ＞0. 综上，当 m≤2 时，f(x)＞0. 请考生在第 22、23、24 题中任选择一题作答，如果多做，则按所做 的第一题计分，做答时请写清题号． 22． 解：(1)因为 CD 为△ABC 外接圆的切线， 所以∠DCB＝∠A，由题设知 BC DC FA EA  ， 故△CDB∽△AEF，所以∠DBC＝∠EFA. 因为 B，E，F，C 四点共圆， 所以∠CFE＝∠DBC， 故∠EFA＝∠CFE＝90°. 所以∠CBA＝90°，因此 CA 是△ABC 外接圆的直径． (2)连结 CE，因为∠CBE＝90°，所以过 B，E，F，C 四点的圆的直径 为 CE，由 DB＝BE，有 CE＝DC，又 BC2＝DB·BA＝2DB2，所以 CA2＝4DB2 ＋BC2＝6DB2. 而 DC2＝DB·DA＝3DB2，故过 B，E，F，C 四点的圆的面积与△ABC 外 接圆面积的比值为 1 2 . 23． 解：(1)依题意有 P(2cos α，2sin α)，Q(2cos 2α，2sin 2α)， 因此 M(cos α＋cos 2α，sin α＋sin 2α)． M 的轨迹的参数方程为 cos cos2 , sin sin 2 x y          (α为参数，0＜α＜2π)． (2)M 点到坐标原点的距离 2 2 2 2cosd x y     (0＜α＜2π)． 当α＝π时，d＝0，故 M 的轨迹过坐标原点． 24． 解：(1)由 a2＋b2≥2ab，b2＋c2≥2bc，c2＋a2≥2ca， 得 a2＋b2＋c2≥ab＋bc＋ca. 由题设得(a＋b＋c)2＝1，即 a2＋b2＋c2＋2ab＋2bc＋2ca＝1. 所以 3(ab＋bc＋ca)≤1，即 ab＋bc＋ca≤ 1 3 . (2)因为 2 2a b ab   ， 2 2b c bc   ， 2 2c a ca   ， 故 2 2 2 ( )a b c a b cb c a      ≥2(a＋b＋c)， 即 2 2 2a b c b c a   ≥a＋b＋c. 所以 2 2 2a b c b c a   ≥1. 2013 年普通高等学校数学文史类 (全国卷 I 新课标) 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符 合题目要求的． 1．(2013 课标全国Ⅰ，文 1)已知集合 A＝{1,2,3,4}，B＝{x|x＝n2，n∈A}，则 A∩B＝( )． A．{1,4} B．{2,3} C．{9,16} D．{1,2} 2．(2013 课标全国Ⅰ，文 2) 2 1 2i 1 i     ＝( )． A． 11 i2   B． 11+ i2  C． 11+ i2 D． 11 i2  3．(2013 课标全国Ⅰ，文 3)从 1,2,3,4 中任取 2 个不同的数，则取出的 2 个数之差的绝对 值为 2 的概率是( )． A． 1 2 B． 1 3 C． 1 4 D． 1 6 4．(2013 课标全国Ⅰ，文 4)已知双曲线 C： 2 2 2 2 =1x y a b  (a＞0，b＞0)的离心率为 5 2 ，则 C 的渐近线方程为( )． A．y＝ 1 4 x B．y＝ 1 3 x C．y＝ 1 2 x D．y＝±x 5．(2013 课标全国Ⅰ，文 5)已知命题 p：∀x∈R,2x＜3x；命题 q：∃x∈R，x3＝1－x2，则下 列命题中为真命题的是( )． A．p∧q B．  p∧q C．p∧  q D．  p∧  q 6．(2013 课标全国Ⅰ，文 6)设首项为 1，公比为 2 3 的等比数列{an}的前 n 项和为 Sn，则( )． A．Sn＝2an－1 B．Sn＝3an－2 C．Sn＝4－3an D．Sn＝3－ 2an 7．(2013 课标全国Ⅰ，文 7)执行下面的程序框图，如果输入的 t∈[－1,3]，则 输出的 s 属于( )． A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5] 8．(2013 课标全国Ⅰ，文 8)O 为坐标原点，F 为抛物线 C：y2＝ 4 2x 的焦点，P 为 C 上一点，若|PF|＝ 4 2 ，则△POF 的面积为( )． A．2 B． 2 2 C． 2 3 D．4 9．(2013 课标全国Ⅰ，文 9)函数 f(x)＝(1－cos x)sin x 在[－π，π]的图像大致为( )． 10．(2013 课标全国Ⅰ，文 10)已知锐角△ABC 的内角 A，B，C 的对边分别为 a，b，c,23cos2A ＋cos 2A＝0，a＝7，c＝6，则 b＝( )． A．10 B．9 C．8 D．5 11．(2013 课标全国Ⅰ，文 11)某几何体的三视图如图所示，则该几何体的体积为( )． A．16＋8π B．8＋8π C．16＋16π D．8＋16π 12．(2013 课标全国Ⅰ，文 12)已知函数 f(x)＝ 2 2 , 0, ln( 1), 0. x x x x x       若 |f(x)|≥ax，则 a 的取值范围是( )． A．(－∞，0] B．(－∞，1] C．[－2,1] D．[－2,0] 第Ⅱ卷 二、填空题：本大题共 4 小题，每小题 5 分． 13．(2013 课标全国Ⅰ，文 13)已知两个单位向量 a，b 的夹角为 60°，c＝ta＋(1－t)b.若 b·c＝0，则 t＝______. 14．(2013 课标全国Ⅰ，文 14)设 x，y 满足约束条件 1 3, 1 0, x x y       则 z＝2x－y 的最大值 为______． 15．(2013 课标全国Ⅰ，文 15)已知 H 是球 O 的直径 AB 上一点，AH∶HB＝1∶2，AB⊥平面α， H 为垂足，α截球 O 所得截面的面积为π，则球 O 的表面积为______． 16．(2013 课标全国Ⅰ，文 16)设当 x＝θ时，函数 f(x)＝sin x－2cos x 取得最大值，则 cos θ＝______. 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．(2013 课标全国Ⅰ，文 17)(本小题满分 12 分)已知等差数列{an}的前 n 项和 Sn 满足 S3＝0，S5＝－5. (1)求{an}的通项公式； (2)求数列 2 1 2 1 1 n na a        的前 n 项和． 18．(2013 课标全国Ⅰ，文 18)(本小题满分 12 分)为了比较两种治疗失眠症的药(分别称为 A 药，B 药)的疗效，随机地选取 20 位患者服用 A 药，20 位患者服用 B 药，这 40 位患者在 服用一段时间后，记录他们日平均增加的睡眠时间(单位：h)．试验的观测结果如下： 服用 A 药的 20 位患者日平均增加的睡眠时间： 0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4 服用 B 药的 20 位患者日平均增加的睡眠时间： 3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5 (1)分别计算两组数据的平均数，从计算结果看，哪种药的疗效更好？ (2)根据两组数据完成下面茎叶图，从茎叶图看，哪种药的疗效更好？ 19．(2013 课标全国Ⅰ，文 19)(本小题满分 12 分)如图，三棱柱 ABC－A1B1C1 中，CA＝CB， AB＝AA1，∠BAA1＝60°. (1)证明：AB⊥A1C； (2)若 AB＝CB＝2，A1C＝ 6 ，求三棱柱 ABC－A1B1C1 的体积． 20．(2013 课标全国Ⅰ，文 20)(本小题满分 12 分)已知函数 f(x)＝ex(ax ＋b)－x2－4x，曲线 y＝f(x)在点(0，f(0))处的切线方程为 y＝4x＋4. (1)求 a，b 的值； (2)讨论 f(x)的单调性，并求 f(x)的极大值． 21．(2013 课标全国Ⅰ，文 21)(本小题满分 12 分)已知圆 M：(x＋1)2＋y2＝1，圆 N：(x－1)2 ＋y2＝9，动圆 P 与圆 M 外切并且与圆 N 内切，圆心 P 的轨迹为曲线 C. (1)求 C 的方程； (2)l 是与圆 P，圆 M 都相切的一条直线，l 与曲线 C 交于 A，B 两点，当圆 P 的半径最长时， 求|AB|. 请考生在第(22)、(23)、(24)三题中任选一题做答．注意：只能做所选定的题目．如果多做， 则按所做的第一个题目计分，做答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑． 22．(2013 课标全国Ⅰ，文 22)(本小题满分 10 分)选修 4—1：几何证明选讲 如图，直线 AB 为圆的切线，切点为 B，点 C 在圆上，∠ABC 的角平分线 BE 交圆于点 E，DB 垂直 BE 交圆于点 D. 23．(2013 课标全国Ⅰ，文 23)(本小题满分 10 分)选修 4—4：坐标系与参数方程已知曲线 C1 的参数方程为 4 5cos , 5 5sin x t y t      (t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立 极坐标系，曲线 C2 的极坐标方程为ρ＝2sin θ. (1)把 C1 的参数方程化为极坐标方程； (2)求 C1 与 C2 交点的极坐标(ρ≥0,0≤θ＜2π)． 24．(2013 课标全国Ⅰ，文 24)(本小题满分 10 分)选修 4—5：不等式选讲已知函数 f(x)＝ |2x－1|＋|2x＋a|，g(x)＝x＋3. (1)当 a＝－2 时，求不等式 f(x)＜g(x)的解集； (2)设 a＞－1，且当 x∈ 1,2 2 a    时，f(x)≤g(x)，求 a 的取值范围． 2013 年普通高等学校数学文史类 (全国卷 I 新课标) 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符 合题目要求的． 1． 答案：A 解析：∵B＝{x|x＝n2，n∈A}＝{1,4,9,16}， ∴A∩B＝{1,4}． 2． 答案：B 解析： 2 1 2i 1 2i 1 2i i 2 i 1 i 2i 2 2             ＝ 11+ i2  . 3． 答案：B 解析：由题意知总事件数为 6，且分别为(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)，满 足条件的事件数是 2，所以所求的概率为 1 3 . 4． 答案：C 解析：∵ 5 2e  ，∴ 5 2 c a  ，即 2 2 5 4 c a  . ∵c2＝a2＋b2，∴ 2 2 1 4 b a  .∴ 1 2 b a  . ∵双曲线的渐近线方程为 by xa   ， ∴渐近线方程为 1 2y x  .故选 C. 5． 答案：B 解析：由 20＝30 知，p 为假命题．令 h(x)＝x3－1＋x2， ∵h(0)＝－1＜0，h(1)＝1＞0， ∴x3－1＋x2＝0 在(0,1)内有解． ∴∃x∈R，x3＝1－x2，即命题 q 为真命题．由此可知只有 p∧q 为真命题．故选 B. 6． 答案：D 解析： 11 211 3 21 1 1 3 n n n n aa a qa qS q q        ＝3－2an，故选 D. 7． 答案：A 解析：当－1≤t＜1 时，s＝3t，则 s∈[－3,3)． 当 1≤t≤3 时，s＝4t－t2. ∵该函数的对称轴为 t＝2， ∴该函数在[1,2]上单调递增，在[2,3]上单调递减． ∴smax＝4，smin＝3. ∴s∈[3,4]． 综上知 s∈[－3,4]．故选 A. 8． 答案：C 解析：利用|PF|＝ 2 4 2Px   ，可得 xP＝3 2 . ∴yP＝ 2 6 .∴S△POF＝ 1 2 |OF|·|yP|＝ 2 3 . 故选 C. 9． 答案：C 解析：由 f(x)＝(1－cos x)sin x 知其为奇函数．可排除 B．当 x∈ π0, 2      时，f(x)＞0， 排除 A. 当 x∈(0，π)时，f′(x)＝sin2x＋cos x(1－cos x)＝－2cos2x＋cos x＋1. 令 f′(x)＝0，得 2 π3x  . 故极值点为 2 π3x  ，可排除 D，故选 C. 10． 答案：D 解析：由 23cos2A＋cos 2A＝0，得 cos2A＝ 1 25 . ∵A∈ π0, 2      ，∴cos A＝ 1 5 . ∵cos A＝ 236 49 2 6 b b    ，∴b＝5 或 13 5b   (舍)． 故选 D. 11． 答案：A 解析：该几何体为一个半圆柱与一个长方体组成的一个组合体． V 半圆柱＝ 1 2 π×22×4＝8π， V 长方体＝4×2×2＝16. 所以所求体积为 16＋8π.故选 A. 12． 答案：D 解析：可画出|f(x)|的图象如图所示． 当 a＞0 时，y＝ax 与 y＝|f(x)|恒有公共点，所以排除 B，C； 当 a≤0 时，若 x＞0，则|f(x)|≥ax 恒成立． 若 x≤0，则以 y＝ax 与 y＝|－x2＋2x|相切为界限， 由 2 , 2 , y ax y x x     得 x2－(a＋2)x＝0. ∵Δ＝(a＋2)2＝0，∴a＝－2. ∴a∈[－2,0]．故选 D. 第Ⅱ卷 本卷包括必考题和选考题两部分．第 13 题～第 21 题为必考题，每个试题考生都必须做答．第 22 题～第 24 题为选考题，考生根据要求做答． 二、填空题：本大题共 4 小题，每小题 5 分． 13．答案：2 解析：∵b·c＝0，|a|＝|b|＝1，〈a，b〉＝60°，∴a·b＝ 1 11 1 2 2    . ∴b·c＝[ta＋(1－t)b]·b＝0， 即 ta·b＋(1－t)b2＝0. ∴ 1 2 t ＋1－t＝0. ∴t＝2. 14．答案：3 解析：画出可行域如图所示． 画出直线 2x－y＝0，并平移，当直线经过点 A(3,3)时，z 取最大 值，且最大值为 z＝2×3－3＝3. 15．答案： 9 π2 解析：如图， 设球 O 的半径为 R， 则 AH＝ 2 3 R ， OH＝ 3 R . 又∵π·EH2＝π，∴EH＝1. ∵在 Rt△OEH 中，R2＝ 2 2+13 R     ，∴R2＝ 9 8 . ∴S 球＝4πR2＝ 9π 2 . 16．答案： 2 5 5  解析：∵f(x)＝sin x－2cos x＝ 5 sin(x－φ)， 其中 sin φ＝ 2 5 5 ，cos φ＝ 5 5 . 当 x－φ＝2kπ＋ π 2 (k∈Z)时，f(x)取最大值． 即θ－φ＝2kπ＋ π 2 (k∈Z)，θ＝2kπ＋ π 2 ＋φ(k∈Z)． ∴cos θ＝ πcos 2     ＝－sin φ＝ 2 5 5  . 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17． 解：(1)设{an}的公差为 d，则 Sn＝ 1 ( 1) 2 n nna d . 由已知可得 1 1 3 3 0, 5 10 5, a d a d      解得 a1＝1，d＝－1. 故{an}的通项公式为 an＝2－n. (2)由(1)知 2 1 2 1 1 n na a  ＝ 1 1 1 1 3 2 1 2 2 2 3 2 1n n n n            ， 从而数列 2 1 2 1 1 n na a        的前 n 项和为 1 1 1 1 1 1 1 2 1 1 1 3 2 3 2 1n n            ＝ 1 2 n n . 18． 解：(1)设 A 药观测数据的平均数为 x ，B 药观测数据的平均数为 y . 由观测结果可得 x ＝ 1 20 (0.6＋1.2＋1.2＋1.5＋1.5＋1.8＋2.2＋2.3＋2.3＋2.4＋2.5＋2.6＋2.7＋2.7＋ 2.8＋2.9＋3.0＋3.1＋3.2＋3.5) ＝2.3， y ＝ 1 20 (0.5＋0.5＋0.6＋0.8＋0.9＋1.1＋1.2＋1.2＋1.3＋1.4＋1.6＋1.7＋1.8＋1.9＋ 2.1＋2.4＋2.5＋2.6＋2.7＋3.2) ＝1.6. 由以上计算结果可得 x ＞ y ，因此可看出 A 药的疗效更好． (2)由观测结果可绘制如下茎叶图： 从以上茎叶图可以看出，A 药疗效的试验结果有 7 10 的叶集中在茎 2,3 上，而 B 药疗效的试 验结果有 7 10 的叶集中在茎 0,1 上，由此可看出 A 药的疗效更好． 19． (1)证明：取 AB 的中点 O，连结 OC，OA1，A1B. 因为 CA＝CB， 所以 OC⊥AB. 由于 AB＝AA1，∠BAA1＝60°， 故△AA1B 为等边三角形， 所以 OA1⊥AB. 因为 OC∩OA1＝O，所以 AB⊥平面 OA1C. 又 A1C⊂平面 OA1C，故 AB⊥A1C. (2)解：由题设知△ABC 与△AA1B 都是边长为 2 的等边三角形， 所以 OC＝OA1＝ 3 . 又 A1C＝ 6 ，则 A1C2＝OC2＋ 2 1OA ， 故 OA1⊥OC. 因为 OC∩AB＝O，所以 OA1⊥平面 ABC，OA1 为三棱柱 ABC－A1B1C1 的高． 又△ABC 的面积 S△ABC＝ 3 ，故三棱柱 ABC－A1B1C1 的体积 V＝S△ABC×OA1＝3. 20． 解：(1)f′(x)＝ex(ax＋a＋b)－2x－4. 由已知得 f(0)＝4，f′(0)＝4. 故 b＝4，a＋b＝8. 从而 a＝4，b＝4. (2)由(1)知，f(x)＝4ex(x＋1)－x2－4x， f′(x)＝4ex(x＋2)－2x－4＝4(x＋2)· 1e 2 x    . 令 f′(x)＝0 得，x＝－ln 2 或 x＝－2. 从而当 x∈(－∞，－2)∪(－ln 2，＋∞)时，f′(x)＞0； 当 x∈(－2，－ln 2)时，f′(x)＜0. 故 f(x)在(－∞，－2)，(－ln 2，＋∞)上单调递增，在(－2，－ln 2)上单调递减． 当 x＝－2 时，函数 f(x)取得极大值，极大值为 f(－2)＝4(1－e－2)． 21． 解：由已知得圆 M 的圆心为 M(－1,0)，半径 r1＝1；圆 N 的圆心为 N(1,0)，半径 r2＝3.设圆 P 的圆心为 P(x，y)，半径为 R. (1)因为圆 P 与圆 M 外切并且与圆 N 内切， 所以|PM|＋|PN|＝(R＋r1)＋(r2－R)＝r1＋r2＝4. 由椭圆的定义可知，曲线 C 是以 M，N 为左、右焦点，长半轴长为 2，短半轴长为 3 的椭圆 (左顶点除外)，其方程为 2 2 =14 3 x y (x≠－2)． (2)对于曲线 C 上任意一点 P(x，y)，由于|PM|－|PN|＝2R－2≤2， 所以 R≤2，当且仅当圆 P 的圆心为(2,0)时，R＝2. 所以当圆 P 的半径最长时，其方程为(x－2)2＋y2＝4. 若 l 的倾斜角为 90°，则 l 与 y 轴重合，可得|AB|＝ 2 3 . 若 l 的倾斜角不为 90°，由 r1≠R 知 l 不平行于 x 轴，设 l 与 x 轴的交点为 Q，则 1 | | | | QP R QM r  ， 可求得 Q(－4,0)，所以可设 l：y＝k(x＋4)． 由 l 与圆 M 相切得 2 | 3 | 1 k k ＝1，解得 k＝ 2 4  . 当 k＝ 2 4 时，将 2 24y x  代入 2 2 =14 3 x y ，并整理得 7x2＋8x－8＝0，解得 x1,2＝ 4 6 2 7   ， 所以|AB|＝ 21 k |x2－x1|＝18 7 . 当 k＝ 2 4  时，由图形的对称性可知|AB|＝18 7 . 综上，|AB|＝ 2 3 或|AB|＝18 7 . 请考生在第(22)、(23)、(24)三题中任选一题做答．注意：只能做所选定的题目．如果多做， 则按所做的第一个题目计分，做答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑． 22． (1)证明：连结 DE，交 BC 于点 G. 由弦切角定理得，∠ABE＝∠BCE. 而∠ABE＝∠CBE， 故∠CBE＝∠BCE，BE＝CE. 又因为 DB⊥BE， 所以 DE 为直径，∠DCE＝90°， 由勾股定理可得 DB＝DC. (2)解：由(1)知，∠CDE＝∠BDE，DB＝DC， 故 DG 是 BC 的中垂线， 所以 BG＝ 3 2 . 设 DE 的中点为 O，连结 BO，则∠BOG＝60°. 从而∠ABE＝∠BCE＝∠CBE＝30°， 所以 CF⊥BF， 故 Rt△BCF 外接圆的半径等于 3 2 . 23． 解：(1)将 4 5cos , 5 5sin x t y t      消去参数 t，化为普通方程(x－4)2＋(y－5)2＝25， 即 C1：x2＋y2－8x－10y＋16＝0. 将 cos , sin x y        代入 x2＋y2－8x－10y＋16＝0 得ρ2－8ρcos θ－10ρsin θ＋16＝0. 所以 C1 的极坐标方程为 ρ2－8ρcos θ－10ρsin θ＋16＝0. (2)C2 的普通方程为 x2＋y2－2y＝0. 由 2 2 2 2 8 10 16 0, 2 0 x y x y x y y           解得 1, 1 x y    或 0, 2. x y    所以 C1 与 C2 交点的极坐标分别为 π2, 4      ， π2, 2      . 24． 解：(1)当 a＝－2 时，不等式 f(x)＜g(x)化为|2x－1|＋|2x－2|－x－3＜0. 设函数 y＝|2x－1|＋|2x－2|－x－3， 则 y＝ 15 , ,2 12, 1,2 3 6, 1. x x x x x x           其图像如图所示．从图像可知，当且仅当 x∈(0,2)时，y＜0. 所以原不等式的解集是{x|0＜x＜2}． (2)当 x∈ 1,2 2 a    时，f(x)＝1＋a. 不等式 f(x)≤g(x)化为 1＋a≤x＋3. 所以 x≥a－2 对 x∈ 1,2 2 a    都成立． 故 2 a ≥a－2，即 a≤ 4 3 . 从而 a 的取值范围是 41, 3     . 2012 年高考全国卷数学 1 试题及参考答案 数学（理科） 注意事项： 1. 答题前，考生务必将自己的姓名、准考证号填在试题卷和答题卡上，并将准考证号条形 码粘贴在答题卡上指定位置。 2. 选择题每小题选出答案后，用 2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其他答案标号，答在试题卷上无效。 3. 填空题和解答题用 0.5 毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内，答在 试题卷上无效。 4. 考试结束，请将本试题卷和答题卡一并上交。 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只 有一项是满足题目要求的。 1.复数 1z i  ， z 为 z 的共轭复数，则 1zz z  （） (A) -2i (B) -i (C) i (D) 2i 2. 函数  2 0y x x  的反函数为（） (A)   2 4 xy x R  (B)   2 04 xy x  (C)  24y x x R  (D)  24 0y x x  3.下面四个条件中，使 a b 成立的充分而不必要的条件是（） (A) 1a b  (B) 1a b  (C) 2 2a b (D) 3 3a b 4.设 nS 为等差数列 na 的前 n 项和，若 1 1a  ，公差 22, 24k kd S S   ，则 k=（） (A) 8 (B) 7 (C) 6 (D) 5 5.设函数    cos 0f x x   ，将  y f x 的图像向右平移 3  个单位长度后，所得的图 像与原图像重合，则 的最小值等于（） (A) 1 3 (B) 3 (C) 6 (D) 9 6.已知直二面角 l   ，点 , ,A AC l C  为垂足， , ,B BD l D  为垂足，若 2, 1AB AC BD   ，则 D 到平面 ABC 的距离等于（） (A) 2 2 (B) 3 3 (C) 6 3 (D) 1 7.某同学有同样的画册 2 本，同样的集邮册 3 本，从中取出 4 本赠送给 4 为朋友，每位朋友 1 本，则不同的赠送方法共有（） (A) 4 种 (B) 10 种 (C) 18 种 (D) 20 种 8.曲线 2 1xy e  在点 0,2 处的切线与直线 0y  和 y x 围成的三角形的面积为（） (A) 1 3 (B) 1 2 (C) 2 3 (D) 1 9.设  f x 是周期为 2 的奇函数，当 0 1x  时，    2 1f x x x  ，则 5 2f      （） (A) 1 2  (B) 1 4  (C) 1 4 (D) 1 2 10.已知抛物线 C： 2 4y x 的焦点为 F，直线 2 4y x  与 C 交于 A、B 两点，则 cos AFB  （） (A) 4 5 (B) 3 5 (C) 3 5  (D) 4 5  11.已知平面 截一球面得圆 M，过圆心 M 且与 成 60 二面角的平面  截该球面得圆 N，若 该球面的半径为 4.圆 M 的面积为 4 ，则圆 N 的面积为（） (A) 7 (B) 9 (C) 11 (D) 13 12. 设向量 , ,a b c    满足 11, , , 602a b a b a c b c                ，则 c  的最大值等于（） (A) 2 (B) 3 (C) 2 (D) 1 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分.请将答案填在答题卡对应题号的位 置上,一题两空的题,其答案按先后次序填写. 13.  20 1 x 的二项展开式中， x 的系数与 9x 的系数之差为 . 14. 已知 ,2      ， 5sin 5   ，则 tan 2  . 15. 已知 1 2F F、 分别为双曲线 2 2 : 19 27 x yC   的左、右焦点，点 A C ，点 M 的坐标为 2,0 ， AM 为 1 2F AF 的角平分线，则 2AF  . 16. 已知点 E、F 分别在正方体 1 1 1 1ABCD A B C D 的棱 1 1BB CC、 上，且 1 2B E EB , 12CF FC ,则面 AEF 与面 ABC 所成的二面角的正切值等于 . 三、解答题：本大题共 6 小题，共 70 分。解答应写出文字说明、证明过程或演算步骤。 17.（本小题满分 10 分） ABC 的内角 A、B、C 的对边分别为 , ,a b c 。已知 90 , 2A C a c b    ，求 C 18.（本小题满分 12 分） 根据以往统计资料，某地车主购买甲种保险的概率为 0.5，购买乙种保险但不购买甲种 保险的概率为 0.3，设各车主购买保险相互独立。 （Ⅰ）求该地 1 为车主至少购买甲、乙两种保险中的 1 种的概率； （Ⅱ）X 表示该地的 100 为车主中，甲、乙两种保险都不购买的车主数，求 X 的期望。 19.（本小题满分 12 分） 如图，四棱锥 S-ABCD 中， / / ,AB CD BC CD ,侧面 SAB 为 等边三角形， AB=BC=2，CD=SD=1. （Ⅰ）证明： SD SAB 平面 ; （Ⅱ）求 AB 与平面 SBC 所成的角的大小。 20.（本小题满分 12 分） 设数列 na 满足 1 1 1 10, 11 1n n a a a     （Ⅰ）求 na 的通项公式； （Ⅱ）设 11 n n ab n  ，记 1 n n k k S b    ，证明： 1nS  。 21.（本小题满分 12 分） 已知O 为坐标原点，F为椭圆 2 2: 12 yC x   在 y轴正半轴上的焦点，过 F且斜率为 2 的 直 线 l 与 C 交 于 A 、 B 两 点 ， 点 P 满 足 0.OA OB OP     （Ⅰ）证明：点 P 在 C 上； （Ⅱ）设点 P 关于点 O 的对称点为 Q，证明：A、P、B、Q 四点在同一个圆上。 22.（本小题满分 12 分） （Ⅰ）设函数     2ln 1 2 xf x x x     ，证明：当 0x  时，   0f x  （Ⅱ）从编号 1 到 100 的 100 张卡片中每次随机抽取一张，然后放回，用这种方式连续 抽取 20 次，设抽到的 20 个号码互不相同的概率为 p ，证明： 19 2 9 1 10p e      2011 年普通高等学校招生全国统一考试（全国卷） 数学试题参考答案 仅供参考 一、选择题：本题考查基础知识和基本运算．每小题 5 分，满分 60 分． 1． B 2． B 3． A 4． D 5．C 6． C 7． B 8． D 9． A 10 ． D 11. D 12. A 二、填空题：本题考查基础知识和基本运算．每小题 5 分，满分 20 分． 13． 0 14． 4 3  15．6 16． 2 3 三、解答题：本大题共 6 小题，共 70 分． 17.（本小题满分 10 分） 解：由 90A C   ，得 22B A C C     故sin sin cos2A C C      ，sin sin 2 cos22B C C      由 2 sin sin 2 sina c b A C B     ， 故 cos sin 2 cos2C C C  ，  2 2cos sin 2 cos sinC C C C   又显然 2C  ，故 2cos sin 2C C  ，再由 2 2cos sin 1C C  ， 解得： 6 2cos 4C  ，于是 12C  18.（本小题满分 12 分） 解：（Ⅰ）设购买乙种保险的概率为 x ,因为购买乙种保险但不购买甲种保险的概率为 0.3 故 1 0.5 0.3 0.6x x    ， 所以该地 1 为车主至少购买甲、乙两种保险中的 1 种的概率为   1 1 0.5 1 0.6 0.8    （Ⅱ）由（Ⅰ）易知，甲、乙两种保险都不购买的概率为1 0.8 0.2  所以有 X 个车主甲、乙两种保险都不购买的概率为    100 100 0.2 0.8X XXp C   显然，X 服从二项分布，即  100,0.2X B ,所以 100 0.2 20EX    X 的期望为 20 19.（本小题满分 12 分） （Ⅰ）证明：在直角梯形 ABCD 中，AB=BC=2，CD=1， / / ,AB CD BC CD ， 易算得： 5AD BD  ， 又因为侧面 SAB 为等边三角形，SD=1，AB=2， 所以 2 2 25SD SA AD   , 2 2 25SD SB BD   于是 SD SA , SD SB ,所以 SD SAB 平面 （Ⅱ）设点 A 到平面 SBC 的距离为 d， 因为 SD SAB 平面 ，所以 SD AB ,从而 SD CD , 因而可以算得： 2SC  ，又 2SB BC  ，故 7 2SBCS  又因为 / /CD SAB平面 ,所以点 C 到平面 SAB 的距离为 1SD  另外，显然 23 2 34SBAS    ，所以 1 7 1 3 13 2 3A SBC C SABV d V      四棱锥 四棱锥 得： 2 21 7d  设 AB 与平面 SBC 所成的角为 ，则 2 21 217sin 2 7    ， 即 AB 与平面 SBC 所成的角为 21sin 7arc （显然 是锐角） 20.（本小题满分 12 分） 解：（Ⅰ）由 1 1 1 11 1n na a    得：数列 1 1 na      是等差数列，首项为 1 1 11 a  故  1 1 1 11 n n na      ，从而 11na n   （Ⅱ） 1 11 11 1 1 11 1 1 n n a n nnb n n n n n n            所以 1 1 1 1 1 1 11 1 1 2 2 3 1 1 n n k k S b n n n               21.（本小题满分 12 分） （Ⅰ）证明：易知：  0,1F ，故： : 2 1l y x   ，代入椭圆方程得： 24 2 2 1 0x x   ， 设      1 1 2 2, , , , ,A x y B x y P x y ，则 1 2 2 2x x  ，  1 2 1 22 2 1y y x x      ， 因为 0.OA OB OP     所以       1 1 2 2, , , 0,0x y x y x y      1 2 1 2 2, , , 12x y x x y y             ，将此坐标代入椭圆： 2 22 1 12 2        ， 所以点 P 在 C 上。 （ Ⅱ ） 由 （ Ⅰ ） ： 24 2 2 1 0x x   及 : 2 1l y x   ， 得 2 6 3 1 2 6 1 3, , ,4 2 4 2A B                 ，因为 2 , 12p       ，所以 2 ,12Q       于是可以算得： 2 2 6APk   ， 6 2 2AQk   ， 2 2 6BPk   ， 6 2 2BQk    tan 4 2PBQ   , 2tan 63APB  , tan 4 2PAQ   2tan 63AQB  于是四边形 APBQ 对角互补，从而 A、P、B、Q 四点在同一个圆上。 22 .（本小题满分 12 分） 证明：（Ⅰ） 0x  时，          2 2 2 2 2 21 01 2 1 2 x x xf x x x x x          ， 于是  f x 在 0, 上单调增，所以    0 0f x f  （Ⅱ） 20 19 100 99 82 81 99 98 81 100 100p              19 99 81 (98 81) 91 89 90 100         （共有19 1 92   对数相乘） 192 2 2 19 19 19 90 90 90 90 90 90 100 100 10x              由（Ⅰ）， 1 0x   时，也有      2 2 0 1 2 xf x x x      ， 故  f x 在 1,0 上单调增，所以  1 0 010f f      即 1 1 9 9 25ln ln 01910 10 10 19 10 f                      即 919ln 210       ，两边同时取 e 的对数得： 19 2 2 9 1 10 e e       综上所述： 19 2 9 1 10p e      2011 年普通高等学校招生全国统一考试(全国卷) 数学 本试卷共 4 页，三大题 21 小题。满分 150 分，考试时间 120 分钟。 注意事项： 1. 答题前，考生务必将自己的姓名、准考证号填在试题卷和答题卡上，并将准考证号条形 码粘贴在答题卡上指定位置。 2. 选择题每小题选出答案后，用 2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其他答案标号，答在试题卷上无效。 3. 填空题和解答题用 0.5 毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内，答在 试题卷上无效。 4. 考试结束，请将本试题卷和答题卡一并上交。 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只 有一项是满足题目要求的。 1.复数 1z i  ， z 为 z 的共轭复数，则 1zz z   (A) -2i (B) -i (C) i (D) 2i 2. 函数  2 0y x x  的反函数为 (A)   2 4 xy x R  (B)   2 04 xy x  (C)  24y x x R  (D)  24 0y x x  3.下面四个条件中，使 a b 成立的充分而不必要的条件是 (A) 1a b  (B) 1a b  (C) 2 2a b (D) 3 3a b 4.设 nS 为等差数列 na 的前 n 项和，若 1 1a  ，公差 22, 24k kd S S   ，则 k= (A) 8 (B) 7 (C) 6 (D) 5 5.设函数    cos 0f x x   ，将  y f x 的图像向右平移 3  个单位长度后，所得的图 像与原图像重合，则 的最小值等于 (A) 1 3 (B) 3 (C) 6 (D) 9 6.已知直二面角 l   ，点 , ,A AC l C  为垂足， , ,B BD l D  为垂足，若 2, 1AB AC BD   ，则 D 到平面 ABC 的距离等于 (A) 2 2 (B) 3 3 (C) 6 3 (D) 1 7.某同学有同样的画册 2 本，同样的集邮册 3 本，从中取出 4 本赠送给 4 为朋友，每位朋友 1 本，则不同的赠送方法共有 (A) 4 种 (B) 10 种 (C) 18 种 (D) 20 种 8.曲线 2 1xy e  在点 0,2 处的切线与直线 0y  和 y x 围成的三角形的面积为 (A) 1 3 (B) 1 2 (C) 2 3 (D) 1 9.设  f x 是周期为 2 的奇函数，当 0 1x  时，    2 1f x x x  ，则 5 2f      (A) 1 2  (B) 1 4  (C) 1 4 (D) 1 2 10.已知抛物线 C： 2 4y x 的焦点为 F，直线 2 4y x  与 C 交于 A、B 两点，则 cos AFB  (A) 4 5 (B) 3 5 (C) 3 5  (D) 4 5  11.已知平面 截一球面得圆 M，过圆心 M 且与 成 60 二面角的平面  截该球面得圆 N，若 该球面的半径为 4.圆 M 的面积为 4 ，则圆 N 的面积为 (A) 7 (B) 9 (C) 11 (D) 13 12. 设向量 , ,a b c    满足 11, , , 602a b a b a c b c                ，则 c  的最大值等于 (A) 2 (B) 3 (C) 2 (D) 1 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分.请将答案填在答题卡对应题号的位 置上,一题两空的题,其答案按先后次序填写. 13.  20 1 x 的二项展开式中， x 的系数与 9x 的系数之差为 . 14. 已知 ,2      ， 5sin 5   ，则 tan 2  . 15. 已知 1 2F F、 分别为双曲线 2 2 : 19 27 x yC   的左、右焦点，点 A C ，点 M 的坐标为 2,0 ， AM 为 1 2F AF 的角平分线，则 2AF  . 16. 已知点 E、F 分别在正方体 1 1 1 1ABCD A B C D 的棱 1 1BB CC、 上，且 1 2B E EB , 12CF FC ,则面 AEF 与面 ABC 所成的二面角的正切值等于 . 三、解答题：本大题共 6 小题，共 70 分。解答应写出文字说明、证明过程或演算步骤。 17.（本小题满分 10 分） ABC 的内角 A、B、C 的对边分别为 , ,a b c 。已知 90 , 2A C a c b    ，求 C 18.（本小题满分 12 分） 根据以往统计资料，某地车主购买甲种保险的概率为 0.5，购买乙种保险但不购买甲种 保险的概率为 0.3，设各车主购买保险相互独立。 （Ⅰ）求该地 1 为车主至少购买甲、乙两种保险中的 1 种的概率； （Ⅱ）X 表示该地的 100 为车主中，甲、乙两种保险都不购买的车主数，求 X 的期望。 19.（本小题满分 12 分） 如图，四棱锥 S-ABCD 中， / / ,AB CD BC CD ,侧面 SAB 为等边三角形， AB=BC=2，CD=SD=1. （Ⅰ）证明： SD SAB 平面 ; （Ⅱ）求 AB 与平面 SBC 所成的角的大小。 20.（本小题满分 12 分） 设数列 na 满足 1 1 1 10, 11 1n n a a a     （Ⅰ）求 na 的通项公式； （Ⅱ）设 11 n n ab n  ，记 1 n n k k S b    ，证明： 1nS  。 21.（本小题满分 12 分） 已知 O 为坐标原点，F 为椭圆 2 2: 12 yC x   在 y 轴正半轴上的焦点，过 F 且斜率为 2 的直线l 与 C 交于 A、B 两点，点 P 满足 0.OA OB OP     （Ⅰ）证明：点 P 在 C 上； （Ⅱ）设点 P 关于点 O 的对称点为 Q，证明：A、P、B、Q 四点在同一个圆上。 22.（本小题满分 12 分） （Ⅰ）设函数     2ln 1 2 xf x x x     ，证明：当 0x  时，   0f x  （Ⅱ）从编号 1 到 100 的 100 张卡片中每次随机抽取一张，然后放回，用这种方式连续 抽取 20 次，设抽到的 20 个号码互不相同的概率为 p ，证明： 19 2 9 1 10p e      2011 年普通高等学校招生全国统一考试（全国卷） 数学试题参考答案（不是标准答案） 一、选择题：本题考查基础知识和基本运算．每小题 5 分，满分 60 分． 1． B 2． B 3． A 4． D 5．C 6． C 7． B 8． D 9． A 10．D 11. D 12. A 二、填空题：本题考查基础知识和基本运算．每小题 5 分，满分 20 分． 13． 0 14． 4 3  15．6 16． 2 3 三、解答题：本大题共 6 小题，共 70 分． 17.（本小题满分 10 分） 解：由 90A C   ，得 22B A C C     故sin sin cos2A C C      ，sin sin 2 cos22B C C      由 2 sin sin 2 sina c b A C B     ， 故 cos sin 2 cos2C C C  ，  2 2cos sin 2 cos sinC C C C   又显然 2C  ，故 2cos sin 2C C  ，再由 2 2cos sin 1C C  ， 解得： 6 2cos 4C  ，于是 12C  18.（本小题满分 12 分） 解：（Ⅰ）设购买乙种保险的概率为 x ,因为购买乙种保险但不购买甲种保险的概率为 0.3 故 1 0.5 0.3 0.6x x    ， 所以该地 1 为车主至少购买甲、乙两种保险中的 1 种的概率为   1 1 0.5 1 0.6 0.8    （Ⅱ）由（Ⅰ）易知，甲、乙两种保险都不购买的概率为1 0.8 0.2  所以有 X 个车主甲、乙两种保险都不购买的概率为    100 100 0.2 0.8X XXp C   显然，X 服从二项分布，即  100,0.2X B , 所以 100 0.2 20EX    X 的期望为 20 19.（本小题满分 12 分） （Ⅰ）证明：在直角梯形 ABCD 中，AB=BC=2，CD=1， / / ,AB CD BC CD ， 易算得： 5AD BD  ， 又因为侧面 SAB 为等边三角形，SD=1，AB=2， 所以 2 2 25SD SA AD   , 2 2 25SD SB BD   于是 SD SA , SD SB , 所以 SD SAB 平面 （Ⅱ）设点 A 到平面 SBC 的距离为 d， 因为 SD SAB 平面 ，所以 SD AB ,从而 SD CD , 因而可以算得： 2SC  ，又 2SB BC  ，故 7 2SBCS  又因为 / /CD SAB平面 ,所以点 C 到平面 SAB 的距离为 1SD  另外，显然 23 2 34SBAS    ， 所以 1 7 1 3 13 2 3A SBC C SABV d V      四棱锥 四棱锥 得： 2 21 7d  设 AB 与平面 SBC 所成的角为 ，则 2 21 217sin 2 7    ， 即 AB 与平面 SBC 所成的角为 21sin 7arc （显然 是锐角） 20.（本小题满分 12 分） 解：（Ⅰ）由 1 1 1 11 1n na a    得： 数列 1 1 na      是等差数列，首项为 1 1 11 a  故  1 1 1 11 n n na      ，从而 11na n   （Ⅱ） 1 11 11 1 1 11 1 1 n n a n nnb n n n n n n            所以 1 1 1 1 1 1 11 1 1 2 2 3 1 1 n n k k S b n n n               21.（本小题满分 12 分） （Ⅰ）证明：易知：  0,1F ，故： : 2 1l y x   ，代入椭圆方程得： 24 2 2 1 0x x   ， 设      1 1 2 2, , , , ,A x y B x y P x y ，则 1 2 2 2x x  ，  1 2 1 22 2 1y y x x      ， 因为 0.OA OB OP     所以       1 1 2 2, , , 0,0x y x y x y      1 2 1 2 2, , , 12x y x x y y             ，将此坐标代入椭圆： 2 22 1 12 2        ， 所以点 P 在 C 上。 （ Ⅱ ） 由 （ Ⅰ ） ： 24 2 2 1 0x x   及 : 2 1l y x   ， 得 2 6 3 1 2 6 1 3, , ,4 2 4 2A B                 ，因为 2 , 12p       ，所以 2 ,12Q       于是可以算得： 2 2 6APk   ， 6 2 2AQk   ， 2 2 6BPk   ， 6 2 2BQk    tan 4 2PBQ   , 2tan 63APB  , tan 4 2PAQ   2tan 63AQB  于是四边形 APBQ 对角互补，从而 A、P、B、Q 四点在同一个圆上。 22 .（本小题满分 12 分） 证明：（Ⅰ） 0x  时，          2 2 2 2 2 21 01 2 1 2 x x xf x x x x x          ， 于是  f x 在 0, 上单调增，所以    0 0f x f  （Ⅱ） 20 19 100 99 82 81 99 98 81 100 100p              19 99 81 (98 81) 91 89 90 100         （共有19 1 92   对数相乘） 192 2 2 19 19 19 90 90 90 90 90 90 100 100 10x              由（Ⅰ）， 1 0x   时，也有      2 2 0 1 2 xf x x x      ， 故  f x 在 1,0 上单调增，所以  1 0 010f f      即 1 1 9 9 25ln ln 01910 10 10 19 10 f                      即 919ln 210       ，两边同时取 e 的对数得： 19 2 2 9 1 10 e e       综上所述： 19 2 9 1 10p e      2010 年普通高等学校招生全国统一考试 理科数学(必修+选修 II) 本试卷分第 I 卷(选择题)和第Ⅱ卷(非选择题)两部分。第 I 卷 1 至 2 页。第Ⅱ卷 3 至 4 页。考试结束后，将本试卷和答题卡一并交回。 第 I 卷 注意事项： 1．答题前，考生在答题卡上务必用直径 0.5 毫米黑色墨水签字笔将自己的姓名、 准考证号填写清楚，并贴好条形码。请认真核准条形码上的准考证号、姓名和科目。 2．每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效．．．．．．．．．。 3．第 I 卷共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。参考公式： 如果事件 A、B 互斥，那么 球的表面积公式 ( ) ( ) ( )P A B P A P B   24S R 如果事件 A、B 相互独立，那么 其中 R 表示球的半径 ( ) ( ) ( )P A B P A P B  球的体积公式 如果事件 A 在一次试验中发生的概率是 p ，那么 33 4V R n 次独立重复试验中事件 A 恰好发生 k 次的概率 其中 R 表示球的半径 ( ) (1 ) ( 0,1,2, )k k n k n nP k C p p k n   … 一．选择题 (1)复数 3 2 2 3 i i   (A)i (B) i (C)12-13i (D) 12+13i 1．A【命题意图】本小题主要考查复数的基本运算,重点考查分母实数化的转化技巧. 【解析】 3 2 (3 2 )(2 3 ) 6 9 4 6 2 3 (2 3 )(2 3 ) 13 i i i i i ii i i           . (2)记 cos( 80 ) k   ,那么 tan100  A. 21 k k  B. - 21 k k  C. 21 k k D. - 21 k k 2.B 【命题意图】本小题主要考查诱导公式、同角三角函数关系式等三角函数知识，并突 出了弦切互化这一转化思想的应用. 【解析】 2 2 2sin80 1 cos 80 1 cos ( 80 ) 1 k         ,所以 tan100 tan80    2sin80 1 .cos80 k k       (3)若变量 ,x y 满足约束条件 1, 0, 2 0, y x y x y         则 2z x y  的最大值为 (A)4 (B)3 (C)2 (D)1 3.B 【命题意图】本小题主要考查线性规划知识、作图、识图能力及计算能力. 【解析】画出可行域（如右图），由图可知,当直线l 经过点 A(1,-1)时，z 最大，且最 大值为 max 1 2 ( 1) 3z      . （4）已知各项均为正数的等比数列{ na }， 1 2 3a a a =5， 7 8 9a a a =10，则 4 5 6a a a = (A) 5 2 (B) 7 (C) 6 (D) 4 2 4.A【命题意图】本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等 知识，着重考查了转化与化归的数学思想. 【 解 析 】 由 等 比 数 列 的 性 质 知 3 1 2 3 1 3 2 2( ) 5a a a a a a a   ， 3 7 8 9 7 9 8 8( )a a a a a a a   10,所以 1 3 2 8 50a a  , 所以 1 3 3 36 4 5 6 4 6 5 5 2 8( ) ( ) (50 ) 5 2a a a a a a a a a     (5) 3 53(1 2 ) (1 )x x  的展开式中 x 的系数是 (A) -4 (B) -2 (C) 2 (D) 4 5.B 【命题意图】本小题主要考查了考生对二项式定理的掌握情况，尤其是 展开式的通项公式的灵活应用，以及能否区分展开式中项的系数与其二项 式系数，同时也考查了考生的一些基本运算能力. 【解析】 3 5 53 3(1 2 ) (1 ) (1 6 12 8 )(1 )x x x x x x x       0x y  1 O y x y 2 0x y   x A 0 : 2 0l x y  2 2 A A B CD A1 B1 C1 D1 O 故 3 53(1 2 ) (1 )x x  的 展 开 式 中 含 x 的 项 为 3 3 03 5 51 ( ) 12 10 12 2C x xC x x x        ,所以 x 的系数为-2. (6)某校开设 A 类选修课 3 门，B 类选择课 4 门，一位同学从中共选 3 门， 若要求两类课程中各至少选一 门，则不同的选法共有 (A) 30 种 (B)35 种 (C)42 种 (D)48 种 6.A【命题意图】本小题主要考查分类计数原理、组合知识,以及分类讨论的 数学思想. 【解析】:可分以下 2 种情况:(1)A 类选修课选 1 门,B 类选修课选 2门,有 1 2 3 4C C 种不同的选法;(2)A 类选修课选 2 门,B 类选修课选 1 门,有 2 1 3 4C C 种不同的 选法.所以不同的选法共有 1 2 3 4C C + 2 1 3 4 18 12 30C C    种. (7)正方体 ABCD- 1 1 1 1A B C D 中，B 1B 与平面 AC 1D 所成角的余弦值为 A 2 3 B 3 3 C 2 3 D 6 3 7.D 【命题意图】本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的 求法，利用等体积转化求出 D 到平面 AC 1D 的距离是解决本题的关键所在,这也是转化思想 的具体体现. 【解析】因为 BB1//DD1,所以 B 1B 与平面 AC 1D 所成角和 DD1 与 平面 AC 1D 所成角相等,设 DO⊥平面 AC 1D ，由等体积法得 1 1D ACD D ACDV V  ,即 1 1 1 1 3 3ACD ACDS DO S DD    .设 DD1=a, 则 1 2 2 1 1 1 3 3sin 60 ( 2 )2 2 2 2ACDS AC AD a a      , 21 1 2 2ACDS AD CD a   . 所 以 1 3 1 2 3 33 ACD ACD S DD aDO aS a      , 记 DD1 与 平 面 AC 1D 所 成 角 为  , 则 1 3sin 3 DO DD    ,所以 6cos 3   . （8）设 a= 3log 2,b=In2,c= 1 25  ,则 A af(1)=1+ 2 1 =3,即 a+2b 的取值范围是(3,+∞). （11）已知圆 O 的半径为 1，PA、PB 为该圆的两条切线，A、B 为俩切点，那么 PA PB  的 最小值为 (A) 4 2  (B) 3 2  (C) 4 2 2  (D) 3 2 2  11.D【命题意图】本小题主要考查向量的数量积运算与圆的切线长定理，着重考查最值的求 法——判别式法,同时也考查了考生综合运用数学 知识解题的能力及运算能力. 【解析】如图所示：设 PA=PB= x ( 0)x  ,∠APO= 则∠APB= 2 ，PO= 21 x ， 2 1sin 1 x    ， | | | | cos2PA PB PA PB       = 2 2(1 2sin )x  = 2 2 2 ( 1) 1 x x x   = 4 2 2 1 x x x   ，令 PA PB y   ，则 4 2 2 1 x xy x   ，即 4 2(1 ) 0x y x y    ，由 2x 是实数，所以 2[ (1 )] 4 1 ( ) 0y y         ， 2 6 1 0y y   ，解得 3 2 2y    或 3 2 2y    . 故 min( ) 3 2 2PA PB     .此时 2 1x   . （12）已知在半径为 2 的球面上有 A、B、C、D 四点，若 AB=CD=2,则四面体 ABCD 的体 积的最大值为 (A) 2 3 3 (B) 4 3 3 (C) 2 3 (D) 8 3 3 12.B【命题意图】本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过 球这个载体考查考生的空间想象能力及推理运算能力. 【解析】过 CD 作平面 PCD，使 AB⊥平面 PCD,交 AB 与 P,设点 P 到 CD 的距离为 h ,则有 ABCD 1 1 22 23 2 3V h h     四面体 ,当直径通过 AB 与 CD 的中点时, 2 2 max 2 2 1 2 3h    ,故 max 4 3 3V  . P A B O 绝密★启用前 2010 年普通高等学校招生全国统一考试 理科数学(必修+选修 II) 第Ⅱ卷 注意事项： 1．答题前，考生先在答题卡上用直径 0.5 毫米黑色墨水签字笔将自己的姓名、准考 证号填写清楚，然后贴好条形码。请 认真核准条形码上的准考证号、姓名和科目。 2．第Ⅱ卷共 2 页，请用直径 0.5 毫米黑色墨水签字笔在答题卡上各题的答题区域 内作答，在试题卷上作答无效．．．．．．．．．。 3。第Ⅱ卷共 l0 小题，共 90 分。 二．填空题：本大题共 4 小题，每小题 5 分，共 20 分．把答案填在题中横线上． (注意：在试题卷上作答无效) (13)不等式 22 1 1x x   的解集是 . 13.[0,2] 【命题意图】本小题主要考查根式不等式的解法，利用平方去掉根号是解根式不 等式的基本思路，也让转化与化归的数学思想体现得淋漓尽致. 解析:原不等式等价于 2 22 1 ( 1) , 1 0 x x x        解得 0≤x≤2. (14)已知 为第三象限的角， 3cos2 5    ,则 tan( 2 )4    . 14． 1 7  【命题意图】本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的 正切公式,同时考查了基本运算能力及等价变换的解题技能. 【解析】因为  为第三象限的角,所以 2 (2(2 1) , 2(2 1) )( )k k k Z        ，又 3cos2 5    <0, 所以 2 ( 2(2 1) , 2(2 1) )( )2 k k k Z         ,于是有 4sin 2 5   , sin 2 4tan 2 cos2 3     ,所以 tan( 2 )4    41tan tan 2 134 4 71 tan tan 2 14 3           . (15)直线 1y  与曲线 2y x x a   有四个交点，则 a 的取值范围是 . 15.(1, 5)4 【命题意图】本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形 结合的数学思想. 1 2x  y=1 x y a O 1 2x   4 1 4 ay  2y x x a   【解析】如图，在同一直角坐标系内画出直线 1y  与曲线 2y x x a   ,观图可知，a 的 取值必须满足 1 ,4 1 14 a a    解得 51 4a  . (16)已知 F 是椭圆 C 的一个焦点， B 是短轴的一个端点，线段 BF 的 延 长 线 交 C 于 点 D ， 且 BF 2FD uur uur ， 则 C 的 离 心 率 为 . 16. 2 3 【命题意图】本小题主要考查椭圆的方程与几何性质、第二 定义、平面向量知识，考查了数形结合思想、方程思想,本 题凸显解析几何的特点：“数研究形，形助数”，利用几何性 质可寻求到简化问题的捷径. 【解析】如图， 2 2| |BF b c a   , 作 1DD y 轴于点 D1,则由 BF 2FD uur uur ，得 1 | | | | 2 | | | | 3 OF BF DD BD   ,所以 1 3 3| | | |2 2DD OF c  , 即 3 2D cx  ,由椭圆的第二定义得 2 23 3| | ( )2 2 a c cFD e ac a     又由| | 2 | |BF FD ,得 232 cc a a   ,整理得 2 23 2 0c a ac   . 两边都除以 2a ,得 23 2 0e e   ,解得 1( )e   舍去 ，或 2 3e  . 三．解答题：本大题共 6 小题，共 70 分．解答应写出文字说明，证明过程或演算步 骤． (17)(本小题满分 10 分)(注意：在试题卷上作答无效．．．．．．．．．．．．) 已知 ABCV 的内角 A ， B 及其对边 a ，b 满足 cot cota b a A b B   ，求内角 C ． 17. 【命题意图】本小题主要考查三角恒等变形、利用正弦、余弦定理处理三角形中的 边角关系，突出考查边角互化的转化思想的应用. (18)(本小题满分 12 分)（注意：在试题卷上作答无效．．．．．．．．．)． 投到某杂志的稿件，先由两位初审专家进行评审．若能通过两位初审专家的评审， 则予以录用；若两位初审专家都未予通过，则不予录用；若恰能通过一位初审专家的评 审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则不予录 用．设稿件能通过各初审专家评审的概率均为0．5，复审的稿件能通过评审的概率为0．3． 各专家独立评审． xO y B F 1D D (I)求投到该杂志的 1 篇稿件被录用的概率； (II)记 X 表示投到该杂志的 4 篇稿件中被录用的篇数，求 X 的分布列及期望． 18. 【命题意图】本题主要考查等可能性事件、互斥事件、独立事件、相互独立试验、 分布列、数学期望等知识,以及运用概率知识解决实际问题的能力,考查分类与整合思 想、化归与转化思想. （19）（本小题满分 12 分）（注意：在试题卷上作答无效．．．．．．．．．） 如图，四棱锥 S-ABCD 中，SD  底面 ABCD，AB//DC，AD  DC，AB=AD=1，DC=SD=2， E 为棱 SB 上的一点，平面 EDC  平面 SBC . （Ⅰ）证明：SE=2EB； （Ⅱ）求二面角 A-DE-C 的大小 . 【命题意图】本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系，二面 角等基础知识,考查空间想象能力、推理论证能力和运算能力. (20)(本小题满分 12 分)（注意：在试题卷上作答无效．．．．．．．．．） 已知函数 ( ) ( 1)ln 1f x x x x    . （Ⅰ）若 2'( ) 1xf x x ax   ，求 a 的取值范围； （Ⅱ）证明： ( 1) ( ) 0x f x  . 【命题意图】本小题主要考查函数、导数、不等式证明等知识,通过运用导数知识解决函数、 不等式问题,考查了考生综合运用数学知识解决问题的能力以及计算能力，同时也考查了函 数与方程思想、化归与转化思想. （21）(本小题满分 12 分)（注意：在试题卷上作答无效．．．．．．．．．） 已知抛物线 2: 4C y x 的焦点为 F，过点 ( 1,0)K  的直线l 与C 相交于 A 、 B 两点， 点 A 关于 x 轴的对称点为 D . （Ⅰ）证明：点 F 在直线 BD 上； （ Ⅱ）设 8 9FA FB    ，求 BDK 的内切圆 M 的方程 . 【命题意图】本小题为解析几何与平面向量综合的问题，主要考查抛物线的性质、直线与圆 的位置关系，直线与抛物线的位置关系、圆的几何性质与圆的方程的求解、平面向量的数量 积等知识,考查考生综合运用数学知识进行推理论证的能力、运算能力和解决问题的能力， 同时考查了数形结合思想、设而不求思想.. （22）(本小题满分 12 分)（注意：在试题卷上作答无效．．．．．．．．．） 已知数列 na 中， 1 1 11, n n a a c a   . （Ⅰ）设 5 1,2 2n n c b a    ，求数列 nb 的通项公式； （Ⅱ）求使不等式 1 3n na a   成立的 c 的取值范围 . 【命题意图】本小题主要考查数列的通项公式、等比数列的定义、递推数列、不等式等基础 知识和基本技能，同时考查分析、归纳、探究和推理论证问题的能力,在解题过程中也渗透 了对函数与方程思想、化归与转化思想的考查.