重庆高考试题分类整理数学理06排列组合与概率理 11页

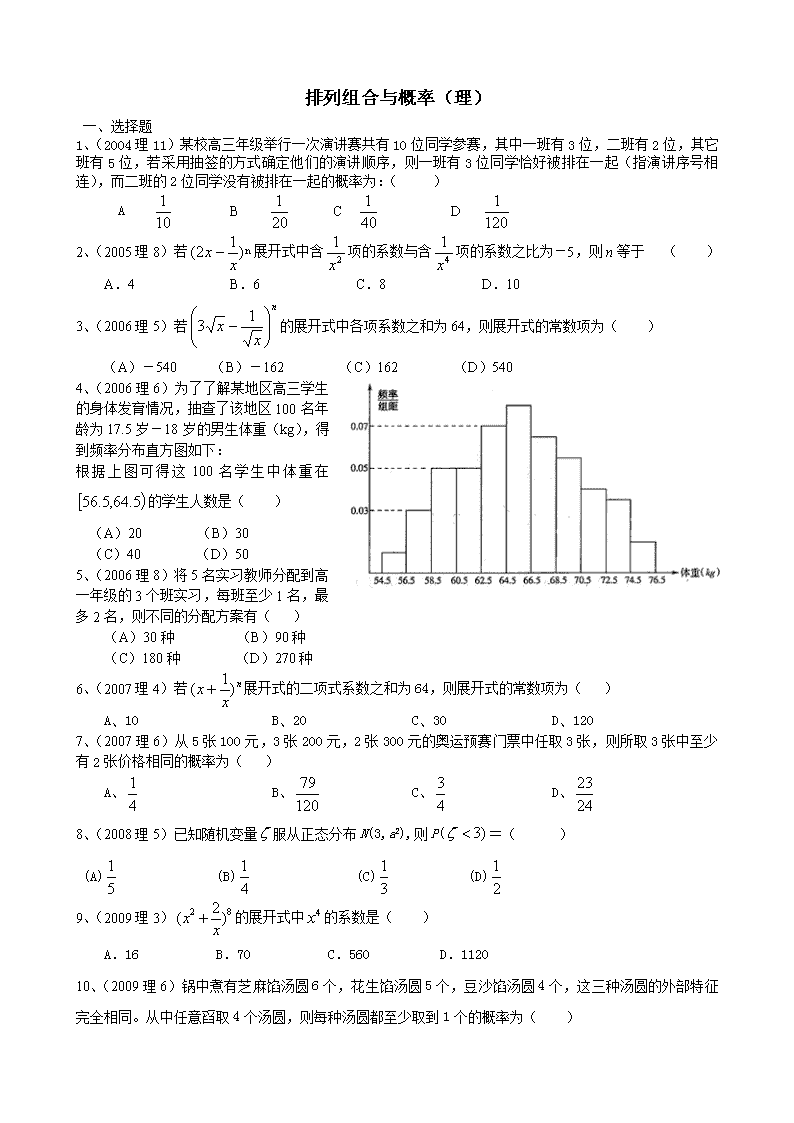
排列组合与概率（理）‎ 一、选择题 ‎1、（2004理11）某校高三年级举行一次演讲赛共有10位同学参赛，其中一班有3位，二班有2位，其它班有5位，若采用抽签的方式确定他们的演讲顺序，则一班有3位同学恰好被排在一起（指演讲序号相连），而二班的2位同学没有被排在一起的概率为：（ ）‎ ‎ A B C D ‎ ‎2、（2005理8）若n展开式中含项的系数与含项的系数之比为－5，则n等于 （ ）‎ ‎ A．4 B．‎6 ‎C．8 D．10‎ ‎3、（2006理5）若的展开式中各项系数之和为64，则展开式的常数项为（ ）‎ ‎（A）－540 （B）－162 （C）162 （D）540‎ ‎4、（2006理6）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－18岁的男生体重（kg），得到频率分布直方图如下：‎ 根据上图可得这100名学生中体重在的学生人数是（ ）‎ ‎ （A）20 （B）30 ‎ ‎ （C）40 （D）50‎ ‎5、（2006理8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（ ）‎ ‎（A）30种 （B）90种 ‎（C）180种 （D）270种 ‎6、（2007理4）若展开式的二项式系数之和为64，则展开式的常数项为（ ）‎ ‎ A、10 B、‎20 ‎ C、30 D、120‎ ‎7、（2007理6）从5张100元，3张200元，2张300元的奥运预赛门票中任取3张，则所取3张中至少有2张价格相同的概率为（ ）‎ ‎ A、 B、 C、 D、‎ ‎8、（2008理5）已知随机变量服从正态分布N(3,a2),则P(＝（ ）‎ ‎ (A) (B) (C) (D)‎ ‎9、（2009理3）的展开式中的系数是（ ）‎ A．16 B．‎70 ‎ C．560 D．1120‎ ‎10、（2009理6）锅中煮有芝麻馅汤圆6个，花生馅汤圆5个，豆沙馅汤圆4个，这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆，则每种汤圆都至少取到1个的概率为（ ）‎ A． B． C． D．‎ ‎11、（2010理9）某单位安排7位员工在‎10月1日至7日值班，每天安排1人，每人值班1天. 若7位员工中的甲、乙排在相邻两天，丙不排在‎10月1日，丁不排在‎10月7日，则不同的安排方案共有（ ）‎ ‎ A、504种 B、960种 C、1008种 D、1108种 ‎12、（2011理4）的展开式中的系数相等，则n=（ ）‎ ‎ A．6 B．‎7 ‎ C．8 D．9‎ 二、填空题 ‎13、（2004理13）若在的展开式中的系数为，则 ‎14、（2005理15）某轻轨列车有4节车厢，现有6位乘客准备乘坐，设每一位乘客进入每节车厢是等可能的，则这6位乘客进入各节车厢的人数恰好为0，1，2，3的概率为 .‎ ‎15、（2007理15）某校要求每位学生从7门课程中选修4门，其中甲、乙两门课程不能都选，则不同的选课方案有__________种.（以数字作答）‎ ‎16、（2008理16）某人有4种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡，要求同一条线段两端的灯泡不同色，则每种颜色的灯泡都至少用一个的安装方法共有 种（用数字作答）.‎ ‎17、（2009理13）将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，则不同的分配方案有 ‎ 种（用数字作答）．‎ ‎18、（2010理13）某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为，则该队员每次罚球的命中率为_____________.‎ ‎19、（2011理13）将一枚均匀的硬币投掷6次，则正面出现的次数比反面出现的次数多的概率__________。‎ 三、解答题 ‎20、（2004理18）设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯的概率为，遇到红灯（禁止通行）的概率为假定汽车只在遇到红灯或到达目的地才停止前进，表示停车时已经通过的路口数，求：‎ ‎（1）的概率的分布列及期望E;‎ ‎ (2 ) 停车时最多已通过3个路口的概率 ‎21、（2005理18）在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求：‎ ‎ （Ⅰ）该顾客中奖的概率；‎ ‎（Ⅱ）该顾客获得的奖品总价值（元）的概率分布列和期望.‎ ‎22、（2006理18）某大夏的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为，用表示这5位乘客在第20层下电梯的人数，求：‎ ‎ （I）随机变量的分布列;‎ ‎ （II）随机变量的期望;‎ ‎23、（2007理18）某单位有三辆汽车参加某种事故保险.单位年初向保险公司缴纳每辆900元的保险金，对在一年内发生此种事故的每辆汽车，单位可获9000元的赔偿（假设每辆车最多只赔偿一次）.设这三辆车在一年内发生此种事故的概率分别为1/9、1/10、1/11，且各车是否发生事故相互独立.求一年内该单位在此保险中：‎ ‎ （Ⅰ）获赔的概率；‎ ‎ （Ⅱ）获赔金额的分布列与期望.‎ ‎24、（2008理18）甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为，且各局胜负相互独立.求：‎ ‎（Ⅰ） 打满3局比赛还未停止的概率；‎ ‎（Ⅱ）比赛停止时已打局数的分别列与期望E.‎ ‎25、（2009理17）某单位为绿化环境，移栽了甲、乙两种大树各2株．设甲、乙两种大树移栽的成活率分别为和，且各株大树是否成活互不影响．求移栽的4株大树中：‎ ‎（Ⅰ）两种大树各成活1株的概率；‎ ‎（Ⅱ）成活的株数的分布列与期望．‎ ‎26、（2010理17）在甲、乙等6个单位参加的一次“唱读讲传”演出活动中，每个单位的节目集中安排在一起. 若采用抽签的方式随机确定各单位的演出顺序（序号为1，2，…，6），求：‎ ‎ （Ⅰ）甲、乙两单位的演出序号至少有一个为奇数的概率；‎ ‎ （Ⅱ）甲、乙两单位之间的演出单位个数的分布列与期望.‎ ‎27、（2011理17）某市公租房的房源位于A，B，C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的求该市的任4位申请人中：‎ ‎ （Ⅰ）恰有2人申请A片区房源的概率；‎ ‎ （Ⅱ）申请的房源所在片区的个数的分布列与期望 排列组合与概率（理）参考答案 一、选择题 ‎1、D 2、B 3、A 4、C 5、B 6、B 7、C 8、D 9、D 10、C 11、C 12、B ‎ 二、填空题 ‎13、－2 14、 15、25 16、216 17、36 18、 19、‎ 三、解答题 ‎20、解：（I）的所有可能值为0，1，2，3，4‎ ‎ 用AK表示“汽车通过第k个路口时不停（遇绿灯）”，‎ 则P（AK）=独立.‎ 故 ‎ ‎ 从而有分布列：‎ ‎ 0 1 2 3 4‎ ‎ P ‎ ‎ ‎ ‎ （II）‎ ‎ 答：停车时最多已通过3个路口的概率为.‎ ‎21、解法一： （Ⅰ），即该顾客中奖的概率为.‎ ‎（Ⅱ）的所有可能值为：0，10，20，50，60（元）.‎ ‎ ‎ ‎0‎ ‎10‎ ‎20‎ ‎50‎ ‎60‎ P 故有分布列：‎ 从而期望 解法二： （Ⅰ）‎ ‎（Ⅱ）的分布列求法同解法一 由于10张券总价值为80元，即每张的平均奖品价值为8元，从而抽2张的平均奖品价值=2×8=16（元）.‎ ‎22、解：（1）的所有可能值为0，1，2，3，4，5。‎ ‎ 由等可能性事件的概率公式得 ‎ ‎ 从而，的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎（II）由（I）得的期望为 ‎ ‎ ‎23、解：设表示第辆车在一年内发生此种事故，.‎ ‎ 由题意知独立，且.‎ ‎ （Ⅰ）该单位一年内获赔的概率为 ‎ .‎ ‎ （Ⅱ）的所有可能值为.‎ ‎ ,‎ ‎ ‎ ‎ ‎ ‎ ，‎ ‎ ‎ ‎ ‎ ‎ ，‎ ‎ .‎ ‎ 综上知，的分布列为 ‎ ‎0‎ ‎9000‎ ‎18000‎ ‎27000‎ P ‎ 求的期望有两种解法：‎ ‎ 解法一：由的分布列得 ‎ ‎ ‎24、　解：令分别表示甲、乙、丙在第k局中获胜.‎ ‎　　　　（Ⅰ）由独立事件同时发生与互斥事件至少有一个发生的概率公式知，打满3局比 赛还未停止的概率为 ‎　　　　　　　‎ ‎　　　　（Ⅱ）的所有可能值为2，3，4，5，6，且 ‎　　　　　　　‎ ‎　　　　　　　‎ ‎　　　　　　　‎ ‎　　　　　　　‎ ‎　　　　　　　‎ ‎ 　　　故有分布列 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ P ‎　　　　　　　‎ ‎　　　　　　　从而（局）.‎ ‎25、解：设表示甲种大树成活k株，k＝0，1，2‎ ‎　　表示乙种大树成活l株，l＝0，1，2‎ ‎　　则，独立. 由独立重复试验中事件发生的概率公式有 ‎ , .‎ ‎ 据此算得 ‎　　 , , .‎ ‎ , , .‎ ‎ (Ⅰ) 所求概率为　.‎ ‎ (Ⅱ) 解法一：‎ ‎　　　　的所有可能值为0，1，2，3，4，且 ‎ ,‎ ‎ ,‎ ‎ = ,‎ ‎ .‎ ‎ .‎ 综上知有分布列 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎1/36‎ ‎1/6‎ ‎13/36‎ ‎1/3‎ ‎1/9‎ 从而，的期望为（株）‎ 解法二：‎ 分布列的求法同上 令分别表示甲乙两种树成活的株数，则 故有从而知 ‎26、解：只考虑甲、乙两单位的相对位置，故可用组合计算基本事件数.‎ ‎ （Ⅰ）设A表示“甲、乙的演出序号至少一个为奇数”，则表示“甲、乙的序号为偶数”，由等可能性事件的概率计算公式得 ‎ .‎ ‎ （Ⅱ）的所有可能值为0，1，2，3，4，且 ‎ ，‎ ‎ .‎ ‎ 从而知有分布列 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎ 所以，‎ ‎ .‎ ‎27、解：这是等可能性事件的概率计算问题.‎ ‎ （I）解法一：所有可能的申请方式有34种，恰有2人申请A片区房源的申请方式种，从而恰有2人申请A片区房源的概率为 解法二：设对每位申请人的观察为一次试验，这是4次独立重复试验.‎ 记“申请A片区房源”为事件A，则 从而，由独立重复试验中事件A恰发生k次的概率计算公式知，恰有2人申请A片区房源的概率为 ‎ （II）ξ的所有可能值为1，2，3.又 综上知，ξ有分布列 ξ ‎ 1 2 3‎ P ‎ ‎ 从而有