广州市高考备考冲刺阶段数学学科训练材料理科 27页

1 2012 年广州市高考备考冲刺阶段数学学科训练材料 （理科） 说明： ⒈ 本训练题由广州市中学数学教学研究会高三中心组与广州市高考数学研究组共同编 写，共 26 题． ⒉ 本训练题仅供本市高三学生考前冲刺训练用，希望在 5 月 31 日之前完成． 3．本训练题与市高三质量抽测、一模、二模等数学试题在内容上相互配套，互为补 充．四套试题覆盖了高中数学的主要知识和方法．因此，希望同学们在 5 月 31 日至 6 月 6 日之间，安排一段时间，对这四套试题进行一次全面的回顾总结，同时，将高中数学课本中 的基本知识（如概念、定理、公式等）再复习一遍． 希望同学们保持良好的心态，在高考中稳定发挥，考取理想的成绩！ 1、已知函数 . （1）试说明函数 的图象可由函数 的图象经过怎样的变换得到； （2）写出函数 图象的对称轴方程及对称中心坐标. 2 、 在 中 ， 、 、 的 对 边 分 别 是 、 、 ， 已 知 . （1）求 的值； （2）若 的面积为 ， ，求 的值. 3、设函数 ，其中，角 的顶点与坐标原点重合，始边与 轴非负 半轴重合，终边经过点 ，且 . （1）若 点的坐标为 ，求 的值； （2）若点 为平面区域 上的一个动点，试确定角 的取值范围，并求函数 的最小值和最大值. ( ) 4cos sin 33f x x x π = + −   )(xfy = xy 2sin2= )(xf ABC∆ A B C a b c b ac B CA −=− 3 cos cos3cos a c ABC∆ 2 3 3cos =B b ααα cos3sin)( +=f α x ),( yxP πα ≤≤0 P )1,3( )(αf ),( yxP    ≤ ≥ ≥+ 1 1 y xy yx α )(αf 2 4、已知关于 的一元二次函数 （1）设集合 P={1，2， 3}和 Q={－1，1，2，3，4}，分别从集合 P 和 Q 中随机取一个数 作为 和 ，求函数 在区间[ 上是增函数的概率； （2）设点（ ， ）是区域 内的随机点，求函数 上 是增函数的概率． 5、今天你低碳了吗？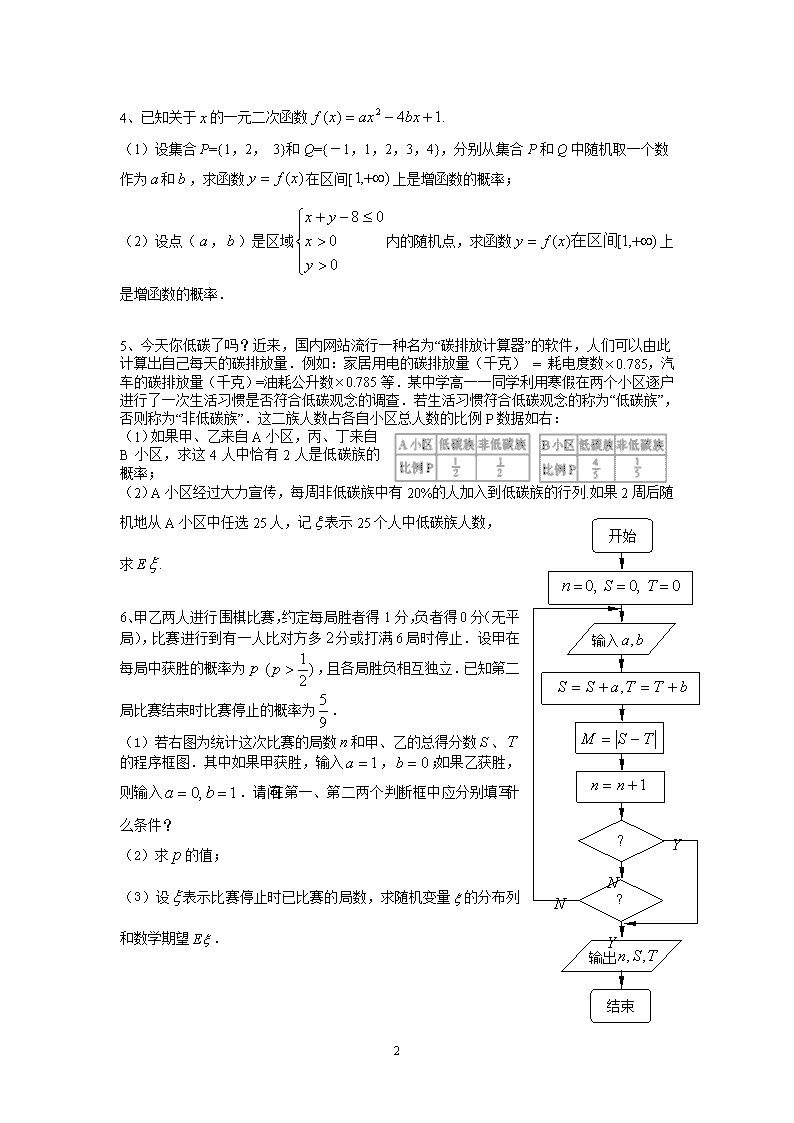近来，国内网站流行一种名为“碳排放计算器”的软件，人们可以由此 计算出自己每天的碳排放量．例如：家居用电的碳排放量（千克） = 耗电度数 0.785，汽 车的碳排放量（千克）=油耗公升数 0.785 等．某中学高一一同学利用寒假在两个小区逐户 进行了一次生活习惯是否符合低碳观念的调查．若生活习惯符合低碳观念的称为“低碳族”， 否则称为“非低碳族”．这二族人数占各自小区总人数的比例 P 数据如右： （1）如果甲、乙来自 A 小区，丙、丁来自 B 小区，求这 4 人中恰有 2 人是低碳族的 概率； （2）A 小区经过大力宣传，每周非低碳族中有 20%的人加入到低碳族的行列.如果 2 周后随 机地从 A 小区中任选 25 人，记 表示 25 个人中低碳族人数， 求 E .[Z&xx 6、甲乙两人进行围棋比赛，约定每局胜者得 1 分，负者得 分（无平 局），比赛进行到有一人比对方多 分或打满 局时停止．设甲在 每局中获胜的概率为 ，且各局胜负相互独立．已知第二 局比赛结束时比赛停止的概率为 ． （1）若右图为统计这次比赛的局数 和甲、乙的总得分数 、 的程序框图．其中如果甲获胜，输入 ， ；如果乙获胜， 则输入 ．请问在第一、第二两个判断框中应分别填写什 么条件？ （2）求 的值； （3）设 表示比赛停止时已比赛的局数，求随机变量 的分布列 和数学期望 ． × × ξ ξ x .14)( 2 +−= bxaxxf a b )(xfy = ),1 +∞ a b    > > ≤−+ 0 0 08 y x yx ),1[)( +∞= 在区间xfy 0 2 6 p )2 1( >p 9 5 n S T 1=a 0=b 1,0 == ba p ξ ξ Eξ 输入 ba, 开始 bTTaSS +=+= , 0,0,0 === TSn 结束 输出 TSn ,, Y TSM −= 1+= nn ? Y N N ? 3 7、如图，一个圆锥和一个圆柱组成了一个几何体，其中圆锥和圆柱 的的底面半径相同，点 ， ，分别是圆柱的上下底面的圆心， ， 都为直径，点 五点共面，点 是弧 AB 上的任 意一点（点 与 不重合），点 为 的中点， 是弧 CD 上一点，且 // ， ． （1）求证： ⊥平面 ； （2）求证：平面 //平面 ； （3）若点 N 为弧 AB 的三等分点且 ，求面 ANP 与面 POM 所成角的正弦值． 8、如图，在直棱柱 中， ， ，延长 至 ， 使 ，连结 ． （1） ； （2）求五面体 的体积． （3）求平面 与平面 所成锐二面角 的正切值． 9、如图，矩形 与 所在平面互相垂直（如图①），将矩形 沿 对折， 使得翻折后点 落在线段 上（如图②），设 ， ， . (1) 试求 关于 的函数解析式； (2) 当 取最小值时，指出点 的位置，并求出此时 与平面 所成的角； (3) 在条件(2)下，求三棱锥 P-ADQ 内切球的半径． O O′ AB CD DCBAP ,,,, N N BA, M BN N′ NN ′ AD 2=== BCABPA BN POM POM DNAN ′  1= 3AN AB 1 1 1ABC A B C− AC BC⊥ 1 1AC BC AA= = = AC D AC CD= 1 1, , ,BD B D CD C D 1 1AC B D⊥ 1 1 1BB A ADC− 1 1B C D ABC ABCD ADQP ADQP PD Q BC 1=AB hPA = yAD = y h y Q AD PDQ ⇒ 图① 图② A C CA B D B 1 11 4 10、提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车 流速度 （单位：千米/小时）是车流密度 （单位：辆/千米）的函数．当桥上的车流密 度达到 200 辆/千米时，造成堵塞，此时车流速度为 0 ；当车流密度不超过 20 辆/千米时， 车流速度为 60 千米/小时．研究表明：当 时，车流速度 是车流密度 的一次 函数． (1)当 时，求函数 的表达式； (2)当车流密度 为多大时，车流量 可以达到最大，并求出最大值（精确到 1 辆/小时）. (车流量为单位时间内通过桥上某观测点的车辆数，单位：辆/小时） 11、某地政府为改善居民的住房条件，集中建设一批经适楼房．用了 1400 万元购买了一块 空地，规划建设 8 幢楼，要求每幢楼的面积和层数等都一致，已知该经适房每幢楼每层建筑 面积均为 250 平方米，第一层建筑费用是每平方米 3000 元，从第二层开始，每一层的建筑 费用比其下面一层每平方米增加 80 元． （1）若该经适楼房每幢楼共 层，总开发费用为 万元，求函数 的表达 式（总开发费用=总建筑费用+购地费用）； （2）要使该批经适房的每平方米的平均开发费用最低，每幢楼应建多少层？ (参考数据： ) 12、已知双曲线的中心在原点,右顶点为 A(1,0).点 P、Q 在双曲线的右支上,已知圆 与直线 AP 相切,圆心为 M. (1)若直线 AP 的斜率为 k，且 ,求实数 m 的取值范围； (2)当 时,ΔAPQ 的内心恰好是点 M，求此双曲线的方程. 13、已知动圆过定点 ，且与直线 相切，记动圆圆心的轨迹为曲线 ． （1）求曲线 的方程； （2）若点 、 、 是曲线 上的不同三点，且满足 ．证明：△ 不可能是直角三角形． v x 20020 ≤≤ x v x 2000 ≤≤ x ( )xv x )()( xvxxf ⋅= x ( )y f x= ( )y f x= 5 2.236, 6 2.449, 7 2.646≈ ≈ ≈ 2 2( ) 1x m y− + = ( )m R∈ 2 3[ , ]4 3k ∈ 3m = ( )1,0F 1x = − Γ Γ A B C Γ FA FB FC+ + = 0   ABC 5 14、给定椭圆 ： ，称圆心在原点 、半径为 的圆是椭 圆 的“准圆”.若椭圆 的一个焦点为 ，其短轴上的一个端点到 的距离为 . （1）求椭圆 及其“准圆”的方程； （2）设点 是椭圆 的“准圆”上的一个动点，过点 任作两条直线 、 ，使得 、 与椭圆 都只有一个公共点，试判断 与 是否垂直？并说明理由. 15、如图，已知抛物线 ： 和⊙ ： ，过抛物线 上一点 作两条直线与⊙ 相切于 、 两点，分 别交抛物线为 E、F 两点，圆心点 到抛物线准线的距离为 ． （1）求抛物线 的方程； （2）当 的角平分线垂直 轴时，求直线 的斜率； （3）若直线 在 轴上的截距为 ，求 的最小值． 16、已知椭圆 ： ， 分别为左，右焦点，离心率为 ，点 在椭圆 上， ， ，过 与坐标轴不垂直的直线交椭圆 于 两点． （1）求椭圆 的方程； （2）在线段 上是否存在点 ,使得以线段 为邻边的四边形是菱形？若 存在,求出实数 的取值范围；若不存在，说明理由． 17、已知函数： ． （1）讨论函数 的单调性； （2）若函数 的图象在点 处的切线的倾斜角为 45o，是否存在实数 m 使得 对于任意的 ，函数 在区间 上总不是单调函数? 若存在，求 m 的取值范围；否则，说明理由； O C F 3 P C P C 2 2 2 2 1 ( 0)x y a ba b + = > > 2 2a b+ C ( 2,0)F C 1l 2l 1l 2l C 1l 2l C pxy 22 = M 1)4( 22 =+− yx C )1)(,( 000 ≥yyxH M A B M 4 17 C AHB∠ x EF AB y t t C )0(12 2 2 2 >>=+ bab y a x 21, FF 2 1 A C 21 =AF AFAFAFAF 1212 2 ⋅−= 2F QP, C 2OF )0,(mM MQMP, m ( ) Raaxxaxf ∈−−= ,3ln )(xf )(xfy = ( ))2(,2 f [ ]2,1∈t ]2)([)( 23 mxfxxxg +′+= ( )3,t 6 （3）求证： （ 且 ）． 18、记函数 在区间 D 上的最大值与最小值分别为 与 ．设函数 ，1 ( )xf ( ){ }Dxxf ∈max ( ){ }Dxxf ∈min ( ) [ ] ( ]   ∈ ∈+−= 3,, ,1,2 bxb bxbxxf ( ) ( ) [ ]3,1, ∈+= xaxxfxg )(xg [ ]3,1 10 ≤≤ a ( ) ( ){ }3,1max ∈bbd 2( ) ( 2) ln .f x x a x a x= − + + 0a > 2a > ( )f x 4a = 6 0x y m+ + = 3 0x y n− + = ,m n ( )y f x= m n D ( )y h x= 0 0( , ( ))P x h x : ( )l y g x= 0x x≠ 0 ( ) ( ) 0h x g x x x − >− D P ( )y h x= 4a = ( )y f x= )(xf ],[ ba bxxxxxaT nii =<<<<<<= −  110: ],[ ba n 0>M Mxfxf n i ii ≤−∑ = − 1 1)()( ni ,,2,1 = )(xf ],[ ba ],[ baBVf ∈ ],[ baBV ],[ ba 2)( xxf = ]1,0[ )(xf ],[ ba ],[ baBVf ∈ ],[ ba )(xf k 1x ],[2 bax ∈ 7 .证明： . 21 、已知定义在 上的单调函数 ，存在实数 ，使得对于任意实数 ，总有 恒成立． （1）求 的值； （2）若 ，且对任意正整数 ，有 ， 记 ，比较 与 的大小关系，并 给出证明． 22、如图,已知直线 及曲线 上的点 的横坐标为 ( ).从曲 线 C 上的点 作直线平行于 轴，交直线 作直线平行于 轴， 交曲线 的横坐标构成数列 . (1)试求 的关系； (2)若曲线 C 的平行于直线 的切线的切点恰好介于点 之间 (不与 重合),求 的取值范围； (3)若 ,求数列 的通项公式. 23、已知函数 ，设 在点 N*）处的切线在 轴上的截 距为 ，数列 满足： N*）． （1）求数列 的通项公式； （2）在数列 中，仅当 时， 取最小值，求 的取值范围； （3）令函数 ，数列 满足： ， N*）， 求证：对于一切 的正整数，都满足： ． 2121 )()( xxkxfxf −⋅≤− ],[ baBVf ∈ R ( )f x 0x 1 2,x x 0 1 0 2 0 1 2( ) ( ) ( ) ( )f x x x x f x f x f x+ = + + 0x 0( ) 1f x = n 1 1, ( ) 1( ) 2n n na b ff n = = + 1 2 2 3 1 1 2 2 3 1,n n n n n nS a a a a a a T bb b b b b+ += + + + = + + +  4 3 nS nT : 4l y x= 2: ,C y x C= 1Q 1a 10 4a< < ( 1)nQ n ≥ x 1 1n nl P P+ +于点 ，再从点 y 1. ( 1,2,3,n nC Q Q n+ =于点 …） { }na 1n na a+ 与 l 1 2,Q Q 1 2,Q Q 3a 1 3a = { }na ( ) ( 0)1 xf x xx = >+ ( )f x ( , ( ))(n f n n∈ y nb { }na 1 1 1 , ( )(2 n na a f a n+= = ∈ { }na       + nn n aa b λ 2 5=n nn n aa b λ+2 λ 2( ) ( )(1 )g x f x x= + { }nc 1 1 2c = 1 ( )(n nc g c n+ = ∈ 2≥n 21 1 1 1 1 11 21 <++++++< nccc  y xO a1a2a3 Q1 Q2 Q3 P2 P3 8 24、设首项为 的正项数列 的前 项和为 , 为非零常数,已知对任意正整数 , 总成立. 学科网 （1）求证：数列 是等比数列； 学科网 （2）若不等的正整数 成等差数列，试比较 与 的大小； 学科网 （3）若不等的正整数 成等比数列，试比较 与 的大小. 学科网 25、已知数列 满足： ， ，数列 满 足 ． (1)求数列 的通项公式； (2)证明:数列 中的任意三项不可能成等差数列． 26、已知正项数列 的前 项和为 ，且函数 在 处的切线的 斜率为 . (1) 求数列 的通项公式； (2) 求证： ； (3) 是否存在非零整数 ，使不等式 对一切 都成立？若存在，求出 的值；若不存在，说明理由. 1a { }na n nS q ,n m m n m m nS S q S+ = + { }na , ,m k h m h m ha a⋅ 2k ka , ,m k h 1 1 m h m ha a⋅ 2 k ka { }na 1 1 1 1 )1(2 1 )1(3,2 1 + + − +=− += n n n n a a a aa )1(01 ≥<⋅ + naa nn { }nb )1(22 1 ≥−= + naab nnn { }na { }nb { }nb { }na n nS ( ) ln 4 xf x x= + nx a= 2 n n S a *( )n∈N { }na 3 3 3 3 1 2 3 1 1 1 1 5 32na a a a + + + + < *( )n∈N λ 1 1 2 1 1 1 1(1 )(1 ) (1 )cos 2 1 n n n a a a a a πλ +− − ⋅ ⋅ − < + *n∈N λ 9 2012 年广州市高考备考冲刺阶段数学学科(理科)训练材料参考答案 1、（1） ． 故函数 的图象可由函数 的图象向左平移 得到. （2）由 ，得 ， ， 故函数 的图象的对称轴方程为 ， . 由 ，得 ， ， 故函数 的图象的对称中心为 ， . 2、（1）由正弦定理得 ， ， ， 所以 ， 即 ， 即有 ， 又 ，所以 ，所以 ． （2）由（1）知 ， 又 ， ，所以 . 又 的 面 积 为 ， 所 以 ， 即 ， 得 ， .由余弦定理得： ， 所以 . 3)3sin(cos4)( −+= π xxxf 3)2cos2 32sin2 1(cos4 −+= xxx 3cos322sin 2 −+= xx 32 2cos1322sin −+×+= xx xx 2cos32sin += 2sin 2 3x π = +   )(xfy = xy 2sin2= 6 π πππ kx +=+ 232 212 ππ kx += k ∈Z )(xf 212 ππ kx += k ∈Z ππ kx =+ 32 26 ππ kx +−= k ∈Z )(xf ,06 2 kπ π − +   k ∈Z ARa sin2= BRb sin2= CRc sin2= B AC b ac B CA sin sinsin33 cos cos3cos −=−=− BABCBCBA cossincossin3sincos3sincos −=− )sin(3)sin( CBBA +=+ π=++ CBA AC sin3sin = 3sin sin == A C a c ac 3= 3 3cos =B π<< B0 3 6sin =B ABC∆ 2 2sin2 1 =Bac 23 6 2 3 2 =×a 2=a 6=c 43 362226cos2222 =××−+=−+= Bacacb 2=b 10 3、（1）由三角函数的定义，得 ， ， 故 . （2）作出平面区域 （即三角形区域 ）如图所示， 其中 ， ， ，于是 . 又 ，且 , 故当 ，即 时， 取得最小值，且最小值为 1． 当 ，即 时， 取得最大值，且最大值为 . 4、（1）∵函数 的图象的对称轴为 要使 在区间 上为增函数， 当且仅当 >0 且 ． 若 =1 则 =－1；若 =2 则 =－1，1； 若 =3 则 =－1，1； ∴事件包含基本事件的个数是 1+2+2=5 ∴所求事件的概率为 ． （2）由（Ⅰ）知当且仅当 且 >0 时， 函数 上为增函数， 依条件可知试验的全部结果所构成的区域为 ． 构成所求事件的区域为三角形部分，由 ∴所求事件的概率为 ． 2 1sin =α 2 3cos =α 22 332 1cos3sin)( =×+=+= αααf Ω ABC )1,0(A )2 1,2 1(B )1,1(C 24 παπ ≤≤ )3sin(2cos3sin)( παααα +=+=f 6 5 312 7 ππαπ ≤+≤ 6 5 3 ππα =+ 2 πα = )(αf 12 7 3 ππα =+ 4 πα = )(αf 2 62 + 14)( 2 +−= bxaxxf ,2 a bx = 14)( 2 +−= bxaxxf ),1[ +∞ a aba b ≤≤ 2,12 即 a b a b a b 5 1 15 3 = ab ≤2 a ),1[14)( 2 +∞+−= 在区是间bxaxxf 8 0 ( , ) 0 0 a b a b a b  + − ≤   >     >  ),3 8,3 16( 2 08 得交点坐标为    = =−+ ab ba 3 1 882 1 3 882 1 = ×× ×× =P x y o A B C•P 11 5、（1）记这 4 人中恰好有 2 人是低碳族为事件 A， P(A)= ． （2）设 A 小区有 人，2 周后非低碳族的概率 ， 2 周后低碳族的概率 = ， 依题意 ~B(25， )，所以 E =25 =17． 6、（1）程序框图中的第一个条件框应填 ，第二个应填 ． 注意：答案不唯一． 如：第一个条件框填 ，第二个条件框填 ，或者第一、第二条件互换．都可以． （2）依题意，当甲连胜 局或乙连胜 局时，第二局比赛结束时比赛结束． 有 ． 解得 或 ． ， ． （3）依题意知，依题意知， 的所有可能值为 2，4，6． 设每两局比赛为一轮，则该轮结束时比赛停止的概率为 ． 若该轮结束时比赛还将继续，则甲、乙在该轮中必是各得一分，此时，该轮比赛结果对下轮 比赛是否停止没有影响． 从 而 有 ， 　 ， ． 随机变量 的分布列为： 2 4 6 P 故 ． 7、（1）连结 ， ∵ , 为 的中点， ∴△ONB 中， ⊥ ． ∵ , 为 的中点， ∴△PNB 中， ⊥ ． 又∵ = 且 OM、PM 在平面 POM 内， 100 33 5 4 5 4 2 1 2 1 5 1 5 4 2 1 2 145 1 5 1 2 1 2 1 =×××+××××+××× 25 17 25 81 =− ξ 25 17 ξ × 25 17 a 25 8)5 11(2 2 1 = − = a a p p 2=M 6=n 1>M 5>n 2 2 ∴ 9 5)1( 22 =−+ pp 3 2=p 3 1=p 2 1>p 3 2=∴ p ξ 9 5 5( 2) 9P ξ = = 81 20)9 5)(9 51()4( =−==ξP 81 161)9 51)(9 51()6( =⋅−−==ξP ∴ ξ ξ 9 5 81 20 81 16 5 20 16 2662 4 69 81 81 81Eξ = × + × + × = ON OBON = M BN BN OM PBPN = M BN BN PM OM  PM M 12 ∴ ⊥平面 ． （2）连结 ， ∵点 ， 分别为 ， 的中点， ∴△ABN 中， // ． ∵AN 在平面 内，OM 在平面 外， ∴OM∥平面 ． 又∵ // ， 在平面 内，PO 在平面 外， ∴PO∥平面 ． ∵OM、PO 在平面 POM 内，且 = ， ∴平面 //平面 ． （3）过点 P 作直线 ∥OM，∵点 P 在平面 POM 内，∴ 在平面 POM 内． 又∵AN∥OM， ∴直线 ∥AN， ∴ 在平面 PAN 内. ∴ 为平面 PAN 与平面 POM 的交线， 取 AN 中点 E，连接 PE、EO， ∵PA=PN ∴PE⊥AN ∴PE⊥直线 ， 又∵PO⊥OM ∴PO⊥直线 ． ∴∠EPO 为平面 PAN 与平面 POM 所成角. 当弧 AN= 弧 AB 时，AN=AO=1 ，∴直角三角形 PAE 中， ， 三角形 ANO 中，OE= ， ∴直角三角形 POE 中， . 8、（1）在 中， ，所以 ， 故 ，即 。 在直棱柱 中， ， ， ， 所以 ， ，即 平面 。 又 平面 ，所以 。 所以 平面 ，即 。 （2）五面体 的体积 。 （3）作 ，且 。因为 ，所以 。 BN POM AN O M AB BN OM AN DNAN ′ DNAN ′ DNAN ′ PO NN ′ NN ′ DNAN ′ DNAN ′ DNAN ′ OM  PO O POM DNAN ′ l l l l l l l 3 1 2 15 2 12 2 222 =    −=−= AEPAPE 2 3 5 5sin ==∠ PE EOEPO 1AC D∆ 1 1 1AC DC AA CC= = = = 1 1 2, 2AC C D AD= = = 2 2 2 1 1AD AC C D= + 1 1AC C D⊥ 1 1 1ABC A B C− AC BC⊥ 1 1 //AC AC 1 1 //B C BC 1 1 1 1B C AC⊥ 1 1 1B C CC⊥ 1 1B C ⊥ 1 1A ACC 1AC ⊂ 1 1A ACC 1 1AC B C⊥ 1AC ⊥ 1 1B C D 1 1AC B D⊥ 1 1 1BB A ADC− 1 1 1 1 1 1 1 1 1 1 1 5 2 3 2 3 6ABC A B C D BB C CV V V AC BC AA BC AA CD− −= + = × × + × × × = + = //DF BC DF BC= AC BC⊥ DF AD⊥ 13 又 平面 ， ，所以 平面 ，即 。 由 ，得 。 所以 为平面 与平面 所成锐二面角的平面角。 所以平面 与平面 所成锐二面角的正切值为 。 （也可用空间向量求得平面 与平面 所成锐二面角的正切值为 1） 9、(1)显然 ，连接 ，∵ ， ， ∴ .由已知 ， ∴ ， . ∵ ∽ ， ， ∴ 即 . ∴ . (2) 当且仅当 时，等号成立.此时 ，即 为 的中点. 于是由 ，知平面 ， 是其交线，则过 作 AE⊥PQ 于 E，∴ ． ∴ 就是 与平面 所成的角. 由已知得 ， ， ∴ ， , . (3) 设三棱锥 的内切球半径为 ，则 ∵ ， ， ， ， ， 1 1B C ⊥ 1 1A ACC 1 1 //B C BC BC ⊥ 1 1A ACC 1BC C D⊥ //DF BC 1DF C D⊥ 1ADC∠ 1 1B C D ABC 1 1B C D ABC 1 1tan 1CCADC CD ∠ = = 1 1B C D ABC 1>h AQ ADQPABCD 平面平面 ⊥ ADPA ⊥ ABCDPA 平面⊥ DQPQ ⊥ DQAQ ⊥ 222 hyAQ −= ABQRt∆ QCDRt∆ 12 −= hCQ AB CQ AQ DQ = 1 12 22 −= − h hy h )1( 12 2 > − = h h hy 2 1 11 1 1)1( 1 2 2 2 2 2 2 h h h h h hy ≥ − +−= − +− − = 2h, 1h 11h 2 2 = − =− 即 1=CQ Q BC PAQDQ 平面⊥ PAQPDQ 平面⊥ PQ A PDQAE 平面⊥ ADE∠ AD PDQ 2=AQ 2== ADPQ 1=AE 2 1sin ==∠ AD AEADE 030=∠ADE ADQP − r ADQPADQPDQPAQPAD VrSSSS −∆∆∆∆ =⋅+++ )(3 1 3 2 3 1 =⋅= ∆− PASV ADQADQP 1=∆PAQS 2=∆PADS 1=∆QADS 2=∆PDQS 14 ∴ . 10、(1)由题意，当 时， 当 时，设 由已知得 解得 . . (2)依题意得 当 时， 为增函数，故 . 当 时， 时， 取最大值 . 答：车流密度 为 100 时，车流量 达到最大值 3333. 11、（1）由已知，每幢经适楼房最下面一层的总建筑费用为： （元） （万元）， 从第二层开始，每幢每层的建筑总费用比其下面一层多： （元） （万元）， 每幢经适楼房从下到上各层的总建筑费用构成以 75 为首项，2 为公差的等差数列， 所以函数表达式为： ． （2）由（1）知经适楼房每平方米平均开发费用为： （元） 当且仅当 ，即 时等号成立， 但由于 ，验算：当 时， ， 当 时， ． 由于 ， 2 22 222 2 −= + =r 0 20x≤ ≤ ( ) 60;v x = 20 200x≤ ≤ ( ) .v x ax b= + 200 0,20 60 a b a b + =  + = 1 3 200 3 a b  = −  = 60,0 20 ( ) 1 (200 ),20 2003 x v x x x ≤ <∴ =  − ≤ ≤ 60 ,0 20 ( ) .(200 ),20 2003 x x f x x x x ≤ <=  − ≤ ≤ 0 20x≤ ≤ ( )f x ( ) 1200f x < 20 200x≤ ≤ 100x = ( )f x 10000 33333 ≈ x ( )f x 3000 250 750000× = 75= 80 250 20000× = 2= 2 *( 1)( ) 8[75 2] 1400 8 592 1400 ( )2 x xy f x x x x x −= = + × + = + + ∈N 2( ) 40( 74 175)( ) 100008 250 f x x xg x x x + += × =× ( )17540 74 40 2 175 74x x  = + + +  ≥ 175x x = 13.2x ≈ *x∈N 13x = 175( ) 40 13 7413g x  = + +   14x = 175( ) 40 14 7414g x  = + +   17540 13 7413  + + <   17540 14 7414  + +   15 所以 时，每平方米平均开发费用最小. 答：该经适楼建为 13 层时，每平方米平均开发费用最低． 12、(1)由条件得直线 AP 的方程 即 因为点 M 到直线 AP 的距离为 1,∴ 即 . ∵ ∴ 解得-2≤m≤-1 或 3≤m≤4. ∴m 的取值范围是 (2)设双曲线方程为 由 得 . 在等式 中,由 ,解出 . 又因为 M 是 ΔAPQ 的内心，所以，直线 AM 是∠PAQ 的角平分线，且 M 到 AQ、PQ 的距离 均为 1.因此 (不妨设 P 在第一象限)，直线 PQ 方程为 .直线 AP 的方程 ，∴解得 P 的坐标是(4, )，将 P 点坐标代入 得, , 所以所求双曲线方程为 . 13、（1）设动圆圆心的坐标为 ，动圆半径为 . 因为动圆过定点 ，所以 . 因为动圆与直线 相切，所以 . 消去 得 ，化简得 . 所以曲线 的方程为 . （2）假设△ 是直角三角形，不失一般性，设 ，则 . 设 ， ， . 13x = ),1( −= xky .0=−− kykx ,1 12 = + − k kmk 2 2 1111 kk km +=+=− 2 3[ , ]4 3k ∈ 2 1 3,m≤ − ≤ [ 2, 1] [3,4].− −  ),0(12 2 2 ≠=− bb yx (3,0), (1,0),M A 2AM = 2 11 1m k − = + 3m = 3 3k = ± 3 3,3 3AP AQk k= = − 4x = ( )3 13y= x- 3 12 2 2 =− b yx 2 1 5b = 2 25 1x y− = ( , )x y r ( )1,0F 2 2( 1)x y r− + = 1x = − 1x r+ = r 2 2( 1) 1x y x− + = + 2 4y x= Γ 2 4y x= ABC 090A∠ = 0AB AC⋅ =  1 1( , )A x y 2 2( , )B x y 3 3( , )C x y 16 由于 、 、 是曲线 上的不同三点，所以 （ ）， ， . 因为 ，所以 ， 解得 ， . 由 ，得 . 把 （ ）代入上式，化简得 ， 所以 ，即 ，所以 . 因为 ，所以 ， 把 ， 代入上式，化简得 . 因为△＝ ，所以 无解，这与点 是曲线 上的点矛盾. 所以△ 不可能是直角三角形． 14、（1）设椭圆 的半焦距为 ，则 ， ， 所以 ，“准圆”的半径 . 所以椭圆 的方程为 ，“准圆”的方程为 . （2）由于直线 、 的斜率可能存在，也可能不存在，下面分两种情况加以讨论. ①当 、 中至少有一条直线的斜率不存在时，不妨设 的斜率不存在. 因为 与椭圆 只有一个公共点，所以 的方程为 . 当 的方程为 时，此时 与“准圆”交于 、 两点. 此时经过点 且与椭圆 只有一个公共点的另一条直线是 ， 经过点 且与椭圆 只有一个公共点的另一条直线是 . 2 4 i i yx = 1 2y y≠ 1 3y y≠ 1 2 3 3x x x+ + = 1 2 3 0y y y+ + = 2 1 3 1 2 1 3 1( )( ) ( )( ) 0x x x x y y y y− − + − − = 2 4 i i yx = 1l 1l 1l 1l 1l A B C Γ 1,2,3i = FA FB FC+ + = 0   1 1 2 2 3 3( 1, ) ( 1, ) ( 1, ) (0,0)x y x y x y− + − + − = 0AB AC⋅ =  1,2,3i = 1 2 1 3( )( ) 16y y y y+ + = − 3 2( ) ( ) 16y y− ⋅ − = − 3 2 16y y = − 1 2 3 2 2 16y y y y y = − − = − + 22 2 31 2 1 2 3 34 4 4 yy yx x x+ + = + + = 2 2 2 1 2 3 12y y y+ + = 1 2 2 16y y y = − + 3 2 16y y = − 4 2 2 222 256 0y y− + = 2( 22) 4 256 540 0− − × = − < 2y B Γ ABC C c 2c = 3a = 2 2 1b a c= − = 2 2 2r a b= + = C 2 2 13 x y+ = 2 2 4x y+ = 1l 2l 1l 2l C 3x = ± 3x = ( 3,1) ( 3, 1)− ( 3,1) C 1y = ( 3, 1)− C 1y = − 17 即 的方程是为 或 ，显然 . 同理可证，当 的方程为 时，也有 . ②当 、 的斜率都存在时，设 、 的斜率分别为 、 . 设 ，则 . 设经过点 且与椭圆只有一个公共点的直线方程为 . 由 消去 得 . 由△ ， 整理得 . 因为 ，所以上式可化为 . 因为 、 与椭圆 都只有一个公共点， 所以 、 满足方程 ， 所以 ，所以 . 综上①与②可知， . 15、（1）∵点 到抛物线准线的距离为 ， ∴ ，即抛物线 的方程为 ． （2）法一：∵当 的角平分线垂直 轴时，点 ，∴ ， 设 ， ， ∴ ， ∴ ， ∴ . ． 法二：∵当 的角平分线垂直 轴时，点 ，∴ ，可得 ， 1l 2l 1y = 1y = − 1 2l l⊥ 3x = − 1 2l l⊥ 1l 2l 1l 2l 1k 2k 0 0( , )P x y 2 2 0 0 4x y+ = 0 0( , )P x y 0 0( )y y k x x− = − 0 0 2 2 ( ), 1,3 y y k x x x y − = − + = y 2 2 2 0 0 0 0(1 3 ) 6 ( ) 3( ) 3 0k x k y kx x y kx+ + − + − − = 2 2 2 0 0 0 0[6 ( )] 4(1 3 )[3( ) 3] 0k y kx k y kx= − − + − − = 2 2 2 0 0 0 0(3 ) 2 1 0x k x y k y− + + − = 2 2 0 0 4x y+ = 2 2 2 0 0 0 0(3 ) 2 3 0x k x y k x− + + − = 1l 2l C 1k 2k 2 2 2 0 0 0 0(3 ) 2 3 0x k x y k x− + + − = 2 0 1 2 2 0 3 13 xk k x −⋅ = = −− 1 2l l⊥ 1 2l l⊥ M =+ 24 p 4 17 2 1=p C xy =2 AHB∠ x )2,4(H HE HFk k= − 1 1( , )E x y 2 2( , )F x y 1 2 1 2 H H H H y y y y x x x x − −= −− − 1 2 2 2 2 2 1 2 H H H H y y y y y y y y − −= −− − 1 2 2 4Hy y y+ = − = − 2 1 2 1 2 2 2 1 2 1 2 1 1 1 4EF y y y yk x x y y y y − −= = = = −− − + AHB∠ x )2,4(H 60=∠AHB 3=HAk 18 ，∴直线 的方程为 ， 联立方程组 ，得 ， ∵ ∴ ， ． 同理可得 ， ，∴ ． （3）法一：设 ，∵ ，∴ ， 可得，直线 的方程为 ， 同理，直线 的方程为 ， ∴ ， ， ∴直线 的方程为 ， 令 ，可得 ， ∵ 关于 的函数在 单调递增， ∴ ． 法二：设点 ， ， ． 以 为圆心， 为半径的圆方程为 ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙① ⊙ 方程： ． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙② ①-②得： 直线 的方程为 ． 当 时，直线 在 轴上的截距 ， ∵ 关于 的函数在 单调递增， ∴ ． 16、（1）由已知 ，所以 ， ， ． 3−=HBk HA 2343 +−= xy    = +−= xy xy 2 2343 02343 2 =+−− yy 32 3Ey + = 3 63 −=Ey 3 3413 −=Ex 3 63 −−=Fy 3 3413 +=Fx 4 1−=EFk ),(),,( 2211 yxByxA 41 1 −= x ykMA 1 14 y xkHA −= HA 0154)4( 111 =−+−− xyyxx HB 0154)4( 222 =−+−− xyyxx 0154)4( 101 2 01 =−+−− xyyyx 0154)4( 202 2 02 =−+−− xyyyx AB 0 2 2 0 0(4 ) 4 15 0y x y y y− − + − = 0=x )1(154 0 0 0 ≥−= yyyt t 0y [1, )+∞ 11min −=t 2( , )( 1)H m m m ≥ 2 4 27 16HM m m= − + 2 4 27 15HA m m= − + H HA 2 2 2 4 2( ) ( ) 7 15x m y m m m− + − = − + M 1)4( 22 =+− yx AB 2 2 4 2(2 4)(4 ) (2 ) 7 14x m m y m m m m− − − − − = − + 0x = AB y 154t m m = − ( 1)m ≥ t m [1, )+∞ 11min −=t 2 1=e ac =2 21 =AF 222 −= aAF 19 又因为 ，所以 ， 由余弦定理 ， 所以 ， ，所以椭圆方程为 ． （ 2 ） 假 设 存 在 点 满 足 条 件 ， 设 ， ， 直 线 的 方 程 为 ， 联立： ， 有： 由题知 ， 由 ， 有 ， 即 ， 则 ， 所以 ， ， 又 在线段 上，则 ， 故存在 满足题意． 17、（1） ， 当 a>0时， 的单调增区间为 ，减区间为 ； 当 a<0时， 的单调增区间为 ，减区间为 ； 当 a=0时， 为常函数． AFAFAFAF 1212 2 ⋅−= 2 1cos 21 =∠ AFF 20442 1)22(22)22(4 222 =⇒=+−⇒×−×−−+= aaaaaa 1=c 3222 =−= cab 134 22 =+ yx )0,(mM ),( 11 yxP ),( 22 yxQ )1( −= xky 01248)43(1243 )1( 2222 22 =−+−+⇒    =+ −= kxkxkyx xky 2 2 212 2 21 43 124,43 8 k kxxk kxx + −=+=+ ),,( 11 ymxMP −= ),,( 22 ymxMQ −= ),,( 1212 yyxxPQ −−= ),,2( 1212 yymxxMQMP +−+=+ 0))(())(2()( 12121212 =−++−−+=⋅+ yyyyxxmxxPQMQMP 012 ≠− xx 0)(2 1212 =++−+ yykmxx 0)2(2 12 2 12 =−++−+ xxkmxx 0)243 8(243 8 2 2 2 2 2 =−++−+ k kkmk k 2 2 43 k km += 4 10041 32 <<⇒>−= mm mk )0,(mM 2OF 10 << m )4 1,0(∈m )0()1()( >−=′ xx xaxf )(xf ( )1,0 ( )+∞,1 )(xf ( )+∞,1 ( )1,0 )(xf 20 （2）令 ，解得 a=2， ∴ ，∴ ∵ 在区间 上总不是单调函数，且 ∴ 由题意假设存在实数 m，对于任意的 ， 恒成立， 所以 ，解得 ． （3）令 ，此时 ，所以 ， 由（1）知 在 上单调递增， ∴当 时 ，即 ， ∴ 对一切 成立， ∵ ， 取 ，则 即 ， ∴ ． 18、 （1）由题意 ，解得 ． （2）当 时， 在 上单调递减，在 上单调递增， 所以 ． ( 1) 2 , [1, ]( ) , ( ,3] a x b x bg x ax b x b − + ∈=  + ∈ ( ) 122 =−=′ af ( ) 32ln2 −+−= xxxf ( ) xxmxxg 222 23 −     ++= ( ) 2)4(3 2 −++=′ xmxxg ( )xg ( )3,t (0) 2.g′ = − ( ) ( )   >′ <′ 03 0 g tg [ ]2,1∈t ( ) 0<′ tg ( ) ( ) ( )   >′ <′ <′ 03 02 01 g g g 93 37 −<<− m 1−=a ( ) 3ln −+−= xxxf ( ) 21 −=f ( ) 3ln −+−= xxxf ( )+∞,1 ( )+∞∈ ,1x ( ) )1(fxf > 01ln >−+− xx 1ln −< xx ( )+∞∈ ,1x *,2 Nnn ∈≥ 2x n= 22ln 1n n≤ − ln 1 1 2 n n n −≤+ ( )( )*,24 1 2 1 2 3 2 2 2 1 1 ln 4 3ln 3 2ln Nnnnnn n n ∈≥−<−++++<++++  ( )   +≥+− < <− babbba a a 21 0 01 0 1.2 a∴ > 0 1x< < 2 ax > ( ) 0f x′ > 1 2 ax< < ( ) 0f x′ < ( )f x∴ (0,1), , .2 a +∞   4a = 4( ) 2 6f x x x ′ = + − 40, ( ) 2 6 4 2 6x f x x x ′> ∴ = + − ≥ − 6 0x y m+ + = 42 6 3x x + − = 1 2x = 4x = 1 2x = 17 4ln 2.4n = − − 22 当 时，求得 （3） 令 ， 则 ， 当 时， 在 上单调递减． 时， 从而有 时， 当 时， 在 上单调递减， ． 从而有 时， 在 上不存在“类对称点”． 当 时， 在 上是增函数，故 是一个类对称点的横坐标． 20、（1） 函数 在 上是增函数， 对任意划分 ， ， 取常数 ，则和式 （ ）恒成立， 所以函数 在 上是有界变差函数. 4x = 4ln 4 20.n = − 2 0 0 0 0 0 0 4( ) (2 6)( ) 6 4lny g x x x x x x xx = = + − − + − + ( ) ( )00 2 00 0 0 2 ln46642ln46)()()( xxxxxxxxxxgxfx +−−−⋅      −+−+−=−= πϕ 0( ) 0.xϕ = 0 0 0 0 0 0 0 4 4 2 2 2( ) 2 6 (2 6) 2( )(1 ) ( )( )x x x x x x x xx x x x x x ϕ′ = + − − + − = − − = − − 0 2x < xϕ 0 0 2( , )x x 0 0 2( , )x x x ∴ ∈ 0( ) ( ) 0.x xϕ ϕ< = 0 0 2( , )x x x ∈ 0 4( ) 0.x x x <− 0 2x > xϕ 0 0 2( , )xx x∴ 0 0 2( , )xx ∈ 0( ) ( ) 0.x xϕ ϕ> = 0 0 2( , )x xx ∈ 0 4( ) 0.x x x <− ∴ (0, 2) ( 2, )+∞ 0 2x = 22( ) ( 2)x xx ϕ′ = − ( )xϕ∴ (0, )+∞ 0 ( ) 0.x x x ϕ >− 2x =  2)( xxf = ]1,0[ ∴ T 1)0()1()()()()()()( 101 1 1 =−=−++−=− − = −∑ ffxfxfxfxfxfxf nn n i ii  1≥M Mxfxf n i ii ≤−∑ = − 1 1)()( ni ,,2,1 = 2)( xxf = ]1,0[ 23 （2）不妨设函数 是 上的单调增加， 对任意划分 ， ， 一定存在一个常数 ，使 ，故 . （3） 对任意划分 ， ， 取常数 ， 由有界变差函数定义知 . 21、（1）令 ，得 ， ．…………………………………………① 令 得 ． ．……………………………………………② 由①、②，得 ． 为单调函数， ． （2）由（1）得 ， ， ， ， ． 又 ． ． 又 ， ． ． ． )(xf ],[ ba  T )()()()()()()()( 101 1 1 afbfxfxfxfxfxfxf nn n i ii −=−++−=− − = −∑  ∴ 0>M Mafbf ≤− )()( ],[ baBVf ∈  T )()()( 1 1 1 1 abkxxkxfxf n i ii n i ii −=−≤− ∑∑ = − = − )( abkM −= ∴ ],[ baBVf ∈ 1 2 0x x= = 0(0) ( ) 2 (0)f f x f= + 0( ) (0)f x f∴ = − 1 21, 0x x= = 0 0( ) ( ) (1) (0)f x f x f f= + + (1) (0)f f∴ = − ( ) ( )10 fxf = ( )f x 0 1x∴ = 1 2 1 2 1 2( ) ( ) ( ) (1) ( ) ( ) 1f x x f x f x f f x f x+ = + + = + + ( 1) ( ) (1) 1 ( ) 2f n f n f f n+ = + + = + (1) 1f = ( ) 2 1( )f n n n N ∗∴ = − ∈ 1 2 1na n ∴ = − 1 1 1 1(1) ( ) ( ) ( ) (1)2 2 2 2f f f f f= + = + + 1 1 1( ) 0, ( ) 1 12 2f b f∴ = = + = 1 1 1 1 1 1 1 1 1 1 1( ) ( ) ( ) ( ) (1) 2 ( ) 12 2 2 2 2 2n n n n n nf f f f f f+ + + + + = + = + + = + 1 1 1 12 2 ( ) 2 ( ) 12 2n nn nb f f b+ + ∴ = + = + = 11( )2 n nb −∴ = 1 1 1 1 1 1 1 1 1 1 1(1 ) (1 )1 3 3 5 (2 1) (2 1) 2 3 3 5 2 1 2 1 2 2 1nS n n n n n = + + + = − + − + + − = −× × − × + − + +  0 1 1 2 1 3 2 1 1 1[1 ( ) ]1 1 1 1 1 1 1 1 1 2 12 4( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [1 ( ) ]12 2 2 2 2 2 2 2 2 3 41 4 n n n n n nT − − − = + + + = + + + = = − −  24 ． ， ． ． 22、(1)因为点 的坐标为 , 的坐标为 , 所以点 的坐标为 ,则 故 的关系为 (2)设切点为 ,则 得 ,所以 解不等式 得 . . 的取值范围是 (3) 由 得 ,即 ,故 , 所 以 数 列 是 以 2 为 公 比 , 首 项 为 的 等 比 数 列 , 即 解得 , 数列 的通项公式为 . 23、（1） ，则 ， 得 ，即 ， ∴数列 是首项为 2、公差为 1 的等差数列，∴ ，即 （2） ，∴函数 在点 N*）处的切线方程为： 4 2 1 2 1 2 1 1(1 ) [1 ( ) ] [( ) ]3 3 2 1 3 4 3 4 2 1 n n n nS T n n ∴ − = − − − = −+ + 1 1 1 04 (3 1) 3 3 3 3 1 2 1n n n n n n n n n nC C C C n n− −= + = + + + + ≥ + > +  4 2 1 1[( ) ] 03 3 4 2 1 n n nS T n ∴ − = − <+ 4 3 n nS T∴ < nQ 2( , )n na a 1nQ + 2 1( , )n+1 na a + 1nP + 1( ,4 )n+1 na a + 2 14 ,n na a+ = 1n na a+ 与 2 1 1 .4n na a+ = 2( , )t t / 2y x= 2 4t = 2.t = 2 1 2, 2 a a <  > 12 2 2a< < 2 2 2 4 3 2 1 1 1 1 1 1( )4 4 4 64a a a a= = = 12 2 2,a< < ∴ 3 1 1.4 a< < 3a 1( ,1).4 2 1 1 4n na a+ = 2 1 1lg lg( )4n na a+ = 1 1lg 2lg lg 4n na a+ = + 1 1 1lg lg 2(lg lg )4 4n na a+ + = + 1 1 1 3lg lg lg3 lg lg 04 4 4a + = + = ≠ 1{lg lg }4na + 3lg 4 11 21 3 3lg lg 2 lg lg( ) ,4 4 4 nn na −−+ = = 123lg lg( ) ,4 4 nna −= 1234( )4 n na −= { }na 1234( )4 n na −=  ( ) ( 0)1 xf x xx = >+ 1 ( ) 1 n n n n aa f a a+ = = + 111 1 += + nn aa 111 1 =− + nn aa }1{ na 1 1 n na = + 1 1 += nan 2 1[ ( )] (1 )f x x ′ = + ( )f x ( , ( ))(n f n n∈ 25 ，令 ，得 ． ，仅当 时取得最小值， 只需 ，解得 ，故 的取值范围为 ． （3） ，故 ， 又 ，故 ，则 ，即 ． ∴ = ． 又 ， 故 ． 24、(1)因为对任意正整数 ， 总成立, 令 ，得 ,则 令 ，得 (1) , 从而 (2), (2)－(1)得 , 综上得 ,所以数列 是等比数列… （2）正整数 成等差数列，则 ,所以 , 则 ①当 时， ． ②当 时， ． ③当 时， ． （3）正整数 成等比数列，则 ,则 , 所以 ， ． ①当 ,即 时， ． ②当 ,即 时， ． ,n m m n m m nS S q S+ = + 1n m= = 2 1 1S S qS= + 2 1a qa= 1m = 1 1n nS S qS+ = + 2 1 1n nS S qS+ += + 2 1n na qa+ += ( 1)n ≥ 1n na qa+ = ( 1)n ≥ { }na , ,m k h 2m h k+ = 2 2 2 21 ( ) 22m h m h k+ > + = 2 2 2 22 1 1 1 m h m m m h h h k m h m h m ha a a q a q a q− − + − −⋅ = = 1q = 2 2 1 m h k k m h ka a a a⋅ = = 1q > 2 2 22 2 2 2 1 2 2 1 1 1( )m h k m h m h k k k k k k m h ka a a q a q a q a+ − − − −⋅ = > = = 0 1q< < 2 2 22 2 2 2 1 2 2 1 1 1( )m h k m h m h k k k k k k m h ka a a q a q a q a+ − − − −⋅ = < = = , ,m k h 2m h k⋅ = 1 1 1 22m h mh k + > = 1 1 1 1 1 1 1 1 1 121 1 2 1 1 1 1( ) ( ) ( )m hm h m h m h m h m h m h aa a a q a q a q q q + − − +− −⋅ = = = 2 2 2 1( )k k k aa q q = 1a q= 1 1a q = 1 1 2 m h k m h ka a a⋅ = 2 2 k kq a= = 1a q> 1 1a q > 1 1 1 1 2 2 21 1( ) ( )m h m h k m h a aa a q qq q +⋅ = > 2 k ka= 2 1 ( )1 (1 ) ny x nn n − = −+ + 0=x 2 2 2 )1()1(1 n n n n n nbn +=+−+= 2 2 2 2 ( 1) ( )2 4 n n n b n n na a λ λ λλ λ∴ + = + + = + + − 5=n 5.525.4 <−< λ 911 −<<− λ λ )9,11( −− 2( ) ( )(1 ) (1 )g x f x x x x= + = + )1()(1 nnnn cccgc +==+  02 1 1 >=c 0>nc nnnnn ccccc +−=+= + 1 11 )1( 11 1 1 11 1 1 + −=+ nnn ccc 1 2 1 2 2 3 1 1 1 1 1 1 1 1 1 1( ) ( ) ( )1 1 1 n n nc c c c c c c c c + + + + = − + − + + −+ + +  21211 111 <−=− ++ nn ccc 7 4 3 2 4 31 1 2 11 1 1 1 1 1 1 1 1 1 1 1 2121 += + + + =+++≥++++++ ccccc n  121 26 >= 21 1 1 1 1 11 21 <++++++< nccc  26 ③当 ,即 时， ． 25、（1）由题意可知， ． 令 则 ，又 ． 则数列 是首项为 ，公比为 的等比数列， 　 ，故 ， ，故 ． 　　 ． （2）用反证法证明： 假设数列 存在三项 按某种顺序成等差数列， 由于数列 是首项为 ，公比为 的等比数列，于是有 ，则只有可能有 成立- 则 ． 两边同乘 得 ． 由于 ，所以上式左边为偶数，右边为奇数，故上式不可能成立，导致矛盾． 故数列 中任意三项不可能成等差数列． 26、(1) ，依题意， ，即 . 当 时， ，解得 或 （舍去）. 当 时， 由 ， ∵ ，∴ ，则 ， ∴ 是首项为 2，公差为 2 的等差数列，故 . 另法：易得 ，猜想 ，再用数学归纳法证明(略). (2) 证法一：∵ ， 1a q< 1 1a q < 1 1 1 1 2 2 21 1( ) ( )m h m h k m h a aa a q qq q +⋅ = < 2 k ka= 2 2 1 21 (1 )3n na a+− = − 21n nc a= − }{ nc 1 3 4c = 2 3 13 2 4 3 n nc − =    1 2 1 23 2 3 21 ( ) 14 3 4 3 n n n na a − −  − = ⇒ = −    1 13 2( 1) 1 ( )4 3 n n na − −= − − { }nb , ,r s tb b b ( )r s t< < { }nb 1 4 2 3 r s tb b b> > r s t< < { }nb nn cc 3 2 1 =+ 2 1 1 31 4c a= − = 0,2 1 11 <⋅= +nn aaa 122 1 )3 2(4 1 − + ×=−= n nnn aab trs bbb +=2 111 )3 2(4 1)3 2(4 1)3 2(4 12 −−− ×+×=×× trs 11 32 −− ⋅ tr rtrtrsst −−−− +=×× 23232 1 1( ) 2 4f x x ′ = + 2 1 1( ) 2 4 n n n n S f aa a ′= = + ( 2) 4 n n n a aS += 1n = 1 1 1 1 ( 2) 4 a aa S += = 1 2a = 1 0a = 2n ≥ 1 1 1 ( 2) ( 2) 4 4 n n n n n n n a a a aa S S − − − + += − = − 2 2 1 12( )n n n na a a a− −⇒ − = + 0na > 1 0n na a −+ ≠ 1 2n na a −− = { }na 2na n= 1 2 32, 4, 6a a a= = = 2na n= 3 3 2 2 1 1 1 1 1 (2 ) 8 8 ( 1) 8( 1) ( 1)na n n n n n n n n = = < =⋅ − − + 1 1 1[ ]( 2)16 ( 1) ( 1) nn n n n = − ≥− + 27 ∴当 时， . 当 时，不等式左边 显然成立. 证法二：∵ ，∴ . ∴ . ∴当 时， . 当 时，不等式左边 显然成立. (3) 由 ，得 ， 设 ，则不等式等价于 . ， ∵ ，∴ ，数列 单调递增. 假设存在这样的实数 ，使得不等式 对一切 都成立，则 ① 当 为奇数时，得 ； ② 当 为偶数时，得 ，即 . 综上， ，由 是非零整数，知存在 满足条件． 2n ≥ 3 3 3 3 3 3 3 3 1 2 3 1 1 1 1 1 1 1 1 2 4 6 (2 )na a a a n + + + + = + + + +  3 1 1 1 1 1 1 1 1[( ) ( ) ]2 16 1 2 2 3 2 3 3 4 ( 1) ( 1)n n n n < + − + − + + −× × × × − + 1 1 1 1 1 1 1 5[ ]8 16 2 ( 1) 8 16 2 32n n = + − < + × =+ 1n = 3 1 1 1 5 8 32a = = < 3 2 24 ( 1) ( 4 4) ( 2) 0n n n n n n n n− − = − + = − ≥ 3 4 ( 1)n n n≥ − 3 3 3 1 1 1 1 1 1 1( )(2 ) 8 32 ( 1) 32 1na n n n n n n = = ≤ = −− − ( 2)n ≥ 2n ≥ 3 3 3 3 3 3 3 3 1 2 3 1 1 1 1 1 1 1 1 2 4 6 (2 )na a a a n + + + + = + + + +  3 1 1 1 1 1 1 1 1 1 1 1 1 5[(1 ) ( ) ( )] (1 )2 32 2 2 3 1 8 32 8 32 32n n n ≤ + − + − + + − = + − < + =− 1n = 3 1 1 1 5 8 32a = = < 2na n= 11cos cos( 1) ( 1)2 nna n π π ++ = + = − 1 2 1 1 1 1(1 )(1 ) (1 ) 1 n n n b aa a a = − − ⋅ ⋅ − + 1( 1)n nbλ+− < 1 1 1 1 2 1 2 2 1 (2 1)(2 3)1 1 2 31 1 2 2 nn n n n ab n n b n nna na + + + + + += = =    + +− +− +    +   2 2 4 8 4 1 4 8 3 n n n n + += > + + 0nb > 1n nb b+ > { }nb λ 1( 1)n nbλ+− < *n∈N n min 1 2 3( ) 3nb bλ < = = n min 2 8 5( ) 15nb bλ− < = = 8 5 15 λ > − 8 5 2 3( , )15 3 λ ∈ − λ 1λ = ±