2014高考压轴题带电粒子在复合场中运动含答案解析 9页

‎1.如图，在xOy平面内，MN和x轴之间有平行于y轴的匀强电场和垂直于xOy平面的匀强磁场，y轴上离坐标原点4L的A点处有一电子枪，可以沿+x方向射出速度为v0的电子（质量为m，电荷量为e）.如果电场和磁场同时存在，电子将做匀速直线运动.如果撤去电场，只保留磁场，电子将从x轴上距坐标原点3L的C点离开磁场.不计重力的影响，求：‎ ‎（1）磁感应强度B和电场强度E的大小和方向；‎ ‎（2）如果撤去磁场，只保留电场，电子将从D点（图中未标出）离开电场，求D点的坐标；‎ ‎（3）电子通过D点时的动能.‎ ‎1、:（1）只有磁场时，电子运动轨迹如图1所示 （1分）‎ 洛伦兹力提供向心力Bev0=m （1分）‎ 由几何关系R2=(3L)2+（4L-R）2 （2分）‎ 求出B=，垂直纸面向里. （1分）‎ 电子做匀速直线运动Ee=Bev0 （1分）‎ 求出E=沿y轴负方向 （1分）‎ ‎（2）只有电场时，电子从MN上的D点离开电场，如图2所示（1分）‎ 设D点横坐标为x x=v0t （2分）‎ ‎2L= （2分）‎ 求出D点的横坐标为x=≈3.5L （1分）‎ 纵坐标为y=6L. （1分）‎ ‎（3）从A点到D点，由动能定理Ee·2L=EkD-mv02 （2分）‎ 求出EkD=mv02. 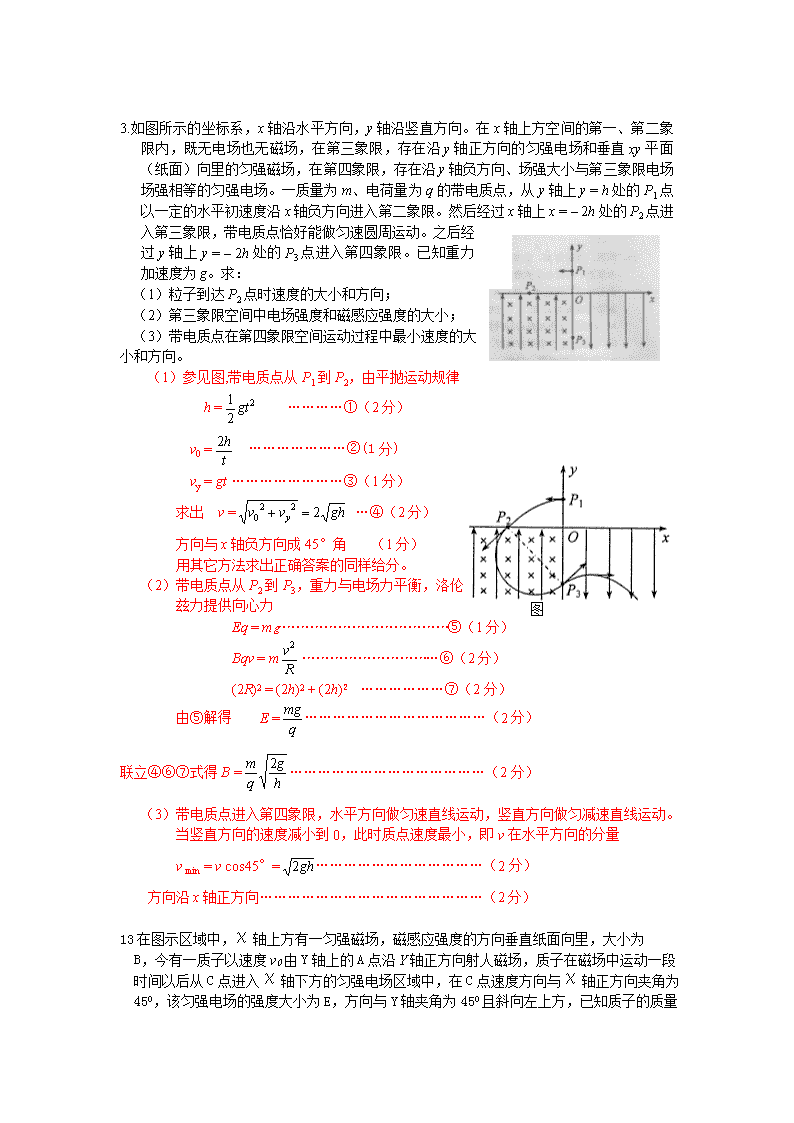‎ ‎3.如图所示的坐标系，x轴沿水平方向，y轴沿竖直方向。在x轴上方空间的第一、第二象限内，既无电场也无磁场，在第三象限，存在沿y轴正方向的匀强电场和垂直xy平面（纸面）向里的匀强磁场，在第四象限，存在沿y轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为m、电荷量为q的带电质点，从y轴上y = h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x = – 2h处的P2点进入第三象限，带电质点恰好能做匀速圆周运动。之后经过y轴上y = – 2h处的P3点进入第四象限。已知重力加速度为g。求：‎ ‎（1）粒子到达P2点时速度的大小和方向；‎ ‎（2）第三象限空间中电场强度和磁感应强度的大小；‎ ‎（3）带电质点在第四象限空间运动过程中最小速度的大小和方向。‎ ‎（1）参见图,带电质点从P1到P2，由平抛运动规律 ‎ h = …………①（2分）‎ 图 ‎ v0 = …………………②(1分)‎ ‎ vy = gt ……………………③（1分）‎ ‎ 求出 v = …④（2分）‎ ‎ 方向与x轴负方向成45°角 （1分）‎ 用其它方法求出正确答案的同样给分。‎ ‎ （2）带电质点从P2到P3，重力与电场力平衡，洛伦兹力提供向心力 ‎ Eq = mg………………………………⑤（1分）‎ ‎ Bqv = m…………………………⑥（2分）‎ ‎ (2R)2 = (2h)2 + (2h)2 ………………⑦（2分）‎ ‎ 由⑤解得 E =…………………………………（2分） ‎ 联立④⑥⑦式得B =……………………………………（2分）‎ ‎ （3）带电质点进入第四象限，水平方向做匀速直线运动，竖直方向做匀减速直线运动。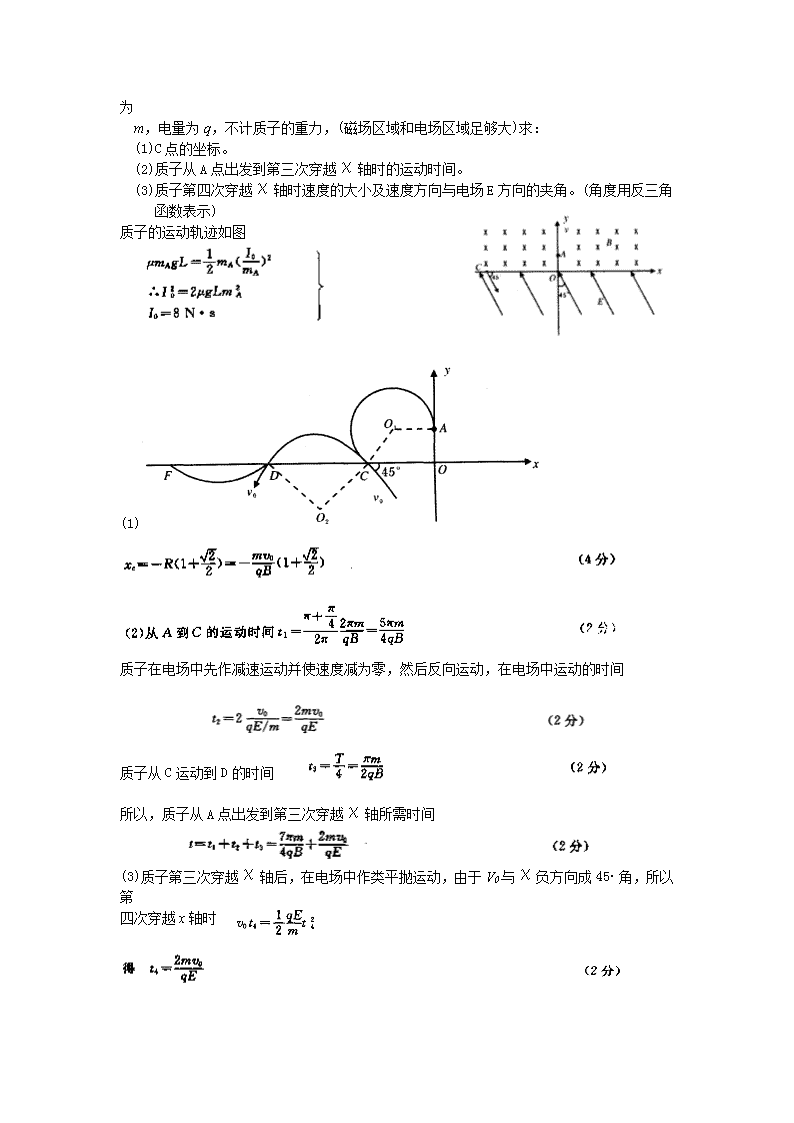当竖直方向的速度减小到0，此时质点速度最小，即v在水平方向的分量 ‎ v min = v cos45°=………………………………（2分）‎ ‎ 方向沿x轴正方向 …………………………………………（2分）‎ ‎13在图示区域中，χ轴上方有一匀强磁场，磁感应强度的方向垂直纸面向里，大小为 ‎ B，今有一质子以速度v0由Y轴上的A点沿Y轴正方向射人磁场，质子在磁场中运动一段 ‎ 时间以后从C点进入χ轴下方的匀强电场区域中，在C点速度方向与χ轴正方向夹角为 ‎ 450，该匀强电场的强度大小为E，方向与Y轴夹角为450‎ 且斜向左上方，已知质子的质量为 ‎ m，电量为q，不计质子的重力，(磁场区域和电场区域足够大)求：‎ ‎ (1)C点的坐标。‎ ‎ (2)质子从A点出发到第三次穿越χ轴时的运动时间。‎ ‎ (3)质子第四次穿越χ轴时速度的大小及速度方向与电场E方向的夹角。(角度用反三角 ‎ 函数表示)‎ 质子的运动轨迹如图 ‎(1)‎ 质子在电场中先作减速运动并使速度减为零，然后反向运动，在电场中运动的时间 质子从C运动到D的时间 所以，质子从A点出发到第三次穿越χ轴所需时间 ‎(3)质子第三次穿越χ轴后，在电场中作类平抛运动，由于V0与χ负方向成45。角，所以第 四次穿越x轴时 ‎ ‎ 所以，速度的大小为 速度方向与电场E的夹角设为θ，如图所示 ‎2．如图，在直角坐标系的第Ⅱ象限和第Ⅳ象限中的直角三角形区域内，分布着为B＝5.0×10－3T的匀强磁场，方向分别垂直纸面向外和向里．质量为m＝6.64×10－27㎏、电荷量为q＝＋3.2×10－19C的α粒子（不计α粒子重力），由静止开始经加速电压为U＝1205V的电场（图中未画出）加速后，从坐标点M（－4，）处平行于x轴向右运动，并先后通过两个匀强磁场区域．(1)请你求出α粒子在磁场中的运动半径；(2)你在图中画出α粒子从直线x＝－4到直线x＝4之间的运动轨迹，并在图中标明轨迹与直线x＝4交点的坐标；(3)求出α粒子在两个磁场区域偏转所用的总时间．‎ ‎2．解析：(1) α粒子在磁场中偏转，则牛顿第二定律得 联立解得（m）‎ O M ‎2‎ ‎－2‎ ‎2‎ ‎－4‎ ‎4‎ x/m y/m ‎－2‎ v B B ‎（4，）‎ ‎(2)由几何关系可得，α粒子恰好垂直穿过分界线，故正确图象为 ‎(3)带电粒子在磁场中的运动周期 α粒子在两个磁场中分别偏转的弧度为，运动总时间 ‎（s）‎ ‎1．如图所示，在x轴上方有匀强电场，场强为E；在x轴下方有匀强磁场，磁感应强度为B，方向如图，在x轴上有一点M，离O点距离为L．现有一带电量为十q的粒子，使其从静止开始释放后能经过M点．如果把此粒子放在y轴上，其坐标应满足什么关系？（重力忽略不计）‎ 解析：由于此带电粒子是从静止开始释放的，要能经过M点，其起始位置只能在匀强电场区域．物理过程是：静止电荷位于匀强电场区域的y轴上，受电场力作用而加速，以速度v进入磁场，在磁场中受洛仑兹力作用作匀速圆周运动，向x轴偏转．回转半周期过x轴重新进入电场，在电场中经减速、加速后仍以原速率从距O点2R处再次超过x轴，在磁场回转半周后又从距O点4R处飞越x轴如图所示（图中电场与磁场均未画出）故有L＝2R，L＝2×2R，L＝3×2R 即 R＝L/2n，（n=1、2、3……） 设粒子静止于y轴正半轴上，和原点距离为h，由能量守恒得mv2／2=qEh 对粒子在磁场中只受洛仑兹力作用而作匀速圆周运动有：R＝mv／qB 解①②③式得：h＝B2qL2／8n2mE （n＝l、2、3……）‎ ‎5．.如图所示，在坐标系Oxy的第一象限中存在沿y轴正方向的匀强电场，场强大小为E。在其他象限中存在匀强磁场，磁场方向垂直纸面向里。A是y轴上的一点，它到坐标原点O的距离为h；C是x轴上的一点，到O的距离为l。一质量为m、电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域，继而同过C点进入磁场区域，并在此通过A点，此时速度与y轴正方向成锐角。不计重力作用。试求：‎ ‎（1）粒子经过C点是速度的大小和方向；‎ ‎（2）磁感应强度的大小B。‎ ‎．解：（1）以a表示粒子在电场作用下的加速度，有qE=ma 加速度沿y轴负方向。设粒子从A点进入电场时的初速度为v0，由A点运动到C点经历的时间为t，则有 由式得 ‎ 设粒子从C点进入磁场时的速度为v，v垂直于x轴的分量 ‎ 得 ‎ 设粒子经过C点时的速度方向与x轴夹角为，则有 得 ‎ ‎（2）粒子从C点进入磁场后在磁场中做速率为v的圆周运动。‎ 若圆周的半径为R，则有 ‎ 设圆心为P，则PC必与过C点的速度垂直，且有。 ‎ 用表示与y轴的夹角，由几何关系得 解得 ‎ 得 。‎ P ‎. . . . .‎ ‎. . . . .‎ ‎. . . . .‎ ‎. . . . .‎ ‎10、如图所示的区域中，第二象限为垂直纸面向外的匀强磁场，磁感应强度为B，第一、第四象限是一个电场强度大小未知的匀强电场，其方向如图。一个质量为m，电荷量为+q的带电粒子从P孔以初速度v0沿垂直于磁场方向进入匀强磁场中，初速度方向与边界线的夹角θ=30°，粒子恰好从y轴上的C孔垂直于匀强电场射入匀强电场，经过x轴的Q点，已知OQ=OP，不计粒子的重力，求：‎ ‎ （1）粒子从P运动到C所用的时间t；‎ ‎ （2）电场强度E的大小；‎ ‎ （3）粒子到达Q点的动能Ek。‎ 答案： （1）带电粒子在电磁场运动的轨迹如图所示，由图可知，带电粒子在磁场中做匀速圆周 P ‎. . . . .‎ ‎. . . . .‎ ‎. . . . .‎ ‎. . . . .‎ 运动的轨迹为半个圆周由 得： ‎ 又T= ‎ 得带电粒子在磁场中运动的时间： ‎ ‎ （2）带电粒子在电场中做类平抛运动，初速度垂直于电场沿CF方向，过Q点作直线CF的垂线交CF于D，则由几何知识可知，CPO≌CQO≌CDQ，由图可知：CP= ‎ 带电粒子从C运动到Q沿电场方向的位移为 ‎ ‎ 带电粒子从C运动到Q沿初速度方向的位移为 ‎ 由类平抛运动规律得： ‎ 联立以上各式解得： （3）由动能定理得： ‎ 联立以上各式解得： ‎ ‎12、在图所示的坐标系中，轴水平，轴垂直，轴上方空间只存在重力场，第Ⅲ象限存在沿轴正方向的匀强电场和垂直平面向里的匀强磁场，在第Ⅳ象限由沿轴负方向的匀强电场，场强大小与第Ⅲ象限存在的电场的场强大小相等。一质量为，带电荷量大小为的质点，从轴上处的点以一定的水平速度沿轴负方向抛出，它经过处的点进入第Ⅲ象限，恰好做匀速圆周运动，又经过轴上方的点进入第Ⅳ象限，试求：‎ ‎（1）质点到达点时速度的大小和方向；‎ ‎（2）第Ⅲ象限中匀强电场的电场强度和匀强磁场的磁感应强度的大小；‎ ‎（3）质点进入第Ⅳ象限且速度减为零时的位置坐标 解析、（1）质点在第Ⅱ象限中做平抛运动，设初速度为，由 ‎ ① ② ‎ 解得平抛的初速度 在点，速度的竖直分量 ，其方向与轴负向夹角 ‎ ‎（2）带电粒子进入第Ⅲ象限做匀速圆周运动，必有 ③ ‎ ‎ 又恰能过负处，故为圆的直径，转动半径 ④ 又由 ⑤ 可解得 ‎ ‎（3）带电粒以大小为，方向与轴正向夹角进入第Ⅳ象限，所受电场力与重力的合力为，方向与过点的速度方向相反，故带电粒做匀减速直线运动，设其加速度大小为，则：‎ ‎ ⑥ ‎ ‎ 此得出速度减为0时的位置坐标是 ‎× × × × × × ×‎ ‎× × × × × × ×·‎ ‎× × × × × × ×‎ ‎× × × × × × ×‎ ‎× × × × × × ×‎ O ‎450‎ ‎(3L,L)‎ P A1‎ x y ‎17.(20分)如图所示,在xoy 坐标平面的第一象限内有一沿y 轴正方向的匀强电场,在第四象限内有一垂直于平面向内的匀强磁场,现有一质量为m 带电量为q的负粒子(重力不计)从电场中坐标为(3L,L)的P点与x轴负方向相同的速度射入，从O点与y轴正方向成夹角射出,求:‎ (1) 粒子在O点的速度大小.‎ (2) 匀强电场的场强E.‎ (3) 粒子从P点运动到O点所用的时间.‎ 解:(1)粒子运动轨迹如图所示,设粒子在P点时速度大小为,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为,方向与x轴正方向成450.可得 ‎ （1分）‎ y O ‎450‎ ‎(3L,L)‎ P x Q v v ‎(2)Q到P过程,由动能定理得 （3分） ‎ ‎ 即 （1分）‎ ‎(3)在Q点时, （2分）‎ 由P到Q过程中,‎ 竖直方向上有: （1分） （2分）‎ 水平方向有: （1分） 则OQ=3L-2L=L （1分）‎ 得粒子在OQ段圆周运动的半径 （2分）‎ Q到O的时间: （2分）‎ 粒子从P到O点所用的时间:t=t1+t2= （2分）‎