天津高考数学真题附答案解析 14页

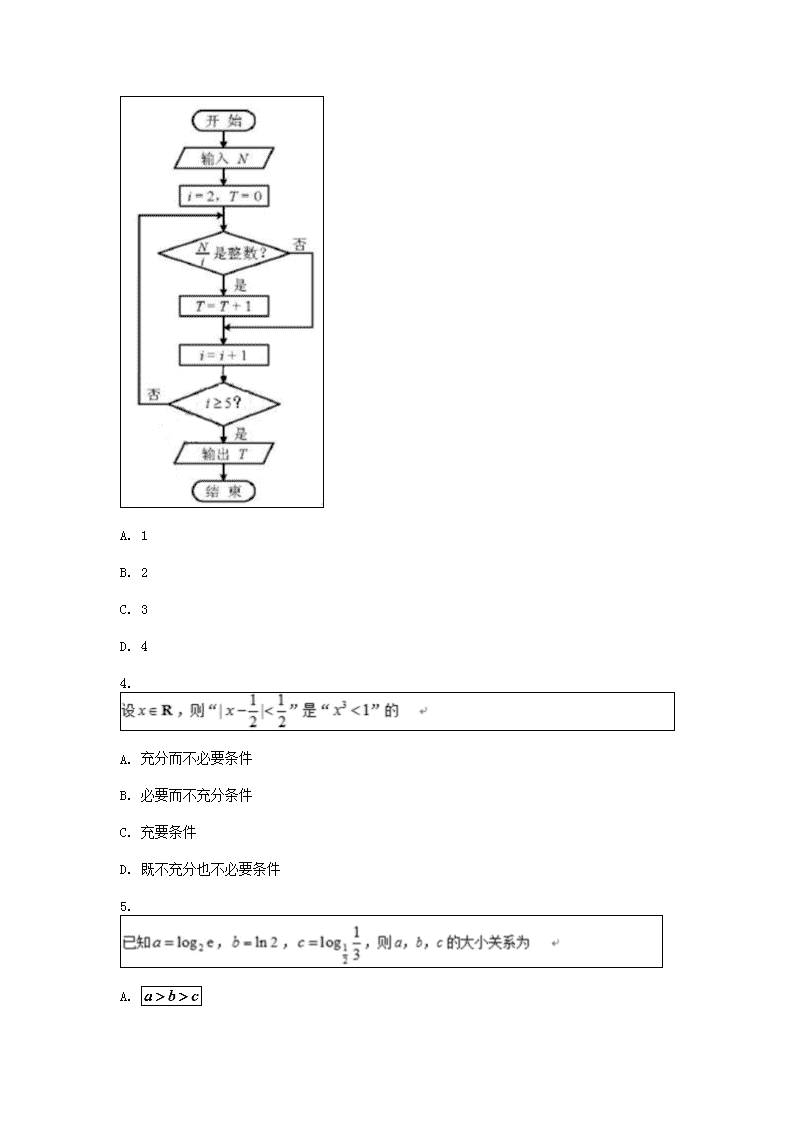
‎2018年天津高考数学真题（附答案解析）‎ ‎1.选择题(每小题5分，满分40分)：在每小题给出的四个选项中，只有一项是符合题目要求的.‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎2. ‎ A. 6‎ B. 19‎ C. 21‎ D. 45‎ ‎3.阅读如图的程序框图，运行相应的程序，若输入N的值为20，则输出T的值为 A. 1‎ B. 2‎ C. 3‎ D. 4‎ ‎4. ‎ A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎5. ‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎6. ‎ ‎7. ‎ A. A B. B C. C D. D ‎8. ‎ A. A B. B C. C D. D 填空题 （本大题共6小题，每小题____分，共____分。） ‎ ‎9.. 填空题：本大题共6小题，每小题5分，共30分。‎ ‎10. ‎ ‎11. 已知正方体的棱长为1，除面外，该正方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥的体积为____.‎ ‎12.已知圆的圆心为C，直线(为参数)与该圆相交于A，B两点，则的面积为____.‎ ‎13.已知，且，则的最小值为____.‎ ‎14.已知，函数若关于的方程恰有2个互异的实数解，则的取值范围是____.‎ 简答题（综合题） （本大题共6小题，每小题____分，共____分。） ‎ ‎15..解答题：本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤.‎ ‎（本小题满分13分）‎ 在中，内角A，B，C所对的边分别为a，b，c.已知.‎ ‎（I）求角B的大小；‎ ‎（II）设a=2，c=3，求b和的值.‎ ‎16. (本小题满分13分)‎ 已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16. 现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查.‎ ‎（I）应从甲、乙、丙三个部门的员工中分别抽取多少人？‎ ‎（II）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查.‎ ‎（i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；‎ ‎（ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.‎ ‎17.(本小题满分13分)‎ 如图，且AD=2BC，,且EG=AD，且CD=2FG，，DA=DC=DG=2.‎ ‎（I）若M为CF的中点，N为EG的中点，求证：；‎ ‎（II）求二面角的正弦值；‎ ‎（III）若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长.‎ ‎18.(本小题满分13分)‎ 设是等比数列，公比大于0，其前n项和为，是等差数列. 已知，，，.‎ ‎（I）求和的通项公式；‎ ‎（II）设数列的前n项和为，‎ ‎（i）求；‎ ‎（ii）证明.‎ ‎19.(本小题满分14分)‎ 设椭圆(a>b>0)的左焦点为F，上顶点为B. 已知椭圆的离心率为，点A的坐标为，且.‎ ‎（I）求椭圆的方程；‎ ‎（II）设直线l：与椭圆在第一象限的交点为P，且l与直线AB交于点Q.‎ 若(O为原点) ，求k的值.‎ ‎20.(本小题满分14分)‎ 已知函数，，其中a>1.‎ ‎（I）求函数的单调区间；‎ ‎（II）若曲线在点处的切线与曲线在点 处的切线平行，证明；‎ ‎（III）证明当时，存在直线l，使l是曲线的切线，也是曲线的切线.‎ 答案 单选题 ‎ ‎1.  B 2.  C 3.  B 4.  A 5.  D 6.  A 7.  C 8.  A ‎ 填空题 ‎ ‎9.  ‎ ‎4-i ‎10.  ‎ ‎11.  ‎ ‎12.  ‎ ‎13.  ‎ ‎14.  ‎ ‎(4,8)‎ 简答题 ‎ ‎15.  ‎ ‎（15）本小题主要考查同角三角函数的基本关系，两角差的正弦与余弦公式，二倍角的正弦与余弦公式，以及正弦定理、余弦定理等基础知识，考查运算求解能力．满分13分．‎ ‎（Ⅰ）解：在△ABC中，由正弦定理，可得，又由，得，即，可得．又因为，可得B=．‎ ‎（Ⅱ）解：在△ABC中，由余弦定理及a=2，c=3，B=，有，故b=．‎ 由，可得．因为a=，于是sin=．‎ 所以，二面角E–BC–F的正弦值为．‎ ‎（Ⅲ）解：设线段DP的长为h（h∈［0，2］），则点P的坐标为（0，0，h），可得．‎ 易知，=（0，2，0）为平面ADGE的一个法向量，故 ‎，‎ 由题意，可得=sin60°=，解得h=∈［0，2］．‎ 所以线段的长为.‎ ‎18.  ‎ ‎（18）本小题主要考查等差数列的通项公式，等比数列的通项公式及前n项和公式等基础知识.考查等差数列求和的基本方法和运算求解能力.满分13分.‎ ‎（I）解：设等比数列的公比为q.由可得.‎ 因为，可得，故.‎ 设等差数列的公差为d，由，可得由，‎ 可得 从而 故 所以数列的通项公式为，数列的通项公式为 ‎（II）（i）由（I），有，故 ‎.‎ ‎（ii）证明：因为 ‎，‎ 所以，.‎ ‎19.  ‎ ‎（19）本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识．考查用代数方法研究圆锥曲线的性质．考查运算求解能力，以及用方程思想解决问题的能力．满分14分．‎ ‎（Ⅰ）解：设椭圆的焦距为2c，由已知知，又由a2=b2+c2，可得2a=3b．由已知可得，，，由，可得ab=6，从而a=3，b=2．‎ 所以，椭圆的方程为．‎ ‎（Ⅱ）解：设点P的坐标为（x1，y1），点Q的坐标为（x2，y2）．由已知有y1>y2>0，故．又因为，而∠OAB=，故．由，可得5y1=9y2．‎ 由方程组消去x，可得．易知直线AB的方程为x+y–2=0，由方程组 消去x，可得．由5y1=9y2，可得5（k+1）=，两边平方，整理得，解得，或．‎ 所以，k的值为 ‎20.  ‎ ‎（20）本小题主要考查导数的运算、导数的几何意义、运用导数研究指数函数与对数函数的性质等基础知识和方法.考查函数与方程思想、化归思想.考查抽象概括能力、综合分析问题和解决问题的能力.满分14分.‎ ‎（I）解：由已知，，有.‎ 令，解得x=0.‎ 由a>1，可知当x变化时，，的变化情况如下表：‎ 所以函数的单调递减区间，单调递增区间为.‎ ‎（II）证明：由，可得曲线在点处的切线斜率为.‎ 由，可得曲线在点处的切线斜率为.‎ 因为这两条切线平行，故有，即.‎ 两边取以a为底的对数，得，所以.‎ ‎（III）证明：曲线在点处的切线l1：.‎ 曲线在点处的切线l2：.‎ 要证明当时，存在直线l，使l是曲线的切线，也是曲线的切线，只需证明当时，存在，，使得l1和l2重合.‎ 即只需证明当时，方程组有解，‎ 由①得，代入②，得.   ③‎ 因此，只需证明当时，关于x1的方程③有实数解.‎ 设函数，即要证明当时，函数存在零点.‎ ‎，可知时，；时，单调递减，又 ‎，，故存在唯一的x0，且x0>0，使得，即 ‎.‎ 由此可得在上单调递增，在上单调递减. 在处取得极大值.‎ 因为，故，‎ 所以.‎ 下面证明存在实数t，使得.‎ 由（I）可得，‎ 当时，‎ 有，‎ 所以存在实数t，使得 因此，当时，存在，使得.‎ 所以，当时，存在直线l，使l是曲线的切线，也是曲线的切线.‎ ‎ ‎