桐中高考数学文科模拟试题 3页

第I卷（选择题 共50分）‎ 一、选择题（本大题有12小题，每小题5分，共60分.每小题都有四个选项，其中有且只有一个选项是正确的）‎ ‎1．已知集合M=，N=，则 开始 结束 是 是 存在零点？‎ 输入函数 输出函数 否 否 A． B． C． D．‎ ‎2．已知复数，则复数的虚部为 A． B．‎0 C． D．‎ ‎3．某程序框图如图所示，现输入如下四个函数，则可以输出的函数是 A． B． ‎ C． D．‎ ‎4．设原命题：若，则中至少有一个不小于1。则原命题与其逆命题的真假情况是：‎ A．原命题假，逆命题真 B．原命题真，逆命题假 C．原命题与逆命题均为真命题 D．原命题与逆命题均为假命题 ‎5．已知各项不为的等差数列，满足，数列是等比数列，且 ‎，则 A．4 B．‎8 C．16 D．32‎ BB A y x ‎1‎ O 第6题图 ‎6．函数的部分图像如图所示,则=‎ A． B． C． D． ‎ ‎7．已知A船在灯塔C北偏东850且A到C的距离为‎2km，B船在灯 塔C西偏北250且B到C的距离为km，则A、B两船的距离为 A． B． C． D．‎ ‎8．已知，直线与直线互相垂直，则的最小值为 A． 4 B． ‎3 ‎‎ C ．2 D ．1‎ ‎9．一个不透明圆锥体的正视图和侧视图（左视图）为两全等的正三角形，若将它倒立放在 桌面上（即圆锥体的顶点在桌面上），则该圆锥体在桌面上从垂直位置旋转到水平位置的过 程中,其在水平桌面上正投影不可能是 椭圆形区域 等腰三角形两腰与半椭圆围成的区域 等腰三角形两腰与 半圆围成的区域 圆形区域 A B D C ‎ ‎ ‎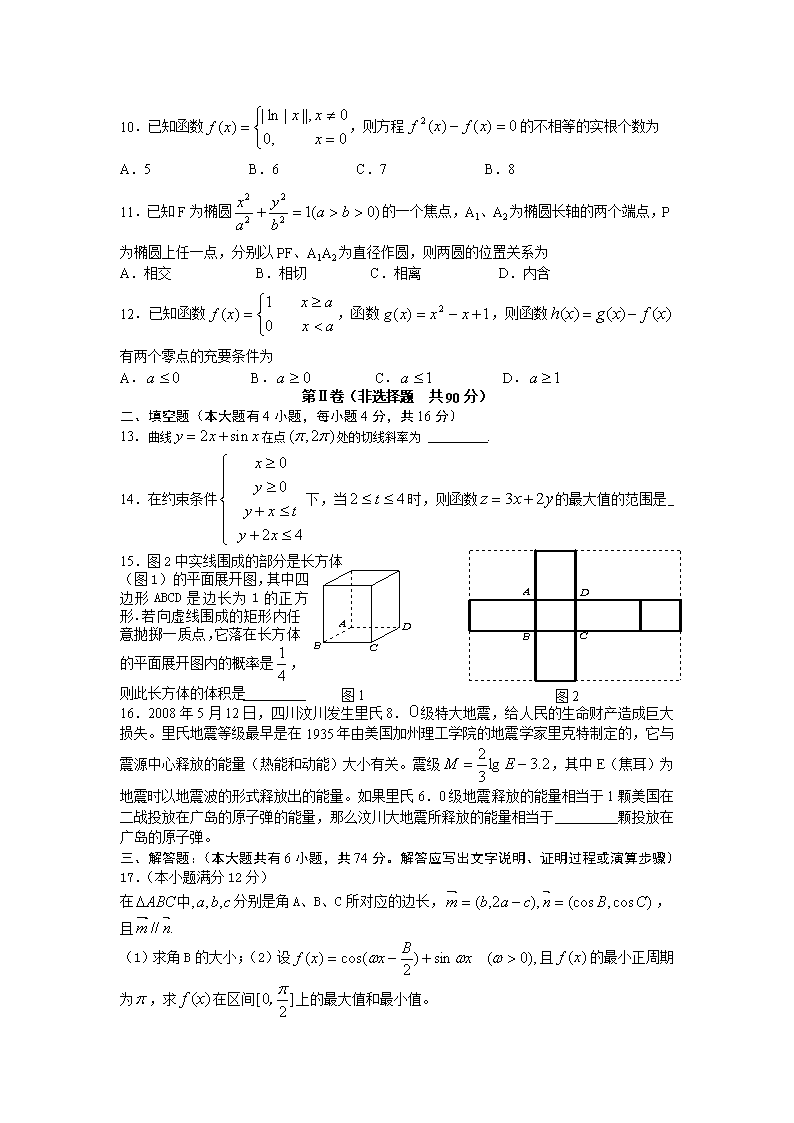10．已知函数，则方程的不相等的实根个数为 A．5 B．‎6 C．7 B．8‎ ‎11．已知F为椭圆的一个焦点，A1、A2为椭圆长轴的两个端点，P为椭圆上任一点，分别以PF、A‎1A2为直径作圆，则两圆的位置关系为 A．相交 B．相切 C．相离 D．内含 ‎12．已知函数，函数，则函数有两个零点的充要条件为 A． B． C． D．‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题（本大题有4小题，每小题4分，共16分）‎ ‎13．曲线在点处的切线斜率为 . ‎ 图2‎ 图1‎ ‎14．在约束条件下，当时，则函数的最大值的范围是 ‎ ‎15．图2中实线围成的部分是长方体（图1）的平面展开图，其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点，它落在长方体的平面展开图内的概率是，则此长方体的体积是 ‎ ‎16．‎2008年5月12日，四川汶川发生里氏8．０级特大地震，给人民的生命财产造成巨大损失。里氏地震等级最早是在1935年由美国加州理工学院的地震学家里克特制定的，它与震源中心释放的能量（热能和动能）大小有关。震级，其中E（焦耳）为地震时以地震波的形式释放出的能量。如果里氏6．0级地震释放的能量相当于1颗美国在二战投放在广岛的原子弹的能量，那么汶川大地震所释放的能量相当于 颗投放在广岛的原子弹。‎ 三、解答题：（本大题共有6小题，共74分。解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分12分）‎ 在分别是角A、B、C所对应的边长，，‎ 且 ‎（1）求角B的大小；（2）设且的最小正周期为，求在区间上的最大值和最小值。‎ ‎18．（本小题满分12分）‎ 已知圆过两点,且圆心在直线上.‎ ‎(Ⅰ)求圆的方程;‎ ‎(Ⅱ)设是直线上的动点，、是圆的两条切线，、为切点，求四边形面积的最小值.‎ ‎19．（本小题满分12分）‎ 为了了解某年级段1000名学生的百米成绩情况，随机抽取了若干名学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.‎ ‎（Ⅰ）将频率当作概率，请估计该年级段的学生中百米成绩在[16，17）内的人数；‎ ‎（Ⅱ）求调查中随机抽取了多少名学生的百米成绩；‎ ‎（Ⅲ）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.‎ ‎20．（本小题满分12分）‎ 如图1所示，在边长为的正方形中，，且，,分别交于点，将该正方形沿、折叠，使得与重合，构成如图2所示的三棱柱中 ‎（Ⅰ）求证：；‎ ‎（Ⅱ）在底边上是否存 在一点,满足平面，若存在试确定点的位置，若不存在请说明理由.‎ ‎21．（本小题满分12分） ‎ 在数列中，.‎ ‎(Ⅰ)求证：数列为等差数列；‎ ‎(Ⅱ)设数列满足，若 对一切且恒成立，求实数的取值范围.‎ ‎22．（本小题满分14分） ‎ 已知函数 ，且满足，上恒成立.‎ ‎（1）求的值；‎ ‎（2）若求解关于的不等式；‎ ‎（3）是否存在实数，使函数上有最小值－5？若存在，请求出实数的值；若不存在，请说明理由.‎