全国各地高考数学三轮复习试题汇编专题1集合与常用逻辑用语复数与算法复数与算法A卷 10页

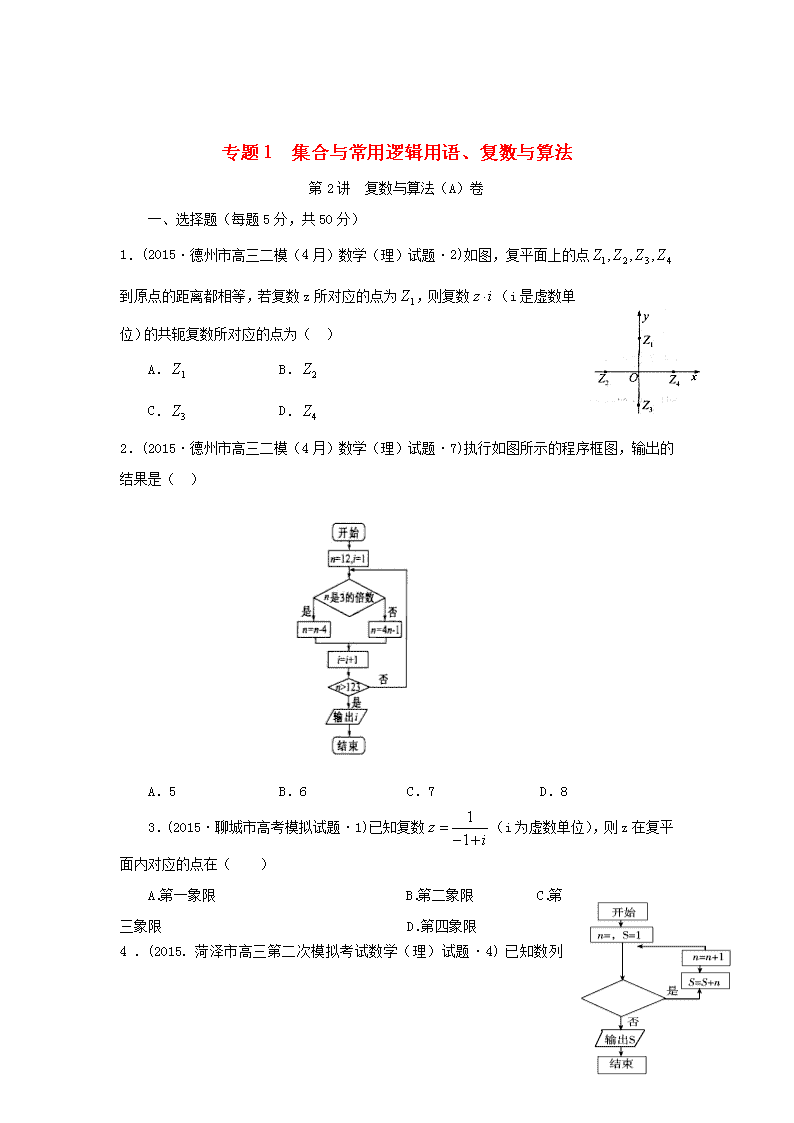
专题1 集合与常用逻辑用语、复数与算法 第2讲 复数与算法（A）卷 一、 选择题（每题5分，共50分）‎ ‎1．(2015·德州市高三二模（4月）数学（理）试题·2)如图，复平面上的点到原点的距离都相等，若复数z所对应的点为，则复数（i是虚数单位）的共轭复数所对应的点为（　）‎ A． B．‎ C． D．‎ ‎2．(2015·德州市高三二模（4月）数学（理）试题·7)执行如图所示的程序框图，输出的结果是（　）‎ A．5 B．‎6 ‎C．7 D．8‎ ‎3．(2015·聊城市高考模拟试题·1)已知复数（i为虚数单位），则z在复平面内对应的点在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎4．(2015.菏泽市高三第二次模拟考试数学（理）试题·4)已知数列 ‎，若利用如图所示的程序框图计算该数列的第10项，则判断框内的条件是（　　） ‎ A． 　B． 　　C． 　D．‎ ‎5．(2015.菏泽市高三第二次模拟考试数学（理）试题·2)已知是虚数单位，若，则的虚部为（　　） ‎ A． B． C． D．‎ ‎6. (江西省新八校2014-2015学年度第二次联考·2)已知为实数，为虚数单位，若，则（ ）‎ ‎ A. 1 B. C. D. ‎ ‎7.（2015·赣州市高三适用性考试·2）‎ ‎8．(2015·丰台区学期统一练习二·2）“a=‎0”‎是“复数(a，b∈R)为纯虚数”的（ ）‎ ‎(A) 充分不必要条件 (B) 必要不充分条件 ‎(C) 充分必要条件 (D) 既不充分也不必要条件 ‎9．（2015·山东省淄博市高三阶段性诊断考试试题·1）已知复数z满足（其中i为虚数单位），则z的共轭复数是（　　）‎ A． B． C． D． ‎ ‎10.（2015·赣州市高三适用性考试·3）‎ 二、非选择题（50分）‎ ‎11．（2015·南京市届高三年级第三次模拟考试·1）已知复数z＝－1，其中i为虚数单位，则z的模为 ．‎ ‎12．(2015·聊城市高考模拟试题·13)执行如图所示的程序框图，若输入的，则输出的T的值为_________．‎ ‎13．(2015.江西省上饶市高三第三次模拟考试·14)执行右边的程序框图,如果，输入的依次为1,2,3,4,5,5,4,3,2,1,则输出的S为 ‎ ‎14．（2015·南京市届高三年级第三次模拟考试·4）右图是一个算法流程图，则输出k的值是 ．‎ N S←40‎ 开始 k←1‎ k←k＋1‎ S≤0‎ Y 输出k 结束 S←S－2k ‎（第4题图）‎ ‎15．（2015·苏锡常镇四市高三数学调研（二模）·2）设为虚数单位，），则的值为 ‎ ‎16．(绵阳市高中2015届第三次诊断性考试·6)已知S为执行如图所示的程序框图输出的结果，则二项式的展开式中常数项的系数是 ‎ ‎17．（2015·苏锡常镇四市高三数学调研（二模）·4）根据如图所示的伪代码，若输入的值为，则输出的值为 ‎ ‎18．(2015.南通市高三第三次调研测试·5)在如图所示的算法流程图中，若输出的y的值为26，则输入的x的值为 ．‎ ‎ ‎ ‎19．(2015.南通市高三第三次调研测试·2)已知复数z=(i为虚数单位)，则z的实部为 ．‎ ‎20. ( 徐州、连云港、宿迁三市2015届高三第三次模拟·4)执行如图所示的算法流程图，则输出的值是 .‎ ‎专题1 集合与常用逻辑用语、复数与算法 第2讲 复数与算法（A）卷答案与解析 ‎1.【答案】B ‎【命题立意】本题旨在考查复数知识．‎ ‎【解析】不妨假设，则：．故选：B．‎ ‎2.【答案】B ‎【命题立意】本题旨在考查算法与流程图知识．‎ ‎【解析】程序运行如下：‎ 此时结束循环，输出结果为6．故选：B ‎3.【答案】C ‎【命题立意】本小题主要考查复数的基本运算,重点考查分母实数化的转化技巧．‎ ‎【解析】‎ ‎ ‎ ‎4.【答案】B ‎【命题立意】本题旨在考查数列的递推关系式，算法的程序框图．‎ ‎【解析】根据算法的程序框图，由于an+1=an+n，要计算该数列的第10项，由于是判断后再计算S=S+n，则当n=9时计算a10的值，则判断框内的条件是：n≤9？．‎ ‎5.【答案】A ‎【命题立意】本题旨在考查复数的概念与运算．‎ ‎【解析】由题得z====+i，则其虚部为．‎ ‎6.【答案】C ‎【命题立意】考查复数的概念、复数的运算，考查计算能力，容易题.‎ ‎【解析】，若，则，.‎ ‎7.【答案】C ‎【命题立意】本题主要考查复数的基本运算，比较基础.‎ ‎【解析】设，则，‎ ‎∵是实数，∴b-4=0，解得b=4，即，‎ 则，选C.‎ ‎8.【答案】B ‎【命题立意】考查复数的概念，充分条件与必要条件，考查运用概念解决问题的能力，容易题．‎ ‎【解析】若且，复数复数(a，b∈R)为实数；复数(a，b∈R)为纯虚数，则必有，所以“a=0”是“复数(a，b∈R)为纯虚数”的必要不充分条件．‎ ‎9.【答案】A ‎【命题立意】本题主要考查复数的运算及复数的相关概念 ‎【解析】由得，故z的共轭复数为．‎ ‎10.【答案】B ‎【命题立意】本题主要考查程序框图的识别和应用，根据条件进行模拟进行即可.‎ ‎【解析】第一次运行，A=0，i=1,A=1,i=2，‎ 第二次运行，A=3，i=3,‎ 第三次运行，A=7,i=4,‎ 第四次运行，A=15,i=5，满足条件，输出A=15，选B.‎ ‎11.【答案】 ‎【命题立意】本题旨在考查复数的运算与概念．‎ ‎【解析】由于z＝－1=－1=－1=－1+i－1=－2+i，则|z|=‎ ‎=．‎ ‎12.【答案】3‎ ‎【命题立意】本题旨在考查程序框图和算法中循环结构．‎ ‎【解析】T=2，a=4；，a=6；a=8；结束．输出的T的值为3．‎ ‎13.【答案】4 ‎ ‎【命题立意】本题重点考查了程序框图、循环结构的程序框图的执行情况等知识，属于中档题．‎ ‎【解析】结合程序框图，得初始值：；‎ 第一次循环：；‎ 第二次循环：；‎ 第三次循环：；‎ 第四次循环：；‎ 第五次循环：；‎ 第六次循环：；‎ 第七次循环：；‎ 第八次循环：；‎ 第九次循环：；‎ 第十次循环：；‎ 输出的值为4．‎ ‎14.【答案】6‎ ‎【命题立意】本题旨在考查算法流程图．‎ ‎【解析】开始时k=1，S=40，此时不满足条件S≤0；接下来有S=40－21=38，k=1+1=2，此时不满足条件S≤0；接下来有S=38－22=34，k=2+1=3，此时不满足条件S≤0；接下来有S=34－23=26，k=3+1=4，此时不满足条件S≤0；接下来有S=26－24=10，k=4+1=5，此时不满足条件S≤0；接下来有S=10－25=－22，k=5+1=6，此时满足条件S≤0，结束循环，输出k=6．‎ ‎15.【答案】‎ ‎【命题立意】本题旨在考查复数的运算，两复数相等的条件．‎ ‎【解析】由于1+2i=2i（a+bi）=－2b+2ai，则有，解得，故a+b=．‎ ‎16.【答案】-20‎ ‎【命题立意】考查程序框图与二项式定理．‎ ‎【解析】由i=0,S=1;i=1,S=-1; i=2,S=3; i=3,S=,结束．故输出．的展开式中第r+1项为：，故展开式中的常数项为．‎ ‎17.【答案】2‎ ‎【命题立意】本题旨在考查算法的伪代码及其应用．‎ ‎【解析】由算法的伪代码可得y=，而输入的x的值为－1，那么输出的y=1－（－1）=2．‎ ‎18.【答案】-4‎ ‎【命题立意】本题考查程序框图，条件结构，意在考查识图能力，容易题.‎ ‎【解析】当，解得或，由框图知，输入的x的值为.‎ ‎19.【答案】3‎ ‎【命题立意】本题考查复数的概念，意在考查对复数概念的理解能力.容易题.‎ ‎【解析】，所以z的实部为3.‎ ‎20.【答案】4‎ ‎【命题立意】本题旨在考查算法流程图．‎ ‎【解析】根据算法流程图，开始时k=1，S=0，此时满足S<12；接下来有S=0+2×1=2，k=1+1=2，此时满足S<12；接下来有S=2+2×2=6，k=2+1=3，此时满足S<12；接下来有S=6+2×3=12，k=3+1=4，此时不满足S<12，结束循环，输出k=4．‎ ‎ ‎