高考试题——数学文安徽卷 12页

‎2007年普通高等学招生全国统一考试（安徽卷）‎ 数 学（文科）‎ ‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至第2页，第Ⅱ卷第3至第4页。全卷满分150分，考试时间120分钟。‎ 考生注意事项：‎ ‎ 1.答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答 题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。‎ ‎ 2.答第Ⅰ卷时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。‎ 如需改动，用橡皮擦干净后，再选涂其他答案标号。‎ ‎3.答第Ⅱ卷时，必须用0.5毫米黑色墨水签字笔在答题卡上书写。在试题卷上作答无效。‎ ‎4.考试结束，监考员将试题卷和答题卡一并收回。‎ 参考公式：‎ 如果事件、互斥，那么 球的表面积公式 ‎ ‎ 如果事件、相互独立，那么 其中表示球的半径 ‎ 球的体积公式 ‎1+2…+n= ‎ ‎…+ 其中表示球的半径 ‎…+‎ 第Ⅰ卷（选择题共55分）‎ 一、选择题：本大题共11小题，每小题5分，共55分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎（1）若，则＝‎ ‎ （A） （B） （C） (D) ‎ ‎（2）椭圆的离心率为 ‎ （A） （B） （C） （D）‎ ‎（3）等差数列的前项和为若 ‎ （A）12 （B）10 （C）8 （D）6‎ ‎(4)下列函数中,反函数是其自身的函数为 ‎(A) (B)‎ ‎(C) (D) ‎ ‎(5)若圆的圆心到直线的距离为,则a的值为 ‎(A)-2或2 (B) (C)2或0 (D)-2或0‎ ‎(6)设均为直线,其中在平面α内，则“l⊥α”是“”的 ‎(A)充分不必要条件 (B)必要不充分条件 ‎(C)充分必要条件 (D)既不充分也不必要条件 ‎(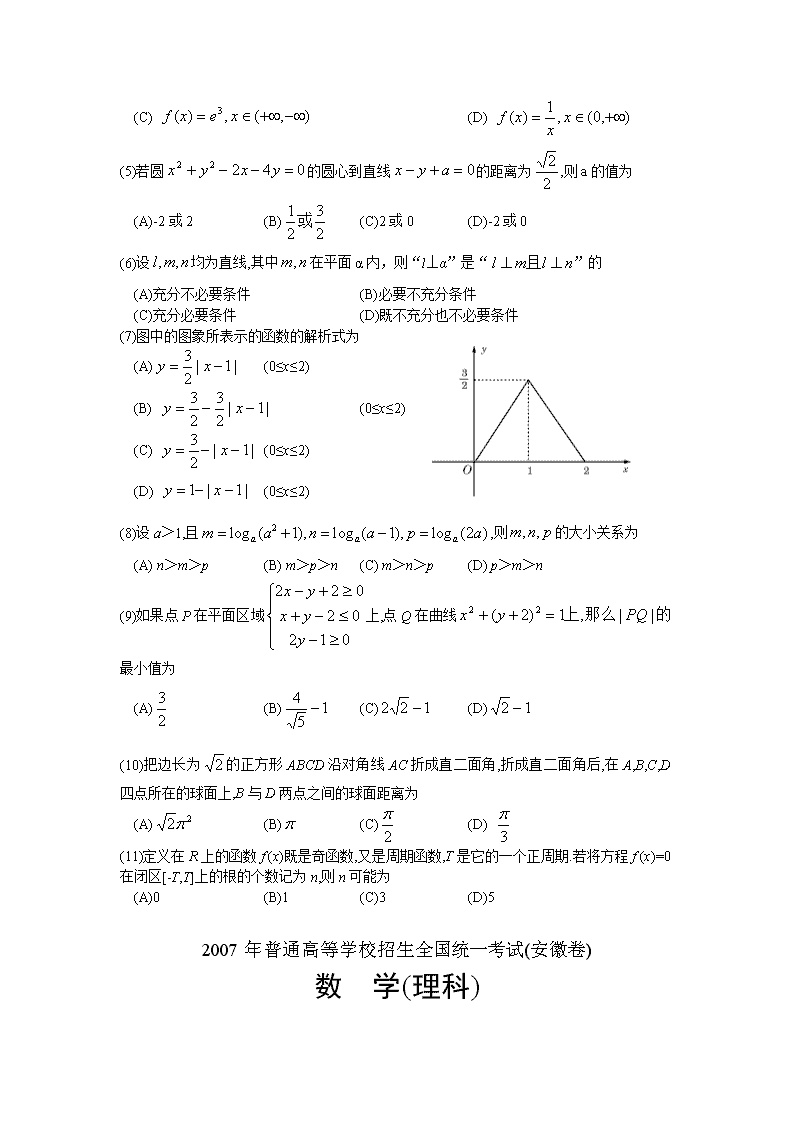7)图中的图象所表示的函数的解析式为 ‎(A) (0≤x≤2) ‎ ‎(B) (0≤x≤2)‎ ‎(C) (0≤x≤2)‎ ‎(D) (0≤x≤2)‎ ‎(8)设a＞1,且,则的大小关系为 ‎(A) n＞m＞p (B) m＞p＞n (C) m＞n＞p (D) p＞m＞n ‎(9)如果点P在平面区域上,点Q在曲线最小值为 ‎(A) (B) (C) (D)‎ ‎(10)把边长为的正方形ABCD沿对角线AC折成直二面角,折成直二面角后,在A,B,C,D四点所在的球面上,B与D两点之间的球面距离为 ‎(A) (B) (C) (D) ‎ ‎(11)定义在R上的函数f (x)既是奇函数,又是周期函数,T是它的一个正周期.若将方程f (x)=0在闭区[-T,T]上的根的个数记为n,则n可能为 ‎(A)0 (B)1 (C)3 (D)5‎ ‎2007年普通高等学校招生全国统一考试(安徽卷)‎ 数 学(理科)‎ 第Ⅱ卷(非选择题 共95分)‎ 注意事项:‎ 请用0.5毫米黑色水签字笔在答题卡上书写作答,在试题卷上书写作答无效.‎ 二、填空题:本大共4小题,每小题4分,共16分,把答案填在答题卡的相应位置.‎ ‎(12)已知,则( 的值等于 .‎ ‎(13) 在四面体O-ABC中，为BC的中点，E为AD的中点，则= （用a，b，c表示）‎ ‎(14)在正方体上任意选择两条棱,则这两条棱相互平行的概率为 .‎ ‎(15)函数的图象为C,如下结论中正确的是 (写出所有正确结论的编号).‎ ‎①图象C关于直线对称;‎ ‎②图象C关于点对称;‎ ‎③函数)内是增函数;‎ ‎④由的图象向右平移个单位长度可以得到图象C.‎ 三、解答题：本大题共6小题，共79分.解答应写出文字说明、证明过程或演算步骤.‎ ‎（16）（本小题满分10分）‎ 解不等式＞0.‎ ‎(17) （本小题满分14分）‎ 如图,在六面体中,四边形ABCD是边 ‎ 长为2的正方形,四边形是边长为1的正方 形,平面,平面ABCD, ‎ ‎(Ⅰ)求证:‎ ‎(Ⅱ)求证:平面 ‎(Ⅲ)求二面角的大小(用反三角函数值表示).‎ ‎ 第(17)题图 ‎（18）（本小题满分14分）‎ ‎　　　设F是抛物线G:x2=4y的焦点.‎ ‎　　　（Ⅰ）过点P（0，-4）作抛物线G的切线，求切线方程：‎ ‎（Ⅱ）设A、B为势物线G上异于原点的两点，且满足,延长AF、BF分别交抛物线G于点C,D，求四边形ABCD面积的最小值.‎ ‎(19)(本小题满分13分)‎ 在医学生物学试验中，经常以果蝇作为试验对象.一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.‎ ‎ (Ⅰ)求笼内恰好剩下1只果蝇的概率；‎ ‎　（Ⅱ）求笼内至少剩下5只果蝇的概率.‎ ‎(20)(本小题满分14分)‎ 设函数 ‎　　f（x）=-cos2x-4tsincos+4t2+t2-3t+4,x∈R,‎ 其中≤1，将f(x)的最小值记为g(t).‎ ‎(Ⅰ)求g(t)的表达式；‎ ‎(Ⅱ)诗论g(t)在区间（-1,1）内的单调性并求极值.‎ ‎（21）（本小题满分14分）‎ ‎　　　某国采用养老储备金制度，公民在就业的第一年就交纳养老储备金，数目为a1,以后第年交纳的数目均比上一年增加d(d>0),因此，历年所交纳的储备金数目a1,a2,…是一个公差为d的等差数列，与此同时，国家给予优惠的计息政策，不仅采用固定利率，而且计算复利，这就是说，如果固定年利率为r(r>0)，那么，在第n年末，第一年所交纳的储备金就变为n(1+r)n-1，第二年所交纳的储备金就变为a2(1+r)n-2,……，以Tn表示到第n年末所累计的储备金总额.‎ ‎　（Ⅰ）写出Tn与Tn-1（n≥2）的递推关系式；‎ ‎　（Ⅱ）求证：Tn=An+Bn，其中是一个等比数列，是一个等差数列.‎ ‎2007年普通高等学校招生全国统一考试（安徽卷）‎ 数学（文史）参考答案 一、选择题：本题考查基本知识的基本运算．每小题5分，满分55分．‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ 答案 D A C D C A B B A C D ‎（1）若，则＝，选D。‎ ‎（2）椭圆中，，∴，离心率为，选A。‎ ‎（3）等差数列的前项和为，若则=－2，，∴ ，选C。 ‎ ‎ (4)下列函数中,反函数是其自身的函数为，选D。‎ ‎ (5)若圆的圆心(1，2)到直线的距离为，∴ ，∴ a=2或0，选C。‎ ‎ (6)设均为直线,其中在平面α内，若“l⊥α”则“”，反之若“”，当m//n时，无法判断“l⊥α”，所以“l⊥α”是“”的充分不必要条件，选A。 ‎ ‎(7)图中的图象所表示的函数当0≤x≤1时，它的解析式为，当1