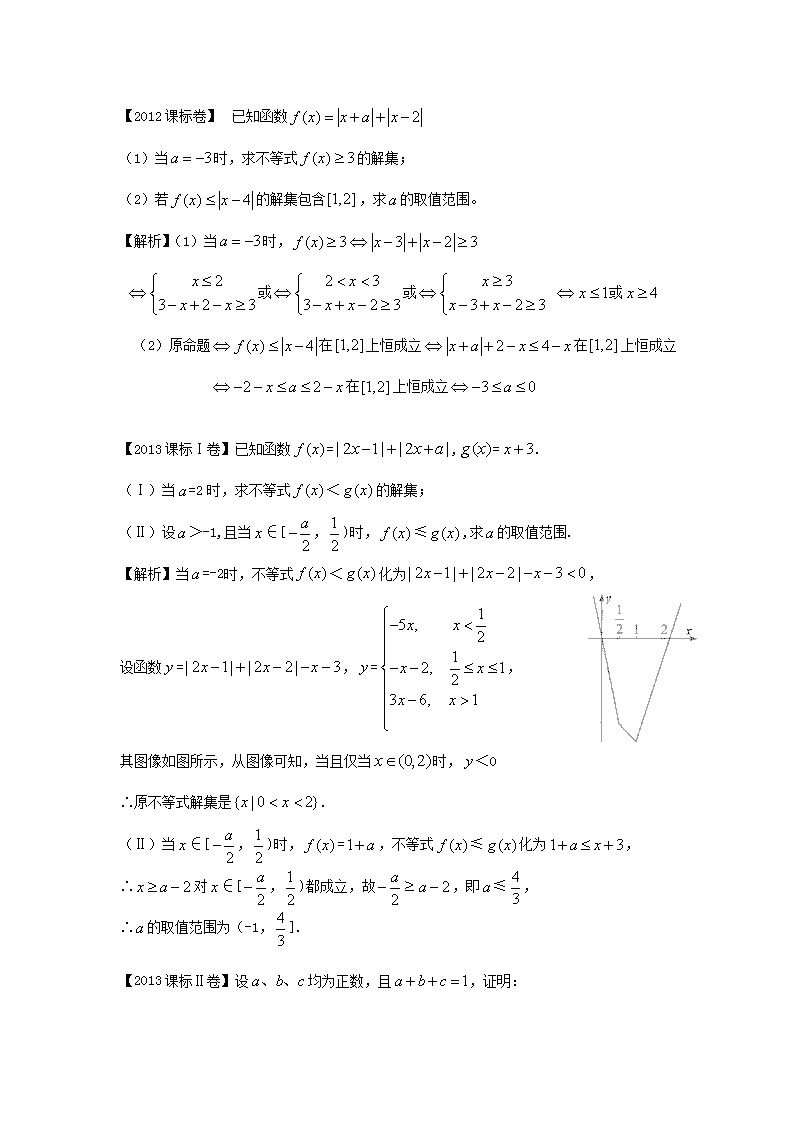不等式高考真题汇编含答案 5页

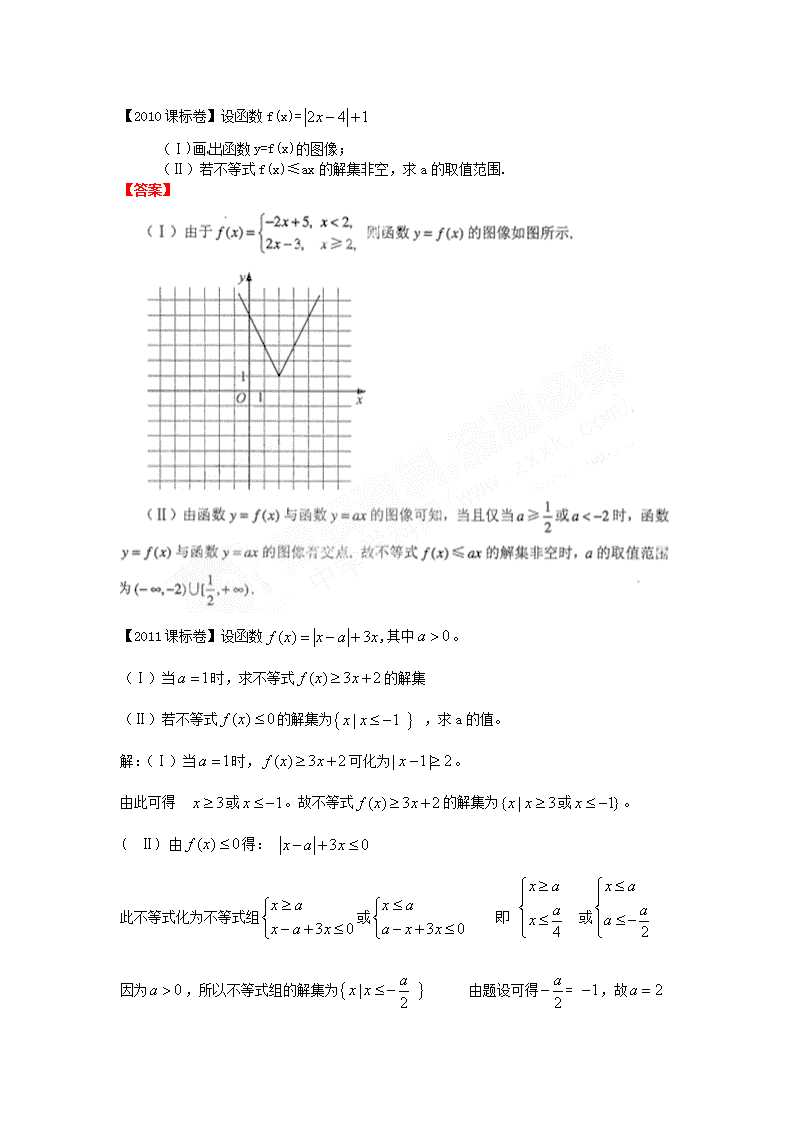
‎【2010课标卷】设函数f(x)=‎ ‎（Ⅰ)画出函数y=f(x)的图像；‎ ‎（Ⅱ）若不等式f(x)≤ax的解集非空，求a的取值范围.‎ ‎【答案】‎ ‎【2011课标卷】设函数,其中。‎ ‎（Ⅰ）当时，求不等式的解集 ‎（Ⅱ）若不等式的解集为 ，求a的值。‎ 解：（Ⅰ）当时，可化为。‎ 由此可得 或。故不等式的解集为或。‎ ‎( Ⅱ) 由得： ‎ 此不等式化为不等式组或 即 或 因为，所以不等式组的解集为 由题设可得= ，故 ‎【2012课标卷】 已知函数 ‎（1）当时，求不等式的解集；‎ ‎（2）若的解集包含，求的取值范围。‎ ‎【解析】（1）当时，‎ ‎ 或或 或 ‎ （2）原命题在上恒成立在上恒成立 在上恒成立 ‎【2013课标Ⅰ卷】已知函数=,=.‎ ‎（Ⅰ）当=2时，求不等式＜的解集；‎ ‎（Ⅱ）设＞-1,且当∈[，)时，≤,求的取值范围.‎ ‎【解析】当=-2时，不等式＜化为，‎ 设函数=，=，‎ 其图像如图所示，从图像可知，当且仅当时，＜0‎ ‎∴原不等式解集是.‎ ‎（Ⅱ）当∈[，)时，=，不等式≤化为，‎ ‎∴对∈[，)都成立，故，即≤，‎ ‎∴的取值范围为（-1，].‎ ‎【2013课标Ⅱ卷】设均为正数，且，证明：‎ ‎（Ⅰ）；（Ⅱ）‎ ‎【2014课标Ⅰ卷】若，且.‎ ‎(Ⅰ) 求的最小值；（Ⅱ）是否存在，使得？并说明理由.‎ ‎【解析】：(Ⅰ) 由，得，且当时等号成立，‎ 故，且当时等号成立，∴的最小值为. ‎ ‎（Ⅱ）由，得，又由(Ⅰ)知，二者矛盾，‎ 所以不存在，使得成立. ‎ ‎【2014课标Ⅱ卷】设函数=‎ ‎（Ⅰ）证明：2；（Ⅱ）若，求的取值范围.‎ ‎【2015课标Ⅰ卷】已知函数 .‎ ‎（I）当 时求不等式 的解集；‎ ‎（II）若 图像与x轴围成的三角形面积大于6，求a的取值范围.‎ ‎（Ⅱ）由题设可得，，‎ ‎ 所以函数的图像与轴围成的三角形的三个顶点分别为，，，所以△ABC的面积为.‎ 由题设得＞6，解得.所以的取值范围为（2，+∞）. ‎ ‎【2015课标Ⅱ卷】设均为正数，且，证明：‎ ‎（Ⅰ）若，则；‎ ‎（Ⅱ）是的充要条件．‎ ‎【解析】（Ⅰ）因为，，由题设，，得．因此．‎ ‎（Ⅱ）（ⅰ）若，则．即．因为，所以，由（Ⅰ）得．‎ ‎（ⅱ）若，则.‎ 即．因为，所以.‎ 于是．因此.‎ 综上，是的充要条件．‎