高三数学文科高考总复习升级增分训练概率与统计含解析 7页

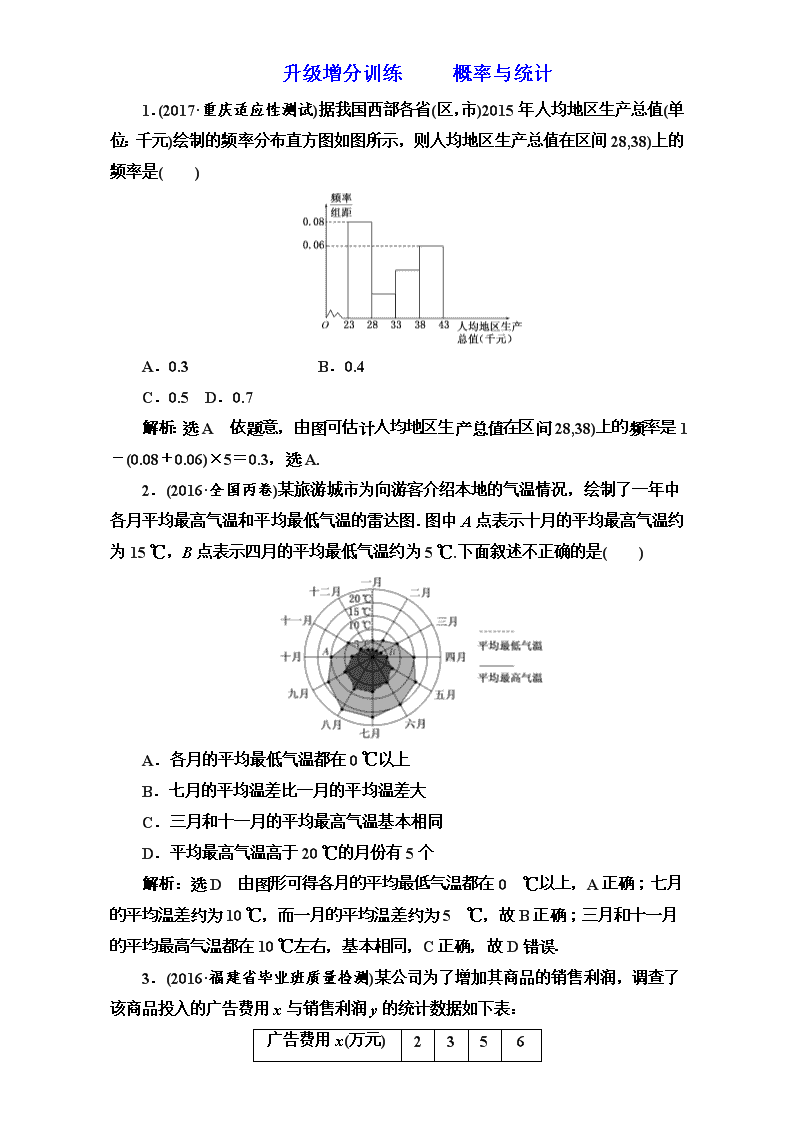
升级增分训练 概率与统计 ‎1．(2017·重庆适应性测试)据我国西部各省(区，市)2015年人均地区生产总值(单位：千元)绘制的频率分布直方图如图所示，则人均地区生产总值在区间28,38)上的频率是(　　)‎ A．0.3　　　　　　　　B．0.4‎ C．0.5 D．0.7‎ 解析：选A　依题意，由图可估计人均地区生产总值在区间28,38)上的频率是1－(0.08＋0.06)×5＝0.3，选A.‎ ‎2．(2016·全国丙卷)某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图．图中A点表示十月的平均最高气温约为‎15 ℃‎，B点表示四月的平均最低气温约为‎5 ℃‎.下面叙述不正确的是(　　)‎ A．各月的平均最低气温都在‎0 ℃‎以上 B．七月的平均温差比一月的平均温差大 C．三月和十一月的平均最高气温基本相同 D．平均最高气温高于‎20 ℃‎的月份有5个 解析：选D　由图形可得各月的平均最低气温都在‎0 ℃‎以上，A正确；七月的平均温差约为‎10 ℃‎，而一月的平均温差约为‎5 ℃‎，故B正确；三月和十一月的平均最高气温都在‎10 ℃‎左右，基本相同，C正确，故D错误．‎ ‎3．(2016·福建省毕业班质量检测)某公司为了增加其商品的销售利润，调查了该商品投入的广告费用x与销售利润y的统计数据如下表：‎ 广告费用x(万元)‎ ‎2‎ ‎3‎ ‎5‎ ‎6‎ 销售利润y(万元)‎ ‎5‎ ‎7‎ ‎9‎ ‎11‎ 由表中数据，得线性回归方程l：＝x＋，则下列结论错误的是(　　)‎ A.＞0 B.＞0‎ C．直线l过点(4,8) D．直线l过点(2,5)‎ 解析：选D　因为＝4，＝8，‎ 所以回归直线l过样本的中心点(4,8)，‎ 所以选项C正确；‎ 因为＝1.4＞0，＝－＝8－1.4×4＝2.4＞0，‎ 所以选项A、B都是正确的；‎ ＝1.4x＋2.4，因为1.4×2＋2.4＝5.2≠5，‎ 所以点(2,5)不在直线l上，所以选项D是错误的，故选D.‎ ‎4．面对竞争日益激烈的消费市场，众多商家不断扩大自己的销售市场，以降低生产成本．某白酒酿造企业市场部对该企业9月份的产品销量(单位：千箱)与单位成本(单位：元)的资料进行线性回归分析，得到结果如下：‎ ＝，＝71，＝79，iyi＝1 481.‎ 则销量每增加1千箱，单位成本约下降________元(结果保留5位有效数字)．‎ 附：回归直线的斜率和截距的最小二乘法公式分别为：‎ ＝，＝－.‎ 解析：由题意知＝≈－1.818 2，‎ ＝71－(－1.818 2)×≈77.364，‎ 所以＝－1.818 2x＋77.364，‎ 所以销量每增加1千箱，‎ 则单位成本约下降1.818 2元．‎ 答案：1.818 2‎ ‎5．从甲、乙两部门中各任选10名员工进行职业技能测试，测试成绩(单位：分)数据的茎叶图如图1所示：‎ ‎(1)分别求出甲、乙两组数据的中位数，并比较两组数据的分散程度(只需给出结论)；‎ ‎(2)甲组数据频率分布直方图如图2所示，求a，b，c的值；‎ ‎(3)从甲、乙两组数据中各任取一个，求所取两数之差的绝对值大于20的概率．‎ 解：(1)甲组数据的中位数为＝78.5，‎ 乙组数据的中位数为＝78.5.‎ 从茎叶图可以看出，甲组数据比较集中，乙组数据比较分散．‎ ‎(2)由茎叶图知，甲组中60,70)的人数为1，故c＝0.01.‎ ‎70,80)的人数为5人，故a＝0.05.‎ ‎80,90)，90,100]的人数分别为2人，‎ 故b＝0.02.‎ ‎(3)从甲、乙两组数据中各任取一个，‎ 得到的所有基本事件共有100个，其中满足“两数之差的绝对值大于‎20”‎的基本事件有16个，‎ 故所求概率P＝＝.‎ ‎6．(2017·合肥质检)某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ y ‎0.02‎ ‎0.05‎ ‎0.1‎ ‎0.15‎ ‎0.18‎ ‎(1)根据上表中的数据，用最小二乘法求出y关于x的线性回归方程；‎ ‎(2)根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过0.5%(精确到月)．‎ 附：＝，＝－.‎ 解：(1)由数据得＝(1＋2＋3＋4＋5)＝3，‎ ＝(0.02＋0.05＋0.1＋0.15＋0.18)＝0.1，‎ iyi＝0.02＋2×0.05＋3×0.1＋4×0.15＋5×0.18＝1.92.‎ ＝12＋22＋32＋42＋52＝55.‎ ‎5 ＝5×3×0.1＝1.5，‎ ‎52＝45，‎ 故＝＝0.042.‎ ＝0.1－0.042×3＝－0.026，‎ 所以线性回归方程为＝0.042x－0.026.‎ ‎(2)由上面的回归方程可知，上市时间与市场占有率正相关，‎ 即上市时间每增加1个月，市场占有率都增加0.042个百分点．‎ 由＝0.042x－0.026＞0.5，解得x≥13，‎ 故预计上市13个月时，该款旗舰机型市场占有率能超过0.5%.‎ ‎7．(2016·北京高考)某市居民用水拟实行阶梯水价，每人月用水量中不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费．从该市随机调查了10 000位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图：‎ ‎(1)如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？‎ ‎(2)假设同组中的每个数据用该组区间的右端点值代替．当w＝3时，估计该市居民该月的人均水费．‎ 解：(1)由用水量的频率分布直方图，知该市居民该月用水量在区间0.5,1]，(1,1.5]，(1.5,2]，(2,2.5]，(2.5,3]内的频率依次为0.1,0.15,0.2,0.25,0.15.‎ 所以该月用水量不超过‎3立方米的居民占85%，用水量不超过‎2立方米的居民占45%.‎ 依题意，w至少定为3.‎ ‎(2)由用水量的频率分布直方图及题意，得居民该月用水费用的数据分组与频率分布表如下：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 分组 ‎2,4]‎ ‎(4,6]‎ ‎(6,8]‎ ‎(8,10]‎ ‎(10,12]‎ ‎(12,17]‎ ‎(17,22]‎ ‎(22,27]‎ 频率 ‎0.1‎ ‎0.15‎ ‎0.2‎ ‎0.25‎ ‎0.15‎ ‎0.05‎ ‎0.05‎ ‎0.05‎ 根据题意，该市居民该月的人均水费估计为 ‎4×0.1＋6×0.15＋8×0.2＋10×0.25＋12×0.15＋17×0.05＋22×0.05＋27×0.05＝10.5(元)．‎ ‎8．(2016·云南省统测)某校高二年级共有1 600名学生，其中男生960名，女生640名．该校组织了一次满分为100分的数学学业水平模拟考试．根据研究，在正式的学业水平考试中，本次成绩在80,100]的学生可取得A等(优秀)，在60,80)的学生可取得B等(良好)，在40,60)的学生可取得C等(合格)，不到40分的学生只能取得D等(不合格)．为研究这次考试成绩优秀是否与性别有关，现按性别采用分层抽样的方法抽取100名学生，将他们的成绩按从低到高分成30,40)，40,50)，50,60)，60,70)，70,80)，80,90)，90,100]七组加以统计，绘制成如图所示的频率分布直方图．‎ ‎(1)估计该校高二年级学生在正式的数学学业水平考试中成绩不合格的人数；‎ ‎(2)请你根据已知条件将下列2×2列联表补充完整．并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”？‎ 数学成绩优秀 数学成绩不优秀 合计 男生 a＝12‎ b＝‎ 女生 c＝‎ d＝34‎ 合计 n＝100‎ 附：K2＝ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ 解：(1)设抽取的100名学生中，本次考试成绩不合格的有x人，‎ 根据题意得x＝100×1－10×(0.006＋0.012×2＋0.018＋0.024＋0.026)]＝2.‎ 据此估计该校高二年级学生在正式的数学学业水平考试中成绩不合格的人数为×1 600＝32.‎ ‎(2)根据已知条件得2×2列联表如下：‎ 数学成绩优秀 数学成绩不优秀 合计 男生 a＝12‎ b＝48‎ ‎60‎ 女生 c＝6‎ d＝34‎ ‎40‎ 合计 ‎18‎ ‎82‎ ‎100‎ ‎∵K2＝≈0.407＜2.706，‎ ‎∴没有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”．‎