高考一轮复习数学资料赢在高考 41 5页

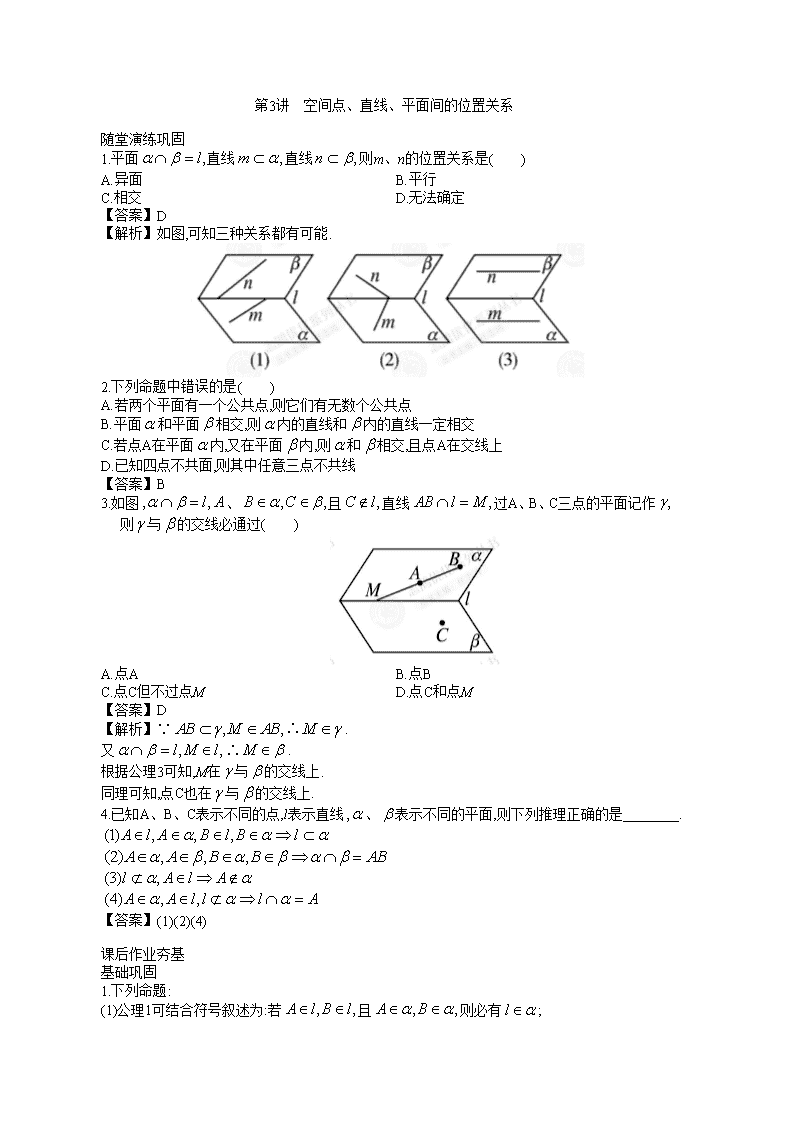
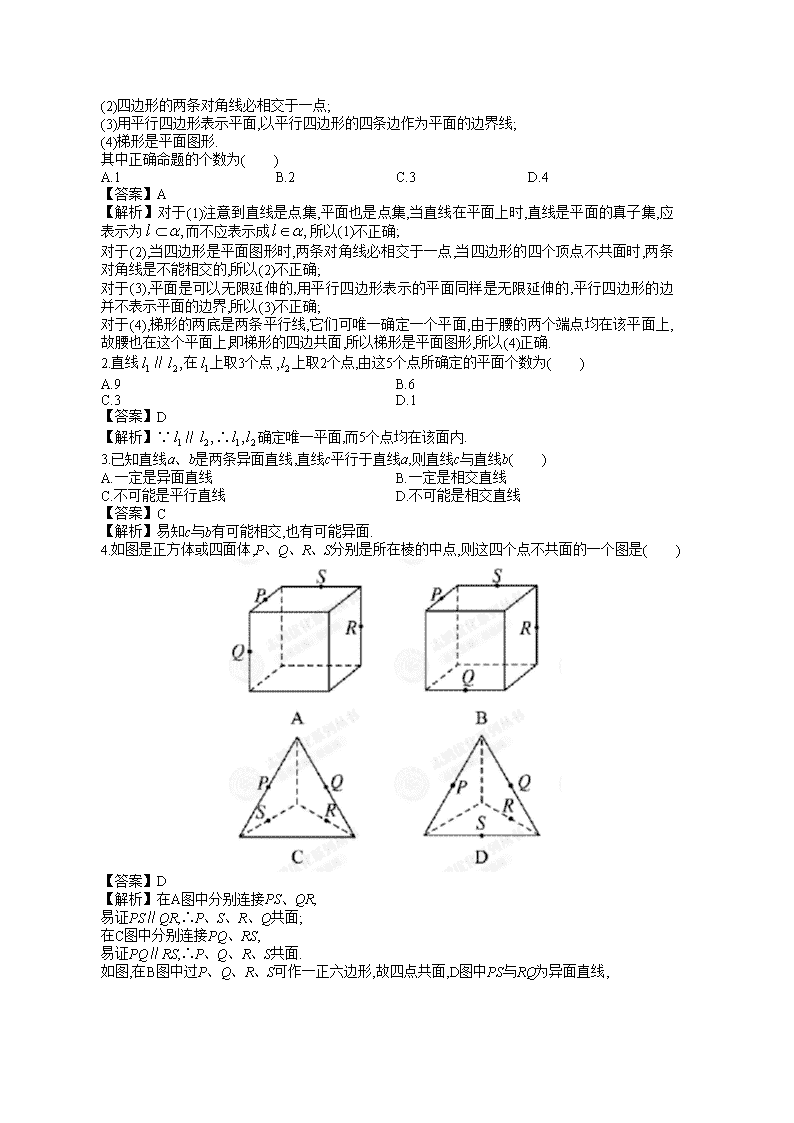
‎ 第3讲 空间点、直线、平面间的位置关系 随堂演练巩固 ‎1.平面直线直线则m、n的位置关系是( ) ‎ A.异面 B.平行 ‎ C.相交 D.无法确定 ‎ ‎【答案】D ‎ ‎【解析】如图,可知三种关系都有可能. ‎ ‎ ‎ ‎2.下列命题中错误的是( ) ‎ A.若两个平面有一个公共点,则它们有无数个公共点 ‎ B.平面和平面相交,则内的直线和内的直线一定相交 ‎ C.若点A在平面内,又在平面内,则和相交,且点A在交线上 ‎ D.已知四点不共面,则其中任意三点不共线 ‎ ‎【答案】B ‎3.如图、且直线过A、B、C三点的平面记作则与的交线必通过( ) ‎ ‎ ‎ A.点A B.点B ‎ C.点C但不过点M D.点C和点M ‎ ‎【答案】D ‎ ‎【解析】∵∴. ‎ 又∴. ‎ 根据公理3可知,M在与的交线上. ‎ 同理可知,点C也在与的交线上. ‎ ‎4.已知A、B、C表示不同的点,l表示直线、表示不同的平面,则下列推理正确的是 . ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎【答案】(1)(2)(4) ‎ 课后作业夯基 基础巩固 ‎1.下列命题: ‎ ‎(1)公理1可结合符号叙述为:若且则必有; ‎ ‎(2)四边形的两条对角线必相交于一点; ‎ ‎(3)用平行四边形表示平面,以平行四边形的四条边作为平面的边界线; ‎ ‎(4)梯形是平面图形. ‎ 其中正确命题的个数为( ) ‎ A.1 B.2 C.3 D.4 ‎ ‎【答案】A ‎ ‎【解析】对于(1)注意到直线是点集,平面也是点集,当直线在平面上时,直线是平面的真子集,应表示为而不应表示成所以(1)不正确; ‎ 对于(2),当四边形是平面图形时,两条对角线必相交于一点,当四边形的四个顶点不共面时,两条对角线是不能相交的,所以(2)不正确; ‎ 对于(3),平面是可以无限延伸的,用平行四边形表示的平面同样是无限延伸的,平行四边形的边并不表示平面的边界,所以(3)不正确; ‎ 对于(4),梯形的两底是两条平行线,它们可唯一确定一个平面,由于腰的两个端点均在该平面上,故腰也在这个平面上,即梯形的四边共面,所以梯形是平面图形,所以(4)正确. ‎ ‎2.直线∥在上取3个点上取2个点,由这5个点所确定的平面个数为( ) ‎ A.9 B.6 ‎ C.3 D.1 ‎ ‎【答案】D ‎ ‎【解析】∵∥∴确定唯一平面,而5个点均在该面内. ‎ ‎3.已知直线a、b是两条异面直线,直线c平行于直线a,则直线c与直线b( ) ‎ A.一定是异面直线 B.一定是相交直线 ‎ C.不可能是平行直线 D.不可能是相交直线 ‎ ‎【答案】C ‎ ‎【解析】易知c与b有可能相交,也有可能异面. 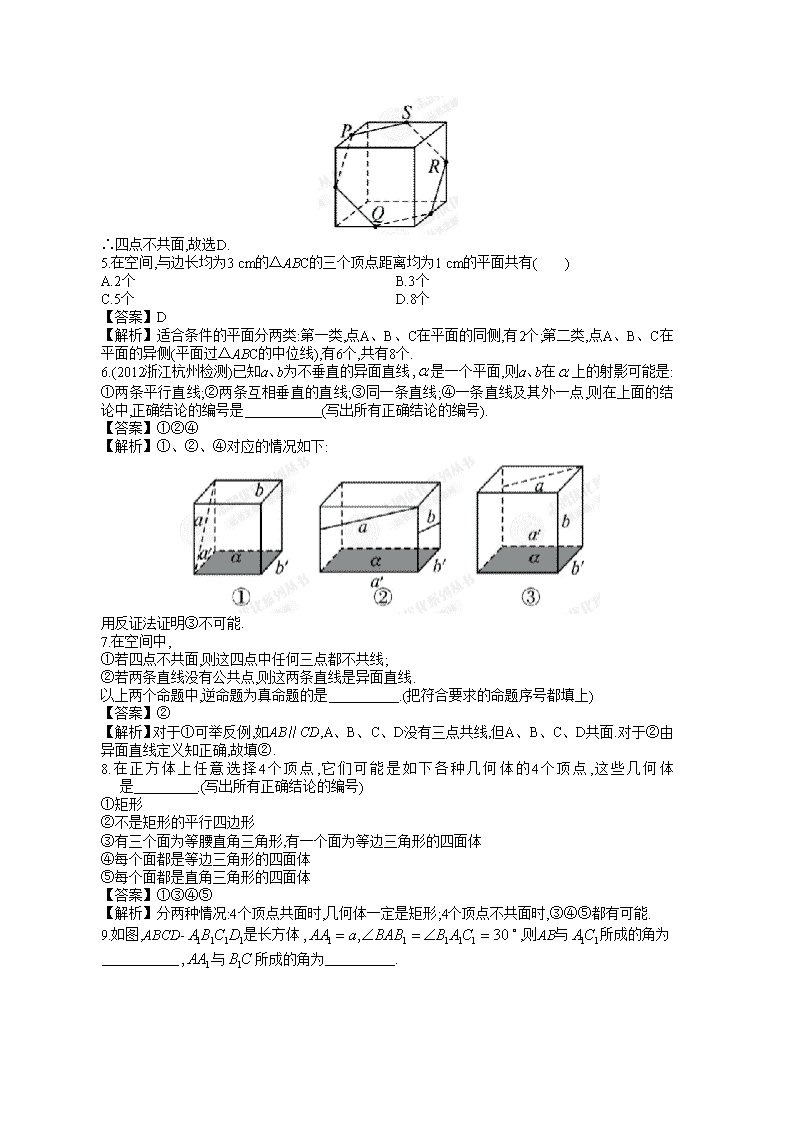‎ ‎4.如图是正方体或四面体,P、Q、R、S分别是所在棱的中点,则这四个点不共面的一个图是( ) ‎ ‎ ‎ ‎【答案】D ‎ ‎【解析】在A图中分别连接PS、QR, ‎ 易证PS∥QR,∴P、S、R、Q共面; ‎ 在C图中分别连接PQ、RS, ‎ 易证PQ∥RS,∴P、Q、R、S共面. ‎ 如图,在B图中过P、Q、R、S可作一正六边形,故四点共面,D图中PS与RQ为异面直线, ‎ ‎ ‎ ‎∴四点不共面,故选D. ‎ ‎5.在空间,与边长均为3 cm的△ABC的三个顶点距离均为1 cm的平面共有( ) ‎ A.2个 B.3个 ‎ C.5个 D.8个 ‎ ‎【答案】D ‎ ‎【解析】适合条件的平面分两类:第一类,点A、B、C在平面的同侧,有2个;第二类,点A、B、C在平面的异侧(平面过△ABC的中位线),有6个,共有8个. ‎ ‎6.(2012浙江杭州检测)已知a、b为不垂直的异面直线是一个平面,则a、b在上的射影可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点,则在上面的结论中,正确结论的编号是 (写出所有正确结论的编号). ‎ ‎【答案】①②④ ‎ ‎【解析】①、②、④对应的情况如下: ‎ ‎ ‎ 用反证法证明③不可能. ‎ ‎7.在空间中, ‎ ‎①若四点不共面,则这四点中任何三点都不共线; ‎ ‎②若两条直线没有公共点,则这两条直线是异面直线. ‎ 以上两个命题中,逆命题为真命题的是 .(把符合要求的命题序号都填上) ‎ ‎【答案】② ‎ ‎【解析】对于①可举反例,如AB∥CD,A、B、C、D没有三点共线,但A、B、C、D共面.对于②由异面直线定义知正确,故填②.‎ ‎8.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是 .(写出所有正确结论的编号) ‎ ‎①矩形 ‎ ‎②不是矩形的平行四边形 ‎ ‎③有三个面为等腰直角三角形,有一个面为等边三角形的四面体 ‎ ‎④每个面都是等边三角形的四面体 ‎ ‎⑤每个面都是直角三角形的四面体 ‎ ‎【答案】①③④⑤ ‎ ‎【解析】分两种情况:4个顶点共面时,几何体一定是矩形;4个顶点不共面时,③④⑤都有可能. ‎ ‎9.如图,ABCD-是长方体,则AB与所成的角为 ‎ 与所成的角为 . ‎ ‎ ‎ ‎【答案】30 45 ‎ ‎【解析】∵AB∥∴是AB与所成的角, ‎ ‎∴AB与所成的角为30. ‎ ‎∵∥∴是与所成的角. ‎ 由已知条件可以得出 ‎ ‎∴. ‎ ‎∴四边形是正方形.∴. ‎ ‎10.不重合的三条直线,若相交于一点,最多能确定 个平面;若相交于两点,最多能确定 个平面;若相交于三点,最多能确定 个平面. ‎ ‎【答案】3 2 1 ‎ ‎【解析】三条直线相交于一点,最多可确定3个平面,如图(1);三条直线相交于两点,最多可确定2个平面,如图(2);三条直线相交于三点,最多可确定1个平面,如图(3). ‎ ‎ ‎ ‎11.已知平面、、两两相交于直线、、且与相交于点P,求证:、、三线共点. ‎ ‎【证明】如图所示,‎ ‎ ‎ ‎∵ ‎ ‎∴且. ‎ 又∴. ‎ ‎∴.又 ‎ ‎∴.∴. ‎ ‎∵∴. ‎ ‎∴、、共点于点P. ‎ ‎12.如图,已知平面且.设梯形ABCD中,AD∥BC,且 ‎.求证:AB,CD,l共点(相交于一点). ‎ ‎ ‎ ‎【证明】∵梯形ABCD中,AD∥BC, ‎ ‎∴AB,CD是梯形ABCD的两腰. ‎ ‎∴AB,CD必定相交于一点. ‎ 设. ‎ 又∵∴且. ‎ ‎∴. ‎ 又∵∴ ‎ 即AB,CD,l共点. ‎ 拓展延伸 ‎13.有一矩形纸片ABCD,AB=5,BC=2,E、F分别是AB、CD上的点,且BE=CF=1,如图(1).现在把纸片沿EF折成图(2)形状,且. ‎ ‎ ‎ ‎(1)求BD的长; ‎ ‎(2)求证:AC,BD交于一点且被该点平分. ‎ ‎【解】(1)将平面BF折起后,补成长方体AEFD—则BD恰好是长方体的一条对角线. ‎ 因为AE、EF、EB两两垂直, ‎ ‎ ‎ 所以BD恰好是以AE、EF、EB为长、宽、高的长方体的对角线. ‎ 所以. ‎ ‎(2)证明:因为AD 所以点A、D、B、C在同一平面内,且四边形ABCD为平行四边形. ‎ 所以AC、BD交于一点且被该点平分. ‎