浙江省杭州市第二中学高三月高考模拟数学试题 15页

绝密★启用前 ‎2019 年杭州二中高考数学模拟试题 姓名： 准考证号： ‎ 本试题卷分选择题和非选择题两部分。全卷共 4 页，选择题部分 1 至 3 页；非选择题部 ‎3 至 4 页。满分 150 分。考试用时 120 分钟。‎ 考生注意：‎ ‎1．答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题 卷和答题纸规定的位置上。‎ ‎2．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答， 在本试题卷上的作答一律无效。‎ 选择题部分 (共 40 分)‎ 一、选择题：本大题共 10 小题，每小题 4 分，共 40 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。‎ ‎1.设集合 A = {1, 2, 5} ， B = {2, 4} ， C = {x Î R | -1 £ x < 5} ，则 ( A U B) I C = A.{1, 2, 4, 6} B.{x Î R | -1 £ x £ 5} C.{2} D.{1, 2, 4}‎ ‎2.双曲线的焦点坐标为 A. (-1, 0) ， (1, 0) B. (-, 0) ， ( , 0)‎ C. (0, - ) ， (0, ) D. 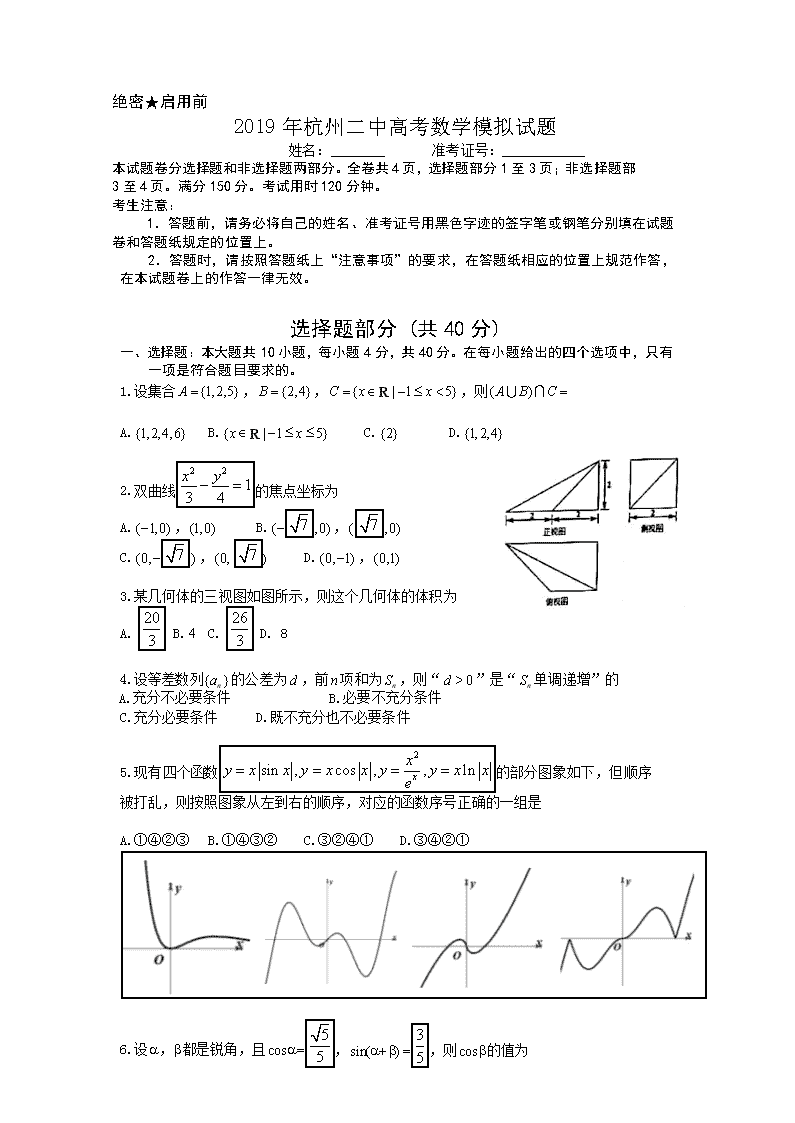(0, -1) ， (0,1)‎ ‎3.某几何体的三视图如图所示，则这个几何体的体积为 A. B. 4 C. D. 8‎ ‎4.设等差数列{an } 的公差为 d ，前 n 项和为 Sn ，则“ d > 0 ”是“ Sn 单调递增”的 A.充分不必要条件 B.必要不充分条件 ‎ C.充分必要条件 D.既不充分也不必要条件 ‎5.现有四个函数的部分图象如下，但顺序 被打乱，则按照图象从左到右的顺序，对应的函数序号正确的一组是 A.①④②③ B.①④③② C.③②④① D.③④②①‎ ‎6.设a ， b 都是锐角，且 cosa =， sin(a+ b) =，则 cos b的值为 ‎7.已知函数，若实数 m Î (0,1) ，则函数 g (x) = f (x) - m 的零点个数为 A. 0 B.1 C. 2 D. 3‎ ‎8.已知甲盒中有 2 个红球，1 个蓝球，乙盒中有1 个红球， 2 个蓝球，从甲乙两个盒中各取1‎ 球放入原来为空的丙盒中.现从甲、乙、丙三个盒子中分别取1 个球，记红球的个数为 xi (i = 1, 2, 3) ，则 A. E (x1 ) > E (x3) > E (x2 ) ， D(x1) = D(x2 ) > D(x3)‎ B. E (x1 ) < E (x3)< E (x2 ) ，D(x1) = D(x2 ) > D(x3)‎ C. E (x1 ) > E (x3) > E (x2 ) ，D(x1) = D(x2 ) < D(x3)‎ D. E (x1 ) < E (x3)< E (x2 ) ，D(x1) = D(x2 ) < D(x3)‎ ‎9.设 ， 为单位向量，向量 满足| 2 + |=| × | ，则 | - | 的最大值为 A. 2 B.1 C. D. ‎ ‎10. 如图，三棱锥 P - ABC 中， PA ^ 平面 ABC ， ÐBAC = ， Q 为 PA 中点，下列说法中 ‎（1） ÐPBA + ÐPCA + ÐBPC = p ；‎ ‎（2）记二面角 P - BC - A ， Q - BC - A 的平面角分别为q1 ，q2 ，q1 > 2q2 ；‎ ‎（3）记 △ABC ，△QBC ，△PBC 的面积分别为 S0 ， S1 ， S2 ，‎ ‎（4） cos ÐPBC < cos ÐPBQ ×cos ÐQBC ，‎ 正确说法的个数为 A. 0 B.1 ‎ C. 2 D. 3‎ 非选择题部分（共 110 分）‎ 二、填空题：本大题共 7 小题，多空题每题 6 分，单空题每题 4 分，共 36 分。‎ ‎11. 欧拉公式 eix = cos x + i sin x （ i 为虚数单位）是有瑞士著名数学家欧拉发现的，它将 函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里非常 重要，被誉为“数学中的天桥”.根据欧拉公式可知，对表示的复数 ，则| z | 等 于 ；等于 .‎ ‎12. 的展开式共有11 项，则 n 的值为 ，其中常数项为 .‎ ‎13. 设 x ， y 满足约束条件，则 z = - x + y 的最小值是 ，最大值是 .‎ ‎14. 在 △ABC 中，sin( A + ) = ，0 < A < ，AC = 5 ，AB = 3 ，则 sin A 的值为 ，‎ BC 的长为 .‎ ‎15. 10 次投篮中，投中 5 次，其中恰有一个 2 连中和一个 3 连中的情形有 种（用数 字作答）. ‎ ‎16. 存在第一象限的点 M (x0, y0 )在椭圆 (a > b > 0) 上，使得过点 M 且与椭圆在此 点的切线垂直的直线经过点 ( , 0) （ c 为椭圆半焦距），则椭圆离心率的取 值范围是 .‎ ‎17. 函数 f ( x) = x3 - | ax 2 - b | -1 在 (0, 2) 上有 2 个零点，则的范围是 .‎ 三、解答题：本大题有 5 小题，共 74 分。解答应写出文字说明、证明过程或演算步骤。‎ ‎18. (本题满分 14 分)设函数 f ( x) = 3sin(w x +),w> 0, 且以为最小正周期.‎ ‎（Ｉ）求 f ( x) 的解析式；‎ ‎（Ⅱ）求 f ( x) 的对称轴方程及单调递区间.‎ ‎19. (本题满分 15 分)如图,矩形 ADFE 和梯形 ABCD 所在平面互相垂直, AB / /CD ,‎ ÐABC = ÐADB = 90° , CD = 1, BC = 2.‎ ‎（Ｉ）求证: BE //平面 DCF ；‎ ‎（Ⅱ）当 AE 的长为何值时，直线 AD 与平面 BCE 所成角的大小为 45° ?‎ ‎20. (本题满分 15 分)已知数列{an }为等比数列,数列{bn }满足 bn = log2 an ,且 a4 = b5 = 1.设 Sn为数列{bn }的前 n 项和.‎ ‎（Ｉ）求数列{an }、{bn }的通项公式及 Sn ；‎ ‎（Ⅱ）若数列{cn }满足,求{c } 的前 n 项和 T .‎ ‎21. (本题满分 15 分)如图,过抛物线 C : y2 = 2 px ( p > 0) 的焦点 F 的直线与抛物线 C 交 于 A、B 两点,过 AB 中点 M 且与 AB 垂直的直线与 x 轴交于点 N .‎ ‎（Ｉ）求的值；‎ ‎（Ⅱ）若 p = 2,求的取值范围.‎ ‎22.（本小题满分 15 分）已知 f (x) = ‎（Ｉ）求函数 y = f ( x) 有三个零点，求实数 a 的取值范围；‎ ‎（Ⅱ）若 a =2，设，其中 b £ 2, c > 0, f (x) = g (x) 的两根为 x1 , x2 ( x1 < x2)‎ 求证： x2 f ( x1 ) < x1 f ( x2 ) < 0 .‎