全国高考文科数学试题及答案重庆卷二次校对 9页

‎2012年普通高等学校招生全国统一考试（重庆卷）‎ 数学（文）试题 一、 选择题：本大题共10小题，每小题5分，共50分 ，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎（1）命题“若p则q”的逆命题是 ‎ A． 若q则p B． 若﹃p则﹃q ‎ C． 若﹃q则﹃p D． 若p则﹃q ‎（2）不等式的解集为 ‎ A．（1，+∞） B．（- ∞,-2）‎ ‎ C．（-2,1） D．（- ∞,-2）∪（1，+∞）‎ ‎（3）设A，B为直线y=x与圆x2+y2=1的两个交点，则|AB|=‎ ‎ A．1 B． C． D．2‎ ‎（4）（1-3x）5的展开式中x3的系数为 ‎ A．-270 B．‎-90 ‎C．90 D．270‎ ‎（5）-‎ ‎ A．- B- C． D． ‎ ‎（6）设x∈R,向量a=（x,1）,b=（1，-2），且a⊥b,则|a+b|=‎ ‎ A． B． C． D．10‎ ‎（7）已知a=，b=，c=log32，则a，b，c的大小关系是 ‎ （A）a=b＜c （B）a=b＞c ‎ （C）a＜b＜c （D）a＞b＞c ‎（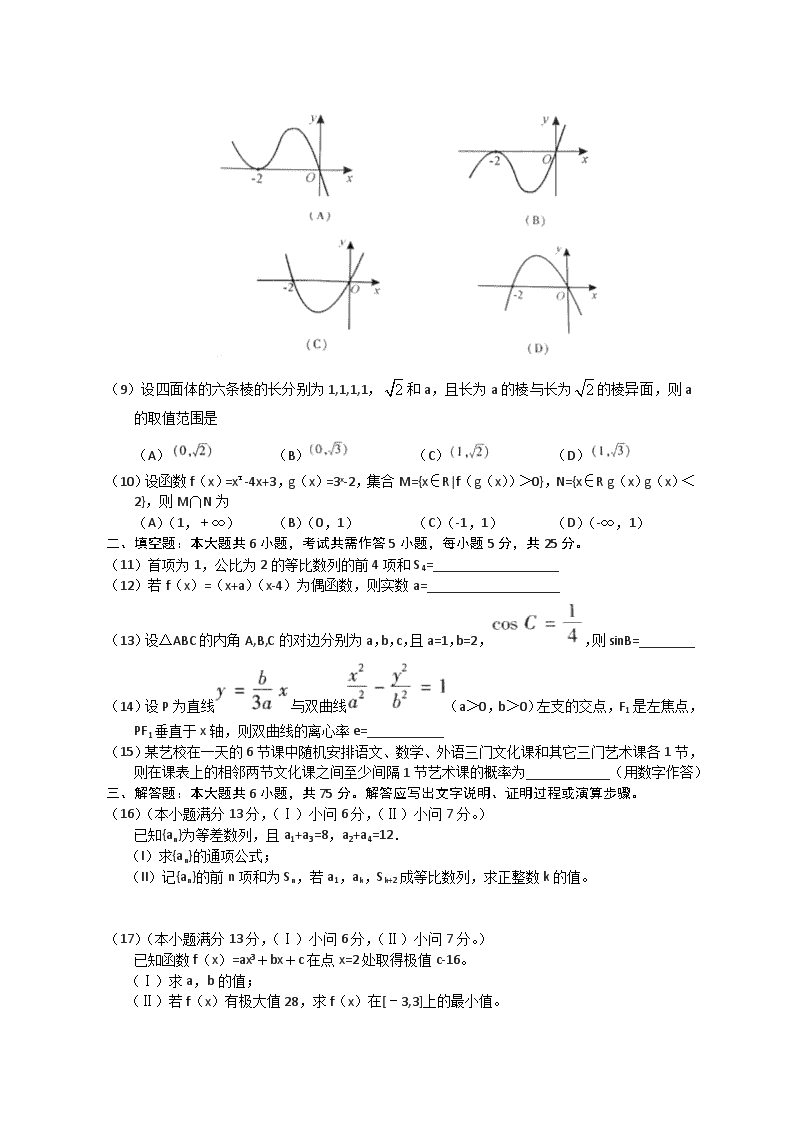8）设函数f（x）在R上可导，其导函数为f′（x），且函数f（x）在x=-2处取得极小值，则函数y=xf′（x）的图像可能是 ‎（9）设四面体的六条棱的长分别为1,1,1,1，和a，且长为a的棱与长为的棱异面，则a的取值范围是 ‎ （A） （B） （C） （D） ‎ ‎（10）设函数f（x）=x²-4x+3，g（x）=3x-2，集合M={x∈R|f（g（x））＞0}，N={x∈R g（x）g（x）＜2}，则M∩N为 ‎ （A）（1，﹢∞） （B）（0，1） （C）（-1，1） （D）（-∞，1）‎ 二、填空题：本大题共6小题，考试共需作答5小题，每小题5分，共25分。‎ ‎（11）首项为1，公比为2的等比数列的前4项和S4=__________________‎ ‎（12）若f（x）=（x+a）（x-4）为偶函数，则实数a=___________________‎ ‎（13）设△ABC的内角A,B,C的对边分别为a，b，c，且a=1，b=2，，则sinB=________‎ ‎（14）设P为直线与双曲线（a＞0，b＞0）左支的交点，F1是左焦点，PF1垂直于x轴，则双曲线的离心率e=___________‎ ‎（15）某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其它三门艺术课各1节，则在课表上的相邻两节文化课之间至少间隔1节艺术课的概率为____________（用数字作答）‎ 三、解答题：本大题共6小题，共75分。解答应写出文字说明、证明过程或演算步骤。‎ ‎（16）（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分。）‎ ‎ 已知{an}为等差数列，且a1+a3=8，a2+a4=12．‎ ‎ （I）求{an}的通项公式；‎ ‎ （II）记{an}的前n项和为Sn，若a1，ak，Sk+2成等比数列，求正整数k的值。‎ ‎（17）（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分。）‎ 已知函数f（x）=ax3＋bx＋c在点x=2处取得极值c-16。‎ ‎（Ⅰ）求a，b的值；‎ ‎（Ⅱ）若f（x）有极大值28，求f（x）在[﹣3,3]上的最小值。‎ ‎（18）（本小题满分13分，（Ⅰ）小问7分，（Ⅱ）小问6分。）‎ 甲、乙两人轮流投篮，每人每次投一球。约定甲先投且先投中者获胜，一直到有人获胜或每人都已投球三次时投篮结束。设甲每次投篮投中的概率为，乙每次投篮投中的概率为，且各次投篮互不影响。‎ ‎（Ⅰ）求乙获胜的概率；‎ ‎（Ⅱ）求投篮结束时乙只投了2个球的概率。‎ ‎（19）（本小题满分12分，（Ⅰ）小问5分，（Ⅱ）小问7分。）‎ 设函数f（x）=Asin（）（其中A＞0，＞0，-π＜≤π）在x=处取得最大值2，其图像与x轴的相邻两个交点的距离为。‎ ‎（Ⅰ）求f（x）的解析式；‎ ‎（Ⅱ）求函数g（x）=的值域。‎ ‎20．（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分）‎ 如图（20），在直三棱柱ABC-A1B‎1C1中，AB=4，AC=BC=3，D为AB的中点。‎ ‎（Ⅰ）求异面直线CC1和AB的距离；‎ ‎（Ⅱ）若AB1⊥A‎1C，求二面角A1—CD—B1的平面角的余弦值。‎ ‎21．（本小题满分12分，（Ⅰ）小问5分，（Ⅱ）小问7分）‎ 如题（21）图，设椭圆的中心为原点O，长轴在x轴上，上顶点为A，左、右焦点分别为F1，F2，线段OF1，OF2的中点分别为B1，B2，且△AB1B2是面积为4的直角三角形。‎ ‎（Ⅰ）求该椭圆的离心率和标准方程；‎ ‎（Ⅱ）过B1作直线交椭圆于P，Q两点，使PB2⊥QB2，求△PB2Q的面积。‎ 参考答案 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎（1）A ‎（2）【答案】：C ‎【解析】：‎ ‎【考点定位】本题考查解分式不等式时，利用等价变形转化为整式不等式解．‎ ‎（3）【答案】：D ‎【解析】：直线过圆的圆心 则2‎ ‎【考点定位】本题考查圆的性质，属于基础题．‎ ‎（4）A ‎（5）【答案】：C ‎【解析】：‎ ‎【考点定位】本题考查三角恒等变化，其关键是利用 ‎（6）【答案】：‎ ‎（7）【答案】：‎ ‎【解析】：，‎ ‎，则 ‎【考点定位】本题考查对数函数运算．‎ ‎（8）【答案】：C ‎【解析】：由函数在处取得极小值可知，，则；，则时，时 ‎【考点定位】本题考查函数的图象，函数单调性与导数的关系，属于基础题．‎ ‎（9）【答案】：A ‎ ‎【解析】：，，，‎ ‎【考点定位】本题考查棱锥的结构特征，考查空间想象能力，极限思想的应用，是中档题．．‎ ‎（10）【答案】：D ‎【解析】：由得则或即或 所以或；由得即所以故 二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。‎ ‎（11）【答案】：15‎ ‎【解析】：‎ ‎【考点定位】本题考查等比数列的前n项和公式 ‎（12）4‎ ‎（13）【答案】：‎ ‎（14）‎ ‎（15）【答案】：‎ 三、解答题：本大题共6小题，共75分。解答应写出文字说明、证明过程或演算步骤。‎ ‎16．【答案】：（Ⅰ）（Ⅱ）‎ ‎【解析】：：（Ⅰ）设数列 的公差为d,由题意知 解得 所以 ‎（Ⅱ）由（Ⅰ）可得 因 成等比数列，所以 从而 ，即 ‎ 解得 或（舍去），因此 。‎ ‎17．【答案】：（Ⅰ）（Ⅱ）‎ ‎【解析】：：（Ⅰ）因 故 由于 在点 处取得极值 故有即 ，化简得解得 ‎（Ⅱ）由（Ⅰ）知 ，‎ 令 ，得当时，故在上为增函数；‎ 当 时， 故在 上为减函数 当 时 ，故在 上为增函数。‎ 由此可知 在 处取得极大值， 在 处取得极小值由题设条件知 得此时，因此 上的最小值为 ‎【考点定位】本题主要考查函数的导数与极值，最值之间的关系，属于导数的应用．（1）先对函数进行求导，根据=0，，求出a，b的值．（1）根据函数=x3-3ax2+2bx在x=1处有极小值-1先求出函数中的参数a，b的值，再令导数等于0，求出极值点，判断极值点左右两侧导数的正负，当左正右负时有极大值，当左负右正时有极小值．再代入原函数求出极大值和极小值．（2）列表比较函数的极值与端点函数值的大小，端点函数值与极大值中最大的为函数的最大值，端点函数值与极小值中最小的为函数的最小值．‎ ‎18．【答案】：（Ⅰ）（Ⅱ）‎ 独立事件同时发生的概率计算公式知 ‎19．‎ ‎【答案】：（Ⅰ）（Ⅱ）‎ 因，且 ‎ 故 的值域为 ‎（20）【答案】：（Ⅰ）（Ⅱ）‎ ‎【解析】：（Ⅰ）如答（20）图1，因AC=BC， D为AB的中点，故CD AB。又直三棱柱中， 面 ，故 ，所以异面直线 和AB的距离为 ‎（Ⅱ）：由故 面 ，从而 ，故 为所求的二面角的平面角。‎ 因是在面上的射影，又已知 由三垂线定理的逆定理得从而，都与互余，因此，所以≌，因此得 从而 所以在中，由余弦定理得 ‎（21）【答案】：（Ⅰ）+=1（Ⅱ）‎ ‎， ‎ ‎（*）‎ 设 则 是上面方程的两根，因此 ‎ 又，所以 由 ，知 ，即 ，解得 当 时，方程（*）化为：‎ 故 ，‎ 的面积 当 时，同理可得（或由对称性可得） 的面积 综上所述， 的面积为 。‎