上海市闵行区高考数学一模试卷理科解析版 22页

‎2016上海市闵行区高考数学一模试卷（理科）‎ ‎　‎ 一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸上相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．‎ ‎1．若复数z满足（i为虚数单位），则|z|　　　　　　．‎ ‎2．若全集U=R，函数的值域为集合A，则∁UA=　　　　　　．‎ ‎3．方程4x﹣2x﹣6=0的解为　　　　　　．‎ ‎4．函数的最小正周期t=　　　　　　．‎ ‎5．不等式＞|x|的解集为　　　　　　．‎ ‎6．已知圆锥的底面半径为3，体积是12π，则圆锥侧面积等于　　　　　　．‎ ‎7．已知△ABC中，，，其中是基本单位向量，则△ABC的面积为　　　　　　．‎ ‎8．在2017年的上海高考改革方案中，要求每位考生必须在物理、化学、生物、政治、历史、地理6门学科中选择3门学科参加等级考试．小明同学决定在生物、政治、历史三门中至多选择一门，那么小明同学的选科方案有　　　　　　种．‎ ‎9．若Sn是等差数列{an}的前n项和，且，则=　　　　　　．‎ ‎10．若函数f（x）=2|x﹣a|（a∈R）满足f（1+x）=f（1﹣x），且f（x）在[m，+∞）上单调递增，则实数m的最小值等于　　　　　　．‎ ‎11．若点P、Q均在椭圆（a＞1）上运动，F1、F2是椭圆Γ的左、右焦点，则的最大值为　　　　　　．‎ ‎12．已知函数，若实数a、b、c互不相等，且满足f（a）=f（b）=f（c），则a+b+c的取值范围是　　　　　　．‎ ‎13．我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数x的不足近似值和过剩近似值分别为和（a，b，c，d∈N*），则是x的更为精确的不足近似值或过剩近似值．我们知道π=3.14159…，若令，则第一次用“调日法”后得是π的更为精确的过剩近似值，即，若每次都取最简分数，那么第四次用“调日法”后可得π的近似分数为　　　　　　．‎ ‎14．已知数列{an}的前n项和为Sn，对任意n∈N*，且（an+1﹣p）（an﹣p）＜0恒成立，则实数p的取值范围是　　　　　　．‎ ‎　‎ 二、选择题（本大题满分20分）本大题共有4题，每题只有一个正确答案.考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．‎ ‎15．若a，b∈R，且ab＞0，则“a=b”是“等号成立”的（　　）‎ A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既非充分又非必要条件 ‎16．设f（x）=2+5x+10x2+10x3+5x4+x5，则其反函数的解析式为（　　）‎ A． B． C． D．‎ ‎17．△ABC的内角A，B，C的对边分别为a，b，c，满足，则角A的范围是（　　）‎ A． B． C． D．‎ ‎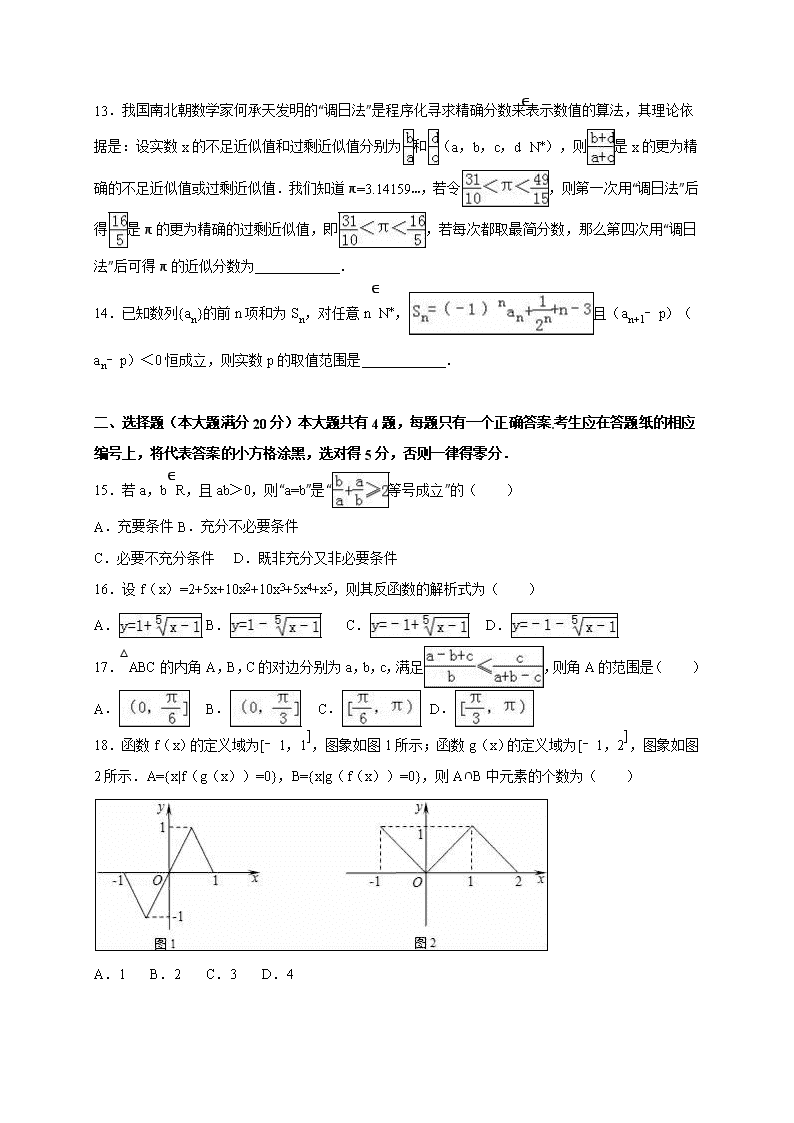18．函数f（x）的定义域为[﹣1，1]，图象如图1所示；函数g（x）的定义域为[﹣1，2]，图象如图2所示．A={x|f（g（x））=0}，B={x|g（f（x））=0}，则A∩B中元素的个数为（　　）‎ A．1 B．2 C．3 D．4‎ ‎　‎ 三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．‎ ‎19．如图，三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AA1=AB=2，BC=1，，D为棱AA1中点，证明异面直线B1C1与CD所成角为，并求三棱柱ABC﹣A1B1C1的体积．‎ ‎20．如图，点A、B分别是角α、β的终边与单位圆的交点，．‎ ‎（1）若，，求sin2β的值；‎ ‎（2）证明：cos（α﹣β）=cosαcosβ+sinαsinβ．‎ ‎21．某沿海城市的海边有两条相互垂直的直线型公路l1、l2，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个公共点P（即直线与曲线相切），如图所示．若曲线段MPN是函数图象的一段，点M到l1、l2的距离分别为8千米和1千米，点N到l2的距离为10千米，以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy，设点P的横坐标为p．‎ ‎（1）求曲线段MPN的函数关系式，并指出其定义域；‎ ‎（2）若某人从点O沿公路至点P观景，要使得沿折线OAP比沿折线OBP的路程更近，求p的取值范围．‎ ‎22．已知椭圆Γ的中心在坐标原点，且经过点，它的一个焦点与抛物线 E：y2=4x的焦点重合．‎ ‎（1）求椭圆Γ的方程；‎ ‎（2）斜率为k的直线l过点F（1，0），且与抛物线 E交于A、B两点，设点P（﹣1，k），△PAB的面积为，求k的值；‎ ‎（3）若直线l过点M（0，m）（m≠0），且与椭圆Γ交于C、D两点，点C关于y轴的对称点为Q，直线QD的纵截距为n，证明：mn为定值．‎ ‎23．已知数列{an}的各项均为整数，其前n项和为Sn．规定：若数列{an}满足前r项依次成公差为1的等差数列，从第r﹣1项起往后依次成公比为2的等比数列，则称数列{an}为“r关联数列”．‎ ‎（1）若数列{an}为“6关联数列”，求数列{an}的通项公式；‎ ‎（2）在（1）的条件下，求出Sn，并证明：对任意n∈N*，anSn≥a6S6；‎ ‎（3）已知数列{an}为“r关联数列”，且a1=﹣10，是否存在正整数k，m（m＞k），使得a1+a2+…+ak﹣1+ak=a1+a2+…+am﹣1+am？若存在，求出所有的k，m值；若不存在，请说明理由．‎ ‎　‎ ‎2016上海市闵行区高考数学一模试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸上相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．‎ ‎1．若复数z满足（i为虚数单位），则|z|　2　．‎ ‎【考点】复数求模．‎ ‎【专题】转化思想；综合法；数系的扩充和复数．‎ ‎【分析】根据复数的四则运算先化简复数，然后计算复数的长度即可 ‎【解答】解：∵，‎ ‎∴﹣z=i+1，‎ ‎∴z=﹣1﹣i，‎ ‎∴|z|==2，‎ 故答案为：2．‎ ‎【点评】本题主要考查复数的计算，要求熟练掌握复数的四则运算以及复数长度的计算公式，比较基础．‎ ‎　‎ ‎2．若全集U=R，函数的值域为集合A，则∁UA=　（﹣∞，0）　．‎ ‎【考点】补集及其运算．‎ ‎【专题】计算题．‎ ‎【分析】求出函数的值域确定出A，根据全集U=R，找出A的补集即可．‎ ‎【解答】解：函数y=x≥0，得到A=[0，+∞），‎ ‎∵全集U=R，‎ ‎∴∁UA=（﹣∞，0）．‎ 故答案为：（﹣∞，0）‎ ‎【点评】此题考查了补集及其运算，熟练掌握补集的定义是解本题的关键．‎ ‎　‎ ‎3．方程4x﹣2x﹣6=0的解为　log23　．‎ ‎【考点】指数式与对数式的互化；二次函数的性质．‎ ‎【专题】计算题．‎ ‎【分析】由4x﹣2x﹣6=0，得（2x）2﹣2x﹣6=0，由此能求出方程4x﹣2x﹣6=0的解．‎ ‎【解答】解：由4x﹣2x﹣6=0，得 ‎（2x）2﹣2x﹣6=0，‎ 解得2x=3，或2x=﹣2（舍去），‎ ‎∴x=log23．‎ 故答案为：log23．‎ ‎【点评】本题考查指数方程的解法，解题时要认真审题，注意指数式和对数式的互化．‎ ‎　‎ ‎4．函数的最小正周期t=　π　．‎ ‎【考点】二阶行列式的定义；三角函数中的恒等变换应用；三角函数的周期性及其求法．‎ ‎【专题】计算题；转化思想；综合法；三角函数的求值；矩阵和变换．‎ ‎【分析】利用二阶行列式展开式法则和余弦函数二倍角公式求解．‎ ‎【解答】解：函数 ‎=cos（π﹣x）cosx﹣sin（π+x）sinx ‎=﹣cos2x+sin2x ‎=﹣cos2x，‎ ‎∴函数的最小正周期t==π．‎ 故答案为：π．‎ ‎【点评】本题考查三角函数的最小正周期的求法，是基础题，解题时要认真审题，注意二阶行列式展开法则的合理运用．‎ ‎　‎ ‎5．不等式＞|x|的解集为　（0，2）　．‎ ‎【考点】其他不等式的解法．‎ ‎【专题】不等式的解法及应用．‎ ‎【分析】不等式即＞0，显然x＜0时不成立．当x＞0时，根据＜0，求得不等式的解集．‎ ‎【解答】解：当x＜0时，＞﹣x，即＞0，显然x＜0时不成立．‎ 当x＞0时，＜0，解得0＜x＜2，所以不等式的解集为（0，2），‎ 故答案为：（0，2）．‎ ‎【点评】本题主要考查分式不等式的解法，体现了转化以及分类讨论的数学思想，属于中档题．‎ ‎　‎ ‎6．已知圆锥的底面半径为3，体积是12π，则圆锥侧面积等于　15π　．‎ ‎【考点】棱柱、棱锥、棱台的侧面积和表面积；旋转体（圆柱、圆锥、圆台）．‎ ‎【专题】空间位置关系与距离．‎ ‎【分析】根据圆锥的体积计算出圆锥的高，以及圆锥的母线，进而求出圆锥的侧面积．‎ ‎【解答】解：设圆锥的高为h，底面半径为r，‎ ‎∵圆锥的底面半径为3，体积是12π，‎ ‎∴，‎ 即h=4，‎ ‎∴圆锥的母线长l=，‎ ‎∴圆锥的侧面积S=πrl=3×5π=15π，‎ 故答案为：15π．‎ ‎【点评】本题主要考查圆锥的体积和侧面积的计算，要求熟练掌握圆锥的体积和侧面积公式．‎ ‎　‎ ‎7．已知△ABC中，，，其中是基本单位向量，则△ABC的面积为　　．‎ ‎【考点】三角形的面积公式．‎ ‎【专题】转化思想；综合法；解三角形．‎ ‎【分析】根据平面向量的数量积以及坐标运算，求出向量的模长，判断三角形是直角三角形，求出面积即可．‎ ‎【解答】解：根据题意，得： =（4，3），=（﹣3，4），‎ ‎∴=﹣=（﹣7，1），‎ ‎∴2=42+32=25， 2=（﹣3）2+42=25， 2=（﹣7）2+12=50；‎ ‎∴||2=||2+||2，‎ ‎△ABC是直角三角形，它的面积为S=×5×5=．‎ 故答案为：．‎ ‎【点评】本题考查了平面向量的应用问题，解题时应根据平面向量的数量积以及坐标运算，进行解答，是基础题．‎ ‎　‎ ‎8．在2017年的上海高考改革方案中，要求每位考生必须在物理、化学、生物、政治、历史、地理6门学科中选择3门学科参加等级考试．小明同学决定在生物、政治、历史三门中至多选择一门，那么小明同学的选科方案有　10　种．‎ ‎【考点】排列、组合的实际应用．‎ ‎【专题】计算题；方程思想；综合法；排列组合．‎ ‎【分析】分类讨论：选择两门理科学科，一门文科学科；选择三门理科学科，即可得出结论．‎ ‎【解答】解：选择两门理科学科，一门文科学科，有C32C31=9种；选择三门理科学科，有1种，‎ 故共有10种．‎ 故答案为：10．‎ ‎【点评】本题考查计数原理的应用，考查学生的计算能力，比较基础．‎ ‎　‎ ‎9．若Sn是等差数列{an}的前n项和，且，则=　5　．‎ ‎【考点】数列的极限．‎ ‎【专题】方程思想；分析法；等差数列与等比数列．‎ ‎【分析】设等差数列{an}的公差为d，运用等差数列的求和公式，计算可得d=10，再由=0，计算即可得到所求值．‎ ‎【解答】解：设等差数列{an}的公差为d，‎ 即有Sn=na1+n（n﹣1）d，‎ 即=a1+d（n﹣1），‎ 由，可得 a1+d=a1+d+10，‎ 解得d=10，‎ 则==5+，‎ 即有=（5+）=5+‎ ‎=5+0=5．‎ 故答案为：5．‎ ‎【点评】本题考查等差数列的求和公式的运用，考查数列极限的求法，注意运用数列极限公式，属于中档题．‎ ‎　‎ ‎10．若函数f（x）=2|x﹣a|（a∈R）满足f（1+x）=f（1﹣x），且f（x）在[m，+∞）上单调递增，则实数m的最小值等于　1　．‎ ‎【考点】抽象函数及其应用．‎ ‎【专题】转化思想；数形结合法；函数的性质及应用．‎ ‎【分析】先由f（1+x）=f（1﹣x）得到f（x）的图象关于直线x=1轴对称，进而求得a=1，再根据题中所给单调区间，求出m≥1．‎ ‎【解答】解：因为f（1+x）=f（1﹣x），‎ 所以，f（x）的图象关于直线x=1轴对称，‎ 而f（x）=2|x﹣a|，所以f（x）的图象关于直线x=a轴对称，‎ 因此，a=1，f（x）=2|x﹣1|，‎ 且该函数在（﹣∞，1]上单调递减，在[1，+∞）上单调递增，‎ 又因为函数f（x）在[m，+∞）上单调递增，‎ 所以，m≥1，即实数m的最小值为1．‎ 故答案为：1．‎ ‎【点评】本题主要考查了指数型复合函数的图象与性质，涉及该函数图象的对称性和单调区间，体现了数形结合的解题思想，属于中档题．‎ ‎　‎ ‎11．若点P、Q均在椭圆（a＞1）上运动，F1、F2是椭圆Γ的左、右焦点，则的最大值为　2a　．‎ ‎【考点】椭圆的简单性质．‎ ‎【专题】数形结合；转化思想；圆锥曲线的定义、性质与方程．‎ ‎【分析】利用向量的平行四边形法则可得： =2，代入再利用向量的三角形法则、椭圆的性质即可得出．‎ ‎【解答】解：∵ =2，‎ ‎∴==2≤2a，‎ ‎∴的最大值为2a，‎ 故答案为：2a．‎ ‎【点评】本题考查了椭圆的定义及其标准方程、向量的平行四边形法则与三角形法则，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎12．已知函数，若实数a、b、c互不相等，且满足f（a）=f（b）=f（c），则a+b+c的取值范围是　（8，23）　．‎ ‎【考点】余弦函数的对称性；分段函数的应用．‎ ‎【专题】综合题；数形结合；数形结合法；函数的性质及应用；三角函数的图像与性质．‎ ‎【分析】作出函数f（x）的图象，根据f（a）=f（b）=f（c），确定a，b，c的范围，即可得出a+b+c的取值范围．‎ ‎【解答】解：作出f（x）的函数图象，如图：‎ 令log（x﹣3）+1=1，解得x=4．‎ 令log（x﹣3）+1=﹣1，解得x=19．‎ 设a＜b＜c，则a+b=4，4＜c＜19．‎ ‎∴8＜a+b+c＜23．‎ 故答案为（8，23）．‎ ‎【点评】本题以三角函数和对数函数为例，考查了函数的零点与方程根个数讨论等知识点，利用数形结合，观察图象的变化，从而得出变量的取值范围是解决本题的关键．‎ ‎　‎ ‎13．我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数x的不足近似值和过剩近似值分别为和（a，b，c，d∈N*），则是x的更为精确的不足近似值或过剩近似值．我们知道π=3.14159…，若令，则第一次用“调日法”后得是π的更为精确的过剩近似值，即，若每次都取最简分数，那么第四次用“调日法”后可得π的近似分数为　　．‎ ‎【考点】归纳推理．‎ ‎【专题】计算题；方程思想；综合法；推理和证明．‎ ‎【分析】利用“调日法”进行计算，即可得出结论．‎ ‎【解答】解：第二次用“调日法”后得是π的更为精确的过剩近似值，即＜π＜；‎ 第三次用“调日法”后得是π的更为精确的过剩近似值，即＜π＜，‎ 第四次用“调日法”后得是π的更为精确的过剩近似值，即＜π＜，‎ 故答案为：‎ ‎【点评】本题考查“调日法”，考查学生的计算能力，比较基础．‎ ‎　‎ ‎14．已知数列{an}的前n项和为Sn，对任意n∈N*，且（an+1﹣p）（an﹣p）＜0恒成立，则实数p的取值范围是　　．‎ ‎【考点】数列递推式．‎ ‎【专题】综合题；函数思想；转化思想；综合法；等差数列与等比数列．‎ ‎【分析】由数列递推式求出首项，写出n≥2时的递推式，作差后对n分偶数和奇数讨论，求出数列通项公式，可得函数（n为正奇数）为减函数，最大值为，函数（n为正偶数）为增函数，最小值为．再由（an+1﹣p）（an﹣p）＜0恒成立求得实数p的取值范围．‎ ‎【解答】解：由，得；‎ 当n≥2时，an=Sn﹣Sn﹣1=‎ ‎=．‎ 若n为偶数，则，∴（n为正奇数）；‎ 若n为奇数，则==，‎ ‎∴（n为正偶数）．‎ 函数（n为正奇数）为减函数，最大值为，‎ 函数（n为正偶数）为增函数，最小值为．‎ 若（an+1﹣p）（an﹣p）＜0恒成立，‎ 则a1＜p＜a2，即．‎ 故答案为：．‎ ‎【点评】本题考查数列递推式，考查了数列通项公式的求法，体现了分类讨论的数学思想方法和数学转化思想方法，是中档题．‎ ‎　‎ 二、选择题（本大题满分20分）本大题共有4题，每题只有一个正确答案.考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．‎ ‎15．若a，b∈R，且ab＞0，则“a=b”是“等号成立”的（　　）‎ A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既非充分又非必要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【专题】定义法；不等式的解法及应用；简易逻辑．‎ ‎【分析】根据充分条件和必要条件的定义结合基本的性质进行判断即可．‎ ‎【解答】解：∵ab＞0，∴＞0，‎ 当a=b，则+=1+1=2，此时等号成立，‎ ‎+≥2=2，当且仅当=，即a=b时取等号，‎ 故“a=b”是“等号成立”的充要条件，‎ 故选：A ‎【点评】本题主要考查充分条件和必要条件的判断，根据基本不等式的性质是解决本题的关键．‎ ‎　‎ ‎16．设f（x）=2+5x+10x2+10x3+5x4+x5，则其反函数的解析式为（　　）‎ A． B． C． D．‎ ‎【考点】反函数．‎ ‎【专题】定义法；函数的性质及应用；二项式定理．‎ ‎【分析】根据二项式定理：（1+x）5=1+5x+10x2+10x3+5x4+x5，原函数可写成y=1+（1+x）5，再求其反函数即可．‎ ‎【解答】解：因为y=f（x）=2+5x+10x2+10x3+5x4+x5‎ ‎=1+[1+5x+10x2+10x3+5x4+x5]=1+（1+x）5，‎ 即y=1+（1+x）5，所以，1+x=，‎ 因此，x=﹣1+，‎ 再交换x，y得，y=﹣1+，‎ 所以，f（x）的反函数的解析式为f﹣1（x）=﹣1+，x∈R，‎ 故答案为：C．‎ ‎【点评】本题主要考查了反函数及其解法，涉及二项式定理的应用，根式的运算和函数定义域与值域的确定，属于中档题．‎ ‎　‎ ‎17．△ABC的内角A，B，C的对边分别为a，b，c，满足，则角A的范围是（　　）‎ A． B． C． D．‎ ‎【考点】余弦定理．‎ ‎【专题】计算题；数形结合；分析法；解三角形．‎ ‎【分析】由已知可得（a﹣b+c）（a+b﹣c）≤bc，整理可得：b2+c2﹣a2≥bc，利用余弦定理可得cosA=≥=，利用余弦函数的图象和性质即可得解A的范围．‎ ‎【解答】解：∵，‎ 又∵由于三角形两边之和大于第三边，可得a+c﹣b＞0，a+b﹣c＞0，且b，c＞0，‎ ‎∴（a﹣b+c）（a+b﹣c）≤bc，整理可得：b2+c2﹣a2≥bc，‎ ‎∴cosA=≥=，‎ ‎∵A∈（0，）．‎ 故选：B．‎ ‎【点评】本题主要考查了余弦定理，余弦函数的图象和性质的综合应用，考查了计算能力和数形结合能力，属于中档题．‎ ‎　‎ ‎18．函数f（x）的定义域为[﹣1，1]，图象如图1所示；函数g（x）的定义域为[﹣1，2]，图象如图2所示．A={x|f（g（x））=0}，B={x|g（f（x））=0}，则A∩B中元素的个数为（　　）‎ A．1 B．2 C．3 D．4‎ ‎【考点】函数的图象；交集及其运算．‎ ‎【专题】数形结合；定义法；函数的性质及应用；集合．‎ ‎【分析】结合图象，分别求出集合A，B，再根据交集的定义求出A∩B，问题得以解决．‎ ‎【解答】解：由图象可知，‎ 若f（g（x））=0，‎ 则g（x）=0或g（x）=1，‎ 由图2知，g（x）=0时，x=0，或x=2，‎ g（x）=1时，x=1或x=﹣1‎ 故A={﹣1，0，1，2}，‎ 若g（f（x））=0，‎ 由图1知，f（x）=0，或f（x）=2（舍去），‎ 当f（x）=0时，x=﹣1或0或1，‎ 故B={﹣1，0，1}，‎ 所以A∩B={﹣1，0，1}，‎ 则A∩B中元素的个数为3个．‎ 故选：C．‎ ‎【点评】本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用，属于中档题．‎ ‎　‎ 三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．‎ ‎19．如图，三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AA1=AB=2，BC=1，，D为棱AA1中点，证明异面直线B1C1与CD所成角为，并求三棱柱ABC﹣A1B1C1的体积．‎ ‎【考点】棱柱、棱锥、棱台的体积．‎ ‎【专题】数形结合；数形结合法；空间位置关系与距离．‎ ‎【分析】在△ABC中使用正弦定理得出∠ACB=90°，即AC⊥BC，又AA1⊥平面ABC得AA1⊥BC，故BC⊥平面ACC1A1，于是BC⊥CD，由BC∥B1C1得出B1C1⊥CD，利用棱柱的体积公式求出棱柱的体积．‎ ‎【解答】证明：在△ABC中，由正弦定理得，即，‎ ‎∴sin∠ACB=1，即，∴BC⊥AC．‎ ‎∵AA1⊥平面ABC，BC⊂平面ABC，‎ ‎∴BC⊥AA1，又AC⊂平面ACC1A1，AA1⊂平面ACC1A1，AA1∩AC=A，‎ ‎∴BC⊥平面平面ACC1A1，CD⊂平面ACC1A1，‎ ‎∴BC⊥CD，∵BC∥B1C1，‎ ‎∴B1C1⊥CD，‎ ‎∴异面直线B1C1与CD所成角为．‎ ‎∵AB=2，BC=1，∠ACB=，‎ ‎∴AC=．‎ ‎∴三棱柱ABC﹣A1B1C1的体积V=S△ABC•AA1==．‎ ‎【点评】本题考查了线面垂直的判定，棱柱的结构特征，棱柱的体积计算，属于中档题．‎ ‎　‎ ‎20．如图，点A、B分别是角α、β的终边与单位圆的交点，．‎ ‎（1）若，，求sin2β的值；‎ ‎（2）证明：cos（α﹣β）=cosαcosβ+sinαsinβ．‎ ‎【考点】两角和与差的余弦函数；任意角的三角函数的定义．‎ ‎【专题】转化思想；综合法；三角函数的求值．‎ ‎【分析】（1）由条件利用二倍角公式，诱导公式，求得sin2β的值．‎ ‎（2）由条件利用两个向量的数量积公式、两个向量的数量积的定义，证得公式成立．‎ ‎【解答】解：（1）由，可得cos（2α﹣2β）=2cos2（α﹣β）﹣1=﹣，‎ ‎∵，∴cos（﹣2β）=﹣，∴sin2β=．‎ ‎（2）由题意可得，||=||=1，且与的夹角为α﹣β， =（cosα，sinα），=（cosβ，sinβ），‎ ‎=cosαcosβ+sinαsinβ=1×1×cos（α﹣β），‎ ‎∴cos（α﹣β）=cosαcosβ+sinαsinβ成立．‎ ‎【点评】本题主要考查二倍角公式，诱导公式的应用，两个向量的数量积的运算，属于中档题．‎ ‎　‎ ‎21．某沿海城市的海边有两条相互垂直的直线型公路l1、l2，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个公共点P（即直线与曲线相切），如图所示．若曲线段MPN是函数图象的一段，点M到l1、l2的距离分别为8千米和1千米，点N到l2的距离为10千米，以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy，设点P的横坐标为p．‎ ‎（1）求曲线段MPN的函数关系式，并指出其定义域；‎ ‎（2）若某人从点O沿公路至点P观景，要使得沿折线OAP比沿折线OBP的路程更近，求p的取值范围．‎ ‎【考点】两点间距离公式的应用；函数解析式的求解及常用方法．‎ ‎【专题】计算题；方程思想；综合法；直线与圆．‎ ‎【分析】（1）由题意得M（1，8），则a=8，故曲线段MPN的函数关系式为，可得其定义域；‎ ‎（2），设与联立求出A，B的坐标，即可求出最短长度p的取值范围．‎ ‎【解答】解：（1）由题意得M（1，8），则a=8，故曲线段MPN的函数关系式为，‎ 又得，所以定义域为[1，10]．…‎ ‎（2），设 由得kpx2+（8﹣kp2）x﹣8p=0，‎ ‎△=（8﹣kp2）2+32kp2=（kp2+8）2=0，…‎ ‎∴kp2+8=0，∴，得直线AB方程为，…‎ 得，故点P为AB线段的中点，‎ 由即p2﹣8＞0…‎ 得时，OA＜OB，‎ 所以，当时，经点A至P路程最近．‎ ‎【点评】本题考查利用数学知识解决实际问题，考查学生分析解决问题的能力，确定函数关系是关键．‎ ‎　‎ ‎22．已知椭圆Γ的中心在坐标原点，且经过点，它的一个焦点与抛物线 E：y2=4x的焦点重合．‎ ‎（1）求椭圆Γ的方程；‎ ‎（2）斜率为k的直线l过点F（1，0），且与抛物线 E交于A、B两点，设点P（﹣1，k），△PAB的面积为，求k的值；‎ ‎（3）若直线l过点M（0，m）（m≠0），且与椭圆Γ交于C、D两点，点C关于y轴的对称点为Q，直线QD的纵截距为n，证明：mn为定值．‎ ‎【考点】椭圆的简单性质．‎ ‎【专题】数形结合；方程思想；转化思想；圆锥曲线的定义、性质与方程．‎ ‎【分析】（1）设椭圆的方程为，由题设得，解出即可得出．‎ ‎（2）设直线l：y=k（x﹣1），与椭圆方程联立可得k2x2﹣2（k2+2）x+k2=0，l与抛物线 E有两个交点，k≠0，△＞0，利用根与系数的关系可得|AB|，P（﹣1，k）到l的距离，又，解出即可得出．‎ ‎（3）由C（x1，y1），D（x2，y2），点C关于y轴的对称点为Q（﹣x1，y1），则直线，设x=0得m；直线，设x=0得n，再利用根与系数的关系即可得出．‎ ‎【解答】解：（1）设椭圆的方程为，由题设得，‎ ‎∴，‎ ‎∴椭圆Γ的方程是．‎ ‎（2）设直线l：y=k（x﹣1），由，得k2x2﹣2（k2+2）x+k2=0，‎ l与抛物线 E有两个交点，k≠0，△=16（k2+1）＞0，‎ 则，‎ P（﹣1，k）到l的距离，又，‎ ‎∴，‎ ‎∴4k2=3k2+3，故． ‎ ‎（3）∵C（x1，y1），D（x2，y2），点C关于y轴的对称点为Q（﹣x1，y1），‎ 则直线，设x=0得 直线，设x=0得，‎ ‎∴，又，，‎ ‎∴，，‎ ‎∴．‎ ‎【点评】本题考查了椭圆的定义及其标准方程、直线与椭圆相交弦长问题、点到直线的距离公式、三角形面积计算公式、轴对称问题、两点之间的距离公式，考查了推理能力与计算能力，属于难题．‎ ‎　‎ ‎23．已知数列{an}的各项均为整数，其前n项和为Sn．规定：若数列{an}满足前r项依次成公差为1的等差数列，从第r﹣1项起往后依次成公比为2的等比数列，则称数列{an}为“r关联数列”．‎ ‎（1）若数列{an}为“6关联数列”，求数列{an}的通项公式；‎ ‎（2）在（1）的条件下，求出Sn，并证明：对任意n∈N*，anSn≥a6S6；‎ ‎（3）已知数列{an}为“r关联数列”，且a1=﹣10，是否存在正整数k，m（m＞k），使得a1+a2+…+ak﹣1+ak=a1+a2+…+am﹣1+am？若存在，求出所有的k，m值；若不存在，请说明理由．‎ ‎【考点】数列的应用．‎ ‎【专题】综合题；转化思想；综合法；等差数列与等比数列．‎ ‎【分析】（1）若数列{an}为“6关联数列”，{an}前6项为等差数列，从第5项起为等比数列，可得a6=a1+5，a5=a1+4，且，即，解得a1，即可求数列{an}的通项公式；‎ ‎（2）由（1）得（或，可见数列{anSn}的最小项为a6S6=﹣6，即可证明：对任意n∈N*，anSn≥a6S6；‎ ‎（3），分类讨论，求出所有的k，m值．‎ ‎【解答】解：（1）∵数列{an}为“6关联数列”，‎ ‎∴{an}前6项为等差数列，从第5项起为等比数列，‎ ‎∴a6=a1+5，a5=a1+4，且，即，解得a1=﹣3…‎ ‎∴（或）． …‎ ‎（2）由（1）得（或）…‎ ‎，‎ ‎{Sn}：﹣3，﹣5，﹣6，﹣6，﹣5，﹣3，1，9，25，…{anSn}：9，10，6，0，﹣5，﹣6，4，72，400，…，‎ 可见数列{anSn}的最小项为a6S6=﹣6，‎ 证明：，‎ 列举法知当n≤5时，（anSn）min=a5S5=﹣5； …‎ 当n≥6时，，设t=2n﹣5，则． …‎ ‎（3）数列{an}为“r关联数列”，且a1=﹣10，∵‎ ‎∴…‎ ‎①当k＜m≤12时，由得（k+m）（k﹣m）=21（k﹣m）k+m=21，k，m≤12，m＞k，∴或．‎ ‎②当m＞k＞12时，由2k﹣11﹣56=2m﹣11﹣56得m=k，不存在 …‎ ‎③当k≤12，m＞12时，由，2m﹣10=k2﹣21k+112‎ 当k=1时，2m﹣10=92，m∉N*；当k=2时，2m﹣10=74，m∉N*；‎ 当k=3时，2m﹣10=58，m∉N*；当k=4时，2m﹣10=44，m∉N*；‎ 当k=5时，2m﹣10=25，m=15∈N*；当k=6时，2m﹣10=22，m∉N*；‎ 当k=7时，2m﹣10=14，m∉N*；当k=8时，2m﹣10=23，m=13∈N*；‎ 当k=9时，2m﹣10=22，m=12舍去；当k=10时，2m﹣10=2，m=11舍去 当k=11时，2m﹣10=2，m=11舍去；当k=12时，2m﹣10=22，m=12舍去…‎ 综上所述，∴存在或或或． …‎ ‎【点评】本题考查数列的应用，考查新定义，考查数列的通项，考查分类讨论的数学思想，难度大．‎ ‎　‎