高考球的内切和外接常考类型全归纳 4页

‎ 多面体与球的内切和外接常见类型归纳 在平常教学中，立体几何的多面体与球的位置关系，是培养学生的立体感，空间想象能力的好教材。可是学生在两个几何体的组合后，往往感到无从下手。针对这种情况，笔者把日常教学中有关这方面的习题加以总结和归类如下：‎ 一．正四面体与球C B D A O S E F 如图所示，设正四面体的棱长为a，r为内切球的半径，R为外接球的半径。则高SE=a,斜高SD=a，OE=r=SE-SO，又SD=BD,BD=SE-OE,则在 ‎ r=。R=SO=OB=‎ 特征分析：‎ 1． 由于正四面体是一个中心对成图形，所以它的内切球与外接球的球心为同一个。‎ 2． R=3r. r= R=。此结论可以记忆。‎ 例题一。1、一个四面体的所有棱长都为，四个顶点在同一球面上，则此球的表面积为（ ）‎ 分析：借助结论，R===,所以S=4=3。‎ ‎2、球的内接正四面体又有一个内切球，则大球与小球的表面积之比是（ ）‎ 分析：借助R=3r，答案为9：1。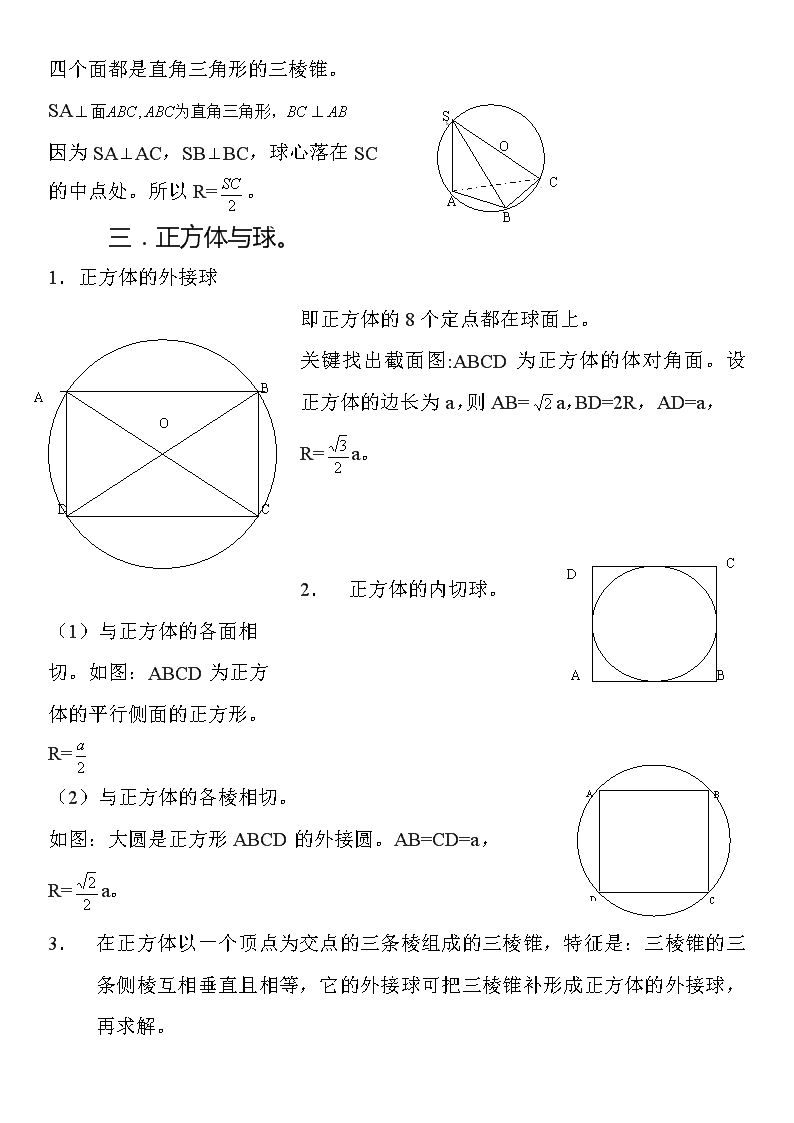‎ 二、特殊三棱锥与球 S A C O B O C B A S 四个面都是直角三角形的三棱锥。‎ SA 因为SAAC，SBBC，球心落在SC 的中点处。所以R=。‎ 三．正方体与球。‎ ‎1．正方体的外接球 即正方体的8个定点都在球面上。‎ A O B D C 关键找出截面图:ABCD为正方体的体对角面。设正方体的边长为a，则AB=a，BD=2R，AD=a，‎ R=a。‎ C D A 2． 正方体的内切球。‎ ‎（1）与正方体的各面相 B 切。如图：ABCD为正方 体的平行侧面的正方形。‎ A D B C R=‎ ‎（2）与正方体的各棱相切。 ‎ 如图：大圆是正方形ABCD的外接圆。AB=CD=a，‎ R=a。‎ 3． 在正方体以一个顶点为交点的三条棱组成的三棱锥，特征是：三棱锥的三条侧棱互相垂直且相等，它的外接球可把三棱锥补形成正方体的外接球，再求解。‎ 例题：1。正方体的全面积是24，它的顶点都在同一球面上，这个球的表面积是 ‎ 解析：显然，球是正方体的外接球，a=2，则R=，S=12。‎ ‎2．一个球与棱长为1 的正方体的12条棱都相切，则球的体积 ‎ 解析：如果明确了上面的结论，问题很容易解决。R==1==‎ V=‎ ‎3．将棱长为1 的正方体削成体积最大的球，则球的体积为 ‎ 解析：削成体积最大，即要求球是正方体的内切球，与正方体的俄各面都相切。R=，V=。‎ ‎4．P、A、B、C、是球O面上的四个点，PA、PB、PC两两垂直，且PA=PB=PC=1，则球的体积是 ‎ 解析：同过条件分析，可采用把三棱锥补形成正方体，则球是正方体的外接球，所以R=，V=。‎ B A C C1‎ A11‎ B1‎ D11‎ D O 四、正棱柱与球 ‎ ‎1．正三棱柱外接球。‎ 如图所示：过A点作AD垂直BC,D为三角形ABC的中心，D1同样得到。则球心O必落在DD1的中点上。利用三角形OAD为直角三角形，OA=R,可求出R.‎ ‎2.正四棱柱外接球。‎ 道理与上面相似。主要是找截面，构造直角三角形，利用勾股定理求得。‎ 例题：1。已知一个半径为的球中有一个各条棱长都相等的内接正三棱柱，则这一正三棱柱的体积是 ‎ C B A D O 解析：如上图，OA=,OD=，AD=，可求a＝6，V=54.‎ ‎2. 正四棱柱ABCD-A1B1C1D1的各个顶点都在半径为R的球面上，则正四棱柱的侧面积有最 值，为 ‎ 解析：截面如图：ABCD为正四棱柱的体对角面OD=R，设AD=a，底面正方形的边长为b，则有DC=b，则R2=（a/2）2+（b/2）2，S=4ba=。‎ 五、长方体与球 C B A D O ‎1．长方体的外接球。‎ 截面图如右图：实质构造直角三角形，联系半径与长方体的长宽高。半径为体对角线的一半。‎ ‎2．在长方体以一个顶点为交点的三条棱组成的三棱锥，特征是：三棱锥的三条侧棱互相垂直不相等，它的外接球可把三棱锥补形成长方体的外接球，再求解。‎ 例题：一个三棱锥三条棱两两垂直，其长分别是3，4，5，则它的外接球的表面积是 ‎ 解析：同过条件分析，可采用把三棱锥补形成长方体，则球是长方体的外接球，所以R=，S=50。‎