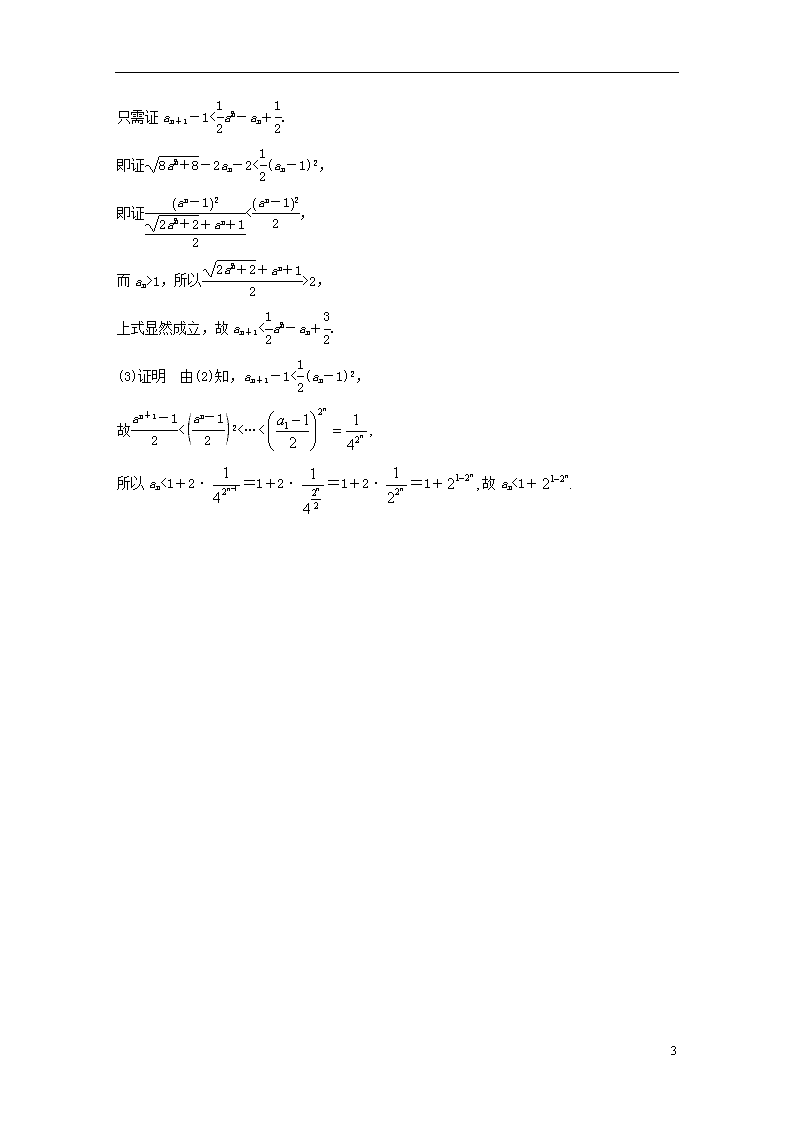- 48.00 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
规范答题示例5 数列的通项与求和问题
典例5 (15分)已知数列{an}中,a1=4,an+1=,n∈N*,Sn为{an}的前n项和.
(1)求证:当n∈N*时,an>an+1;
(2)求证:当n∈N*时,2≤Sn-2n<.
审题路线图 (1)
(2)―→―→
―→
―→
规 范 解 答·分 步 得 分
构 建 答 题 模 板
证明 (1)当n≥2时,
因为an-an+1=-=,2分
所以an-an+1与an-1-an同号.3分
又因为a1=4,a2=,a1-a2>0,
所以当n∈N*时,an>an+1.5分
(2)由条件易得2a=6+an,所以2(a-4)=an-2,
所以2(an+1-2)(an+1+2)=an-2,①
所以an+1-2与an-2同号.
又因为a1=4,即a1-2>0,所以an>2.8分
又Sn=a1+a2+…+an≥a1+(n-1)×2=2n+2.
所以Sn-2n≥2.10分
由①可得=<,因此an-2≤(a1-2)×
第一步
找关系:分析数列的递推式,把握数列的项之间的关系;
第二步
巧变形:根据所证式子的特点,对递推式灵活变形或适当放缩;
第三步
凑结论:观察变形后的式子和欲证结论的联系,凑出最后结果.
3
n-1,
即an≤2+2×n-1,12分
所以Sn=a1+a2+…+an≤2n+2
=2n+<2n+.
综上可得,2≤Sn-2n<.15分
评分细则 (1)证出an-an+1与an-1-an同号给3分.
(2)证出an+1-2与an-2同号给2分.
(3)证出Sn-2n≥2给2分.
跟踪演练5 (2018·温州高考适应性测试)已知正项数列{an}满足an+1=-2an-1,且an+10,
解得an>1或an<-7(舍去),
所以a1>1.
(2)证明 方法一 要证明an+10,
因为an>1,上式显然成立,故an+11,所以>2,
上式显然成立,故an+1
相关文档
- 2013高中生物浙科版必修1单元检测 2021-05-136页
- 2020版高中数学 第一章 统计 12021-05-134页
- 精华经典版122页高考数学知识点总2021-05-13168页
- 江苏2019普通高中学业水平测试小高2021-05-1311页
- 高中历史高考真题题汇编2021-05-134页
- 全国八省联考2021年湖北省普通高中2021-05-1318页
- 全国八省联考河北省2021年1月普通2021-05-1332页
- 全国八省联考2021年1月重庆市普通2021-05-1328页
- 高考:高中地理23个简答题答题规范2021-05-1324页
- 全国八省联考2021年1月湖北省普通2021-05-1331页