上海市春季高考数学试卷解析 22页

‎2016年上海市春季高考数学试卷 ‎　‎ 一.填空题（本大题共12题，每题3分，共36分）‎ ‎1．复数3+4i（i为虚数单位）的实部是　　　　　　．‎ ‎2．若log2（x+1）=3，则x=　　　　　　．‎ ‎3．直线y=x﹣1与直线y=2的夹角为　　　　　　．‎ ‎4．函数的定义域为　　　　　　．‎ ‎5．三阶行列式中，元素5的代数余子式的值为　　　　　　．‎ ‎6．函数的反函数的图象经过点（2，1），则实数a=　　　　　　．‎ ‎7．在△ABC中，若A=30°，B=45°，，则AC=　　　　　　．‎ ‎8．4个人排成一排照相，不同排列方式的种数为　　　　　　（结果用数值表示）．‎ ‎9．无穷等比数列{an}的首项为2，公比为，则{an}的各项的和为　　　　　　．‎ ‎10．若2+i（i为虚数单位）是关于x的实系数一元二次方程x2+ax+5=0的一个虚根，则a=　　　　　　．‎ ‎11．函数y=x2﹣2x+1在区间[0，m]上的最小值为0，最大值为1，则实数m的取值范围是　　　　　　．‎ ‎12．在平面直角坐标系xOy中，点A，B是圆x2+y2﹣6x+5=0上的两个动点，且满足，则的最小值为　　　　　　．‎ ‎　‎ 二.选择题（本大题共12题，每题3分，共36分）‎ ‎13．若sinα＞0，且tanα＜0，则角α的终边位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎14．半径为1的球的表面积为（　　）‎ A．π B． C．2π D．4π ‎15．在（1+x）6的二项展开式中，x2项的系数为（　　）‎ A．2 B．6 C．15 D．20‎ ‎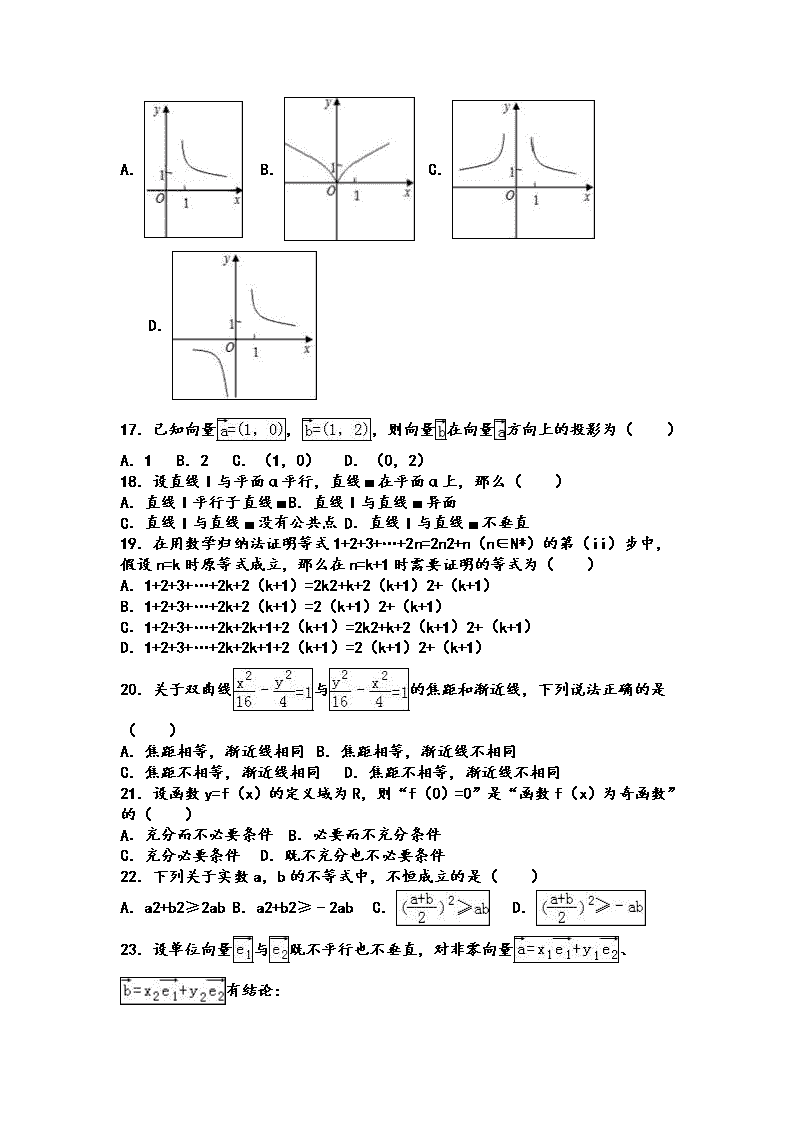16．幂函数y=x﹣2的大致图象是（　　）‎ A． B． C． D．‎ ‎17．已知向量，，则向量在向量方向上的投影为（　　）‎ A．1 B．2 C．（1，0） D．（0，2）‎ ‎18．设直线l与平面α平行，直线m在平面α上，那么（　　）‎ A．直线l平行于直线m B．直线l与直线m异面 C．直线l与直线m没有公共点 D．直线l与直线m不垂直 ‎19．在用数学归纳法证明等式1+2+3+…+2n=2n2+n（n∈N*）的第（ii）步中，假设n=k时原等式成立，那么在n=k+1时需要证明的等式为（　　）‎ A．1+2+3+…+2k+2（k+1）=2k2+k+2（k+1）2+（k+1）‎ B．1+2+3+…+2k+2（k+1）=2（k+1）2+（k+1）‎ C．1+2+3+…+2k+2k+1+2（k+1）=2k2+k+2（k+1）2+（k+1）‎ D．1+2+3+…+2k+2k+1+2（k+1）=2（k+1）2+（k+1）‎ ‎20．关于双曲线与的焦距和渐近线，下列说法正确的是（　　）‎ A．焦距相等，渐近线相同 B．焦距相等，渐近线不相同 C．焦距不相等，渐近线相同 D．焦距不相等，渐近线不相同 ‎21．设函数y=f（x）的定义域为R，则“f（0）=0”是“函数f（x）为奇函数”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎22．下列关于实数a，b的不等式中，不恒成立的是（　　）‎ A．a2+b2≥2ab B．a2+b2≥﹣2ab C． D．‎ ‎23．设单位向量与既不平行也不垂直，对非零向量、有结论：‎ ‎①若x1y2﹣x2y1=0，则；‎ ‎②若x1x2+y1y2=0，则．‎ 关于以上两个结论，正确的判断是（　　）‎ A．①成立，②不成立 B．①不成立，②成立 C．①成立，②成立 D．①不成立，②不成立 ‎24．对于椭圆．若点（x0，y0）满足．则称该点在椭圆C（a，b）内，在平面直角坐标系中，若点A在过点（2，1）的任意椭圆C（a，b）内或椭圆C（a，b）上，则满足条件的点A构成的图形为（　　）‎ A．三角形及其内部 B．矩形及其内部 C．圆及其内部 D．椭圆及其内部 ‎　‎ 三.解答题（本大题共5题，共8+8+8+12+12=48分）‎ ‎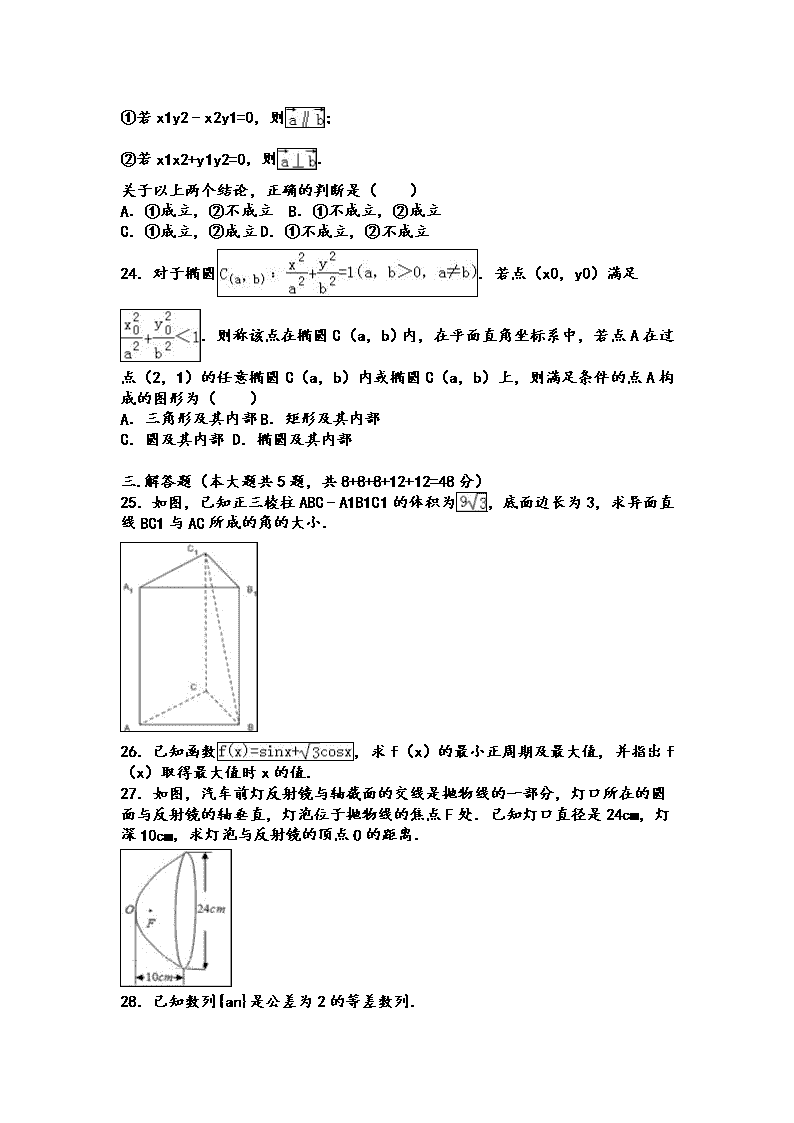25．如图，已知正三棱柱ABC﹣A1B1C1的体积为，底面边长为3，求异面直线BC1与AC所成的角的大小．‎ ‎26．已知函数，求f（x）的最小正周期及最大值，并指出f（x）取得最大值时x的值．‎ ‎27．如图，汽车前灯反射镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反射镜的轴垂直，灯泡位于抛物线的焦点F处．已知灯口直径是24cm，灯深10cm，求灯泡与反射镜的顶点O的距离．‎ ‎28．已知数列{an}是公差为2的等差数列．‎ ‎（1）a1，a3，a4成等比数列，求a1的值；‎ ‎（2）设a1=﹣19，数列{an}的前n项和为Sn．数列{bn}满足，记（n∈N*），求数列{cn}的最小项（即对任意n∈N*成立）．‎ ‎29．对于函数f（x），g（x），记集合Df＞g={x|f（x）＞g（x）}．‎ ‎（1）设f（x）=2|x|，g（x）=x+3，求Df＞g；‎ ‎（2）设f1（x）=x﹣1，，h（x）=0，如果．求实数a的取值范围．‎ ‎　‎ 二卷一.选择题：‎ ‎30．若函数f（x）=sin（x+φ）是偶函数，则ϕ的一个值是（　　）‎ A．0 B． C．π D．2π ‎31．在复平面上，满足|z﹣1|=4的复数z的所对应的轨迹是（　　）‎ A．两个点 B．一条线段 C．两条直线 D．一个圆 ‎32．已知函数y=f（x）的图象是折线ABCDE，如图，其中A（1，2），B（2，1），C（3，2），D（4，1），E（5，2），若直线y=kx+b与y=f（x）的图象恰有四个不同的公共点，则k的取值范围是（　　）‎ A．（﹣1，0）∪（0，1） B． C．（0，1] D．‎ ‎　‎ 二.填空题：‎ ‎33．椭圆的长半轴的长为　　　　　　．‎ ‎34．已知圆锥的母线长为10，母线与轴的夹角为30°，则该圆锥的侧面积为　　　　　　．‎ ‎35．小明用数列{an}记录某地区2015年12月份31天中每天是否下过雨，方法为：当第k天下过雨时，记ak=1，当第k天没下过雨时，记ak=﹣1（1≤k≤31），他用数列{bn}记录该地区该月每天气象台预报是否有雨，方法为：当预报第k天有雨时，记bn=1，当预报第k天没有雨时，记bn=﹣1记录完毕后，小明计算出a1b1+a2b2+a3b3+…+a31b31=25，那么该月气象台预报准确的总天数为　　　　　　．‎ ‎　‎ 三.解答题：‎ ‎36．对于数列{an}与{bn}，若对数列{cn}的每一项cn，均有ck=ak或ck=bk，则称数列{cn}是{an}与{bn}的一个“并数列”．‎ ‎（1）设数列{an}与{bn}的前三项分别为a1=1，a2=3，a3=5，b1=1，b2=2，b3=3，若{cn}是{an}与{bn}一个“并数列”求所有可能的有序数组（c1，c2，c3）；‎ ‎（2）已知数列{an}，{cn}均为等差数列，{an}的公差为1，首项为正整数t；{cn}的前10项和为﹣30，前20项的和为﹣260，若存在唯一的数列{bn}，使得{cn}是{an}与{bn}的一个“并数列”，求t的值所构成的集合．‎ ‎　‎ ‎2016年上海市春季高考数学试卷 参考答案与试题解析 ‎　‎ 一.填空题（本大题共12题，每题3分，共36分）‎ ‎1．复数3+4i（i为虚数单位）的实部是　3　．‎ ‎【考点】复数的基本概念．‎ ‎【分析】根据复数的定义判断即可．‎ ‎【解答】解：复数3+4i（i为虚数单位）的实部是3，‎ 故答案为：3．‎ ‎　‎ ‎2．若log2（x+1）=3，则x=　7　．‎ ‎【考点】对数的运算性质；函数的零点．‎ ‎【分析】直接利用对数运算法则化简求解即可．‎ ‎【解答】解：log2（x+1）=3，可得x+1=8，解得x=7．‎ 故答案为：7．‎ ‎　‎ ‎3．直线y=x﹣1与直线y=2的夹角为　　．‎ ‎【考点】两直线的夹角与到角问题．‎ ‎【分析】由题意可得直线的斜率，可得倾斜角，进而可得直线的夹角．‎ ‎【解答】解：∵直线y=x﹣1的斜率为1，故倾斜角为，‎ 又∵直线y=2的倾斜角为0，‎ 故直线y=x﹣1与直线y=2的夹角为，‎ 故答案为：．‎ ‎　‎ ‎4．函数的定义域为　[2，+∞）　．‎ ‎【考点】函数的定义域及其求法．‎ ‎【分析】直接由根式内部的代数式大于等于0求解即可．‎ ‎【解答】解：由x﹣2≥0得，x≥2．‎ ‎∴原函数的定义域为[2，+∞）．‎ 故答案为[2，+∞）．‎ ‎　‎ ‎5．三阶行列式中，元素5的代数余子式的值为　8　．‎ ‎【考点】高阶矩阵．‎ ‎【分析】根据余子式的定义可知，在行列式中划去第1行第3列后所余下的2阶行列式带上符号（﹣1）i+j，求出其表达式的值即可．‎ ‎【解答】解：元素5的代数余子式为：（﹣1）1+3||=（4×2+1×0）=8．‎ ‎∴元素5的代数余子式的值为8．‎ 故答案为：8．‎ ‎　‎ ‎6．函数的反函数的图象经过点（2，1），则实数a=　1　．‎ ‎【考点】反函数．‎ ‎【分析】由于函数的反函数的图象经过点（2，1），可得函数的图象经过点（1，2），即可得出．‎ ‎【解答】解：∵函数的反函数的图象经过点（2，1），‎ ‎∴函数的图象经过点（1，2），‎ ‎∴2=+a，解得a=1．‎ 故答案为：1．‎ ‎　‎ ‎7．在△ABC中，若A=30°，B=45°，，则AC=　　．‎ ‎【考点】余弦定理；正弦定理．‎ ‎【分析】利用正弦定理即可计算求解．‎ ‎【解答】解：∵A=30°，B=45°，，‎ ‎∴由正弦定理，可得：AC===2．‎ 故答案为：2．‎ ‎　‎ ‎8．4个人排成一排照相，不同排列方式的种数为　24　（结果用数值表示）．‎ ‎【考点】计数原理的应用．‎ ‎【分析】根据题意，由排列数公式直接计算即可．‎ ‎【解答】解：4个人排成一排照相，不同排列方式的种数为A44=24种，‎ 故答案为：24．‎ ‎　‎ ‎9．无穷等比数列{an}的首项为2，公比为，则{an}的各项的和为　3　．‎ ‎【考点】等比数列的前n项和．‎ ‎【分析】{an}的各项的和=，即可得出．‎ ‎【解答】解：{an}的各项的和为： ==3．‎ 故答案为：3．‎ ‎　‎ ‎10．若2+i（i为虚数单位）是关于x的实系数一元二次方程x2+ax+5=0的一个虚根，则a=　﹣4　．‎ ‎【考点】复数代数形式的混合运算．‎ ‎【分析】2+i（i为虚数单位）是关于x的实系数一元二次方程x2+ax+5=0的一个虚根，则2﹣i（i为虚数单位）也是关于x的实系数一元二次方程x2+ax+5=0的一个虚根，再利用根与系数的关系即可得出．‎ ‎【解答】解：∵2+i（i为虚数单位）是关于x的实系数一元二次方程x2+ax+5=0的一个虚根，‎ ‎∴2﹣i（i为虚数单位）也是关于x的实系数一元二次方程x2+ax+5=0的一个虚根，‎ ‎∴2+i+（2﹣i）=﹣a，‎ 解得a=﹣4．‎ 则a=﹣4．‎ 故答案为：﹣4．‎ ‎　‎ ‎11．函数y=x2﹣2x+1在区间[0，m]上的最小值为0，最大值为1，则实数m的取值范围是　[1，2]　．‎ ‎【考点】二次函数在闭区间上的最值．‎ ‎【分析】根据二次函数的性质得出，求解即可．‎ ‎【解答】解：∵f（x）=x2﹣2x+1=（x﹣1）2，‎ ‎∴对称轴x=1，‎ ‎∴f（1）=0，‎ f（2）=1，f（0）=1，‎ ‎∵f（x）=x2﹣2x+2在区间[0，m]上的最大值为1，最小值为0，‎ ‎∴，‎ ‎∴1≤m≤2，‎ 故答案为：1≤m≤2．‎ ‎　‎ ‎12．在平面直角坐标系xOy中，点A，B是圆x2+y2﹣6x+5=0上的两个动点，且满足，则的最小值为　4　．‎ ‎【考点】直线与圆的位置关系；向量的三角形法则．‎ ‎【分析】本题可利用AB中点M去研究，先通过坐标关系，将转化为，用根据AB=2，得到M点的轨迹，由图形的几何特征，求出模的最小值，得到本题答案．‎ ‎【解答】解：设A（x1，y1），B（x2，y2），AB中点M（x′，y′）．‎ ‎∵x′=，y′=，‎ ‎∴=（x1+x2，y1+y2）=2，‎ ‎∵圆C：x2+y2﹣6x+5=0，‎ ‎∴（x﹣3）2+y2=4，圆心C（3，0），半径CA=2．‎ ‎∵点A，B在圆C上，AB=2，‎ ‎∴CA2﹣CM2=（AB）2，‎ 即CM=1．‎ 点M在以C为圆心，半径r=1的圆上．‎ ‎∴OM≥OC﹣r=3﹣1=2．‎ ‎∴||≥2，∴≥4，‎ ‎∴的最小值为4．‎ 故答案为：4．‎ ‎　‎ 二.选择题（本大题共12题，每题3分，共36分）‎ ‎13．若sinα＞0，且tanα＜0，则角α的终边位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【考点】象限角、轴线角．‎ ‎【分析】由sinα＞0，则角α的终边位于一二象限，由tanα＜0，则角α的终边位于二四象限，两者结合即可解决问题．‎ ‎【解答】解：∵sinα＞0，则角α的终边位于一二象限，‎ ‎∵由tanα＜0，‎ ‎∴角α的终边位于二四象限，‎ ‎∴角α的终边位于第二象限．‎ 故选择B．‎ ‎　‎ ‎14．半径为1的球的表面积为（　　）‎ A．π B． C．2π D．4π ‎【考点】球的体积和表面积．‎ ‎【分析】利用球的表面积公式S=4πR2解答即可求得答案．‎ ‎【解答】解：半径为1的球的表面积为4π×12=4π，‎ 故选：D．‎ ‎　‎ ‎15．在（1+x）6的二项展开式中，x2项的系数为（　　）‎ A．2 B．6 C．15 D．20‎ ‎【考点】二项式系数的性质．‎ ‎【分析】根据二项展开式的通项公式求出展开式的特定项即可．‎ ‎【解答】解：（1+x）6的二项展开式中，通项公式为：‎ Tr+1=•16﹣r•xr，‎ 令r=2，得展开式中x2的系数为：‎ ‎=15．‎ 故选：C．‎ ‎　‎ ‎16．幂函数y=x﹣2的大致图象是（　　）‎ A． B． C． D．‎ ‎【考点】函数的图象．‎ ‎【分析】利用负指数幂的定义转换函数，根据函数定义域，利用排除法得出选项．‎ ‎【解答】解：幂函数y=x﹣2=，定义域为（﹣∞，0）∪（0，+∞），‎ 可排除A，B；‎ 值域为（0，+∞）可排除D，‎ 故选：C．‎ ‎　‎ ‎17．已知向量，，则向量在向量方向上的投影为（　　）‎ A．1 B．2 C．（1，0） D．（0，2）‎ ‎【考点】平面向量数量积的运算．‎ ‎【分析】求出，代入向量的投影公式计算．‎ ‎【解答】解： =1， =1，||=，‎ ‎∴向量在向量方向上的投影=1．‎ 故选：A．‎ ‎　‎ ‎18．设直线l与平面α平行，直线m在平面α上，那么（　　）‎ A．直线l平行于直线m B．直线l与直线m异面 C．直线l与直线m没有公共点 D．直线l与直线m不垂直 ‎【考点】空间中直线与直线之间的位置关系．‎ ‎【分析】由已知中直线l与平面α平行，直线m在平面α上，可得直线l与直线m异面或平行，进而得到答案．‎ ‎【解答】解：∵直线l与平面α平行，直线m在平面α上，‎ ‎∴直线l与直线m异面或平行，‎ 即直线l与直线m没有公共点，‎ 故选：C．‎ ‎　‎ ‎19．在用数学归纳法证明等式1+2+3+…+2n=2n2+n（n∈N*）的第（ii）步中，假设n=k时原等式成立，那么在n=k+1时需要证明的等式为（　　）‎ A．1+2+3+…+2k+2（k+1）=2k2+k+2（k+1）2+（k+1）‎ B．1+2+3+…+2k+2（k+1）=2（k+1）2+（k+1）‎ C．1+2+3+…+2k+2k+1+2（k+1）=2k2+k+2（k+1）2+（k+1）‎ D．1+2+3+…+2k+2k+1+2（k+1）=2（k+1）2+（k+1）‎ ‎【考点】数学归纳法．‎ ‎【分析】由数学归纳法可知n=k时，1+2+3+…+2k=2k2+k，到n=k+1时，左端为1+2+3+…+2k+2k+1+2（k+1），从而可得答案．‎ ‎【解答】解：∵用数学归纳法证明等式1+2+3+…+2n=2n2+n时，‎ 当n=1左边所得的项是1+2；‎ 假设n=k时，命题成立，1+2+3+…+2k=2k2+k，‎ 则当n=k+1时，左端为1+2+3+…+2k+2k+1+2（k+1），‎ ‎∴从“k→k+1”需增添的项是2k+1+2（k+1），‎ ‎∴1+2+3+…+2k+2k+1+2（k+1）=2（k+1）2+（k+1）．‎ 故选：D．‎ ‎　‎ ‎20．关于双曲线与的焦距和渐近线，下列说法正确的是（　　）‎ A．焦距相等，渐近线相同 B．焦距相等，渐近线不相同 C．焦距不相等，渐近线相同 D．焦距不相等，渐近线不相同 ‎【考点】双曲线的简单性质．‎ ‎【分析】分别求得双曲线的焦点的位置，求得焦点坐标和渐近线方程，即可判断它们焦距相等，但渐近线不同．‎ ‎【解答】解：双曲线的焦点在x轴上，‎ 可得焦点为（±，0），即为（±2，0），‎ 渐近线方程为y=±x；‎ 的焦点在y轴上，‎ 可得焦点为（0，±2），渐近线方程为y=±2x．‎ 可得两双曲线具有相等的焦距，但渐近线不同．‎ 故选：B．‎ ‎　‎ ‎21．设函数y=f（x）的定义域为R，则“f（0）=0”是“函数f（x）为奇函数”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】函数y=f（x）的定义域为R，若函数f（x）为奇函数，则f（0）=0，反之不成立，例如f（x）=x2．即可判断出结论．‎ ‎【解答】解：函数y=f（x）的定义域为R，若函数f（x）为奇函数，则f（0）=0，反之不成立，例如f（x）=x2．‎ ‎∴“f（0）=0”是“函数f（x）为奇函数”的必要不充分条件．‎ 故选：B．‎ ‎　‎ ‎22．下列关于实数a，b的不等式中，不恒成立的是（　　）‎ A．a2+b2≥2ab B．a2+b2≥﹣2ab C． D．‎ ‎【考点】不等式的基本性质．‎ ‎【分析】根据级别不等式的性质分别判断即可．‎ ‎【解答】解：对于A：a2+b2﹣2ab=（a﹣b）2≥0，故A恒成立；‎ 对于B：a2+b2+2ab=（a+b）2≥0，故B恒成立；‎ 对于C：﹣ab=≥0，故C恒成立；D不恒成立；‎ 故选：D．‎ ‎　‎ ‎23．设单位向量与既不平行也不垂直，对非零向量、有结论：‎ ‎①若x1y2﹣x2y1=0，则；‎ ‎②若x1x2+y1y2=0，则．‎ 关于以上两个结论，正确的判断是（　　）‎ A．①成立，②不成立 B．①不成立，②成立 C．①成立，②成立 D．①不成立，②不成立 ‎【考点】向量的线性运算性质及几何意义．‎ ‎【分析】①假设存在实数λ使得=，则=λ，由于向量与既不平行也不垂直，可得x1=λx2，y1=λy2，即可判断出结论．‎ ‎②若x1x2+y1y2=0，则=（）•=x1x2+y1y2+（x2y1+x1y2）=（x2y1+x1y2），无法得到=0，因此不一定正确．‎ ‎【解答】解：①假设存在实数λ使得=，则=λ，∵向量与既不平行也不垂直，∴x1=λx2，y1=λy2，‎ 满足x1y2﹣x2y1=0，因此．‎ ‎②若x1x2+y1y2=0，‎ 则=（）•=x1x2+y1y2+（x2y1+x1y2）=（x2y1+x1y2），无法得到=0，因此不一定正确．‎ 故选：A．‎ ‎　‎ ‎24．对于椭圆．若点（x0，y0）满足．则称该点在椭圆C（a，b）内，在平面直角坐标系中，若点A在过点（2，1）的任意椭圆C（a，b）内或椭圆C（a，b）上，则满足条件的点A构成的图形为（　　）‎ A．三角形及其内部 B．矩形及其内部 C．圆及其内部 D．椭圆及其内部 ‎【考点】椭圆的简单性质．‎ ‎【分析】点A（x0，y0）在过点P（2，1）的任意椭圆C（a，b）内或椭圆C（a，b）上，可得=1， +≤1．由椭圆的对称性可知：点B（﹣2，1），点C（﹣2，﹣1），点D（2，﹣1），都在任意椭圆上，即可得出．‎ ‎【解答】解：设点A（x0，y0）在过点P（2，1）的任意椭圆C（a，b）内或椭圆C（a，b）上，‎ 则=1， +≤1．‎ ‎∴+≤=1，‎ 由椭圆的对称性可知：点B（﹣2，1），点C（﹣2，﹣1），点D（2，﹣1），都在任意椭圆上，‎ 可知：满足条件的点A构成的图形为矩形PBCD及其内部．‎ 故选：B．‎ ‎　‎ 三.解答题（本大题共5题，共8+8+8+12+12=48分）‎ ‎25．如图，已知正三棱柱ABC﹣A1B1C1的体积为，底面边长为3，求异面直线BC1与AC所成的角的大小．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】由正三棱柱ABC﹣A1B1C1的体积求出高，由A1C1与AC平行，得∠BC1A1是异面直线BC1与AC所成的角，由此利用余弦定理能求出异面直线BC1与AC所成的角的大小．‎ ‎【解答】解：∵正三棱柱ABC﹣A1B1C1的体积为，底面边长为3，‎ ‎∴，解得h=4，‎ ‎∵A1C1与AC平行，∴∠BC1A1是异面直线BC1与AC所成的角，‎ 在△A1BC1中，A1C1=3，BC1=BA1=5，‎ ‎∴cos∠BC1A1==．‎ ‎∴∠BC1A1=arccos．‎ ‎∴异面直线BC1与AC所成的角的大小为arccos．‎ ‎　‎ ‎26．已知函数，求f（x）的最小正周期及最大值，并指出f（x）取得最大值时x的值．‎ ‎【考点】两角和与差的正弦函数；正弦函数的图象．‎ ‎【分析】由条件利用两角和的正弦公式化简f（x）的解析式，再利用正弦函数的周期性和最大值，得出结论．‎ ‎【解答】解：∵，∴函数的周期为T=2π，‎ 函数的最大值为2，且函数取得最大值时，x+=2kπ+，即x=2kπ+，k∈Z．‎ ‎　‎ ‎27．如图，汽车前灯反射镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反射镜的轴垂直，灯泡位于抛物线的焦点F处．已知灯口直径是24cm，灯深10cm，求灯泡与反射镜的顶点O的距离．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】先设出抛物线的标准方程y2=2px（p＞0），点（10，12）代入抛物线方程求得p，进而求得，即灯泡与反光镜的顶点的距离．‎ ‎【解答】解：建立平面直角坐标系，以O为坐标原点，水平方向为x轴，竖直方向为y轴，如图所示：‎ 则：设抛物线方程为y2=2px（p＞0），点（10，12）在抛物线y2=2px上，‎ ‎∴144=2p×10．‎ ‎∴=3.6．‎ ‎∴灯泡与反射镜的顶点O的距离3.6cm．‎ ‎　‎ ‎28．已知数列{an}是公差为2的等差数列．‎ ‎（1）a1，a3，a4成等比数列，求a1的值；‎ ‎（2）设a1=﹣19，数列{an}的前n项和为Sn．数列{bn}满足，记（n∈N*），求数列{cn}的最小项（即对任意n∈N*成立）．‎ ‎【考点】等差数列的前n项和；等比数列的通项公式．‎ ‎【分析】（1）利用等差数列通项公式和等比数列性质能求出首项a1的值．‎ ‎（2）由已知利用累加法能求出bn=2﹣（）n﹣1．从而能求出cn﹣cn﹣1=2n﹣19+2n，由此能求出数列{cn}的最小项．‎ ‎【解答】解：（1）∵数列{an}是公差为2的等差数列．a1，a3，a4成等比数列，‎ ‎∴．‎ 解得d=2，a1=﹣8‎ ‎（2）bn=b1+（b2﹣b1）+（b3﹣b2）+…+（bn﹣bn﹣1）‎ ‎=1+‎ ‎=‎ ‎=2﹣（）n﹣1．‎ ‎，‎ ‎，‎ ‎=2n﹣19+2n 由题意n≥9，上式大于零，即c9＜c10＜…＜cn，‎ 进一步，2n+2n是关于n的增函数，‎ ‎∵2×4+24=24＞19，2×3+23=14＜19，‎ ‎∴c1＞c2＞c3＞c4＜c5＜…＜c9＜c10＜…＜cn，‎ ‎∴．‎ ‎　‎ ‎29．对于函数f（x），g（x），记集合Df＞g={x|f（x）＞g（x）}．‎ ‎（1）设f（x）=2|x|，g（x）=x+3，求Df＞g；‎ ‎（2）设f1（x）=x﹣1，，h（x）=0，如果．求实数a的取值范围．‎ ‎【考点】其他不等式的解法；集合的表示法．‎ ‎【分析】（1）直接根据新定义解不等式即可，‎ ‎（2）方法一：由题意可得则在R上恒成立，分类讨论，即可求出a的取值范围，‎ 方法二：够造函数，求出函数的最值，即可求出a的取值范围．‎ ‎【解答】解：（1）由2|x|＞x+3，得Df＞g={x|x＜﹣1或x＞3}；‎ ‎（2）方法一：，，‎ 由，‎ 则在R上恒成立，‎ 令，a＞﹣t2﹣t，，‎ ‎∴a≥0时成立．‎ 以下只讨论a＜0的情况 对于，‎ ‎=t＞0，t2+t+a＞0，解得t＜或t＞，（a＜0）‎ 又t＞0，所以，‎ ‎∴=‎ 综上所述：‎ 方法二（2），，‎ 由a≥0．显然恒成立，‎ 即x∈Ra＜0时，，在x≤1上恒成立 令，，‎ 所以，‎ 综上所述：．‎ ‎　‎ 二卷一.选择题：‎ ‎30．若函数f（x）=sin（x+φ）是偶函数，则ϕ的一个值是（　　）‎ A．0 B． C．π D．2π ‎【考点】正弦函数的图象．‎ ‎【分析】由函数的奇偶性可得φ的取值范围，结合选项验证可得．‎ ‎【解答】解：∵函数f（x）=sin（x+φ）是偶函数，‎ ‎∴f（﹣x）=f（x），即sin（﹣x+φ）=sin（x+φ），‎ ‎∴（﹣x+φ）=x+φ+2kπ或﹣x+φ+x+φ=π+2kπ，k∈Z，‎ 当（﹣x+φ）=x+φ+2kπ时，可得x=﹣kπ，不满足函数定义；‎ 当﹣x+φ+x+φ=π+2kπ时，φ=kπ+，k∈Z，‎ 结合选项可得B为正确答案．‎ 故选：B．‎ ‎　‎ ‎31．在复平面上，满足|z﹣1|=4的复数z的所对应的轨迹是（　　）‎ A．两个点 B．一条线段 C．两条直线 D．一个圆 ‎【考点】复数的代数表示法及其几何意义．‎ ‎【分析】设z=x+yi，得到|x+yi﹣1|==4，从而求出其运动轨迹．‎ ‎【解答】解：设z=x+yi，‎ 则|x+yi﹣1|==4，‎ ‎∴（x﹣1）2+y2=16，‎ ‎∴运动轨迹是圆，‎ 故选：D．‎ ‎　‎ ‎32．已知函数y=f（x）的图象是折线ABCDE，如图，其中A（1，2），B（2，1），C（3，2），D（4，1），E（5，2），若直线y=kx+b与y=f（x）的图象恰有四个不同的公共点，则k的取值范围是（　　）‎ A．（﹣1，0）∪（0，1） B． C．（0，1] D．‎ ‎【考点】函数的图象．‎ ‎【分析】根据图象使用特殊值验证，使用排除法得出答案．‎ ‎【解答】解；当k=0，1＜b＜2时，显然直线y=b与f（x）图象交于四点，故k可以取0，排除A，C；‎ 作直线BE，则kBE=，直线BE与f（x）图象交于三点，‎ 平行移动直线BD可发现直线与f（x）图象最多交于三点，‎ 即直线y=与f（x）图象最多交于三点，∴k≠．排除D．‎ 故选B．‎ ‎　‎ 二.填空题：‎ ‎33．椭圆的长半轴的长为　5　．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】利用椭圆性质求解．‎ ‎【解答】解：椭圆中，‎ a=5，‎ ‎∴椭圆的长半轴长a=5．‎ 故答案为：5．‎ ‎　‎ ‎34．已知圆锥的母线长为10，母线与轴的夹角为30°，则该圆锥的侧面积为　50π　．‎ ‎【考点】旋转体（圆柱、圆锥、圆台）．‎ ‎【分析】根据勾股定理得出圆锥的底面半径，代入侧面积公式计算．‎ ‎【解答】解：∵圆锥的母线长为10，母线与轴的夹角为30°，‎ ‎∴圆锥的底面半径为5，‎ ‎∴圆锥的侧面积为π×5×10=50π．‎ 故答案为：50π．‎ ‎　‎ ‎35．小明用数列{an}记录某地区2015年12月份31天中每天是否下过雨，方法为：当第k天下过雨时，记ak=1，当第k天没下过雨时，记ak=﹣1（1≤k≤31），他用数列{bn}记录该地区该月每天气象台预报是否有雨，方法为：当预报第k天有雨时，记bn=1，当预报第k天没有雨时，记bn=﹣1记录完毕后，小明计算出a1b1+a2b2+a3b3+…+a31b31=25，那么该月气象台预报准确的总天数为　28　．‎ ‎【考点】数列的应用．‎ ‎【分析】由题意，气象台预报准确时akbk=1，不准确时akbk=﹣1，根据a1b1+a2b2+a3b3+…+a31b31=25=28﹣3，即可得出结论．‎ ‎【解答】解：由题意，气象台预报准确时akbk=1，不准确时akbk=﹣1，‎ ‎∵a1b1+a2b2+a3b3+…+a31b31=25=28﹣3，‎ ‎∴该月气象台预报准确的总天数为28．‎ 故答案为：28．‎ ‎　‎ 三.解答题：‎ ‎36．对于数列{an}与{bn}，若对数列{cn}的每一项cn，均有ck=ak或ck=bk，则称数列{cn}是{an}与{bn}的一个“并数列”．‎ ‎（1）设数列{an}与{bn}的前三项分别为a1=1，a2=3，a3=5，b1=1，b2=2，b3=3，若{cn}是{an}与{bn}一个“并数列”求所有可能的有序数组（c1，c2，c3）；‎ ‎（2）已知数列{an}，{cn}均为等差数列，{an}的公差为1，首项为正整数t；{cn}的前10项和为﹣30，前20项的和为﹣260，若存在唯一的数列{bn}，使得{cn}是{an}与{bn}的一个“并数列”，求t的值所构成的集合．‎ ‎【考点】数列的求和；数列的应用．‎ ‎【分析】（1）利用“并数列”的定义即可得出．‎ ‎（2）利用等差数列的通项公式及其前n项和公式可得an，公差d，cn，通过分类讨论即可得出．‎ ‎【解答】解：（1）（1，2，3），（1，2，5），（1，3，3），（1，3，5）；‎ ‎（2）an=t+n﹣1，‎ 设{cn}的前10项和为Tn，T10=﹣30，T20=﹣260，得d=﹣2，c1=6，所以cn=8﹣2n；ck=ak或ck=bk．，‎ ‎∴k=1，t=6；或k=2，t=3，‎ 所以k≥3．k∈N*时，ck=bk，‎ ‎∵数列{bn}唯一，所以只要b1，b2唯一确定即可．‎ 显然，t=6，或t=3时，b1，b2不唯一，‎ ‎．‎ ‎　‎ ‎2016年7月25日