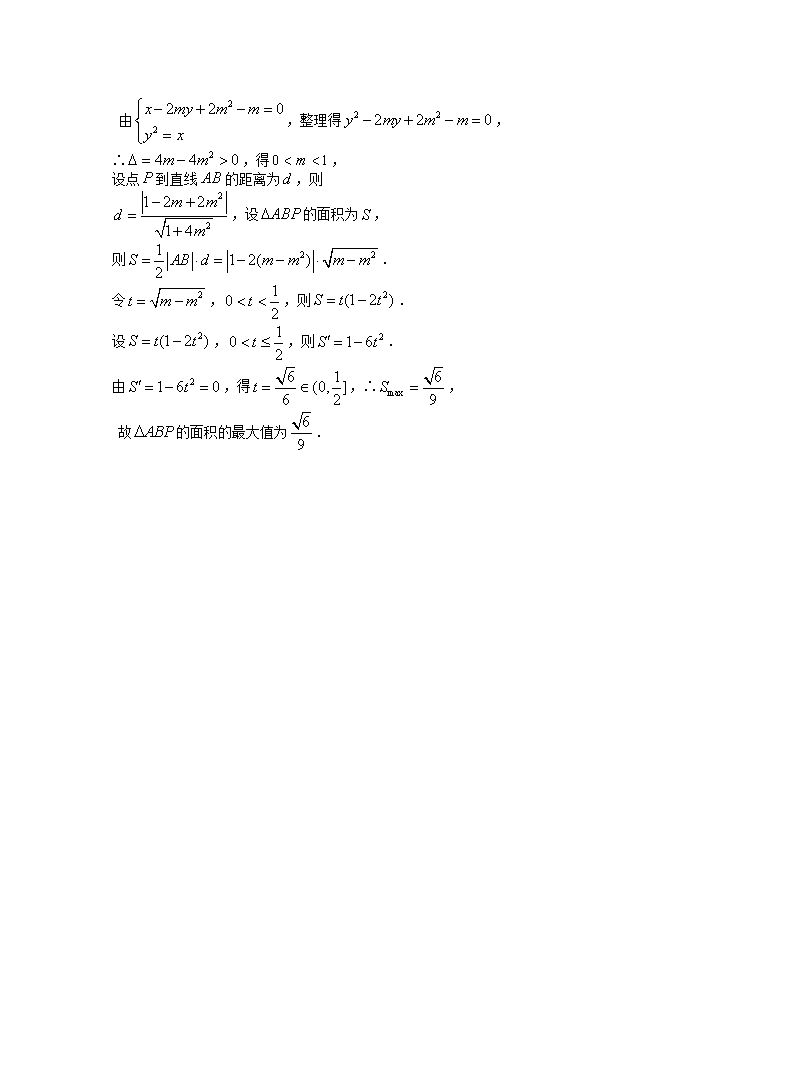三维设计广东文人教版2014高考数学第一轮复习考案 抛物线 文 3页

第67课 抛物线 ‎ ‎1．（2019四川高考）已知抛物线关于轴对称，它的顶点在坐标原点，并且经过点．若点到该抛物线焦点的距离为，则（ ）‎ A． B． C． D．‎ ‎【答案】B ‎ 【解析】可设抛物线方程为，‎ ‎∵点到该抛物线焦点的距离为，‎ ‎∵点在抛物线上，∴，‎ ‎2．（2019安徽高考）过抛物线的焦点的直线交抛物线于两点，点是原点，若，则的面积为（ ）‎ ‎【答案】C ‎【解析】∵，∴，∴，，取，‎ ‎3．（2019新课标高考）等轴双曲线的中心在原点，焦点在轴上，与抛物线的准线交于两点，，则双曲线的实轴长为（ ）‎ ‎ A． B． C． D．‎ ‎【答案】C ‎【解析】由题设知抛物线的准线为：，‎ 设等轴双曲线方程为：，‎ 将代入双曲线方程得，‎ 解得，∴实轴长，选C．‎ ‎4．（2019福建高考）已知双曲线的右焦点与抛物线的焦点重合，则该双曲线的焦点到其渐近线的距离等于（ ）‎ A． B． C． D．‎ ‎【答案】Ａ．‎ ‎ 【解析】∵抛物线的焦点坐标为，∴，∴，‎ ‎∴双曲线的渐进线方程为，即，‎ ‎∴，故选Ａ．‎ ‎5．（2019深圳二模）已知抛物线：的焦点为，过点作直线交抛物线于、两点；椭圆的中心在原点，焦点在轴上，点是它的一个顶点，且其离心率．‎ ‎（1）求椭圆的方程；‎ ‎（2）经过、两点分别作抛物线的切线、，切线与相交于点．‎ 证明：．‎ ‎【解析】（1）设椭圆的方程为，半焦距为．‎ M B A F O 由已知条件，得，‎ ‎∴，解得． .‎ ‎∴椭圆的方程为：． ‎ ‎（2）显然直线的斜率存在，‎ 否则直线与抛物线只有一个交点，不合题意，‎ ‎ 故可设直线的方程为，‎ ‎ 由，得， ‎ ‎∵抛物线的方程为，求导得，‎ ‎∴过抛物线上、两点的切线方程分别是 即 ，，‎ 解得两条切线、的交点的坐标为 ‎，即．‎ ‎6．（2019浙江高考）如图，在直角坐标系中，点到抛物线：（）的准线的距离为．点是上的定点，是上的两动点，且线段被直线平分．‎ ‎（1）求，的值．‎ ‎（2）求面积的最大值．‎ ‎【解析】（1）由题意得，得．‎ ‎（2）由（1）可知直线的方程为，设，‎ ‎∵线段被直线平分．‎ ‎∴可设线段的中点坐标为 由题意得，设直线的斜率为．‎ 由（1）可知抛物线方程为 由，得，‎ ‎∴，得，‎ ‎∴直线的方程为，即．‎ 由，整理得，‎ ‎∴，得，‎ 设点到直线的距离为，则 ‎，设的面积为，‎ 则．‎ 令，，则．‎ 设，，则．‎ 由，得，∴，‎ 故的面积的最大值为．‎