- 80.00 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
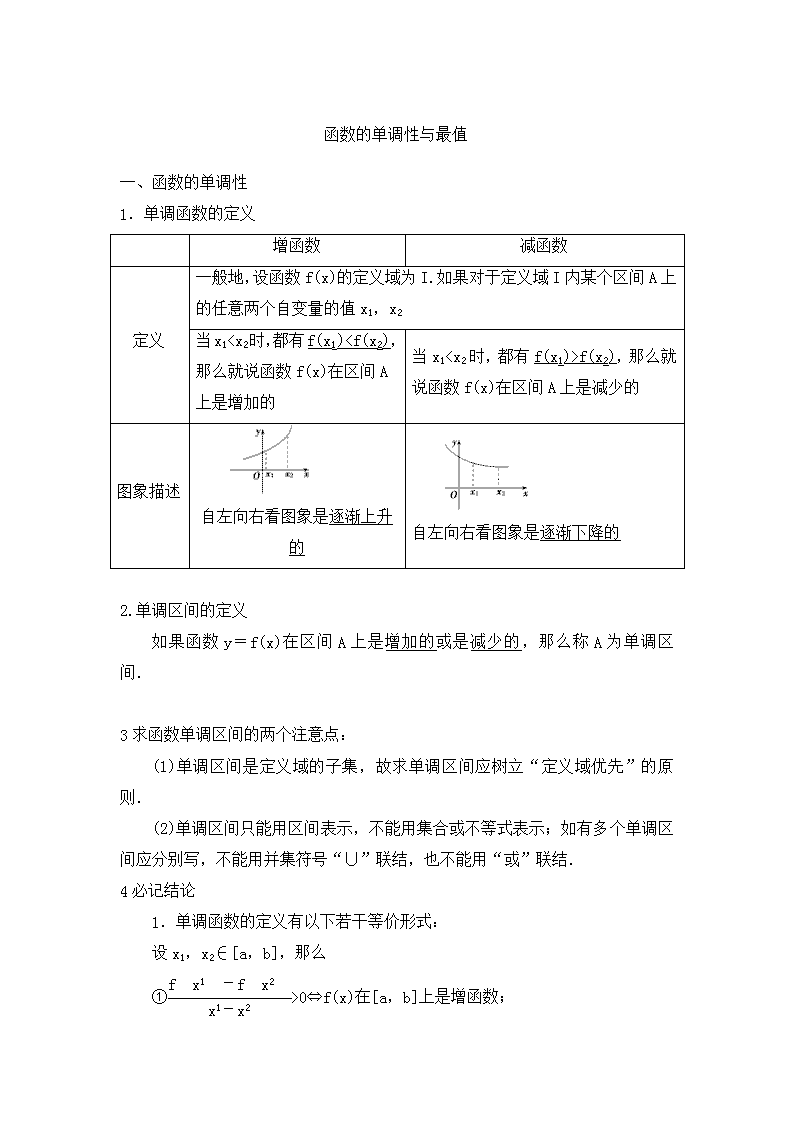
函数的单调性与最值
一、函数的单调性
1.单调函数的定义
增函数
减函数
定义
一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间A上的任意两个自变量的值x1,x2
当x1f(x2),那么就说函数f(x)在区间A上是减少的
图象描述
自左向右看图象是逐渐上升的
自左向右看图象是逐渐下降的
2.单调区间的定义
如果函数y=f(x)在区间A上是增加的或是减少的,那么称A为单调区间.
3求函数单调区间的两个注意点:
(1)单调区间是定义域的子集,故求单调区间应树立“定义域优先”的原则.
(2)单调区间只能用区间表示,不能用集合或不等式表示;如有多个单调区间应分别写,不能用并集符号“∪”联结,也不能用“或”联结.
4必记结论
1.单调函数的定义有以下若干等价形式:
设x1,x2∈[a,b],那么
①>0⇔f(x)在[a,b]上是增函数;
<0⇔f(x)在[a,b]上是减函数.
②(x1-x2)[f(x1)-f(x2)]>0⇔f(x)在[a,b]上是增函数;
(x1-x2)[f(x1)-f(x2)]<0⇔f(x)在[a,b]上是减函数.
2.复合函数y=f[g(x)]的单调性规律是“同则增,异则减”,即y=f(u)与u=g(x)若具有相同的单调性,则y=f[g(x)]为增函数,若具有不同的单调性,则y=f[g(x)]必为减函数.
考点一 函数单调性的判断
1.下列四个函数中,在(0,+∞)上为增函数的是( )
A.f(x)=3-x B.f(x)=x2-3x
C.f(x)=- D.f(x)=-|x|
解析:当x>0时,f(x)=3-x为减函数;
当x∈时,f(x)=x2-3x为减函数,
当x∈时,f(x)=x2-3x为增函数;
当x∈(0,+∞)时,f(x)=-为增函数;
当x∈(0,+∞)时,f(x)=-|x|为减函数.故选C.答案:C
2.判断函数g(x)=在(1,+∞)上的单调性.
解:法一:定义法
任取x1,x2∈(1,+∞),且x10,
因此g(x1)-g(x2)<0,即g(x1)0,
∴g(x)在(1,+∞)上是增函数.
给出解析式函数单调性的两种判定方法
1.定义法(基本步骤为取值、作差或作商、变形、判断).
*2.导数法(基本步骤为求定义域、求导、变形、判断).
考点二 函数的单调区间的求法|
1求下列函数的单调区间:
(1)y=-x2+2|x|+1;
(2)y=log(x2-3x+2).
[解] (1)由于
y=
即y=
画出函数图象如图所示,
单调递增区间为(-∞,-1]和[0,1],
单调递减区间为[-1,0]和[1,+∞).
(2)令u=x2-3x+2,则原函数可以看作y=logu与u=x2-3x+2的复合函数.
令u=x2-3x+2>0,则x<1或x>2.
∴函数y=log(x2-3x+2)的定义域为(-∞,1)∪(2,+∞).
又u=x2-3x+2的对称轴x=,且开口向上.
∴u=x2-3x+2在(-∞,1)上是单调减函数,在(2,+∞)上是单调增函数.
而y=logu在(0,+∞)上是单调减函数,
∴y=log(x2-3x+2)的单调递减区间为(2,+∞),单调递增区间为(-∞,1).
函数单调区间的四种求法
(1)利用已知函数的单调性,即转化为已知函数的和、差或复合函数,求单调区间.
(2)定义法:先求定义域,再利用单调性定义.
(3)图象法:如果f(x)是以图象形式给出的,或者f(x)的图象易作出,可由图象的直观性写出它的单调区间.
*(4)导数法:利用导数取值的正负确定函数的单调区间.
2函数y=|x|(1-x)在区间A上是增函数,那么区间A是( )
A.(-∞,0) B.
C.[0,+∞) D.
解析:y=|x|(1-x)
==
=
画出函数的草图,如图.
由图易知原函数在上单调递增.
答案:B
考点三 函数单调性的应用
函数单调性的应用比较广泛,是每年高考的重点和热点内容.归纳起来,常见的命题探究角度有:
1.求函数的值域或最值.
2.比较两个函数值或两个自变量的大小.
3.解函数不等式.
4.求参数的取值范围或值.
一 求函数的值域或最值
1.已知函数f(x)=则f(f(-3))=________,f(x)的最小值是________.
二 比较两个函数值或两自变量的大小
2.已知函数f(x)=log2x+,若x1∈(1,2),x2∈(2,+∞),则( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
三 解函数不等式
3.已知函数f(x)=若f(2-x2)>f(x),则实数x的取值范围是( )
A.(-∞,-1)∪(2,+∞)
B.(-∞,-2)∪(1,+∞)
C.(-1,2)
D.(-2,1)
四 利用单调性求参数的取值范围
4.已知f(x)=满足对任意x1≠x2,都有>0成立,那么a的取值范围是( )
A. B.
C.(1,2) D.(1,+∞)
1.解析:由题知,f(-3)=1,f(1)=0,即f(f(-3))=0.又f(x)在(-∞,0)上单调递减,在(0,1)上单调递增,在(1,)上单调递减,在(,+∞)上单调递增,所以f(x)min=min{f(0),f()}=2-3.
答案:0 2-3
2.解析:∵函数f(x)=log2x+在(1,+∞)上为增函数,且f(2)=0,
∴当x1∈(1,2)时,f(x1)f(2)=0,
即f(x1)<0,f(x2)>0.
答案:B
3.解析:∵当x=0时,两个表达式对应的函数值都为零,∴函数的图象是一条连续的曲线.∵当x≤0时,函数f(x)=x3为增函数,当x>0时,f(x)=ln(x+1)也是增函数,且当x1<0,x2>0时,f(x1)f(x)等价于2-x2>x,即x2+x-2<0,解得-20时,有f(x)>1.
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,解不等式f(2t-1)-f(1+t)<2.
[规范解答] (1)证明:设x1,x2∈R且x10,
∴f(x2-x1)>1.(2分)
根据条件等式有
f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x2-x1)+f(x1)-1-f(x1)=f(x2
-x1)-1>0,
∴f(x1)f(3a)的解集为( )
A.(2,6) B.(-1,4)
C.(1,4) D.(-3,5)
5.如果函数y=f(x)在区间I上是增函数,且函数y=在区间I上是减函数,那么称函数y=f(x)是区间I上的“缓增函数”,区间I叫作“缓增区间”.若函数f(x)=x2-x+是区间I上的“缓增函数”,则“缓增区间”I为( )
A.[1,+∞) B.[0,]
C.[0,1] D.[1,]
6.已知f(x)是定义在R上的偶函数,若对任意的x1,x2∈[0,+∞)(x1≠x2),有<0,则f(3),f(-2),f(1)的大小关系为________.
7.设函数f(x)=g(x)=x2f(x-1),则函数g(x)的递减区间是________.
8.已知函数f(x)=|x+a|在(-∞,-1)上是单调函数,则a的取值范围是________.
9.已知f(x)=(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)上单调递增;
(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.
10.已知函数g(x)=+1,h(x)=,x∈(-3,a],其中a为常数且a>0,令函数f(x)=g(x)·h(x).
(1)求函数f(x)的表达式,并求其定义域;
(2)当a=时,求函数f(x)的值域.
练习B组
1.下列函数中,在区间(0,+∞)上为增函数的是( )
A.y= B.y=(x-1)2
C.y=2-x D.y=log0.5(x+1)
*2. “a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
3.若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________.
4. a为实数,函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a).当a=________时,g(a)的值最小.
答案
1.解析:因为定义域是R,排除C,又是增函数,排除A、D,所以选B.
答案:B
2.解析:依题意,注意到y=3-x与函数y=的值域均是R,函数y=的值域是(0,1],函数y=x2+2x-10=(x+1)2-11的值域是[-11,+∞),因此选B.
答案:B
3.解析:注意到f(x)=-(x-a)2+a2;依题意得即0f(3a),可得a2-4<3a,整理得a2-3a-4<0,即(a+1)(a-4)<0,解得-1f(-2)>f(3).
即f(1)>f(2)>f(3).
答案:f(1)>f(-2)>f(3)
7.解析:g(x)=如图所示,其递减区间是[0,1).
答案:[0,1)
8.解析:因为函数f(x)在(-∞,-a)上是单调函数,所以-a≥-1,解得a≤1.
答案:(-∞,1]
9.解:(1)证明:任设x10,x1-x2<0,
∴f(x1)0时,f(x)在(-∞,a),(a,+∞)上是减函数,
又f(x)在(1,+∞)上单调递减,
∴00).
(2)函数f(x)的定义域为,
令+1=t,则x=(t-1)2,t∈,
f(x)=F(t)==.
∵t=时,t=±2∉,又t∈时,t+单调递减,F(t)单调递增,
∴F(t)∈.
即函数f(x)的值域为.
1.解析:y=(x-1)2仅在[1,+∞)上为增函数,排除B;y=2-x=x为减函数,排除C;因为y=log0.5t为减函数,t=x+1为增函数,所以y=log0.5(x+1)为减函数,排除D;y=和t=x+1均为增函数,所以y=为增函数,故选A.
答案:A
2.解析:由二次函数的图象和性质知f(x)=|(ax-1)x|在(0,+∞)内单调递增,只需f(x)的图象在(0,+∞)上与x轴无交点,即a=0或<0,整理得a≤0,而当a≤0时,结合图象(图略)可知f(x)在(0,+∞)上为增函数.故a≤0是f(x)在(0,+∞)上单调递增的充要条件,故选C.
答案:C
3.解析:因为f(x)=所以当x≤2时,f(x)≥4;又函数f(x)的值域为[4,+∞),所以解得10,即x>-,而y=log5u为(0,+∞)上的增函数,当x>-时,u=2x+1也为R上的增函数,故原函数的单调增区间是.答案:
3.解析:要使函数在R上是增函数,
则有
解得-3≤a≤-2,即a的取值范围是[-3,-2].答案:B
相关文档
- (浙江专用)备战2020高考物理一轮复习2021-05-1315页
- 高考作文热点之五中华文化传统2021-05-1334页
- 2020高考物理一轮复习 专题 两类匀2021-05-132页
- (浙江专用)2020高考语文二轮复习 精2021-05-134页
- 2020版高考地理一轮总复习 第二单2021-05-136页
- (浙江选考)2020版高考英语大二轮复习2021-05-135页
- 高考地理常见天气系统一轮过关测试2021-05-138页
- 2020版高考英语阅读理解一轮提升选2021-05-1311页
- 2020高考地理 选考 区域地理 第二2021-05-135页
- 2020版高考历史二轮专题复习专题92021-05-1324页