浙江省杭州市学军中学高考数学模拟试卷月份 28页

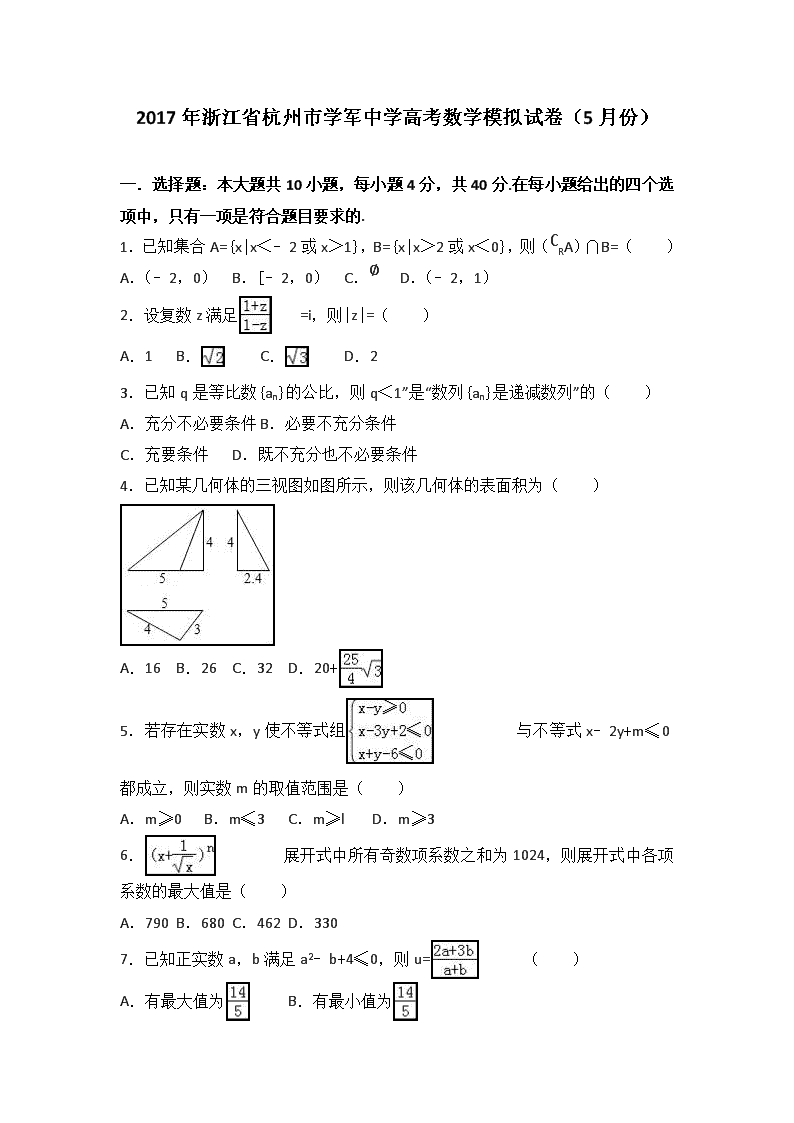
‎2017年浙江省杭州市学军中学高考数学模拟试卷（5月份）‎ ‎　‎ 一．选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知集合A={x|x＜﹣2或x＞1}，B={x|x＞2或x＜0}，则（∁RA）∩B=（　　）‎ A．（﹣2，0） B．[﹣2，0） C．∅ D．（﹣2，1）‎ ‎2．设复数z满足=i，则|z|=（　　）‎ A．1 B． C． D．2‎ ‎3．已知q是等比数{an}的公比，则q＜1”是“数列{an}是递减数列”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．已知某几何体的三视图如图所示，则该几何体的表面积为（　　） ‎ A．16 B．26 C．32 D．20+‎ ‎5．若存在实数x，y使不等式组与不等式x﹣2y+m≤0都成立，则实数m的取值范围是（　　）‎ A．m≥0 B．m≤3 C．m≥l D．m≥3‎ ‎6．展开式中所有奇数项系数之和为1024，则展开式中各项系数的最大值是（　　）‎ A．790 B．680 C．462 D．330‎ ‎7．已知正实数a，b满足a2﹣b+4≤0，则u=（　　）‎ A．有最大值为 B．有最小值为 C．没有最小值 D．有最大值为3‎ ‎8．已知正三角形ABC的边长为2，平面ABC内的动点P，M满足||=1， =，则||2的最大值是（　　）‎ A． B． C． D．‎ ‎9．如图，正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是，PQ是正方形BDEF所在平面内的一条动直线，则直线BD与PQ所成角的取值范围是（　　）‎ A．[，] B．[，] C．[，] D．[，]‎ ‎10．已知定义在（0，+∞）上的函数f（x）的导函数f'（x）满足，且，其中e为自然对数的底数，则不等式的解集是（　　）‎ A． B．（0，e） C． D．‎ ‎　‎ 二．填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.‎ ‎11．若2sinα﹣cosα=，则sinα=　 　，tan（α﹣）=　 　．‎ ‎12．商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖．每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球．在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖．则顾客抽奖1次能获奖的概率是　 　；若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为X，则EX=　 　．‎ ‎13．在△ABC中，D是AC边的中点，A=，cos∠BDC=﹣，△ABC的面积为3，则sin∠ABD=　 　，BC=　 　．‎ ‎14．已知抛物线y=x2和直线l：y=kx+m（m＞0）交于两点A、B，当时，直线l过定点　 　；当m=　 　时，以AB为直径的圆与直线相切．‎ ‎15．根据浙江省新高考方案，每位考生除语、数、外3门必考科目外，有3门选考科目，并且每门选考科目都有2次考试机会，每年有两次考试时间，某考生为了取得最好成绩，将3门选考科目共6次考试机会安排在高二与高三的4次考试中，且每次至多考2门，则该考生共有　 　 种不同的考试安排方法．‎ ‎16．如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，P，Q，R分别是棱AB，AD，AA1的中点．以△PQR为底面作一个直三棱柱，使其另一个底面的三个顶点也都在此正方体的表面上．则这个直三棱柱的体积是　 　．‎ ‎17．函数y=ax2﹣2x的图象上有且仅有两个点到直线y=x的距离等于，则实数a的取值集合是　 　．‎ ‎　‎ 三．解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.‎ ‎18．设函数f（x）=sin2ωx﹣cos2ωx+2sinωxcosωx+λ的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（，1）．‎ ‎（Ⅰ）求函数f（x）的最小正周期；‎ ‎（Ⅱ）若y=f（x）的图象经过点（，0），求函数f（x）在区间[0，]上的取值范围．‎ ‎19．在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O′的直径，FB是圆台的一条母线．‎ ‎（I）已知G，H分别为EC，FB的中点，求证：GH∥平面ABC；‎ ‎（Ⅱ）已知EF=FB=AC=2，AB=BC，求二面角F﹣BC﹣A的余弦值．‎ ‎20．已知函数f（x）=+x（a，b∈R）．‎ ‎（Ⅰ）当a=2，b=3时，求函数f（x）极值；‎ ‎（Ⅱ）设b=a+1，当0≤a≤1时，对任意x∈[0，2]，都有m≥|f'（x）|恒成立，求m的最小值．‎ ‎21．已知椭圆+y2=1（a＞1），过直线l：x=2上一点P作椭圆的切线，切点为A，当P点在x轴上时，切线PA的斜率为±．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设O为坐标原点，求△POA面积的最小值．‎ ‎22．已知函数fn（x）=xn（1﹣x）2在（，1）上的最大值为an ‎（n=1，2，3，…）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）求证：对任何正整数n（n≥2），都有an≤成立；‎ ‎（3）设数列{an}的前n项和为Sn，求证：对任意正整数n，都有Sn＜成立．‎ ‎　‎ ‎2017年浙江省杭州市学军中学高考数学模拟试卷（5月份）‎ 参考答案与试题解析 ‎　‎ 一．选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．已知集合A={x|x＜﹣2或x＞1}，B={x|x＞2或x＜0}，则（∁RA）∩B=（　　）‎ A．（﹣2，0） B．[﹣2，0） C．∅ D．（﹣2，1）‎ ‎【考点】1H：交、并、补集的混合运算．‎ ‎【分析】由全集R及A，求出A的补集，找出B与A补集的交集即可．‎ ‎【解答】解：∵集合A={x|x＜﹣2或x＞1}，‎ ‎∴∁RA={x|﹣2≤x≤1}，‎ 集合BB={x|x＞2或x＜0}，‎ ‎∴（∁RA）∩B={x|﹣2≤x＜0}=[﹣2，0），‎ 故选：B．‎ ‎　‎ ‎2．设复数z满足=i，则|z|=（　　）‎ A．1 B． C． D．2‎ ‎【考点】A8：复数求模．‎ ‎【分析】先化简复数，再求模即可．‎ ‎【解答】解：∵复数z满足=i，‎ ‎∴1+z=i﹣zi，‎ ‎∴z（1+i）=i﹣1，‎ ‎∴z==i，‎ ‎∴|z|=1，‎ 故选：A．‎ ‎　‎ ‎3．已知q是等比数{an}的公比，则q＜1”是“数列{an}是递减数列”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【考点】2L：必要条件、充分条件与充要条件的判断．‎ ‎【分析】题目给出的数列是等比数列，通过举反例说明公比小于1时数列还可能是递增数列，反之，递减的等比数列公比还可能大于1，从而得到“q＜1”是“等比数列{an}是递减数列”的既不充分也不必要的条件．‎ ‎【解答】解：数列﹣8，﹣4，﹣2，…，该数列是公比q=的等比数列，但该数列是递增数列，所以，由等比数{an}的公比q＜1，不能得出数列{an}是递减数列；‎ 而数列﹣1，﹣2，﹣4，﹣8，…是递减数列，但其公比q=，所以，由数列{an}是递减数列，不能得出其公比 q＜1．‎ 所以，“q＜1”是“等比数列{an}是递减数列”的既不充分也不必要的条件．‎ 故选D．‎ ‎　‎ ‎4．已知某几何体的三视图如图所示，则该几何体的表面积为（　　） ‎ A．16 B．26 C．32 D．20+‎ ‎【考点】L!：由三视图求面积、体积．‎ ‎【分析】几何体是三棱锥，根据三视图可得三棱锥的一侧棱与底面垂直，结合直观图求相关几何量的数据，把数据代入棱锥的表面积公式计算即可．‎ ‎【解答】解：根据三视图知：该几何体是三棱锥，且三棱锥的一个侧棱与底面垂直，高为4，‎ 如图所示：‎ 其中SC⊥平面ABC，SC=3，AB=4，BC=3，AC=5，SC=4，∴AB⊥BC，‎ 由三垂线定理得：AB⊥BC，‎ S△ABC=×3×4=6，‎ S△SBC=×3×4=6，‎ S△SAC=×4×5=10，‎ S△SAB=×AB×SB=×4×5=10，‎ ‎∴该几何体的表面积S=6+6+10+10=32．‎ 故选：C．‎ ‎　‎ ‎5．若存在实数x，y使不等式组与不等式x﹣2y+m≤0都成立，则实数m的取值范围是（　　）‎ A．m≥0 B．m≤3 C．m≥l D．m≥3‎ ‎【考点】7C：简单线性规划．‎ ‎【分析】作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=x﹣2y对应的直线进行平移，可得当x=y=3时，z取得最小值为﹣3；当x=4且y=2时，z取得最大值为0，由此可得z的取值范围为[﹣3，0]，再由存在实数m使不等式x﹣2y+m≤0成立，即可算出实数m的取值范围．‎ ‎【解答】解：作出不等式组表示的平面区域，‎ 得到如图的△ABC及其内部，其中A（4，2），B（1，1），C（3，3）‎ 设z=F（x，y）=x﹣2y，将直线l：z=x﹣2y进行平移，‎ 当l经过点A时，目标函数z达到最大值，可得z最大值=F（4，2）=0‎ 当l经过点C时，目标函数z达到最小值，可得z最小值=F（3，3）=﹣3‎ 因此，z=x﹣2y的取值范围为[﹣3，0]，‎ ‎∵存在实数m，使不等式x﹣2y+m≤0成立，即存在实数m，使x﹣2y≤﹣m成立 ‎∴﹣m大于或等于z=x﹣2y的最小值，即﹣3≤﹣m，解之得m≤3‎ 故选：B ‎　‎ ‎6．展开式中所有奇数项系数之和为1024，则展开式中各项系数的最大值是（　　）‎ A．790 B．680 C．462 D．330‎ ‎【考点】DB：二项式系数的性质．‎ ‎【分析】由题意可得：2n﹣1=1024，解得n=11．可得展开式中各项系数的最大值是或．‎ ‎【解答】解：由题意可得：2n﹣1=1024，解得n=11．‎ 则展开式中各项系数的最大值是或，则==462．‎ 故选：C．‎ ‎　‎ ‎7．已知正实数a，b满足a2﹣b+4≤0，则u=（　　）‎ A．有最大值为 B．有最小值为 C．没有最小值 D．有最大值为3‎ ‎【考点】7F：基本不等式．‎ ‎【分析】a2﹣b+4≤0，可得b≥a2+4，a，b＞0．可得﹣≥﹣，再利用基本不等式的性质即可得出．‎ ‎【解答】解：∵a2﹣b+4≤0，∴b≥a2+4，a，b＞0．‎ ‎∴a+b≥a2+a+4，‎ ‎∴≤，‎ ‎∴﹣≥﹣，‎ ‎∴u==3﹣≥3﹣=3﹣≥3﹣=，当且仅当a=2，b=8时取等号．‎ 故选：B．‎ ‎　‎ ‎8．已知正三角形ABC的边长为2，平面ABC内的动点P，M满足||=1， =，则||2的最大值是（　　）‎ A． B． C． D．‎ ‎【考点】93：向量的模．‎ ‎【分析】如图所示，建立直角坐标系．B（0，0），C．A．点P的轨迹方程为： =1，令x=+cosθ，y=3+sinθ，θ∈[0，2π）．又=，可得M ‎，代入||2=+3sin，即可得出．‎ ‎【解答】解：如图所示，建立直角坐标系．‎ B（0，0），C．‎ A．‎ ‎∵M满足||=1，‎ ‎∴点P的轨迹方程为： =1，‎ 令x=+cosθ，y=3+sinθ，θ∈[0，2π）．‎ 又=，则M，‎ ‎∴||2=+=+3sin≤．‎ ‎∴||2的最大值是．‎ 也可以以点A为坐标原点建立坐标系．‎ 故选：B．‎ ‎　‎ ‎9．如图，正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是，PQ是正方形BDEF所在平面内的一条动直线，则直线BD与PQ所成角的取值范围是（　　）‎ A．[，] B．[，] C．[，] D．[，]‎ ‎【考点】LM：异面直线及其所成的角．‎ ‎【分析】以B为原点，BC为x轴，BA为y轴，过B作平面ABCD的垂线为z轴，建立空间直角坐标系，利用向量法能求出直线BD与PQ所成角的取值范围．‎ ‎【解答】解：以B为原点，BC为x轴，BA为y轴，过B作平面ABCD的垂线为z轴，建立空间直角坐标系，‎ 设BC=1，则B（0，0，0），D（1，1，0），C（1，0，0），‎ E（1，），F（0，，），‎ 当D点在正方形BCEF的投影刚好落在CE上，记为G点，其坐标为G（1，，），‎ 此时BG与BD所成角刚好30度，‎ 即直线BD与PQ所成角的最小值为，‎ 取P（，0，0），Q（0，）时，直线BD于PQ所成角取最大值，‎ ‎∵=（1，1，0），=（﹣，，），‎ ‎∴cos＜＞==0，‎ ‎∴直线BD于PQ所成角最大值为．‎ ‎∴直线BD与PQ所成角的取值范围是[，]．‎ 故选：B．‎ ‎　‎ ‎10．已知定义在（0，+∞）上的函数f（x）的导函数f'（x）满足，且，其中e为自然对数的底数，则不等式的解集是（　　）‎ A． B．（0，e） C． D．‎ ‎【考点】6B：利用导数研究函数的单调性；63：导数的运算；67：定积分．‎ ‎【分析】根据题意，令g（x）=xf（x），分析可得g′（x）=[xf（x）]′=，对g（x）求积分可得g（x）的解析式，进而可得f（x）的解析式，再令h（x）=f（x）﹣x，对其求导可得h′（x）=f′（x）﹣1＜0，分析可得函数h（x）=f（x）﹣x在（0，+∞）上递减，将不等式变形可得f（x）﹣x＞﹣e=f（e）﹣e，结合函数的单调性分析可得答案．‎ ‎【解答】解：根据题意，令g（x）=xf（x），‎ 则有g′（x）=[xf（x）]′=，‎ 则g（x）=（lnx）2+C，即xf（x）=（lnx）2+C，‎ 则有f（x）=（lnx）2+，‎ 又由，即f（e）=+=，解可得C=，‎ 故f（x）=（lnx）2+，‎ 令h（x）=f（x）﹣x，‎ 则h′（x）=f′（x）﹣1=＜0，‎ 故函数h（x）=f（x）﹣x在（0，+∞）上递减，‎ 不等式，即f（x）﹣x＞﹣e=f（e）﹣e，‎ 则有0＜x＜e，‎ 即不等式的解集为（0，e）；‎ 故选：B．‎ ‎　‎ 二．填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.‎ ‎11．若2sinα﹣cosα=，则sinα=　　，tan（α﹣）=　3　．‎ ‎【考点】GR：两角和与差的正切函数；GH：同角三角函数基本关系的运用．‎ ‎【分析】根据已知及同角三角函数的基本关系式，建立方程关系即可得到结论．‎ ‎【解答】解：∵2sinα﹣cosα=，‎ ‎∴cosα=2sinα﹣，‎ ‎∵sin2α+cos2α=1，‎ ‎∴sin2α+（2sinα﹣）2=1，‎ 即5sin2α﹣4sinα+4=0，‎ ‎∴解得：sinα=，‎ ‎∴cosα=2×﹣=﹣，tan=﹣2，‎ ‎∴tan（α﹣）===3．‎ 故答案为：，3．‎ ‎　‎ ‎12．商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖．每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球．在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖．则顾客抽奖1次能获奖的概率是　　；若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为X，则EX=　　．‎ ‎【考点】CH：离散型随机变量的期望与方差．‎ ‎【分析】利用相互独立事件的概率乘法公式计算不获奖的概率得出获奖的概率，根据二项分布的性质得出数学期望．‎ ‎【解答】解：抽奖1次，不中奖的概率为=，‎ ‎∴抽奖1次能获奖的概率为1﹣=；‎ 抽奖1次获一等奖的概率为=，‎ ‎∴随机变量X服从二项分布，即X～B（3，），‎ ‎∴EX=3×=．‎ 故答案为：，．‎ ‎　‎ ‎13．在△ABC中，D是AC边的中点，A=，cos∠BDC=﹣，△ABC的面积为3，则sin∠ABD=　　，BC=　6　．‎ ‎【考点】HT：三角形中的几何计算．‎ ‎【分析】过B作BH⊥AC于H，则cos∠BDH==，设DH=2k（k＞0），则BD=k，BH=k，在Rt△ABH中，由∠A=，得AH=k，从而AD=3k，AC=6k，由S△ABC==3=3，求出BC=6，再由，能求出sin∠ABD．‎ ‎【解答】解：过B作BH⊥AC于H，则cos∠BDH==，‎ 设DH=2k（k＞0），则BD=k，‎ ‎∴BH==k，‎ 在Rt△ABH中，∠A=，∴AH==k，‎ ‎∴AD=3k，AC=6k，‎ 又S△ABC=×AC×BH==3=3，‎ 解得k=1，∴BC=6，‎ 在△ABD中，，‎ ‎∴‎ 解得sin∠ABD=．‎ 故答案为：，6．‎ ‎　‎ ‎14．已知抛物线y=x2和直线l：y=kx+m（m＞0）交于两点A、B，当时，直线l过定点　（0，2）　；当m=　　时，以AB为直径的圆与直线相切．‎ ‎【考点】K8：抛物线的简单性质．‎ ‎【分析】将直线代入抛物线方程，利用韦达定理及向量数量积的坐标运算，即可求得m的值，求得直线l的方程求得直线l过点（0，2）；‎ 利用中点坐标公式求得圆M的圆心，求得切点坐标，根据向量的数量积的坐标运算，即可求得m的值．‎ ‎【解答】解：设A（x1，y1），B（x2，y2），‎ ‎，整理得：x2﹣kx﹣m=0，‎ 则x1+x2=k，x1x2=﹣m，‎ y1y2=（x1x2）2=m2，y1+y2=k（x1+x2）+2m=k2+2m，‎ 由，则x1x2+y1y2=m2﹣m=2，即m2﹣m﹣2=0，解得：m=﹣1或m=2，‎ 由m＞0，则m=2，‎ 直线l：y=kx+2，‎ ‎∴直线l过点（0，2），‎ 设以AB为直径的圆的圆心M（x，y），圆M与相切于P，‎ 由x==，则P（，﹣），‎ 由题意可知： •=0，即（x1﹣，y1+）•（x2﹣，y2+）=0，‎ 整理得：x1x2﹣（x1+x2）++y1y2+（y1+y2）+=0，‎ 代入整理得：m2﹣+=0，解得：m=，‎ ‎∴当m=，以AB为直径的圆与直线相切．‎ 故答案为：（0，2），．‎ ‎　‎ ‎15．根据浙江省新高考方案，每位考生除语、数、外3门必考科目外，有3门选考科目，并且每门选考科目都有2次考试机会，每年有两次考试时间，某考生为了取得最好成绩，将3门选考科目共6次考试机会安排在高二与高三的4次考试中，且每次至多考2门，则该考生共有　114　 种不同的考试安排方法．‎ ‎【考点】D8：排列、组合的实际应用．‎ ‎【分析】依题意，分两大类：①四次考试中选三次（有种方法），每次考两科；②四次考试都选，有两次考两科，另外两次各考一科，分别分析、计算即可求得答案．‎ ‎【解答】解：将3门选考科目共6次考试机会安排在高二与高三的4次考试中，且每次至多考2门，有两种情况：‎ ‎①四次考试中选三次（有种方法），每次考两科，第一次有种方法，第二次必须考剩下的一科与考过的两科中的一科，有•种方法，第三次只能是种方法，根据分布乘法计数原理，共有： ••（•）•=24种方法；‎ ‎②四次考试都选，有两次考两科，另外两次各考一科，共=6种方法；分别为方案2211，2121，2112，1221，1212，1122．‎ 若为2211，第一次有种方法，‎ 第二次有两种情况，1°选考过的两科，有种方法，则第三次只考剩下的第三科有1种方法；第四次只有1种方法，故共有••1•1=3种方法；‎ ‎2°剩下的一科与考过的两科中的一科，有•种方法，则第三次与第四次共有种方法，故共有•••=12种方法；‎ 综上所述，2211方案共有15种方法；‎ 若方案为2121，共有（••+••）=15种方法；‎ 若方案为2112，共有（••+••）=15种方法；‎ 同理可得，另外3种情况，每种各有15种方法，‎ 所以，四次考试都选，共有15×6=90种方法．‎ 综合①②得：共有24+90=114种方法．‎ 故答案为：114．‎ ‎　‎ ‎16．如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，P，Q，R分别是棱AB，AD，AA1的中点．以△‎ PQR为底面作一个直三棱柱，使其另一个底面的三个顶点也都在此正方体的表面上．则这个直三棱柱的体积是　　．‎ ‎【考点】LF：棱柱、棱锥、棱台的体积．‎ ‎【分析】该直三棱柱的另一底面三个顶点分别是面A1B1C1D1、面DD1C1C、面BB1C1C的中心，记为M、N、H，则三这个棱柱的高h=PH=RM=QN，求解三角形求得高和底面积，代入柱体体积公式得答案．‎ ‎【解答】解：∵正方体ABCD﹣A1B1C1D1的棱长为1，P，Q，R分别是棱AB，AD，AA1的中点，‎ 以△PQR为底面作直三棱柱（侧棱与底面垂直的三棱柱叫直三棱柱），‎ ‎∴该直三棱柱的另一底面三个顶点分别是面A1B1C1D1、面DD1C1C、面BB1C1C的中心，记为M、N、H，‎ 则三这个棱柱的高h=PH=RM=QN，‎ 这个三棱柱的高h=RM==．‎ 底面正三角形PQR的边长为，面积为=．‎ ‎∴这个直三棱柱的体积是．‎ 故答案为：．‎ ‎　‎ ‎17．函数y=ax2﹣2x的图象上有且仅有两个点到直线y=x的距离等于，则实数a的取值集合是　{a|a＜﹣或a=0或a}　．‎ ‎【考点】3W：二次函数的性质．‎ ‎【分析】对a进行分类讨论，得出y=ax2﹣2x与y=x±2的位置关系，根据交点个数判断a的范围．‎ ‎【解答】解：（1）若a=0，则y=2x与y=x为相交直线，‎ 显然y=2x上存在两点到y=x的距离等于，符合题意；‎ ‎（2）若a＞0，则y=ax2﹣2x与直线y=x相交，‎ ‎∴y=ax2﹣2x在直线y=x上方的图象必有2点到直线y=x的距离等于，‎ 又直线y=x与y=x﹣2的距离为，‎ ‎∴抛物线y=ax2﹣2x与直线y=x﹣2不相交，‎ 联立方程组，消元得ax2﹣3x+2=0，‎ ‎∴△=9﹣8a＜0，解得a．‎ ‎（3）若a＜0，同理可得a＜﹣．‎ 故答案为：{a|a＜﹣或a=0或a}．‎ ‎　‎ 三．解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.‎ ‎18．设函数f（x）=sin2ωx﹣cos2ωx+2sinωxcosωx+λ的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（，1）．‎ ‎（Ⅰ）求函数f（x）的最小正周期；‎ ‎（Ⅱ）若y=f（x）的图象经过点（，0），求函数f（x）在区间[0，]上的取值范围．‎ ‎【考点】GL：三角函数中的恒等变换应用；H2：正弦函数的图象．‎ ‎【分析】（Ⅰ）先利用二倍角公式和两角差的余弦公式将函数f（x）化为y=Asin（ωx+φ）+k型函数，再利用函数的对称性和ω的范围，计算ω的值，最后利用周期计算公式得函数的最小正周期；‎ ‎（Ⅱ）先将已知点的坐标代入函数解析式，求得λ的值，再利用正弦函数的图象和性质即可求得函数f（x）的范围即可．‎ ‎【解答】解：（Ⅰ）f（x）=sin2ωx+2sinωx•cosωx﹣cos2ωx+λ ‎=sin2ωx﹣cos2ωx+λ ‎=2sin（2ωx﹣）+λ，‎ ‎∵图象关于直线x=π对称，∴2πω﹣=+kπ，k∈z．‎ ‎∴ω=+，又ω∈（，1），‎ 令k=1时，ω=符合要求，‎ ‎∴函数f（x）的最小正周期为=；‎ ‎（Ⅱ）∵f（）=0，‎ ‎∴2sin（2××﹣）+λ=0，‎ ‎∴λ=﹣，‎ ‎∴f（x）=2sin（x﹣）﹣，‎ ‎∴f（x）∈[﹣1﹣，2﹣]．‎ ‎　‎ ‎19．在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O′的直径，FB是圆台的一条母线．‎ ‎（I）已知G，H分别为EC，FB的中点，求证：GH∥平面ABC；‎ ‎（Ⅱ）已知EF=FB=AC=2，AB=BC，求二面角F﹣BC﹣A的余弦值．‎ ‎【考点】MT：二面角的平面角及求法；LS：直线与平面平行的判定．‎ ‎【分析】（Ⅰ）取FC中点Q，连结GQ、QH，推导出平面GQH∥平面ABC，由此能证明GH∥平面ABC．‎ ‎（Ⅱ）由AB=BC，知BO⊥AC，以O为原点，OA为x轴，OB为y轴，OO′为z轴，建立空间直角坐标系，利用向量法能求出二面角F﹣BC﹣A的余弦值．‎ ‎【解答】证明：（Ⅰ）取FC中点Q，连结GQ、QH，‎ ‎∵G、H为EC、FB的中点，‎ ‎∴GQ，QH，‎ 又∵EF∥BO，∴GQ∥BO，‎ ‎∴平面GQH∥平面ABC，‎ ‎∵GH⊂面GQH，∴GH∥平面ABC．‎ 解：（Ⅱ）∵AB=BC，∴BO⊥AC，‎ 又∵OO′⊥面ABC，‎ ‎∴以O为原点，OA为x轴，OB为y轴，OO′为z轴，建立空间直角坐标系，‎ 则A（，0，0），C（﹣2，0，0），B（0，2，0），O′（0，0，3），F（0，，3），‎ ‎=（﹣2，﹣，﹣3），=（2，2，0），‎ 由题意可知面ABC的法向量为=（0，0，3），‎ 设=（x0，y0，z0）为面FCB的法向量，‎ 则，即，‎ 取x0=1，则=（1，﹣1，﹣），‎ ‎∴cos＜，＞==﹣．‎ ‎∵二面角F﹣BC﹣A的平面角是锐角，‎ ‎∴二面角F﹣BC﹣A的余弦值为．‎ ‎　‎ ‎20．已知函数f（x）=+x（a，b∈R）．‎ ‎（Ⅰ）当a=2，b=3时，求函数f（x）极值；‎ ‎（Ⅱ）设b=a+1，当0≤a≤1时，对任意x∈[0，2]，都有m≥|f'（x）|恒成立，求m的最小值．‎ ‎【考点】6E：利用导数求闭区间上函数的最值；6D：利用导数研究函数的极值．‎ ‎【分析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可；‎ ‎（Ⅱ）对a进行分类讨论：当a=0时，f（x）=﹣x+1，m≥1；再对对称轴进行讨论，当＜2时，即a＞；当≥2时，即a≤，分别去求|f（x）|的最大值．‎ ‎【解答】解：（Ⅰ）a=2，b=3时，f（x）=x3﹣x2+x，‎ f′（x）=2x2﹣3x+1=（2x﹣1）（x﹣1），‎ 令f′（x）＞0，解得：x＞1或x＜，‎ 令f′（x）＜0，解得：＜x＜1，‎ 故f（x）在（﹣∞，）递增，在（，1）递减，在（1，+∞）递增，‎ 故f（x）极大值=f（）=，f（x）极小值=f（1）=，‎ ‎（Ⅱ）当b=a+1，f（x）=ax3﹣（a+1）x2+x，‎ f′（x）=ax2﹣（a+1）x+1，f′（x）恒过点（0，1）；‎ 当a=0时，f′（x）=﹣x+1，‎ m≥|f′（x）|恒成立，‎ ‎∴m≥1；‎ ‎0＜a≤1，开口向上，对称轴≥1，‎ f′（x）=ax2﹣（a+1）x+1=a（x﹣）2+1﹣，‎ ‎①当a=1时f′（x）=x2﹣2x+1，|f′（x）|在x∈[0，2]的值域为[0，1]；‎ 要m≥|f′（x）|，则m≥1；‎ ‎②当0＜a＜1时，‎ 根据对称轴分类：‎ 当x=＜2，即＜a＜1，‎ ‎△=（a﹣1）2＞0，‎ f′（）=﹣（a+）∈（﹣，0），又f′（2）=2a﹣1＜1，所以|f′（x）|≤1；‎ 当x=≥2，即0＜a≤；‎ f′（x）在x∈[0，2]的最小值为f′（2）=2a﹣1；‎ ‎﹣1＜2a﹣1≤﹣，所以|f′（x）|≤1，‎ 综上所述，要对任意x∈[0，2]都有m≥|f′（x）|恒成立，有m≥1，‎ ‎∴m≥1．‎ ‎　‎ ‎21．已知椭圆+y2=1（a＞1），过直线l：x=2上一点P作椭圆的切线，切点为A，当P点在x轴上时，切线PA的斜率为±．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设O为坐标原点，求△POA面积的最小值．‎ ‎【考点】K4：椭圆的简单性质．‎ ‎【分析】（Ⅰ）由P在x轴设出P点坐标及直线PA方程，将PA方程与椭圆方程联立，整理关于x的一元二次方程，△=0求得a2，即可求得椭圆方程；‎ ‎（Ⅱ）设出切线方程和点P及点A的坐标，将切线方程代入椭圆方程，求得关于x的一元二次方程，△=0，求得A和P点的坐标，求得丨PO丨及A到直线OP的距离，根据三角形的面积公式求得S=丨k+丨，平方整理关于k的一元二次方程，△≥0，即可求得S的最小值．‎ ‎【解答】解：（1）当P点在x轴上时，P（2，0），PA：，‎ ‎，‎ ‎△=0⇒a2=2，椭圆方程为；…﹣5‎ ‎（2）设切线为y=kx+m，设P（2，y0），A（x1，y1），‎ 则⇒（1+2k2）x2+4kmx+2m2﹣2=0⇒△=0⇒m2=2k2+1，…7‎ 且，y0=2k+m 则，‎ PO直线为，A到直线PO距离，…﹣10‎ 则 ‎=，…13‎ ‎∴（S﹣k）2=1+2k2⇒k2+2Sk﹣S2+1=0，‎ ‎，此时．…﹣15‎ ‎　‎ ‎22．已知函数fn（x）=xn（1﹣x）2在（，1）上的最大值为an（n=1，2，3，…）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）求证：对任何正整数n（n≥2），都有an≤成立；‎ ‎（3）设数列{an}的前n项和为Sn，求证：对任意正整数n，都有Sn＜成立．‎ ‎【考点】8E：数列的求和；8H：数列递推式．‎ ‎【分析】（1）由已知得=（n+2）xn﹣1（x﹣1）（x﹣），由此利用导数性质能求出数列{an}的通项公式．‎ ‎（2）当n≥2时，欲证≤，只需证明（1+）n≥4，由此能证明当n≥2时，都有成立． ‎ ‎（3）Sn＜＜，由此能证明任意正整数n，都有成立．‎ ‎【解答】解：（1）∵fn（x）=xn（1﹣x）2，‎ ‎∴‎ ‎=xn﹣1（1﹣x）[n（1﹣x）﹣2x]‎ ‎=（n+2）xn﹣1（x﹣1）（x﹣），…‎ 当x∈（，1）时，由，知：x=，…‎ ‎∵n≥1，∴，…‎ ‎∵x∈（，）时，；x∈（）时，（x）＜0；‎ ‎∴f（x）在（）上单调递增，在（）上单调递减 ‎∴在x=处取得最大值，‎ 即=．…‎ ‎（2）当n≥2时，欲证≤，‎ 只需证明（1+）n≥4，…‎ ‎∵（1+）n=‎ ‎≥1+2+≥1+2+1=4，…‎ ‎∴当n≥2时，都有成立． …‎ ‎（3）Sn=a1+a2+…+an ‎＜‎ ‎＜‎ ‎=＜．‎ ‎∴对任意正整数n，都有成立．…‎