中山市2013年高考数学模拟试题目文新人民教育出版 14页

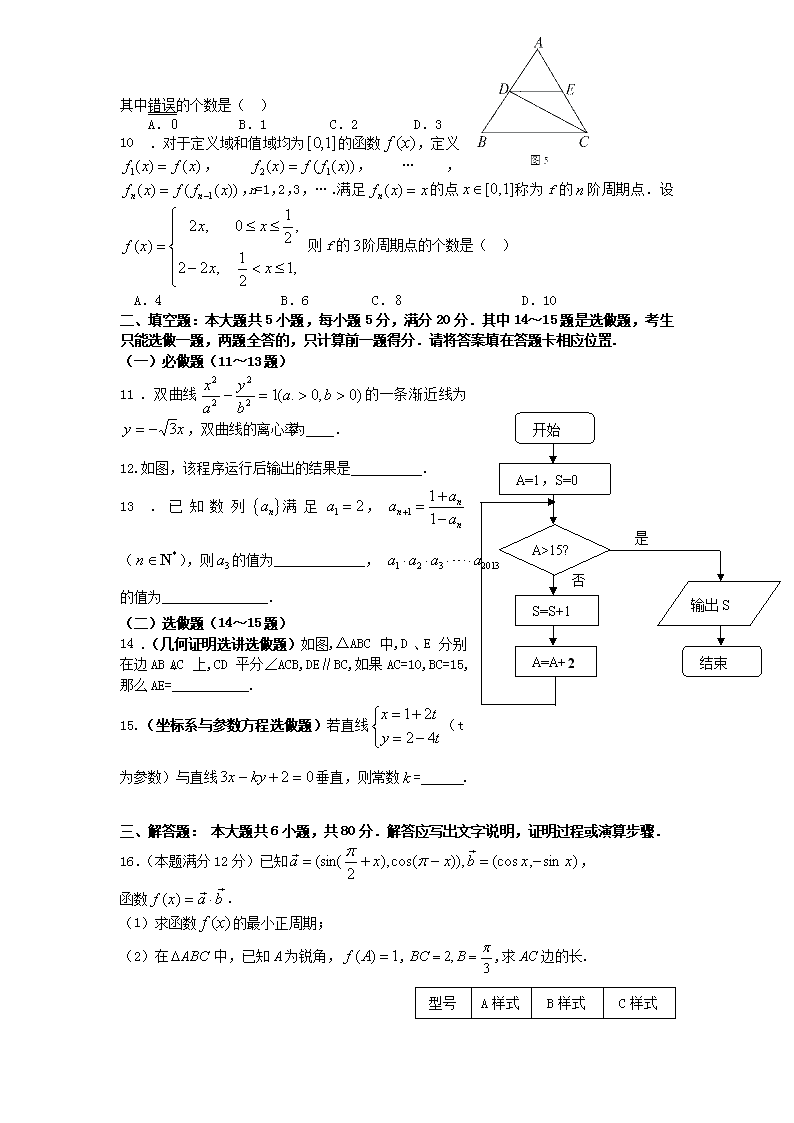
中山2013年高考文数模拟试题 一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 已知复数的实部是，虚部是，其中为虚数单位，则在复平面对应的点在（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎ ‎2. 数列是等差数列，是它的前项和，若那么= ‎ A．43 B．‎54 C．48 D．56 ‎ ‎3.“”是“直线：和圆:相切”的（ ）‎ ‎ A.充分不必要条件 B.必要不充分条件 ‎ C.充要条件 D.既不充分也不必要条件 ‎4. 如图，某几何体的正视图和俯视图都是矩形，侧视图是等腰直角三角形，则该几何体的体积为 （ ）‎ A． B． C． D． ‎ ‎5．如图，在中，已知，则 （ ）‎ A. B. ‎ C. D. ‎ ‎6.若若（ ）‎ ‎ A． B． C. D． 或 ‎7.已知，若不等式恒成立，则的最大值等于（ ）‎ A.4 B‎.16 C.9 D.3‎ ‎8.函数，函数的零点所在的区间是()，则的值等于 （ ）‎ ‎ A. B. C. D. 或 ‎9．有下列四种说法：‎ ‎ ①命题“”的否定是“” ；‎ ‎ ②“命题为真”是“命题为真”的必要不充分条件；‎ ‎③“若”的逆命题为真；‎ ‎④若实数,则满足: 的概率为.‎ 其中错误的个数是（ ）‎ A． B．‎1 ‎C．2 D．3‎ ‎10．对于定义域和值域均为的函数，定义，，…，，n=1，2，3，…．满足的点称为f的阶周期点．设 则f的阶周期点的个数是（ ）‎ A．4 　　　　 　　B．‎6 C． 　　　　　　 D．10‎ 二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置.‎ ‎（一）必做题（11～13题）‎ ‎11．双曲线的一条渐近线为，双曲线的离心率为　　． ‎ A=1，S=0‎ S=S+1‎ A=A+2‎ A>15?‎ 输出S 结束 开始 否 是 ‎12.如图，该程序运行后输出的结果是 ． ‎ ‎13．已知数列满足，（），则的值为 ， 的值为 ．‎ ‎（二）选做题（14～15题）‎ ‎14．（几何证明选讲选做题）如图,△ABC中,D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,如果AC=10,BC=15,那么AE=___________. ‎ ‎15.（坐标系与参数方程选做题）若直线（t为参数）与直线垂直，则常数= . ‎ 三、解答题： 本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．‎ ‎16．（本题满分12分）已知，‎ 函数. ‎ ‎（1）求函数的最小正周期；‎ ‎（2）在中，已知为锐角，,,求边的长. ‎ 型号 A样式 B样式 C样式 ‎10W ‎2000‎ z ‎3000‎ ‎30W ‎3000‎ ‎4500‎ ‎5000‎ ‎17．(本小题满分12分)‎ 一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个):‎ 按样式分层抽样的方法在这个月生产的灯泡中抽取100个，其中有A样式灯泡25个. （1）求z的值； ‎ ‎（2）用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本，从这个样本中任取2个灯泡，求至少有1个10W的概率．‎ ‎18.(本小题满分14分) 矩形中，，是中点，沿将折起到的位置，使，分别是中点.‎ ‎（1）求证：⊥；‎ ‎（2）设，求四棱锥的体积. ‎ ‎19. (本小题满分14分) 在平面直角坐标系上，设不等式组表示的平面区域为，记内的整点（横坐标和纵坐标均为整数的点）的个数为.‎ ‎（1）求出的值（不要求写过程）；‎ ‎（2）求数列的通项公式；‎ ‎（3）令bn=（n∈N*），求b1+b2+…+bn.‎ ‎20．（本小题满分14分）已知函数．‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）若对于任意都有成立，求实数的取值范围；‎ ‎（3）若过点可作函数图象的三条不同切线，求实数的取值范围．‎ ‎21．（本小题满分14分） 已知椭圆的左焦点为,‎ 离心率e=,M、N是椭圆上的的动点。‎ ‎（Ⅰ）求椭圆标准方程；‎ ‎（Ⅱ）设动点P满足：，直线OM与ON的斜率之积为，问：是否存在定点，使得为定值？，若存在，求出的坐标，若不存在，说明理由。‎ ‎（Ⅲ）若在第一象限，且点关于原点对称，点在轴上的射影为，连接 并延长交椭圆于点，证明：；‎ 中山2013年高考文数模拟试题答题卷 ‎ 班级 姓名 登分号 ‎ 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 二、填空题 ‎11. 12. 13. ; ‎ ‎14. 15. ‎ 三、解答题： 本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．‎ ‎16．（本题满分12分）‎ ‎17．(本小题满分12分)‎ ‎18.(本小题满分14分)‎ ‎19. (本小题满分14分)‎ ‎20．（本小题满分14分）已知函数．‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）若对于任意都有成立，求实数的取值范围；‎ ‎（3）若过点可作函数图象的三条不同切线，求实数的取值范围．‎ ‎21．（本小题满分14分） 已知椭圆的左焦点为,离心率e=,M、N是椭圆上的的动点。‎ ‎（Ⅰ）求椭圆标准方程；‎ ‎（Ⅱ）设动点P满足：，直线OM与ON的斜率之积为，问：是否存在定点，使得为定值？，若存在，求出的坐标，若不存在，说明理由。‎ ‎（Ⅲ）若在第一象限，且点关于原点对称，点在轴上的射影为，连接 并延长交椭圆于点，证明：；‎ 中山2013年高考文数模拟试题参考答案及评分标准 一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.‎ ‎1. C 2. D 3. A 4. B 5. C 6．C 7．B 8．B 9. B 10．C 二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置.‎ ‎11． 2; 12．8 ; 13. (2分) （3分） ; 14.4 ; 15. 6‎ 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．‎ ‎16．（本题满分12分）已知，‎ 函数. ‎ ‎（1）求函数的最小正周期；‎ ‎（2）在中，已知为锐角，,,求边的长.‎ ‎16 解： (1) 由题设知（2分）‎ ‎……4分 …6分 ‎(2) ‎ ‎ ……………………8分 ‎ ‎ ‎……………………………12分 ‎17．(本小题满分12分)‎ 一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个):‎ 按样式分层抽样的方法在这个月生产的灯泡中抽取100个，其中有A样式灯泡25个. （1）求z的值； ‎ ‎（2）用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本，从这个样本中任取2个灯泡，求至少有1个10W的概率．‎ 型号 A样式 B样式 C样式 ‎10W ‎2000‎ z ‎3000‎ ‎17解: (1).设该厂本月生产的B样式的灯泡为n个,在C样式的灯泡中抽取x个，由题意得, ‎ ‎,‎ 所以x=40. -----------2分 则100－40－25＝35，‎ 所以，n=7000， 故z＝2500 ------6分 ‎(2) 设所抽样本中有m个10W的灯泡,‎ 因为用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,‎ 所以,解得m=2 -----------8分 也就是抽取了2个10W的灯泡,3个30W的灯泡,‎ 分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事件为 ‎(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)‎ 共10个, （10分）‎ 其中至少有1个10W的灯泡的基本事件有7个基本事件: （11分）‎ ‎ (S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2个,‎ 至少有1个10W的灯泡的概率为. -----------12分 ‎18.(本小题满分14分) 矩形中，，是中点，沿将折起到的位置，使，分别是中点.‎ ‎（1）求证：⊥；‎ ‎（2）设，求四棱锥的体积. ‎ ‎18（1）证明：矩形中，∵分别是、中点 ‎ 1分 ‎ 2 分 ‎ ∵ 3 分 ‎ 4 分 平面 6 分 又平面7分 ‎8 分 ‎（2）∵‎ ‎，‎ 在等腰直角三角形中，且 9分 ‎∵且、不平行 平面 10分 几何体的体积 ‎ 14分 ‎19. (本小题满分14分) 在平面直角坐标系上，设不等式组表示的平面区域为，记内的整点（横坐标和纵坐标均为整数的点）的个数为.‎ ‎（1）求出的值（不要求写过程）；（2）求数列的通项公式；‎ ‎（3）令bn=（n∈N*），求b1+b2+…+bn.‎ ‎19. 解：（1） ………………3分 ‎（2）由 得 …………4分 所以平面区域为内的整点为点（3,0）与在直线上，…………5分 直线与直线交点纵坐标分别为……6分 内在直线上的整点个数分别为4n+1和2n+1, …………………9分 ‎（3）∵bn= ……………10分 b1+b2+…+bn ‎ ………………………14分 ‎20．（本小题满分14分）已知函数．‎ ‎（1）当时，求函数的单调区间；‎ ‎（2）若对于任意都有成立，求实数的取值范围；‎ ‎（3）若过点可作函数图象的三条不同切线，求实数的取值范围．‎ ‎20．解：（1）当时，，得．…1分 因为，‎ 所以当时，，函数单调递增；‎ 当或时，，函数单调递减．‎ 所以函数的单调递增区间为，单调递减区间为和．………4分 ‎（2）方法1：由，得，‎ 因为对于任意都有成立，‎ 即对于任意都有成立，‎ 即对于任意都有成立，…………6分 令，‎ 要使对任意都有成立， ‎ 必须满足 或 ………………………………………………8分 ‎ 即 或 ………………………………9分 所以实数的取值范围为．………………………10分 方法2：由，得，‎ 因为对于任意都有成立，‎ 所以问题转化为，对于任意都有．………6分 因为，其图象开口向下，对称轴为．‎ ‎①当时，即时，在上单调递减， ‎ 所以，‎ 由，得，此时．………………7分 ‎②当时，即时，在上单调递增，在上单调递减，‎ 所以，‎ 由，得，此时．……8分 综上①②可得，实数的取值范围为．……………10分 ‎（3）设点是函数图象上的切点，‎ 则过点的切线的斜率为，‎ 所以过点的切线方程为．………11分 因为点在切线上，‎ 所以，‎ 即．……………12分 若过点可作函数图象的三条不同切线，‎ 则方程有三个不同的实数解．……………13分 令，则函数与轴有三个不同的交点．‎ 令，解得或．‎ 因为，，‎ 所以必须，即．‎ 所以实数的取值范围为．……………14分 ‎21．（本小题满分14分） 已知椭圆的左焦点为,离心率e=,M、N是椭圆上的的动点。‎ ‎（Ⅰ）求椭圆标准方程；‎ ‎（Ⅱ）设动点P满足：，直线OM与ON的斜率之积为，问：是否存在定点，使得为定值？，若存在，求出的坐标，若不存在，说明理由。‎ ‎（Ⅲ）若在第一象限，且点关于原点对称，点在轴上的射影为，连接 并延长交椭圆于点，证明：；‎ ‎21.解：（Ⅰ）由题设可知：……………………………2分 ‎ 故……………………………3分 ‎ 故椭圆的标准方程为：……………………………4分 ‎（Ⅱ）设，由可得：‎ ‎……………………………5分 由直线OM与ON的斜率之积为可得：‎ ‎ ，即……………………………6分 ‎ 由①②可得：‎ ‎ M、N是椭圆上，故 ‎ 故，即……………..8分 ‎ 由椭圆定义可知存在两个定点，使得动点P到两定点距离和为定值;……………………………….9分；‎ ‎（Ⅲ）设 ‎ 由题设可知……10分 ‎ 由题设可知斜率存在且满足………….③‎ ‎ …………………12分 ‎ 将③代入④可得：‎ ‎……⑤……13分 ‎ 点在椭圆，故 所以…………14分