线线角线面角二面角高考立体几何法宝 8页

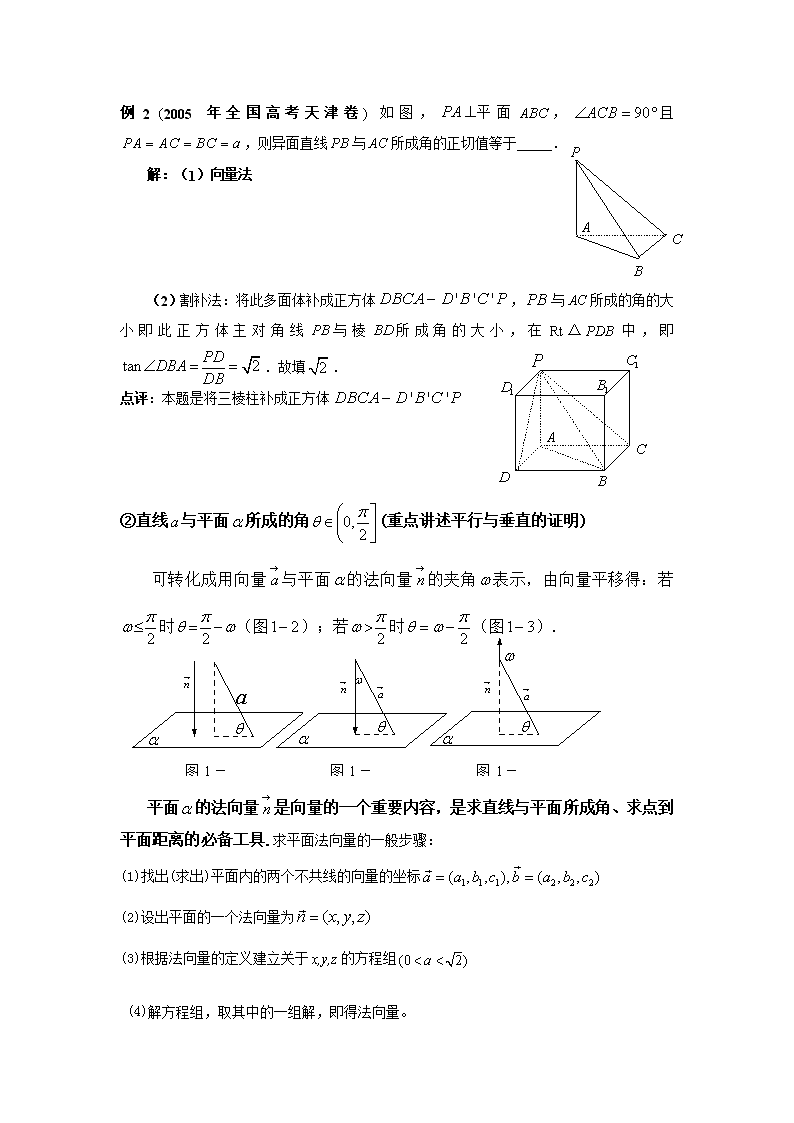
线线角、线面角、二面角的求法 1. 空间向量的直角坐标运算律：‎ ‎⑴两个非零向量与垂直的充要条件是 ‎⑵两个非零向量与平行的充要条件是 ‎·=±||||‎ ‎2.向量的数量积公式 若与的夹角为θ(0≤θ≤π),且，,则 ‎（1）点乘公式： ·=|||| cosθ ‎ ‎（2）模长公式：则，‎ ‎（3）夹角公式：‎ ‎（4）两点间的距离公式：若，，则 ‎， ‎ ‎①两条异面直线、间夹角 在直线上取两点A、B，在直线上取两点C、D，若直线与的夹角为，则。‎ 例1 (福建卷)如图，长方体ABCD—A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是（ ）‎ ‎ A． B．‎ C． D． ‎ ‎（向量法，传统法）‎ 例2 (2005年全国高考天津卷)如图，平面，且，则异面直线PB与AC所成角的正切值等于_____．‎ 解：（1）向量法 ‎（2）割补法：将此多面体补成正方体，与所成的角的大小即此正方体主对角线与棱所成角的大小，在Rt△PDB中，即．故填．‎ 点评：本题是将三棱柱补成正方体 ‎②直线与平面所成的角(重点讲述平行与垂直的证明)‎ 图1－2‎ 图1－1‎ 图1－3‎ 可转化成用向量与平面的法向量的夹角表示，由向量平移得：若时（图）；若时（图）.‎ 平面的法向量是向量的一个重要内容，是求直线与平面所成角、求点到平面距离的必备工具.求平面法向量的一般步骤：‎ ‎(1)找出(求出)平面内的两个不共线的向量的坐标 ‎(2)设出平面的一个法向量为 ‎(3)根据法向量的定义建立关于x,y,z的方程组 ‎ ‎ ‎ (4)解方程组，取其中的一组解，即得法向量。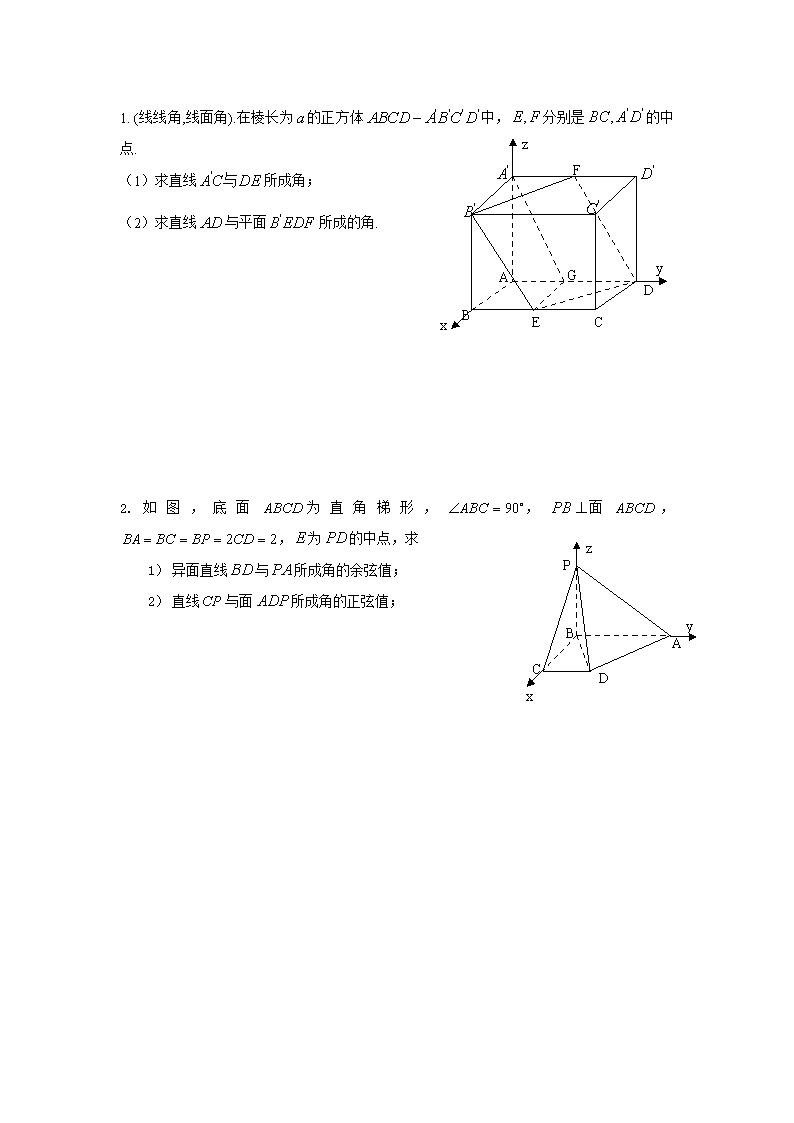‎ A B C D E F G x y z ‎1. (线线角,线面角).在棱长为的正方体中，分别是的中点.‎ ‎（1）求直线所成角；‎ ‎（2）求直线与平面所成的角.‎ B C D P A x y z ‎2.如图，底面为直角梯形，，面，，为的中点，求 1） 异面直线与所成角的余弦值；‎ 2） 直线与面所成角的正弦值；‎ ‎③求二面角的大小 ‎1.范围：‎ ‎2.二面角的向量求法：‎ ‎ 方法一：如图，若AB、CD分别是二面角α-l-β的两个面内与棱l垂直的异面直线,则二面角的大小就是向量与的夹角. ‎ β l α ‎ 方法二:设是二面角α-l-β的两个面α,β的法向量,则向量与的夹角(或其补角就是二面角的平面角的大小.如图,设二面角的平面角的大小为,法向量的夹角为.‎ ‎ ‎ ‎ ‎ ‎ 注意:在用向量求二面角的大小时，我们是先求出两半平面的法向量所在直线的夹角，但二面角可能是钝角或锐角，因此在求出角后，应判断二面角的大小，再确定二面角就是两半平面的法向量所在直线的夹角或是其补角。‎ A B C P D E x y z 例：如图，，，求二面角的大小。‎ ‎1.[2014·新课标全国卷Ⅱ] 如图，四棱锥P ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．‎ ‎(1)证明：PB∥平面AEC；‎ ‎(2)设AP＝1，AD＝，三棱锥P ABD的体积V＝，求A到平面PBC的距离．‎ ‎2、(2011年高考陕西卷理科16)（本小题满分12分）‎ 如图：在，沿把折起，使.证明：‎ ‎（Ⅰ）平面；‎ ‎（Ⅱ）设。‎ ‎3、(2011年高考北京卷理科16)（本小题共14分）‎ ‎ 如图，在四棱锥中，平面，底面是菱形，.‎ ‎(Ⅰ)求证：平面 （Ⅱ）若求与所成角的余弦值；‎ ‎ ‎ ‎4、(2011年高考全国新课标卷理科18) (本小题满分12分)‎ 如图，四棱锥P—ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.‎ ‎(Ⅰ)证明：PA⊥BD；‎ ‎(Ⅱ)若PD=AD，求二面角A-PB-C的余弦值。‎ 直线与平面平行或者垂直（重点掌握）‎ A B C D A111‎ B11‎ C11111‎ D1111‎ M N ‎1.如图，已知正方体ABCD-A1B1C1D1，M,N分别是A1B1，BB1的中点.求证:‎ ‎(1)MN//平面ACD1 ; (2)DB1⊥平面ACD1. ‎ ‎2、如图，四棱锥P—ABCD中， PA平面ABCD，底面ABCD是直角梯形，AB⊥AD，CD⊥AD，CD=2AB，E为PC中点．‎ A B C D E P ‎ (I) 求证：CD平面PAD；‎ ‎ (II) 求证：BE//平面PAD． ‎ ‎3.正方体ABCD—A1B1C1D1中O为正方形ABCD的中心，M为BB1的中点，求证：‎ （1） D1O//平面A1BC1;‎ ‎ （2）D1O⊥平面MAC.‎ ‎4.如图, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AA1＝4，,点D是AB的中点，求证： ‎ ‎（I）AC⊥BC1； （II）A1C //平面CDB1；‎ ‎5.已知正方体ABCD－A1B1C1D1的棱长为2，E、F、G分别是BB1、DD1、DC的中点，求证：‎ (1) 平面ADE∥平面B1C1F；‎ ‎(2)平面ADE⊥平面A1D1G； ‎