理科数学高考立体几何大题精选 7页

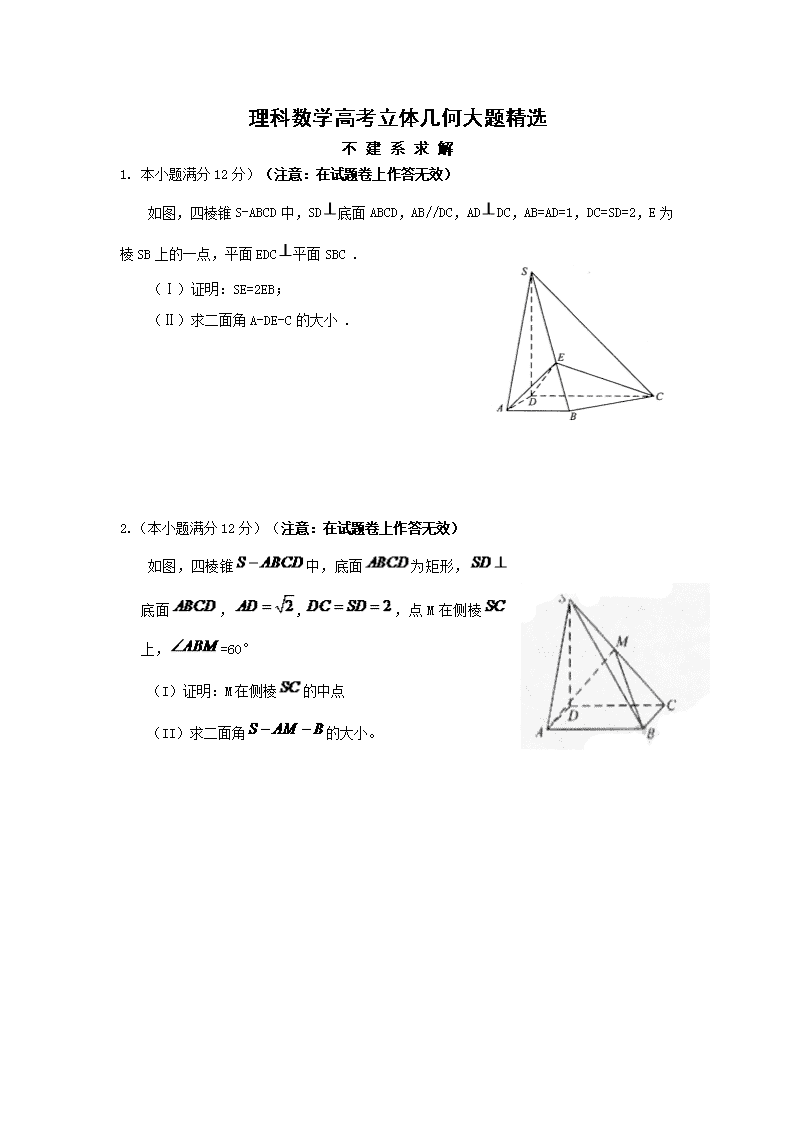
‎ 理科数学高考立体几何大题精选 不 建 系 求 解 ‎1. 本小题满分12分）（注意：在试题卷上作答无效）‎ 如图，四棱锥S-ABCD中，SD底面ABCD，AB//DC，ADDC，AB=AD=1，DC=SD=2，E为棱SB上的一点，平面EDC平面SBC .‎ ‎（Ⅰ）证明：SE=2EB；‎ ‎（Ⅱ）求二面角A-DE-C的大小 .‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎2.（本小题满分12分）（注意：在试题卷上作答无效）‎ 如图，四棱锥中，底面为矩形，底面，,，点M在侧棱上，=60°‎ ‎（I）证明：M在侧棱的中点 ‎（II）求二面角的大小。‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 3．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.‎ ‎(I)求证:‎ ‎(II)‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎4．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））如图,四棱锥中,,,为的中点,.‎ ‎(1)求的长; (2)求二面角的正弦值.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎5．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD版））如图,在四面体中,平面,.是的中点, 是的中点,点在线段上,且.‎ ‎(1)证明:平面;(2)若二面角的大小为,求的大小.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎6．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD版））如图1,在等腰直角三角形中,,,分别是上的点,,‎ 为的中点.将沿折起,得到如图2所示的四棱锥,其中.‎ ‎(Ⅰ) 证明:平面; (Ⅱ) 求二面角的平面角的余弦值.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎7．（2013年高考陕西卷（理））如图, 四棱柱ABCD-A1B‎1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, . ‎ ‎(Ⅰ) 证明: A‎1C⊥平面BB1D1D; ‎ ‎(Ⅱ) 求平面OCB1与平面BB1D1D的夹角的大小. ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎8．（2013年高考四川卷（理））如图,在三棱柱中,侧棱底面,,,分别是线段的中点,是线段的中点.‎ ‎(Ⅰ)在平面内,试作出过点与平面平行的直线,说明理由,并证明直线平面;‎ ‎(Ⅱ)设(Ⅰ)中的直线交于点,交于点,求二面角的余弦值.‎ ‎ ‎ ‎ ‎ ‎9．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））本小题满分10分.‎ 如图,在直三棱柱中,,,,点是的中点 ‎(1)求异面直线与所成角的余弦值 ‎(2)求平面与所成二面角的正弦值.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎10．（2013年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））如图,四棱锥中,与都是等边三角形.‎ ‎(I)证明: (II)求二面角的大小.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎11．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））如图所示,在三棱锥中,平面,, 分别是的中点, ,与交于点,与交于点,连接.‎ ‎(Ⅰ)求证:; (Ⅱ)求二面角的余弦值.‎ ‎ ‎ ‎ ‎ ‎12．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD版含答案））如图,直棱柱中,分别是的中点,.‎ ‎(Ⅰ)证明:平面; (Ⅱ)求二面角的正弦值.‎ ‎ ‎ ‎ ‎ ‎13．（2013年高考北京卷（理））如图,在三棱柱ABC-A1B‎1C1中,AA‎1C1C是边长为4的正方形,平面ABC⊥平面AA‎1C1C,AB=3,BC=5.‎ ‎(Ⅰ)求证:AA1⊥平面ABC;‎ ‎(Ⅱ)求二面角A1-BC1-B1的余弦值;‎ ‎(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值.‎ ‎ ‎ ‎ ‎