浙江高考数学试题有答案解析 17页

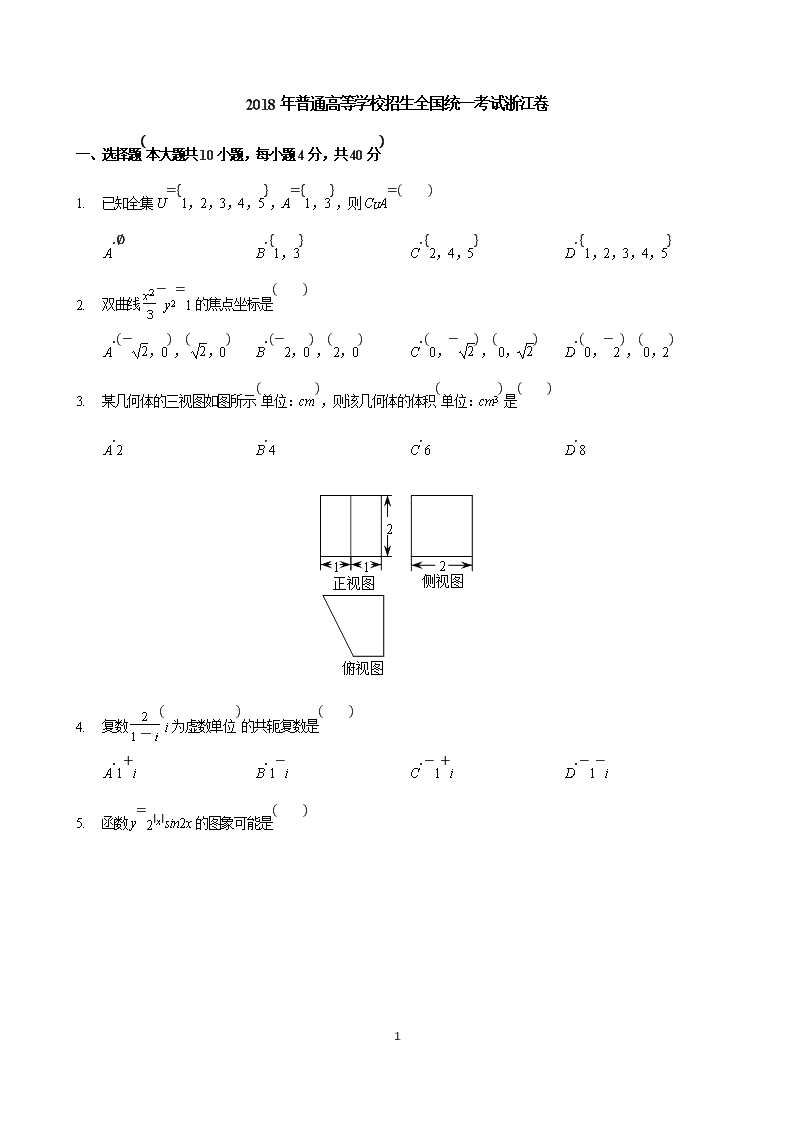
‎2018年普通高等学校招生全国统一考试浙江卷 一、选择题(本大题共10小题，每小题4分，共40分)‎ 1. 已知全集U={1，2，3，4，5}，A={1，3}，则CUA=( )‎ A. ∅ B. {1，3} C. {2，4，5} D. {1，2，3，4，5}‎ 2. 双曲线‎ ‎x‎2‎‎3‎−y2=1的焦点坐标是( )‎ A. (−‎2‎，0)，(‎2‎，0) B. (−2，0)，(2，0) C. (0，−‎2‎)，(0，‎2‎) D. (0，−2)，(0，2)‎ 3. 某几何体的三视图如图所示(单位：cm)，则该几何体的体积(单位：cm3)是( )‎ A. 2 B. 4 C. 6 D. 8‎ 4. 复数‎ ‎‎2‎‎1-i(i为虚数单位)的共轭复数是( )‎ A. 1+i B. 1−i C. −1+i D. −1−i 5. 函数y=‎2‎‎|x|‎sin2x的图象可能是( )‎ 17‎ 1. 已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的( )‎ A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 2. 设01，则( )‎ A. a1a3，a2a4 D. a1>a3，a2>a4‎ 17‎ 二、填空题(本大题共7小题，多空题每题6分，单空题每题4分，共36分)‎ 1. 我国古代数学著作《张邱建算经》中记载百鸡问题：“今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一，凡百钱，买鸡百只，问鸡翁、母、雏各几何？”设鸡翁、鸡母，鸡雏个数分别为x，y，z，则x+y+z=100 ‎‎5x+3y+‎1‎‎3‎z=100‎，当z=81时，x=__________________________，y=___________________________‎ 2. 若x，y满足约束条件x-y≥0‎‎2x+y≤6‎x+y≥2 ‎，则z=x+3y的最小值是________________________，最大值是_____________________‎ 3. 在△ABC中，角A，B，C所对的边分别为a，b，c，若a=‎7‎，b=2，A=60°，则sinB=_________________，c=___________________‎ 4. 二项式(‎3‎x+‎ ‎‎1‎‎2x)8的展开式的常数项是_________________________‎ 5. 已知λ∈R，函数f(x)=x-4，x≥λ ‎x‎2‎‎-4x+3，x<λ，当λ=2时，不等式f(x)<0的解集是_____________________，若函数f(x)恰有2个零点，则λ的取值范围是________________________‎ 6. 从1，3，5，7，9中任取2个数字，从0，2，4，6中任取2个数字，一共可以组成______________________个没有重复数字的四位数(用数字作答)‎ 7. 已知点P(0，1)，椭圆‎ ‎x‎2‎‎4‎+y2=m(m>1)上两点A，B满足AP=2PB，则当m=____________________时，点B横坐标的绝对值最大 三、解答题(本大题共5小题，共74分)‎ 8. ‎(14分)已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P(−‎ ‎‎3‎‎5‎，−‎ ‎‎4‎‎5‎)‎ (1) 求sin(α+π)的值 (2) 若角β满足sin(α+β)=‎ ‎‎5‎‎13‎，求cosβ的值 17‎ 1. ‎(15分)如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2‎ (1) 证明：AB1⊥平面A1B1C1‎ (2) 求直线AC1与平面ABB1所成的角的正弦值 17‎ 1. ‎(15分)已知等比数列{an}的公比q>1，且a3+a4+a5=28，a4+2是a3，a5的等差中项，数列{bn}满足b1=1，数列{(bn+1−bn)an}的前n项和为2n2+n (1) 求q的值 (2) 求数列{bn}的通项公式 17‎ 17‎ 1. ‎(15分)如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上 (1) 设AB中点为M，证明：PM垂直于y轴 (2) 若P是半椭圆x2+‎ ‎y‎2‎‎4‎=1(x<0)上的动点，求△PAB面积的取值范围 2. ‎(15分)已知函数f(x)=x−lnx (1) 若f(x)在x=x1，x2(x1≠x2)处导数相等，证明：f(x1)+f(x2)>8−8ln2‎ (2) 若a≤3−4ln2，证明：对于任意k>0，直线y=kx+a与曲线y=f(x)有唯一公共点 17‎ 17‎ 17‎ 17‎ 17‎ 17‎ 17‎ 17‎ 17‎ 17‎ 17‎