高考数学精练6不等式复习教案新人教版 14页

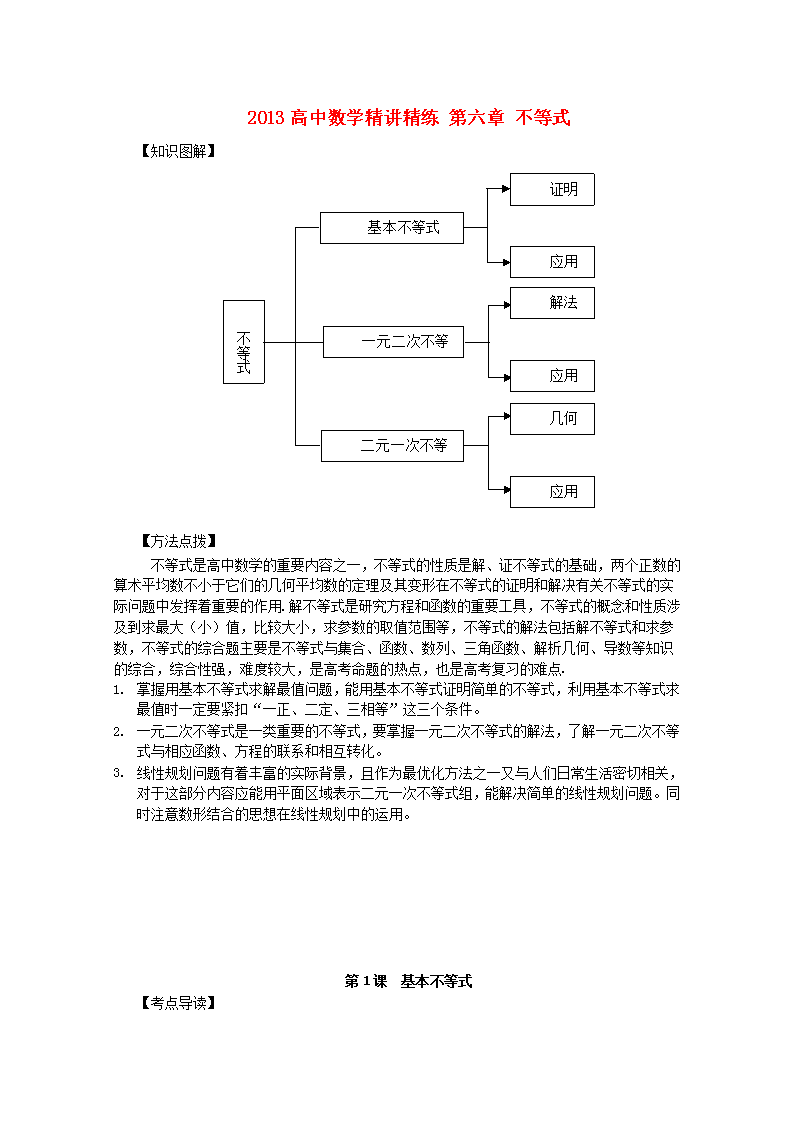
‎2013高中数学精讲精练 第六章 不等式 ‎【知识图解】‎ 不等式 一元二次不等式 基本不等式 二元一次不等式组 应用 解法 应用 几何意义 应用 证明 ‎ ‎ ‎ ‎ ‎【方法点拨】‎ 不等式是高中数学的重要内容之一，不等式的性质是解、证不等式的基础，两个正数的算术平均数不小于它们的几何平均数的定理及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的作用.解不等式是研究方程和函数的重要工具，不等式的概念和性质涉及到求最大（小）值，比较大小，求参数的取值范围等，不等式的解法包括解不等式和求参数，不等式的综合题主要是不等式与集合、函数、数列、三角函数、解析几何、导数等知识的综合，综合性强，难度较大，是高考命题的热点，也是高考复习的难点.‎ 1. 掌握用基本不等式求解最值问题，能用基本不等式证明简单的不等式，利用基本不等式求最值时一定要紧扣“一正、二定、三相等”这三个条件。‎ 2. 一元二次不等式是一类重要的不等式，要掌握一元二次不等式的解法，了解一元二次不等式与相应函数、方程的联系和相互转化。‎ 3. 线性规划问题有着丰富的实际背景，且作为最优化方法之一又与人们日常生活密切相关，对于这部分内容应能用平面区域表示二元一次不等式组，能解决简单的线性规划问题。同时注意数形结合的思想在线性规划中的运用。‎ 第1课　基本不等式 ‎【考点导读】‎ 1. 能用基本不等式证明其他的不等式，能用基本不等式求解简单的最值问题。‎ 2. 能用基本不等式解决综合形较强的问题。‎ ‎【基础练习】‎ ‎1.“a>b>‎0”‎是“ab<”的充分而不必要条件(填写充分而不必要条件、必要而不充分条件、充分必要条件、既不充分也不必要条件)‎ ‎2.的最小值为 ‎3.已知，且，则的最大值为 ‎4.已知，则的最小值是2‎ ‎【范例导析】‎ 例1.已知，求函数的最大值.‎ 分析：由于，所以首先要调整符号.‎ 解：∵∴‎ ‎∴y=4x-2+=≤-2+3=1‎ 当且仅当，即x=1时，上式成立，故当x=1时，.‎ 例2.（1）已知a，b为正常数，x、y为正实数，且，求x+y的最小值。‎ ‎（2） 已知，且，求的最大值．‎ 分析：问题（1）可以采用常数代换的方法也可以进行变量代换从而转化为一元函数再利用基本不等式求解；问题（2）既可以直接利用基本不等式将题目中的等式转化为关于的不等式，也可以采用变量代换转换为一元函数再求解.‎ 解:(1)法一：直接利用基本不等式：≥当且仅当，即时等号成立 法二：‎ 由得 ‎ ‎ ‎∵ x>0，y>0，a>0 ∴ 由>0得y-b>0 ∴ x+y≥‎ 当且仅当，即时，等号成立 ‎（2）法一：由，可得，．‎ ‎ ‎ 注意到．可得，．‎ 当且仅当，即时等号成立，代入中得，故的最大值为18．‎ 法二：，，‎ 代入中得：‎ 解此不等式得．下面解法见解法一，下略．‎ 点拨：求条件最值的问题，基本思想是借助条件化二元函数为一元函数，代入法是最基本的方法，也可考虑通过变形直接利用基本不等式解决. ‎ ‎【反馈练习】‎ ‎1.设a＞1,且,则的大小关系为m＞p＞n ‎ ‎2.已知下列四个结论：‎ ‎①若则； ②若,则；‎ ‎③若则； ④若则。‎ 其中正确的是④‎ ‎3.已知不等式对任意正实数恒成立，则正实数的最小值为6‎ ‎4.（1）已知：，且：，求证：，并且求等号成立的条件．‎ ‎（2）设实数x，y满足y+x2=0，00的解集是 ‎4.若不等式的解集是，则b=__-2____ c=__-3____.‎ ‎【范例导析】‎ 例.解关于ｘ的不等式 分析：本题可以转化为含参的一元二次不等式，要注意分类讨论.‎ 解:原不等式等价于∵∴等价于：‎ ‎ （*）‎ a>１时，（*）式等价于>0∵<１∴x<或x>２‎ a<１时，（*）式等价于<0由２－＝知：‎ 当0２，∴２１时，原不等式的解集为（－∞，）∪（2，＋∞）。‎ 思维点拨:含参数不等式,应选择恰当的讨论标准对所含字母分类讨论,要做到不重不漏.‎ ‎【反馈练习】‎ ‎1.若关于x的不等式的解集为R，则的取值范围是 ‎ ‎2.不等式解集为，则ab值分别为-12，-2‎ ‎3.若函数f(x) = 的定义域为R，则的取值范围为 ‎4.已知M是关于x的不等式2x2+(‎3a－7)x+3＋a－‎2a2<0解集，且M中的一个元素是0，求实数a的取值范围，并用a表示出该不等式的解集.‎ 解：原不等式即(2x－a－1)(x＋‎2a－3)<0，‎ 由适合不等式故得，所以，或.‎ 若，则，∴，‎ 此时不等式的解集是；‎ 若，由，∴，‎ 此时不等式的解集是。‎ 第3课　线性规划 ‎【考点导读】‎ 1. 会在直角坐标系中表示二元一次不等式、二元一次不等式组对应的区域，能由给定的平面区域确定所对应的二元一次不等式、二元一次不等式组.‎ 2. 能利用图解法解决简单的线性规划问题，并从中体会线性规划所体现的用几何图形研究代数问题的思想.‎ ‎【基础练习】‎ ‎1.原点（0,0）和点P（1,1）在直线的两侧，则a的取值范围是00，x－y+2>0，2x+y－5<0‎ 因此所求区域的不等式组为 x+2y－1≥0，x－y+2≥0，2x+y－5≤0‎ 作平行于直线3x－2y=0的直线系3x－2y=t（t为参数），即平移直线y=x，观察图形可知：当直线y=x－t过A（3，－1）时，纵截距－t最小此时t最大，tmax=3×3－2×（－1）=11；当直线y=x－t经过点B（－1，1）时，纵截距－t最大，此时t有最小值为tmin= 3×（－1）－2×1=－5‎ 因此，函数z=3x－2y在约束条件x+2y－1≥0，x－y+2≥0，2x+y－5≤0下的最大值为11，最小值为－5‎ ‎。‎ 第4课　不等式综合 ‎【考点导读】‎ 能利用不等式性质、定理、不等式解法及证明解决有关数学问题和实际问题，如最值问题、恒成立问题、最优化问题等.‎ ‎【基础练习】‎ ‎1.若函数，则与的大小关系是 ‎2.函数在区间上恒为正，则的取值范围是0＜a＜2‎ ‎3.当点在直线上移动时，的最小值是7‎ ‎4.对于0≤m≤4的m，不等式x2+mx＞4x+m－3恒成立，则x的取值范围是x＞3或x＜－1‎ ‎【范例导析】‎ 例1、已知集合，函数的定义域为Q ‎（1）若，求实数a的取值范围。‎ ‎（2）若方程在内有解，求实数a的取值范围。‎ 分析：问题（1）可转化为在内有有解；从而和问题（2）是同一类型的问题，既可以直接构造函数角度分析，亦可以采用分离参数.‎ 解：（1）若，在内有有解 ‎ 令 当时，‎ 所以a>-4,所以a的取值范围是 ‎（2）方程在内有解， 则在内有解。‎ ‎ ‎ 当时，‎ 所以时，在内有解 点拨：本题用的是参数分离的思想.‎ 例2.甲、乙两地相距，汽车从甲地匀速行驶到乙地，速度不超过，已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度的平方成正比，且比例系数为；固定部分为元．‎ ‎（1）把全程运输成本元表示为速度的函数，并指出这个函数的定义域；‎ ‎（2）为了使全程运输成本最小，汽车应以多大速度行驶？‎ 分析：需由实际问题构造函数模型，转化为函数问题求解 解：（1）依题意知汽车从甲地匀速行驶到乙地所用的时间为，全程运输成本为 ‎．故所求函数为，定义域为．‎ ‎（2）由于都为正数，‎ 故有，即．‎ 当且仅当，即时上式中等号成立．‎ 若时，则时，全程运输成本最小；‎ 当，易证，函数单调递减，即时，．‎ 综上可知，为使全程运输成本最小，‎ 在时，行驶速度应为；‎ 在时，行驶速度应为．‎ 点拨：本题主要考查建立函数关系式、不等式性质（公式）的应用．也是综合应用数学知识、思想和方法解决实际问题的一道优秀试题．‎ ‎【反馈练习】‎ ‎1.设，函数，则使的的取值范围是 ‎2.如果函数的单调递增区间是(-∞，a]，那么实数a的取值范围是____ a<-1____‎ ‎3.若关于的不等式对任意恒成立，则实数的取值范围为 ‎4已知二次函数f (x)=,设方程f (x)=x的两个实根为x1和x2．如果x1<2＜x2<4，且函数f (x)的对称轴为x=x0，求证：x0＞—1．‎ 证明：设g(x)= f (x)—x=，且g(4)>0，即 ‎∴‎