2015上海市各区高考物理二模分类汇编专题十磁场 电磁感应 22页

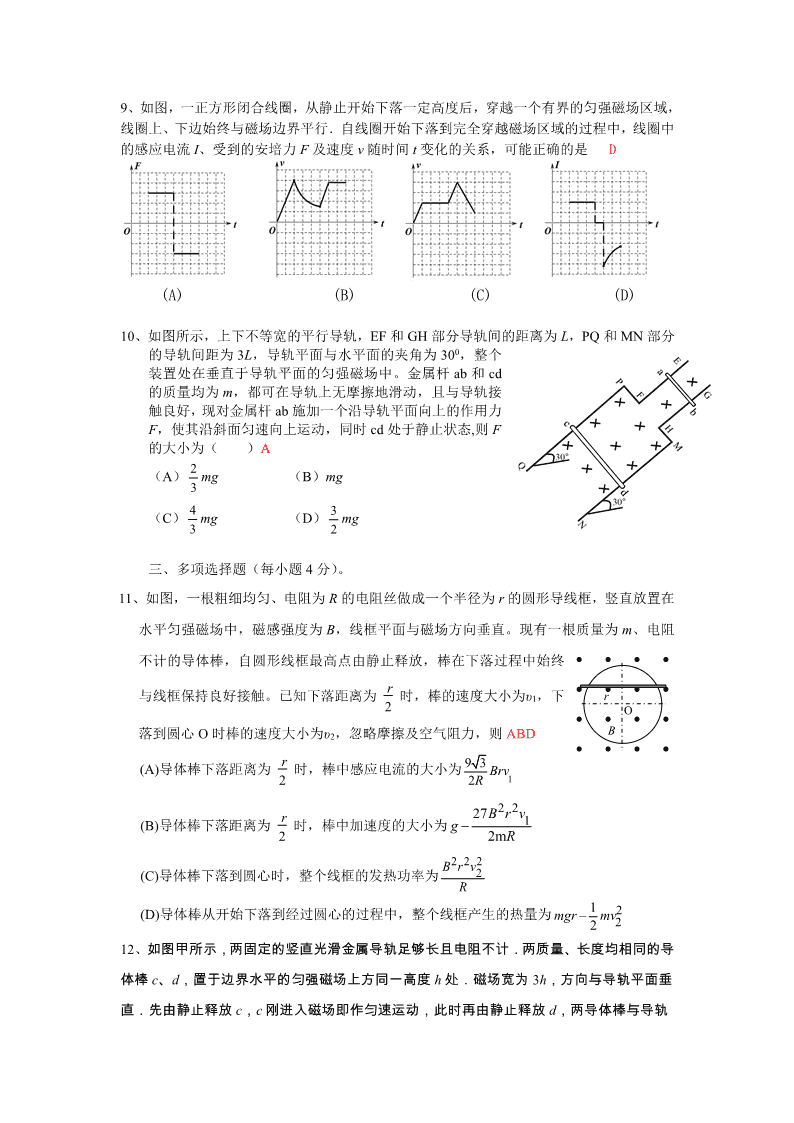
专题十、磁场 电磁感应（B 卷） 一、单项选择题（每小题 2 分）。 1、如图所示，两个闭合正方形线框 A、B 的中心重合，放在同一水平面内。当小线框 A 中 通有不断增大的顺时针方向的电流时，对于线框 B，下列说法中正确的是（ ）D （A）有顺时针方向的电流且有收缩的趋势 （B）有顺时针方向的电流且有扩张的趋势 （C）有逆时针方向的电流且有收缩的趋势 （D）有逆时针方向的电流且有扩张的趋势 二、单项选择题（每小题 3 分） 2、如图(甲)，闭合铜环由高处从静止开始下落，穿过一根竖直悬挂的条形磁 铁，铜环的中心轴线与条形磁铁的中轴线始终保持重合。若取磁铁中心 O 为 坐标原点，建立竖直向下为正方向的 x 轴，则图(乙)中最能正确反映环中感应 电流 i 随环心位置坐标 x 变化的关系图像是 答案：B 3、如图所示，一圆形闭合小铜环从高处由静止开始下落，穿过一根竖直悬挂的、质量为 m 的条形磁铁，铜环的中心轴线与条形磁铁的中心轴线始终保持重合。则细绳中弹力 F 随时 间 t 的变化关系图像可能是 （ ） B 4、如图所示，两同心圆环 A、B 置于同一光滑水平桌面上，其中 A 为均匀带电绝缘环，B 为导体环，若 A 环以图示的顺时针方向转动，且转速逐渐增大，则 C (A) B 环将顺时针转动起来 (B) B 环对桌面的压力将增大 (C) B 环将有沿半径方向扩张的趋势 (D) B 环中有顺时针方向的电流 N S t0 mg F （A） （B） （C） （D） t0 mg F t0 mg F t0 mg F B A ω M N S p a b 5、 两根相距为 L 的足够长的金属直角导轨如图所示放置，它们各有一部分在同一水平面内， 另一部分垂直于水平面。质量均为 m 的金属细杆 ab、cd 与导轨垂直 接触形成闭合回路，杆与导轨之间的动摩擦因数均为 μ，导轨电阻不 计，回路总电阻为 2R。整个装置处于磁感应强度大小为 B，方向竖直向 上的匀强磁场中．当 ab 杆在平行于水平导轨的拉力 F 作用下以速度 v1 沿导轨匀速运动时，cd 杆也正好以速度 v2 向下匀速运动．重力加 速度为 g．下列说法中正确的是 D （A）ab 杆所受拉力 F 的大小为 （B） cd 杆所受摩擦力为零 （C）回路中的电流强度为 （D） μ 与 v1 大小的关系为 6、如图所示，条形磁铁放在光滑水平桌面上，在其中央正上方固定一根长直导线，导线与 磁铁垂直．现给导线通以垂直于纸面向里的电流，则与通电前相比，导线通电后磁铁 （ ）． A．对桌面的压力增大，向左移动 B．对桌面的压力增大，不动 C．对桌面的压力减小，向右移动 D．对桌面的压力减小，不动 B 7、如图所示，两个相同的闭合铝环 M、N 套在一根光滑的绝 缘水平杆上，螺线管的轴线与铝环的圆心在同一直线上， 闭合电键 S 后，向左快速移动滑动变阻器的滑片 p，不考 虑 两 环 间 的 相 互 作 用 力 ， 则 在 移 动 滑 片 p 的 过 程 中 （C ）． A．M、N 环向左运动，它们之间的距离增大 B．M、N 环向左运动，它们之间的距离减小 C．M、N 环向右运动，它们之间的距离增大 D．M、N 环向右运动，它们之间的距离减小 8、如图，一圆形闭合铜环由高处从静止开始下落，穿过一根质量为 m、竖直悬挂的条形磁 铁，细绳对磁铁的拉力为 F。若线圈下落过程中，铜环的中心轴线与条形磁铁的中轴始 终保持重合，则下列图中能正确描述拉力 F 随时间 t 变化的图像是 B R vLB 2 1 22 R vvBL 2 )( 21 + 1 22 2 vLB Rmg=µ F y/ c m t y/ c m mg O F y/ c m t y/ c m mg O F y/ c m t y/ c m mg O （A） （B） （C） （D） F y/ c m t y/ c m mg O × NS II N S 9、如图，一正方形闭合线圈，从静止开始下落一定高度后，穿越一个有界的匀强磁场区域， 线圈上、下边始终与磁场边界平行．自线圈开始下落到完全穿越磁场区域的过程中，线圈中 的感应电流 I、受到的安培力 F 及速度 v 随时间 t 变化的关系，可能正确的是 D (A) (B) (C) (D) 10、如图所示，上下不等宽的平行导轨，EF 和 GH 部分导轨间的距离为 L，PQ 和 MN 部分 的导轨间距为 3L，导轨平面与水平面的夹角为 300，整个装 置处在垂直于导轨平面的匀强磁场中。金属杆 ab 和 cd 的质 量均为 m，都可在导轨上无摩擦地滑动，且与导轨接触良好， 现对金属杆 ab 施加一个沿导轨平面向上的作用力 F，使其 沿斜面匀速向上运动，同时 cd 处于静止状态,则 F 的大小为 （ ）A （A） mg （B）mg （C） mg （D） mg 三、多项选择题（每小题 4 分）。 11、如图，一根粗细均匀、电阻为 R 的电阻丝做成一个半径为 r 的圆形导线框，竖直放置在 水平匀强磁场中，磁感强度为 B，线框平面与磁场方向垂直。现有一根质量为 m、电阻 不计的导体棒，自圆形线框最高点由静止释放，棒在下落过程中始终 与线框保持良好接触。已知下落距离为 r 2时，棒的速度大小为 υ1，下 落到圆心 O 时棒的速度大小为 υ2，忽略摩擦及空气阻力，则 ABD (A)导体棒下落距离为 r 2时，棒中感应电流的大小为 (B)导体棒下落距离为 r 2时，棒中加速度的大小为 (C)导体棒下落到圆心时，整个线框的发热功率为 (D)导体棒从开始下落到经过圆心的过程中，整个线框产生的热量为 12、如图甲所示，两固定的竖直光滑金属导轨足够长且电阻不计．两质量、长度均相同的导 体棒 c、d，置于边界水平的匀强磁场上方同一高度 h 处．磁场宽为 3h，方向与导轨平面垂 直．先由静止释放 c，c 刚进入磁场即作匀速运动，此时再由静止释放 d，两导体棒与导轨 3 2 3 4 2 3 1 9 3 2 BrvR 2 2 127 2m B r v g R − 2 2 2 2B r v R 2 2 1 2mgr mv− O B r 始终保持良好接触．用 ac 表示 c 的加速度，Ekd 表示 d 的动能，xc、xd 分别表示 c、d 相对释 放点的位移．图乙中正确的是 BD 13、如图所示，由一根绝缘导线绕成半径相同的两个小圆（中央缺口很小）组成的线圈水平 放置，匀强磁场 B 垂直通过线圈平面，若将磁场的磁感强度从 B 增大到 2B 的过程中通过线 圈的电量为 Q，则下列可使线圈中通过电量为 Q 的过程是 （A）保持磁场Ｂ不变，将线圈平面翻转 90° （B）保持磁场Ｂ不变，将线圈平面翻转 180° （C）保持磁场Ｂ不变，将线圈的一个小圆平面翻转 180° （D）保持磁场Ｂ不变，将线圈拉成一个大圆 答案：ACD 14、如图（甲）所示，相距为 2L 的光滑平行金属导轨水平放置，右侧接有定值电阻 R，导 轨电阻忽略不计，OO′的左侧存在垂直于导轨平面向下、磁感应强度为 B 的匀强磁场。在 OO′ 左侧 L 处垂直导轨放置一质量为 m、电阻为 0.5R 的金属杆 ab，ab 在恒力 F 的作用下由静止 开始向右运动 3L 的距离，其速度与位移的变化关系如图（乙）所示。下列判断中正确的是 （ ） （A）ab 即将离开磁场时，安培力的大小为 （B）整个运动的过程中，通过电阻 R 上的电量为 2 2 12 3 B L R v 24 3 BL R 图乙A B C D ac xcO o h 2h 3h 4h 5h ac xcO o h 2h 3h 4h 5h Ekd xdO o h 2h 3h 4h 5h Ekd xdO o h 2h 3h 4h 5h c、d h 3h 图甲 3L0 v/m·s-1 v2 v1 L x/m 图（乙） b a O O′ B R L 图（甲） 2L （C）ab 即将离开磁场时，加速度的大小为 （D）整个过程中，电阻 R 上产生的焦耳热为 BCD 15、如图甲为磁感强度 B 随时间 t 的变化规律，磁场方向垂直纸面，规定向里的方向为正。 在磁场中有一平面位于纸面内的细金属圆环，如图乙所示。令 I1、I2、I3 分别表示 Oa、ab、 bc 段的感应电流，F1、F2、F3 分别表示金属环 上很小一段导体受到的安培力。下列说法正确 的是 （ ABD ） （A）I1 沿逆时针方向，I2 沿顺时针方向 （B）I2 沿顺时针方向，I3 沿顺时针方向 （C）F1 方向指向圆心，F2 方向指向圆心 （D）F2 方向背离圆心向外，F3 方向指向圆 心 16、在倾角为 θ 的斜面上固定两根足够长且间距为 L 的光滑平行金属导轨 PQ、MN，导轨 处于磁感应强度为 B 的匀强磁场中，磁场方向垂直于斜面向下．有两根质量分别为 m1 和 m2 的金属棒 a、b，先将 a 棒垂直于导轨放置，用跨 过光滑定滑轮的细线与物块 c 连接，连接 a 棒的细线平 行于导轨，由静止释放 c，此后某时刻，将 b 也垂直于 导轨放置，此刻起 a、c 做匀速运动而 b 静止，a 棒在运 动过程中始终与导轨垂直，两棒与导轨电接触良好， 导轨电阻不计，则（ ）． A．物块 c 的质量是（m1+m2）sinθ B．b 棒放上导轨前，物块 c 减少的重力势能等于 a、c 增加的动能 C．b 棒放上导轨后，a 棒克服安培力所做的功等于 a 棒上消耗的电能 D．b 棒放上导轨后，b 棒中电流大小是 AD 17、如图所示，有一不计内阻、可调电压的电源 E 与可调电阻 R、电 键 K 组成正方形电路，正中心有一圆形小导线圈 A．闭合电键 K，待稳 定，若要使小导线圈 A 中产生恒定的感应电流，则只在改变一个物理 量的情况下，以下表示 E、R 随时间 t 变化的图像中成立的是（已知离 通电细直导线一定距离处的磁感应强度大小与电流强度大小成正比）AD 2 2 2 2 2 1 1- 8 4 3 B L L mR −v v v 2 2 2 1 1 36 m( − )v v 2 sinm g BL θ 18、如图，两同心圆环 A、B 置于同一水平面上，其中 B 为均匀带负电绝缘环，A 为导体环。 当 B 绕轴心顺时针转动且转速增大。下列说法正确的是 ( BD ) A．A 中产生逆时针的感应电流 B．A 中产生顺时针的感应电流 C．A 具有收缩的趋势 D．A 具有扩展的趋势 四、填空题。 19、匀强磁场中有一半径为 0.2m 的圆形闭合线圈，线圈平面与磁场垂 直。已知线圈共 50 匝，其阻值为 2Ω。匀强磁场磁感应强度 B 在 0∼1s 内从零均匀变化到 0.2 T，在 1∼5 s 内从 0.2 T 均匀变化到 -0.2 T。 则 0.5s 时该线圈内感应电动势的大小 E＝_________V；在 1∼5s 内 通过线圈的电荷量 q＝_________C。 1.256 1.256 20、如图所示，导线全部为裸导线，半径为 r 的圆内有垂直于平面 的匀强磁场，磁感应强度为 B，一根长度大于 2r 的导线 MN 以速度 v 在圆环上无摩擦地自左向右匀速滑动，电路的固定电阻为 R，其 余电阻忽略不计．在 MN 滑动过程中，通过电阻 R 上的电流的平 均值为　　　　　，当 MN 从圆外的左端滑到右端时，通过 R 的电荷量为　　　　　． 24、 Bπrv/2R，Bπr2/R 21、光滑金属导轨宽 L＝0.4m，电阻不计，均匀变化的磁 场穿过整个轨道平面，如图甲所示。磁场的磁感应强度随 时间变化的情况如图乙所示。金属棒 ab 的电阻为 1Ω， 自 t＝0 时刻起从导轨最左端以 v0＝1m/s 的速度向右匀 速运动，则 1 秒末回路中的电动势为 1.6v v，此时 ab 棒 所受磁场力为 1.28N N。 22、如图所示，在水平面上有两条长度均为 4L、 间距为 L 的平行直轨道，处于竖直向下的匀强 磁场中，磁感应强度为 B．横置于轨道上长为 L 的滑杆向右运动，轨道与滑杆单位长度的电阻均 为 ，两者无摩擦且接触良好．轨道两侧分别 连接理想电压表和电流表．若将滑杆从轨道最左侧匀速移动到最右侧，当滑竿到达轨道正中 间时电压表示数为 U，则滑竿匀速移动的速度为_____ _______，在滑动过程中两电表读 L R 5 4 U BL B R B M N × × × ×× × × 4L L B Aω 数的乘积的最大值为_______ __________. 23、轻质细线吊着一质量 m＝0.8kg，边长 L＝0.8m、匝 数 n＝20、总电阻 r＝1Ω 的正方形线圈。边长 l=0.4m 的 正方形磁场区域对称地分布在线圈下边的两侧，磁场方 向垂直纸面向里，如图甲所示，磁感应强度 B 随时间变 化规律如图乙所示。从 t＝0 开始经 t0 时间细线开始松弛， 在前 t0 时间内线圈中产生的感应电流为 A，t0 的 值为 s。 0.8；0.5 24、如图（a）所示，边长为 1m、电阻为 0.1Ω 的正方形金属框 abcd 水平放置，e、f 分别为 bc、 ad 的中点。某时刻起在 abef 区域内有竖直向下 的磁场，其磁感应强度 B1 的大小随时间变化的 规律如图（b）所示，ab 边恰在磁场边缘以外；fecd 区域内有竖直向上的匀强磁场，磁感应强度 B2＝ 0.5T，cd 边恰在磁场边缘以内，两磁场均有理想 边界。则 dc 边中流过的感应电流方向为________（选填“d→c”或“c→d”，金属框受到的 安培力大小为________N。（取 g＝10m/s2）c→d，2.5 25、如图（1），正三角形金属线框水平放置，总电阻为 1Ω，边长为 3m，处在两个半径均为 1m 的圆形匀强磁场区域中。线框顶点与右侧圆中心重合，线框底边中点与左侧圆中心重合。 磁感应强度 B1 垂直水平面向外，大小不变，B2 垂直水平面向里，大小随时间变化，B1、B2 的值如图（2）。则 t=0.6s 时穿过线框的磁通量为_______Wb，t=0.3s 时线框整体受到的安培 力为_______N。（取π≈3）1，13.75 五、计算题． 26、 (14 分) 如图 a 所示，间距为 L 的光滑平行长导轨固定在水平面上，每根导轨单位长度 电阻为 R0。导轨间存在竖直方向的有界匀强磁场。不计电阻的金属杆①、②垂直导轨放 225 64 U R （b） )) 1 1 B1/T O t/s （a） d b B1 B2 c a e f （1） B1 B2 2 （2） 2 0 t/s 0.2 0.4 0.6 B/T B2 B1 －1 5 置在磁场内，杆①在离开磁场边界左侧 2L 处，杆②在杆①右侧。磁感应强度变化规律满 足 B=B0－kt (B0、k 为已知量)。 (1) 若杆①和杆②都固定，求杆中的感应电流强度。 (2) 若杆①和杆②以相同速度 υ 向右匀速运动，在杆②出磁场前，求杆中的感应电流强度。 (3) 若杆①固定，t=0 时，杆②从杆①右侧 L 处出发向右运动的过程中，保持闭合回路中 磁通量不变使杆中一直无感应电流，则杆②多久后到达磁场边界？ (4) 若磁感应强度保持 B=B0 不变，杆①固定。杆②以一定初速度、在水平拉力作用下从 杆①右侧 0.5m 处出发向右运动，速度 υ 与两杆间距 x 之间关系满足图 b。当外力做功 4.5J 时，两杆间距 x 为多少？（第 4 问中可用数据如下：B0=1T、R0=0.1Ω/m、L=0.5m、 金属杆②质量 m=0.5kg） 33.(14 分） （1）设杆①和杆②间距 x ……3 分 （2）因为两杆的运动不影响磁通量大小，所以感应电流与静止时相同，即与（1）问中 相同。 ……3 分 （3）磁通量保持不变，杆①和杆②间距 x 的任意位置有 当 x=2L 时 ……3 分 （4）根据 v-x 图像可知，v=2x 感应电流 =5A，为定值 则安培力 FA=ILB0=2.5N……2 分 由动能定理，仅水平拉力和安培力做功，设杆①和杆②间距 x W+WA=ΔEk 0000 2222 R kL xR kLx xR t xR EI ==∆ ∆ == ϕ 02R kLI = LxktBLB )( 0 2 0 −= k Bt 2 0= xR LvB xR EI 0 0 0 22 == 2 0 2 2 1 2 1)( mvmvLxFW tA −=−− 0 0.5 1.0 x/m 1 υ/m·s-1 图 b L 2L B 杆① 杆② 图 a 4.5-2.5(x-0.5)=x2-0.25 得 x=1.5m……2 分 由题意，安培力仅存在于金属杆未出磁场区域，根据 x=1.5m 可知金属杆已出磁场 （学生可能判断金属杆刚到磁场边界时，外力做功小于 4.5J） 由动能定理 4.5-1.25= x2-0.25 x=1.87m……1 分 27、（14 分）如图所示，两根足够长的光滑直金属导轨 MN、PQ 平行固定在倾角 的 绝缘斜面上，两导轨间距 m，导轨的电阻可忽略。 、 两点间接有阻值为 的电 阻．一根质量 kg、电阻 的均匀直金属杆 放在两导轨上，与导轨垂直且接触 良好． 整套装置处于磁感应强度 T 的匀强磁场中，磁场方向垂直斜面向下．自图示位 置起，杆 受到大小为 （式中 为杆 运动的速度，力 的单位为 N）、 方向平行导轨沿斜面向下的拉力作用，由静止开始运动，测得通过电阻 的电流随时间 均匀增大． 取 10m/s2， ． （1）试判断金属杆 在匀强磁场中做何种运动，并请写出推理过程； （2）求电阻 的阻值； （3）已知金属杆 自静止开始下滑 m 的过程中，电阻 上产生的焦耳热 为 J， 求该过程需要的时间 和拉力 做的功 ． 33、（14 分）解： ⑴ 金属杆做匀加速运动（或金属杆做初速为零的匀加速运动）。 （1 分） 通过 R 的电流 ，因通过 R 的电流 随时间均匀增大，即杆的速度 随时 间均匀增大，杆的加速度为恒量，故金属杆做匀加速运动。 （2 分） 2 0 2 2 1 2 1 mvmvLFW tA −=− 37θ = ° 1L = M P R 1m = 0.2r = Ω ab 0.5B = ab 0.5 2F v= + v ab F R g sin37 0.6° = ab R ab 1x = R R 1 0.8Q = t F W rR BLv rR EI +=+= I v ⑵ 对回路，根据闭合电路欧姆定律 （1 分） 对杆，根据牛顿第二定律有： （1 分） 将 代入得： ， （2 分） 因 与 无关（取刚开始运动时刻，v=0），所以 ， 得 （2 分） ⑶ 由 得，所需时间 （1 分） 电路中总的焦耳热为： （2 分） 由能量守恒定律得： 解得: （2 分） 28、(14 分）如图所示，竖直平面内有足够长的光滑的两条竖直平行金属导轨，上端接有一 个定值电阻 R0，两导轨间的距离 L=2m，在虚线的区域内有与导轨平面垂直的匀强磁场，磁 感应强度 B=0.2T，虚线间的高度 h=1m。完全相同的金属棒 ab、cd 与导轨垂直放置，质量 均为 m＝0.1 kg，两棒间用 l=2m 长的绝缘轻杆连接。棒与导轨间接触良好，两棒电阻皆为 r=0.3Ω，导轨电阻不计，已知 R0=2r。现用一竖直方向的外力从图示位 置作用在 ab 棒上，使两棒以 v=5m/s 的速度向下匀速穿过磁场区域 （不计空气和摩擦阻力，重力加速度 g 取 10 m/s2）。求： （1）从 cd 棒进磁场到 ab 棒离开磁场的过程中通过 ab 棒的电流大小 和方向； （2）从 cd 棒刚进磁场到 ab 棒刚离开磁场的过程中拉力做的功； （3）若 cd 棒以上述速度刚进入磁场时，将外力撤去，经一段时间 cd 棒匀速出磁场，求在此过程中电阻 R0 上产生的热量。 答案：33.解：（1）（4 分）cd 在磁场中时，ab 棒的电流方向为 b 到 a E=BLv=0.2×2×5=2V (方向 1 分、大小 1 分） 当 ab 在磁场中时，ab 棒的电流方向为 a 到 b， (方向 1 分、大小 1 分） （2）（5 分）当 cd、ab 分别在磁场中时，回路产生的热量 ，即克服安培力做的功。(2 分） rR BLvI += maBILsinmgF =−+ θ 25.0 += vF mavrR LBmg =+−++ )5.0(sin2 22 θ a v 282 s/mm sinmga =+= θ 05.0 22 =+− rR LB Ω= 3.0R 2 2 1 atx = sa xt 5.02 == 1 0.5 40.80.3 3 R rQ Q J JR += = × = 21sin 2W mg Q mvθ+ = + 10 3W J= Ω=++=++= 5.02 2 0 0 rrr rrRRR RRR cd ab ab 总 A3 8 5.0 2 9.0 3.02 0 0 =×=+= 总R E RR RI ab ab A45.0 2 === 总R EIab J2.35 1 5.0 22222 222 1 =××==== v h R EtR EQQ总 根据动能定理，得到 ， (公式 2 分、答案 1 分） （3）（5 分）当撤去外力后 cd 棒匀速出磁场，此时对两棒，根据平衡条件 2mg=Fcd 安， (2 分） 根据动能定理，得到 (2 分） 所以 R0 上产生的热量为 (1 分） 29、（14 分）如图（甲）所示，磁感应强度为 B 的匀强磁场垂直于纸面，在纸面内固定一条 以 O 点为圆心、半径为 L 的圆弧形金属导轨，长也为 L 的导体棒 OA 绕 O 点以角速度 ω 匀 速转动，棒的 A 端与导轨接触良好，OA、导轨、电阻 R 构成闭合电路。 （1）试根据法拉第电磁感应定律 ，证明导体棒产生的感应电动势 。 （2）某同学设计了一种带有闪烁灯的自行车后轮，如图（乙）所示。车轮与轮轴之间均匀 地连接 4 根金属条，每根金属条中间都串接一个小灯，阻值为 R=0.3Ω 并保持不变，车轮半 径 r1=0.4m，轮轴半径可以忽略。车架上固定一个强磁铁，可形成圆心角为 θ=60°的扇形匀 强磁场区域，磁感应强度 B=2.0T，方向如图（乙）所示。若自行车前进时，后轮顺时针转 动的角速度恒为 ω=10rad/s，不计其它电阻和车轮厚度。求金属条 ab 进入磁场时，ab 中感 应电流的大小和方向。 （3）上问中，已知自行车牙盘半径 r2=12cm，飞轮半径 r3=6cm，如图（丙）所示。若该同 学骑车时每分钟踩踏脚板 60 圈，车辆和人受到外界阻力的大小恒为 10N，他骑车 10 分钟的 时间内一共需要对自行车做多少功？ 0)2 =−++ 克安（ WhlmgWF J8.22.3)21101.02-)2- −=++××=++= （（ 克安WhlmgWF 总R vLBmg 2 22 2 = m/s25.622.0 5.0101.022 22222 =× ×××== LB mgRv 总 22 2 22 122 12 mvmvWmgh −=− 克安 J6.051.022 125.61.022 11101.0222 122 12 2222 2 =×××+×××−×××=+−= mvmvmghW克安 rtItRIQW 3 522 总总总总克安 === J08.015 2 5 3 9 229 1)3 1( 2 0 2 ===== 克安总总总 WQrtItRIQ E n t φ∆= ∆ 21 2E B Lω= B O R L ωA 图（甲） r1 B a b v ω 图（乙） 车轮 轮轴 飞轮 后轮 牙盘 踏脚 图（丙） 33．（14 分）解答与评分标准： （1）设金属棒 OA 在 Δt 时间内扫过的面积为 ΔS，则： （1 分） 磁通改变量 （1 分） 根据法拉第电磁感应定律得到 （1 分） （2）根据右手定则知：ab 中的电流方向为 b→a （1 分） ab 相当于电源，电动势 =1.6V （2 分） 电路总电阻 =0.4Ω （1 分） 通过 ab 中的电流： =4A （1 分） （3）后轮转速 n=2r/s，后轮角速度 ω=4π rad/s， （1 分） 车速 v=r1ω=1.6πm/s （1 分） 电动势 =0.64π V ，总的电功率 P 总= = W （1 分） 总的焦耳热 Q=P 总( t)= 409.6π2=4.04×103J （1 分） 克服阻力做功 =3.016×104J （1 分） 一共需要做功 W 总=Wf+ Q =3.42×104J （1 分） 30、 （14 分）如图所示，一对光滑的平行金属导轨固定在同一水平面内，导轨间距 l＝ 0.5m，左端接有阻值 R＝0.3Ω 的电阻，一质量 m＝0.1kg，电阻 r＝0.1Ω 的金属棒 MN 放置 在导轨上，整个装置置于竖直向上的匀强磁场中，磁场的磁感应强度 B＝0.4T．棒在水平向 右的外力作用下，由静止开始以加速度 a＝2m/s2 做匀加速运动，当棒的位移 x＝9m 时撤去 外力，棒继续运动一段距离后停下来，已知撤去外力前后回路中产生的焦耳热之比 Q1：Q2＝ 2：1．导轨足够长且电阻不计，棒在运动过程中始终与导轨垂直且两端与导轨保持良好接 触．求： （1）棒在匀加速运动过程中，通过电阻 R 的电荷量 q； （2）撤去外力后回路中产生的焦耳热 Q2； （3）外力做的功 WF． 33、（14 分 = 5+5+4） 2 21 1 2 2S L L tθ ω∆ = ⋅ = ∆ 21 2B S B L tφ ω∆ = ⋅∆ = ⋅∆ 21 2E n B Lt φ ω∆= =∆ 2 21 1 2.0 10 0.42 2E B Lω= = × × × 4 3 3 R RR R= + =总 1.6 0.4 EI R = = 总 2 1 1 2E B rω= 总R E 2 2128 125 π 2 3 f f fW F s F t= ⋅ = ⋅v 解：（1）设棒匀加速运动的时间为 t， 则磁通量的变化量为： （1 分） 电路中产生的平均电动势为： （1 分） 电路中产生的平均电流为： （1 分） 通过电阻 R 的电量： （1 分） 联立以上各式得： （1 分） （2）撤去外力前棒做匀加速运动的末速度为 v 由 （1 分） 得 （1 分） 撤去外力后，棒做减速运动直到静止，此过程只有安培力做功。 由动能定理： WA2=0﹣ mv2 ． （1 分） 焦耳热 Q2 等于棒克服安培力做的功：Q2= ﹣WA2 （1 分） 解得：Q2= mv2=1.8J （1 分） （3）撤去外力前的焦耳热为：Q1=2Q2=3.6J （1 分） 且 Q1 =﹣WA1 （WA1 为撤去外力前，安培力做的功） 根据动能定理有：WF﹣Q1 = mv2﹣0 （2 分） 解得：WF = 5.4J （1 分） （直接用功能原理：WF = Q1+Q2=5.4J 同样给分） 31、(16 分)图(甲)是磁悬浮实验车与轨道示意图，图(乙)是固定在车底部金属框 abcd(车厢与 金属框绝缘)与轨道上运动磁场的示意图．水平地面上有两根很长的平行直导轨 PQ 和 MN， 导轨间有竖直(垂直纸面)方向等间距的匀强磁场 Bl 和 B2，二者方向相反．车底部金属框的 ad 边宽度与磁场间隔相等，当匀强磁场 Bl 和 B2 同时以恒定速度 v0 沿导轨方向向右运动时，金 属框会受到磁场力，带动实验车沿导轨运动。设金属框垂直导轨的 ab 边长 L=0.20m、总电 阻 R=l.6Ω，实验车与线框的总质量 m=2.0kg，磁场 Bl=B2= 1.0T，磁场运动速度 v0=10m/s。 已知悬浮状态下，实验车运动时受到恒定的阻力 f=0.20N，求： (1)设 t=0 时刻，实验车的速度为零，求金属框受到的磁场力的大小和方向； (2)求实验车的最大速率 vm； (3)实验车以最大速度做匀速运动时，为维持实验车运动，外界在单位时间内需提供的总能 量? Blx=∆Φ tE ∆Φ= rR EI += tIq = Cq 5.4= axv 22 = s/m6=v (4)假设两磁场由静止开始向右做匀加速运动来起动实验车，当两磁场运动的时间为 t=30s 时，实验车正在向右做匀加速直线运动，此时实验车的速度为 v=4m/s，求由两磁场开始运 动到实验车开始运动所需要的时间 t0。 33.（16 分） 解：（1）t=0 时刻实验车速度为零，线框相对于磁场的速度大小为 v0 线框中产生的感应电动势为 E=2BLv0 感应电流为 金属框受到的磁场力的大小为 F=2BIL （1 分） 联立得 （1 分） 根据楞次定律判断，磁场力方向水平向右． （1 分） （2）实验车最大速率为 vm 时相对磁场的切割速率为 v0-vm，则此时线框 所受的磁场力大小为 （2 分） 此时线框所受的磁场力与阻力平衡，得：F=f （2 分） (3) 克服阻力的功率为 P1 = fvm=1.6W （1 分） 当实验车以速度 v 匀速运动时金属框中感应电流 （1 分） 金属框中的热功率为 P2 = I2R=0.4W （1 分） 外界在单位时间内需提供的总能量为 E=（P1+P2）t=2J （1 分） (4) 根据题意分析可得，为实现实验车最终沿水平方向做匀加速直线运 动，其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同 EI R = 2 2 2 2 04 4 1.0 0.20 10 1.01.6 B L vF N NR × × ×= = = 2 2 04 ( )mB L v vF R −= 0 2 2 2 2 1.6 0.2(10 ) / 8.0 /4 4 1.0 0.2m Rfv v m s m sB L ×= − = − =× × 0.20 0.52 2 1.0 0.20 fI A ABL = = =× × 设加速度为 a，则 t 时刻金属线圈中的电动势 E=2BL(at-v) 金属框中感应电流 （1 分） 又因为安培力 （1 分） 所以对试验车，由牛顿第二定律得 得 a=0.6m/s2 （1 分） 设从磁场运动到实验车起动需要时间为 t0，则 t0 时刻金属线圈中的电动 势 E0=2BLat0 金属框中感应电流 又因为安培力 （1 分） 对实验车，由牛顿第二定律得 F0=f 得：t0= （1 分） 32、（14 分）如图，固定在水平桌面上的“∠”型平行导轨足够长，间距 L=1m，电阻不计。 倾斜导轨的倾角 θ=53º，并与 R=2Ω的定值电阻相连。整个导轨置于磁感应强度 B=5T、方 向垂直倾斜导轨平面向上的匀强磁场中。金属棒 ab、cd 的阻值为 R1=R2=2Ω，cd 棒质量 m=1kg。 ab 与导轨间摩擦不计，cd 与导轨间的动摩擦因数μ=0.3，设最大静摩擦力等于滑动摩擦力。 现让 ab 棒从导轨上某处由静止释放，当它滑至某一位置时，cd 棒恰好开始滑动。 （1）求此时通过 ab 棒的电流； （2）求导体棒 cd 消耗的热功率与 ab 棒克服安培力做功的功率之比； （3）若 ab 棒无论从多高的位置释放，cd 棒都不动，则 ab 棒质量应小于多少？ （4）假如 cd 棒与导轨间的动摩擦因数可以改变，则当动摩擦因数满足什么条件时，无 论 ab 棒质量多大、从多高位置释放，cd 棒始终不动？ 2 ( )BL at vI R −= 2 24 ( )2 B L at vF BIL R −= = 2 24 ( )B L at v f maR − − = 0 0 2BLatI R = 2 2 0 0 0 42 B L atF BI L R = = 2 2 04B L at fR = 10 3 s 解：（1）ab 棒沿斜面滑下切割磁感线产生的感应电流的方向是 b→a，通过 cd 棒的电流方 向如图 c→d。cd 棒刚要开始滑动时，其受力分析如图所 示。 由平衡条件得： 由摩擦力公式得： 联立以上三式，得 Icd=1.67A,Iab=2Icd=3.34A （4 分） （2）根据题意画出等效电路如图所示： 设 ，因为电阻 R 与 cd 棒并联，故电阻 R 上产生的热功率与 cd 棒产生的热功 率相等，即 又因为流经 ab 棒的电流为 2I，故 ab 棒产生的热功 率 整个回路产生的热功率 又因为回路中消耗的热功率源于 ab 棒克服安培力做功，所以导体棒 cd 消耗的热功率 与 ab 棒克服安培力做功的功率之比为 （4 分） （3）ab 棒在足够长的轨道下滑时，最大安培力只能等于自身重力的分力，有： cd 棒所受最大安培力应为 ，要使 cd 棒不能滑动，需： 由以上两式联立解得： （3 分） （4）ab 棒下滑时，cd 棒始终静止，有： f=0 cd Lcos53BI μN=f 0 cd Lsin53BImgN += II cd = RIPP cdR 2== RIPab 24= RIP 26= 6 1 6P P 2 2 AF cd == RI RI 0 abA gsin53mF = AF2 1    +≤ 0 A 0 A 53sinF2 1mgμos53F2 1 c kg08.2mab≤ I 区 II 区 2d 2d 2d d M N 2d 2d 2d 解得： 当 ab 棒质量无限大，在无限长轨道上最终一定匀速运动，安培力 FA 趋于无穷大，cd 棒所受安培力 FAˊ亦趋于无穷大，有： （3 分） 33、（14 分）如图所示，水平面上有一个高为 d 的木块，木块与水平面间的动摩擦因数为 μ=0.1．由均匀金属材料制成的边长为 2d、有一定电阻的正方形单匝线框，竖直固定在 木块上表面，它们的总质量为 m．在木块右侧有两处相邻的边长均为 2d 的正方形区域， 正方形底边离水平面高度为 2d．两区域各有一水平方向的匀强磁场穿过，其中一个方 向垂直于纸面向里，另一个方向垂直于纸面向外，区域Ⅱ中的磁感应强度为区域Ⅰ中的 3 倍．木块在水平外力作用下匀速通过这两个磁场区域．已知当线框右边 MN 刚进入Ⅰ 区时，外力大小恰好为 ，此时 M 点电势高于 N 点，M、N 两点电势差 UMN=U．试求： （1）区域Ⅰ中磁感应强度的方向怎样？ （2）线框右边 MN 在Ⅰ区运动过程中通过线框任一横截面的电量 q． （3）MN 刚到达Ⅱ区正中间时，拉力的大小 F． （4）MN 在Ⅱ区运动过程中拉力做的功 W． 解：（1）向外． （2 分） （2）设线框的总电阻为 R，磁场Ⅰ区的磁感强度为 B，线框右边 MN 在Ⅰ区运动过程中 有一半长度切割磁感线产生感应电动势，有 ， （1 分） 线框右边 MN 在Ⅰ区运动过程中，木块与线框受力平衡，有 得 （1 分） 通过线框任一横截面的电量 q 为 ，其中 （1 分） 联立以上各式，解得 （1 分） ( )0ˊ A 0ˊ A 53sinFmgμos53F +≤c 0 ˊ A 0 0ˊ A 0ˊ A 53sin F 53cos 53sinF 53cosFμ + = + ≥ mgmg 75.053sin 53cosμ 0 0 =≥ 0 3 20 F gm= BdvI R R ε= = 3 3 4 4U I R Bdv= ⋅ = A =0F F mgµ− − A 3 1= 0.120 20F BId mg mg mg= − = q It= 2dt v = 3 40 mgdq U = （3）MN 刚到达Ⅱ区正中间时，流过线框的电流为 （1 分） 线框左、右两条边均受到向左的安培力作用，总的安培力大小为 （1 分） 由于线框上边各有一半处在磁场Ⅰ区、Ⅱ区中，所以分别受到向上与向下的安培力 作用，此时木块受到的支持力 N 为 （1 分） 木块与线框组成的系统受力平衡，因此拉力 F 为 （1 分） （4）随着 MN 在磁场Ⅱ区的运动，木块受到的支持力 Nx 随发生的位移 x 而变化，有 （1 分） 由于 Nx 随位移 x 线性变化，因此 MN 在Ⅱ区运动过程中木块受到的平均支持力为 （1 分） 此过程中拉力做的功 W 为 （2 分） 34、（15 分）如图（a），水平地面上固定一倾角为 37°的斜面，一宽为 l＝0.43m 的有界匀强 磁场垂直与斜面向上，磁场边界与斜面底边平行。在斜面上由静止释放一正方形金属线 框 abcd，线框沿斜面下滑时，ab、cd 边始终与磁场边界保持平行。以地面为零势能面， 从线框开始运动到恰好完全进入磁场的过程中，线框的机械能 E 与位移 s 之间的关系如 图（b）所示，图中①、②均为直线段。已知线框的质量为 m＝0.1kg，电阻为 R＝0.06Ω。 （sin37°＝0.6，cos37°＝0.8，重力加速度 g 取 10m/s2）求： （1）线框与斜面间的动摩擦因数 μ； （2）ab 边刚进入磁场时，线框的速度 v1； （3）线框刚进入磁场到恰好完全进入磁场所用的时间 t； （4）线框穿越磁场的过程中，线框中产生的最大电功率 Pm； 解：（1）根据线段①，减少的机械能 （1 分） =0.144J（1 分），其中 s1=0.36m 解得 μ=0.5（1 分） （2）未进入磁场时，线框的加速度 m/s2（1 分） 3 4' 4Bdv Bdv BdvI IR R += = = 4'= ' 3 ' 16 5A AF BI d BI d F mg+ = = 73 ' ' 8 5AN mg BI d BI d mg F mg= + − = + = 4 7 47' 5 50 50AF F N mg mg mgµ= + = + = 3 ' '(2 ) 2 ' 4 'xN mg BI x BI d x mg BI d BI x= + − − = − + 4 ' 2 72 ' 2 '2 5 BI dN mg BI d mg BI d mg ⋅∴ = − + = + = 4 7 47' 2 2 2 25 50 25AW F d N d mg d mg d mgdµ= ⋅ + ⋅ = ⋅ + ⋅ = fWE 克=Δ 1 J)756.0900.0(=°37cos=Δ 11 －smgμE 2=°37cos°37sin= gμga － b (a) (b) 37° l B a b c d 0.900 0 0.756 0.666 0.36 E/J s/m ① ② m/s（1 分） （3）线框进入磁场的过程中，减小的机械能等于克服摩擦力和安培力所做的功（1 分）， 由图线②可知，此时机械能线性减小，说明安培力也为恒力，线框做匀速运动。（1 分） （1 分） s2 为线框的边长，解得 s2=0.15m（1 分） （1 分） （4）线框进入磁场后始终做匀加速直线运动，当 ab 边要离开磁场时，开始做减速运动， 此时线框受到的安培力最大，速度最大，线框内的电功率最大（1 分） 由 ，可求得 v2=1.6m/s（1 分） 在线框匀速进入磁场时，安培力 （1 分） 又因为 可求出 （1 分） 所以 线框内的最大电功率 （1 分） 35、如图，在光滑水平桌面存在一沿 x 方向均匀增大的有界稳恒磁 场，其方向与桌面垂直，变化率 k ＝0.5T/m ，x ＝0 处磁场的磁感应强 度 B0 ＝0.5T．lab=0.4m，lbc=1m，质量为 m=0.1kg、电阻为 R=0.2Ω 的 长方形线框在外力作用下，从 x=0 处以某一初速度向右运动，运动 过程中线框中的电流如图所示．求： （1）线框的初速度 v0． （2）线框 cd 边进入磁场前瞬间的速度 v1． （3）线框从 x=0 运动到 x=1m 过程中安培力做功的大小． （4）线框从 x＝0 运动到 x＝2m 过程中外力的平均功率． 解：(1)由图可知，线框中的电流恒定： （2 分） (2) （3 分） (3) （3 分） smvR lvBI /2, 0 00 == 2.1=2= 11 asv J09.0=)666.0756.0(=)+(=+=Δ 22 －sFFWWE ff 安克安克 s125.0=2.1 15.0== 1 2 v st )(2+= 2 2 1 2 2 slavv － N2.0=°37cos°37sin= mgμmgF －安 R vLBBILF 1 22 ==安 01.0=22 LB W43.0=3 28.1=== 222 2 m 2 R vLB RIP smVTkLBBR LVBI bc /1,1, 101 11 =⇒=+== JLFWNF NILBFNILBF BFB abBabB B 6.0,6.02 8.04.0 ,8.0,4.0 1100 ===+= ==== (4) （1 分） x=1 到 x=2m, （1 分） （1 分) （1 分） 线框全部进入磁场（即 cd 边进入磁场）瞬间，线框动能有突变。 （1 分） （1 分） 第（4）问解法 2： 36、（14 分）如图所示，质量为 m 的足够长的“［”金属导轨 abcd 放在倾角为 θ 的光滑绝 缘斜面上，bc 段电阻为 R，其余段电阻不计。另一电阻为 R、质量为 m 的导体棒 PQ 放 置在导轨上，始终与导轨接触良好，PbcQ 构成矩形。棒与导轨间动摩擦因数为 μ，棒 左侧有两个固定于斜面的光滑立柱。导轨 bc 段长为 L，以 ef 为界，其左侧匀强磁场垂 直斜面向上，右侧匀强磁场方向沿斜面向上，磁感应强度大小均为 B。在 t=0 时，一沿 斜面方向的作用力 F 垂直作用在导轨的 bc 边上，使导轨由静止开始沿斜面向下做匀加 速直线运动，加速度为 a。 （1）请通过计算证明开始一段时间内 PQ 中的电流随时间均匀增大。 （2）求在电流随时间均匀增大的时间 内棒 PQ 横截面内通过的电量 q 和导轨机械能的变化量△E。 （3）请在 F-t 图上定性地画出电流随 时间均匀增大的过程中作用力 F 随时间 t 变化的可能关系图， 并写出相应的条件。（以沿斜面 向下为正方向） JWmVmVWW FFF B 45.0)21(1.02 16.02 1 2 1 222 0 2 1 11 =−+=⇒−=+ smVLkL IRVR VBL R VLBVLBI abbc ababab /2 2 2 22122 ==⇒∆=−= NBILFF abB 4.04.0215.02 =×××=∆== JLFW bcF 4.022 == JWWW FFF 85.04.045.021 =+=+= JWJWW FBFFB 14.06.04.022 −=−−=⇒−=−= s RI WtJWRtIQ FB FB 25.11 2 2 ==⇒=== JmVmVE k 15.02 1 2 1 2 1 2 2 =−=∆ Wt EWW t WP kFFF 8.021 =∆++== WPmVmVWtP BF 8.025.1 )22(1.02 11 2 1 2 1 22 2 0 2 2 = −+ =⇒−=− B B b c d a P Q e f 33．（14 分）（1）I= BLv 2R = BLat 2R 因为BLa 2R 是常数，所以 I∝t，即电流随时间均匀增大。 当 PQ 受到的安培力大于 mgcosθ 时，PQ 会离开斜面，电路不再闭合，回路中会短时无 电 流 。 FA=BIL =B2L2atm 2R = mgcosθ 即 tm=2mgRcosθ B2L2a （2）q= — Itm=1 2 BLatm 2R tm =BLatm2 4R = m2g2Rcos2θ B3L3a ΔE=1 2mv2- mgh =1 2m a tm2（a–gsinθ）= 2m3g2R2cos2θ B4L4a （a–gsinθ） （3）①若 a≥gsinθ-μgcosθ，则 F 始终向下，且随时间均匀增大； ②若 a≤gsinθ-gcosθ，则 F 始终向上，且随时间均匀减小（tm 时 F 仍向上或为零）； ③若 gsinθ-gcosθ＜a＜gsinθ-μgcosθ，则 F 先向上逐渐减小，后向下逐渐增大。 37、（14 分）如图（1），在匀强磁场中有两根倾斜、 长 S=40m 的平行金属导轨，导轨间距 L=1m，导轨 平面与水平面的夹角 θ=300，匀强磁场的磁感应 强度 B=0.3T，垂直导轨平面斜向上。在一个平行 于导轨的变力 F 作用下（F 从零开始增加），一根 质量 m=0.1kg 的导体棒从导轨的顶端由静止开 始沿导轨匀加速下滑，下滑 20m 后撤去变力 F， 导体棒一直下滑至导轨底端。导 体棒始终与导轨垂直，与导轨的动摩擦因数 μ= ， 接在两导轨顶端的电阻 R=3Ω，其他部分电阻均不 计，重力加速度 g 为 10m/s2。求： 3 6 F t O F t O F tO B R 图（1）θ 2010 图（2） F/ N S/mO （1）导体棒下滑 20m 时的速度大小； （2）导体棒下滑 20m 内流过电阻 R 的电量； （3）在图（2）中画出导体棒下滑 20m 内外力 F 随位移 S 变化的图像（在坐标轴上标出关 键点），并求出导体棒下滑 20m 时外力 F 的瞬时功率； （4）撤去外力 F 后导体棒沿轨道下滑，能否最终达到匀速？请通过合理的计算、推导等给 出理由和结论。 （1） ，F 安=0，F=0， ；（2 分） ；（1 分） （2）二解：① ；（公式 2 分，结论 1 分） ② ， （可用 图像围成的面积求）； （公式 2 分，结论 1 分） （3） ；（1 分） 作图：形状对 1 分，坐标对 1 分； ；（1 分） （4）不能。（1 分） 刚撤力 F 时， ，导体棒做加速度不 断减小的减速下滑；（1 分） 若达到匀速： ；（1 分） 若以 加速度一直匀减速下滑，用时 s 达到 m/s，围成面积为 m，大于导 轨剩下的距离 20m（实际下滑过程加速度绝对值逐渐减小，位移大于 m），所以不行。 （1 分） 0ov = 2sin cos 2.5m/sa g gθ µ θ= − = 12 10m/sv as= = 1 2CBLsq R R φ∆= = = 4svt a = = 2C2 BLatq I t tR = ⋅ = ⋅ = I t— 2 2 2=BLv B L aSF F B LR R = =安 2 2 2 3WF B L vP F v R = ⋅ = = 2sin cos 0.5m/sBLvmg mg B L ma aR θ µ θ− − = ⇒ = − 25sin cos 0 m/s3 BLvmg mg B L vR θ µ θ− − = ⇒ =匀 匀 20.5m/s− 10 3 25 3 275 9 275 9