2020届高考数学大二轮复习 第1部分 专题5 立体几何 第2讲 点、直线、平面之间的位置关系练习 10页

第一部分 专题五 第二讲 点、直线、平面之间的位置关系 A组 ‎1．(文)设α，β是两个不同的平面，l，m是两条不同的直线，且l⊂α，m⊂β.( A )‎ A．若l⊥β，则α⊥β B．若α⊥β，则l⊥m C．若l∥β，则α∥β D．若α∥β，则l∥m ‎[解析]　选项A中，平面与平面垂直的判定，故正确；选项B中，当α⊥β时，l，m可以垂直，也可以平行，也可以异面；选项C中，l∥β时，α，β可以相交；选项D中，α∥β时，l，m也可以异面．故选A．‎ ‎(理)设α、β、γ是三个互不重合的平面，m、n为两条不同的直线．给出下列命题：‎ ‎①若n∥m，m⊂α，则n∥α；‎ ‎②若α∥β，n⊄β，n∥α，则n∥β；‎ ‎③若β⊥α，γ⊥α，则β∥γ；‎ ‎④若n∥m，n⊥α，m⊥β，则α∥β.‎ 其中真命题是( C )‎ A．①和②　　　　　　 B．①和③‎ C．②和④ D．③和④‎ ‎[解析]　若n∥m，m⊂α，则n∥α或n⊂α，即命题①不正确，排除A、B；若α∥β，n⊄β，n∥α，则n∥β，则命题②正确，排除D，故应选C．‎ ‎2．如图，在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，下列四个结论不成立的是 ‎( D )‎ A．BC∥平面PDF B．DF⊥平面PAE C．平面PDF⊥平面PAE D．平面PDE⊥平面ABC ‎[解析]　∵D、F分别为AB、AC的中点，∴BC∥DF，‎ 10‎ ‎∵BC⊄平面PDF，∴BC∥平面PDF，故A正确；在正四面体中，∵E为BC中点，易知BC⊥PE，BC⊥AE，∴BC⊥平面PAE，∵DF∥BC，∴DF⊥平面PAE，故B正确；∵DF⊥平面PAE，DF⊂平面PDF，∴平面PDF⊥平面PAE，∴C正确，故选D．‎ ‎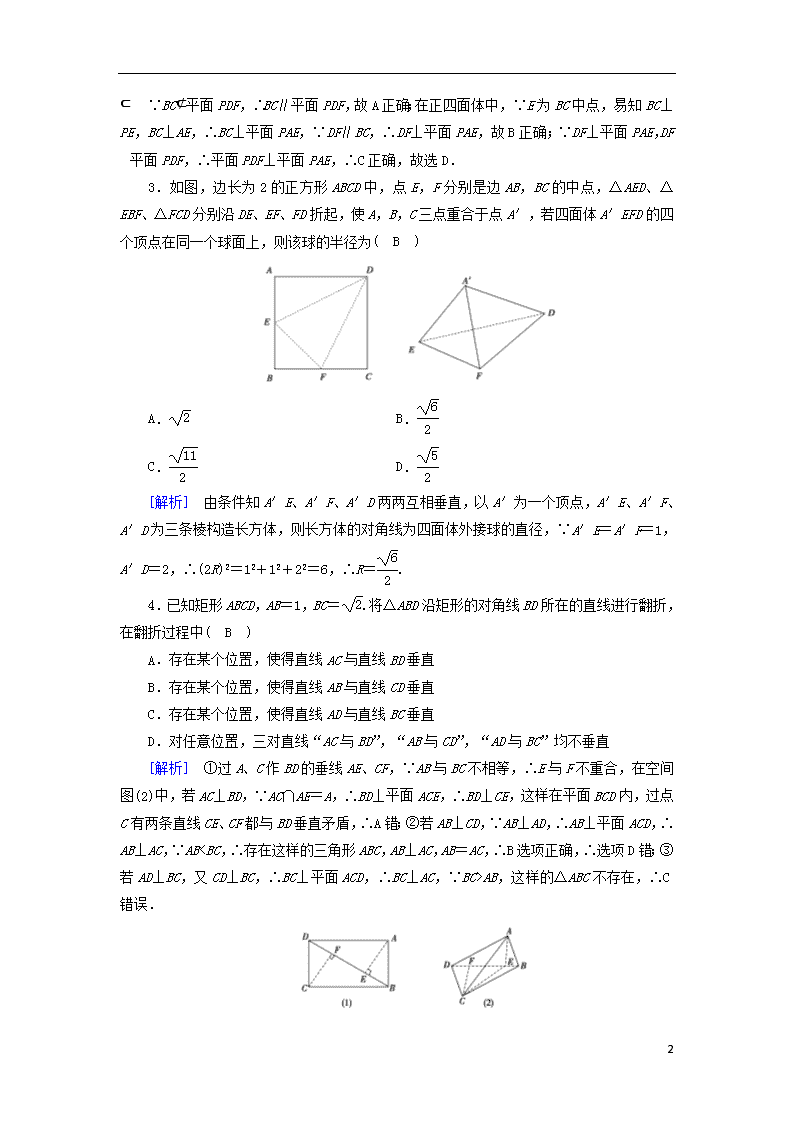3．如图，边长为2的正方形ABCD中，点E，F分别是边AB，BC的中点，△AED、△EBF、△FCD分别沿DE、EF、FD折起，使A，B，C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的半径为( B )‎ A．　　 B．　　　‎ C．　　 D． ‎[解析]　由条件知A′E、A′F、A′D两两互相垂直，以A′为一个顶点，A′E、A′F、A′D为三条棱构造长方体，则长方体的对角线为四面体外接球的直径，∵A′E＝A′F＝1，A′D＝2，∴(2R)2＝12＋12＋22＝6，∴R＝.‎ ‎4．已知矩形ABCD，AB＝1，BC＝.将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中( B )‎ A．存在某个位置，使得直线AC与直线BD垂直 B．存在某个位置，使得直线AB与直线CD垂直 C．存在某个位置，使得直线AD与直线BC垂直 D．对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直 ‎[解析]　①过A、C作BD的垂线AE、CF，∵AB与BC不相等，∴E与F不重合，在空间图(2)中，若AC⊥BD，∵AC∩AE＝A，∴BD⊥平面ACE，∴BD⊥CE，这样在平面BCD内，过点C有两条直线CE、CF都与BD垂直矛盾，∴A错；②若AB⊥CD，∵AB⊥AD，∴AB⊥平面ACD，∴AB⊥AC，∵ABAB，这样的△ABC不存在，∴C错误．‎ 10‎ ‎5．(2018·太原二模)对于不重合的直线m，l和平面α，β，要证α⊥β需具备的条件是( D )‎ A．m⊥l，m∥α，l∥β B．m⊥l，α∩β＝m，l⊂α C．m∥l，m⊥α，l⊥β D．m∥l，l⊥β，m⊂α ‎[解析]　对于A，如图1，可得面α，β不一定垂直，故错；‎ 对于B，如图2，可得面α，β不一定垂直，故错；‎ 对于C，m∥l，m⊥α，l⊥β⇒α∥β，故错；‎ 对于D，有m∥l，l⊥β⇒m⊥β，‎ 又因为m⊂α⇒α⊥β，故正确．‎ ‎6．已知直线l⊥平面α，直线m⊂平面β，则下列四个命题：‎ ‎①α∥β⇒l⊥m；②α⊥β⇒l∥m；‎ ‎③l∥m⇒α⊥β；④l⊥m⇒α∥β.‎ 其中正确命题的序号是①③.‎ ‎[解析]　直线l⊥平面α ，直线m⊂平面β，‎ 当α∥β有l⊥m，故①正确．‎ 当α⊥β有l∥m或l与m异面或相交，故②不正确．‎ 当l∥m有α⊥β，故③正确．‎ 当l⊥m有α∥β或α与β相交，故④不正确．‎ 综上可知①③正确．‎ ‎7．(2018·凉山州二模)在棱长为1的正方体ABCD－A′B′C′D′中，异面直线A′D与AB′所成角的大小是.‎ ‎[解析]　在正方体ABCD－A′B′C′D′中，连接A′D，AB′，B′C，如图所示：‎ 10‎ 则A′B′∥DC，且A′B′＝DC，‎ 所以四边形A′B′CD是平行四边形，‎ 所以A′D∥B′C，‎ 所以∠AB′C是异面直线A′D与AB′所成的角，‎ 连接AC，则△AB′C是边长为的等边三角形，‎ 所以∠AB′C＝，‎ 即异面直线A′D与AB′所成角是.‎ ‎8．设x，y，z为空间不同的直线或不同的平面，且直线不在平面内，下列说法中能保证“若x⊥z，y⊥z，则x∥y”为真命题的序号是①③⑤.‎ ‎①x为直线，y，z为平面；‎ ‎②x，y，z都为平面；‎ ‎③x，y为直线，z为平面；‎ ‎④x，y，z都为直线；‎ ‎⑤x，y为平面，z为直线．‎ ‎[解析]　①x⊥平面z，平面y⊥平面z，‎ 所以x∥平面y或x⊂平面y.‎ 又因为x⊄平面y，故x∥平面y，①成立；‎ ‎②x，y，z均为平面，则x可与y相交，故②不成立；‎ ‎③x⊥平面z，y⊥平面z，x，y为不同直线，故x∥y，③成立；‎ ‎④x，y，z均为直线，则x与y可平行，可异面，也可相交，故④不成立；‎ ‎⑤z⊥x，z⊥y，z为直线，x，y为平面，所以x∥y，⑤成立．‎ ‎9．(文)(2018·全国卷Ⅰ，18)如图，在平行四边形ABCM中，AB＝AC＝3，∠ACM＝90°，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA． ‎ ‎(1)证明：平面ACD⊥平面ABC．‎ ‎(2)Q为线段AD上一点，P为线段BC上一点，且BP＝DQ＝DA，求三棱锥QABP的体积．‎ ‎[解析]　(1)由已知可得，∠BAC＝90°，则BA⊥AC．‎ 10‎ 又BA⊥AD，AD∩AC＝A，所以AB⊥平面ACD．‎ 又AB⊂平面ABC，‎ 所以平面ACD⊥平面ABC．‎ ‎(2)由已知可得，DC＝CM＝AB＝3，DA＝3.‎ 又BP＝DQ＝DA，所以BP＝2.‎ 作QE⊥AC，垂足为E，则QE綊DC＝1.‎ 由已知及(1)可得DC⊥平面ABC，‎ 所以QE⊥平面ABC，‎ 因此，三棱锥QABP的体积为VQABP＝×QE×S△ABP＝×1××3×2sin45°＝1.‎ ‎(理)如图1，在直角梯形ABCD中，AD∥BC, ∠BAD＝，AB＝BC＝AD＝a，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到图2中△A1BE的位置，得到四棱锥A1____BCDE.‎ 图1　　　　　　　　　　　　图2‎ ‎(1)证明：CD⊥平面A1OC；‎ ‎(2)当平面A1BE⊥平面BCDE时，四棱锥A1____BCDE的体积为36，求a的值．‎ ‎[解析]　(1)证明：在题图1中，‎ 因为AB＝BC＝AD＝a，E是AD的中点，‎ ‎∠BAD＝，所以BE⊥AC．‎ 又在题图2中，BE⊥A1O，BE⊥OC，‎ 从而BE⊥平面A1OC．‎ 又BC∥DE且BC＝DE，所以CD∥BE，‎ 所以CD⊥平面A1OC．‎ ‎(2)由已知，平面A1BE⊥平面BCDE，‎ 且平面A1BE∩平面BCDE＝BE，‎ 10‎ ‎ 又由(1)知A1O⊥BE，所以A1O⊥平面BCDE，‎ 即A1O是四棱锥A1BCDE的高．‎ 由题图1可知，A1O＝AB＝a，平行四边形BCDE的面积S＝BC·AB＝a2，‎ 从而四棱锥A1BCDE的体积为 V＝×S×A1O＝×a2×a＝a3，‎ 由a3＝36，得a＝6.‎ B组 ‎1．已知α、β、γ是三个不同的平面，命题“α∥β，且α⊥γ⇒β⊥γ”是真命题，如果把α、β、γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题有( C )‎ A．0个 B．1个 ‎ C．2个 D．3个 ‎[解析]　若α、β换成直线a、b，则命题化为“a∥b，且a⊥γ⇒b⊥γ”，此命题为真命题；若α、γ换为直线a、b，则命题化为“a∥β，且a⊥b⇒b⊥β”，此命题为假命题；若β、γ换为直线a、b，则命题化为“a∥α，且b⊥α⇒a⊥b”，此命题为真命题，故选C．‎ ‎2．设m、n是不同的直线，α、β、γ是不同的平面，有以下四个命题：‎ ‎①⇒β∥γ ②⇒m⊥β ‎③⇒α⊥β ④⇒m∥α 其中，真命题是( C )‎ A．①④ B．②③ ‎ C．①③ D．②④‎ ‎[解析]　①正确，平行于同一个平面的两个平面平行；②错误，由线面平行、垂直定理知：m不一定垂直于β；③正确，由线面平行，垂直关系判断正确；④错误，m也可能在α内．综上所述，正确的命题是①③，故选C．‎ ‎3．已知互不重合的直线a，b，互不重合的平面α，β，给出下列四个命题，错误的命题是( D )‎ A．若a∥α，a∥β，α∩β＝b，则a∥b B．若α⊥β，a⊥α，b⊥β，则a⊥b C．若α⊥β，α⊥γ，β∩γ＝a，则a⊥α D．若α∥β，a∥α，则a∥β ‎[解析]　A中，过直线a作平面γ分别与α，β交于m，n，则由线面平行的性质知a 10‎ ‎∥m∥n，所以m∥α，又由线面平行的性质知m∥b，所以a∥b，正确；B中，由a⊥α，b⊥β，知a，b垂直于两个平面的交线，则a，b所成的角等于二面角的大小，即为90°，所以a⊥b，正确；C中，在α内取一点A，过A分别作直线m垂直于α，β的交线，直线n垂直于α，γ的交线，则由线面垂直的性质知m⊥β，n⊥γ，则m⊥a，n⊥a，由线面垂直的判定定理知a⊥α，正确；D中，满足条件的a也可能在β内，故D错．‎ ‎4．直三棱柱ABC－A1B‎1C1的直观图及三视图如图所示，D为AC的中点，则下列命题是假命题的是( D )‎ A．AB1∥平面BDC1‎ B．A‎1C⊥平面BDC1‎ C．直三棱柱的体积V＝4‎ D．直三棱柱的外接球的表面积为4π ‎[解析]　如图，将直三棱柱ABC－A1B‎1C1补形成正方体，易知A，B，C都正确．故选D．‎ ‎5．a、b表示直线，α、β、γ表示平面．‎ ‎①若α∩β＝a，b⊂α，a⊥b，则α⊥β；‎ ‎②若a⊂α，a垂直于β内任意一条直线，则α⊥β；‎ ‎③若α⊥β，α∩γ＝a，β∩γ＝b，则a⊥b；‎ ‎④若a不垂直于平面α，则a不可能垂直于平面α内无数条直线；‎ ‎⑤若l⊂α，m⊂α，l∩m＝A，l∥β，m∥β，则α∥β.‎ 其中为真命题的是②⑤.‎ ‎[解析]　对①可举反例如图，需b⊥β才能推出α⊥β.对③可举反例说明，当γ不与α，β的交线垂直时，即可得到a，b不垂直；④对a只需垂直于α内一条直线便可以垂直α内无数条与之平行的直线．所以只有②⑤是正确的．‎ 10‎ ‎6．在三棱锥C－ABD中(如图)，△ABD与△CBD是全等的等腰直角三角形，O为斜边BD的中点，AB＝4，二面角A－BD－C的大小为60°，并给出下面结论：①AC⊥BD；②AD⊥CO；③△AOC为正三角形；④cos∠ADC＝.其中真命题是①③.(填序号)‎ ‎[解析]　对于①，因为△ABD与△CBD是全等的等腰直角三角形，O为斜边BD的中点，所以CO⊥BD，AO⊥BD，AO∩OC＝O，所以BD⊥平面AOC，所以AC⊥BD，因此①正确；对于②，假设CO⊥AD，又CO⊥BD，可得CO⊥平面ABD，由①可得：∠AOC是二面角A－BD－C的平面角，这与已知二面角A－BD－C为60°矛盾，因此不正确；对于③，由△ABD与△CBD是全等的等腰直角三角形，O为斜边BD的中点，所以OC＝OA，由①可得：∠AOC是二面角A－BD－C的平面角且为60°，所以△AOC为正三角形，因此③正确；对于④，AB＝4，由③可得：AC＝OA＝2，AD＝CD＝4，所以cos∠ADC＝＝≠，因此不正确；综上可得：只有①③正确．‎ ‎7．如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边相等，M是PC上的一动点，请你补充一个条件①(或③)，使平面MBD⊥平面PCD．①DM⊥PC；②DM⊥BM；③BM⊥PC；④PM＝MC(填写你认为是正确的条件对应的序号)．‎ ‎[解析]　因为在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，‎ M是PC上的一动点，‎ 所以BD⊥PA，BD⊥AC，‎ 因为PA∩AC＝A，所以BD⊥平面PAC，所以BD⊥PC．‎ 所以当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD．‎ 10‎ 而PC⊂平面PCD，所以平面MBD⊥平面PCD．‎ ‎8．如图：在四棱锥P－ABCD中，底面ABCD是菱形，∠ABC＝60°PA⊥平面ABCD，点M，N分别为BC，PA的中点，且PA＝AB＝2.‎ ‎(1)证明：BC⊥平面AMN；‎ ‎(2)求三棱锥N－AMC的体积；‎ ‎(3)在线段PD上是否存在一点E，使得NM∥平面ACE；若存在，求出PE的长，若不存在，说明理由．‎ ‎[解析]　(1)因为ABCD为菱形，所以AB＝BC，‎ 又∠ABC＝60°，所以AB＝BC＝AC，‎ 又M为BC中点，所以BC⊥AM 而PA⊥平面ABCD，BC⊂平面ABCD，所以PA⊥BC，‎ 又PA∩AM＝A，所以BC⊥平面AMN.‎ ‎(2)因为S△AMC＝AM·CM＝××1＝，‎ 又PA⊥底面ABCD，PA＝2，所以AN＝1，‎ 所以，三棱锥N－AMC的体积V＝S△AMC·AN ‎＝××1＝.‎ ‎(3)存在 取PD中点E，连结NE，EC，AE，‎ 因为N，E分别为PA，PD中点，所以NE綊AD 又在菱形ABCD中，CM綊AD，‎ 所以NE綊MC，即MCEN是平行四边形，所以NM∥EC，‎ 又EC⊂平面ACE，NM⊄平面ACE，所以MN∥平面ACE，‎ 即在PD上存在一点E，使得NM∥平面ACE，‎ 此时PE＝PD＝.‎ ‎9．(2018·全国卷Ⅲ，19)如图，矩形ABCD所在平面与半圆弧所在平面垂直，M是上异于C，D的点．‎ 10‎ ‎(1)证明：平面AMD⊥平面BMC．‎ ‎(2)在线段AM上是否存在点P，使得MC∥平面PBD？说明理由．‎ ‎[解析]　(1)由题设知，平面CMD⊥平面ABCD，交线为CD．‎ 因为BC⊥CD，BC⊂平面ABCD，所以BC⊥平面CMD，故BC⊥DM.‎ 因为M为上异于C，D的点，且DC为直径，‎ 所以 DM⊥CM.‎ 又 BC∩CM＝C，所以DM⊥平面BMC．‎ 而DM⊂平面AMD，故平面AMD⊥平面BMC．‎ ‎(2)存在，AM的中点即为符合题意的点P.证明如下：‎ 取AM的中点P，连接AC，BD交于点N，连接PN.‎ 因为ABCD是矩形，‎ 所以N是AC的中点，‎ 在△ACM中，点P，N分别是AM，AC的中点，‎ 所以PN∥MC，‎ 又因为PN⊂平面PBD，MC⊄平面PBD，‎ 所以MC∥平面PBD，‎ 所以，在线段AM上存在点P，即AM的中点，使得MC∥平面PBD．‎ 10‎