2013高考数学理热点专题专练专题六 算法统计概率复数测试题 17页

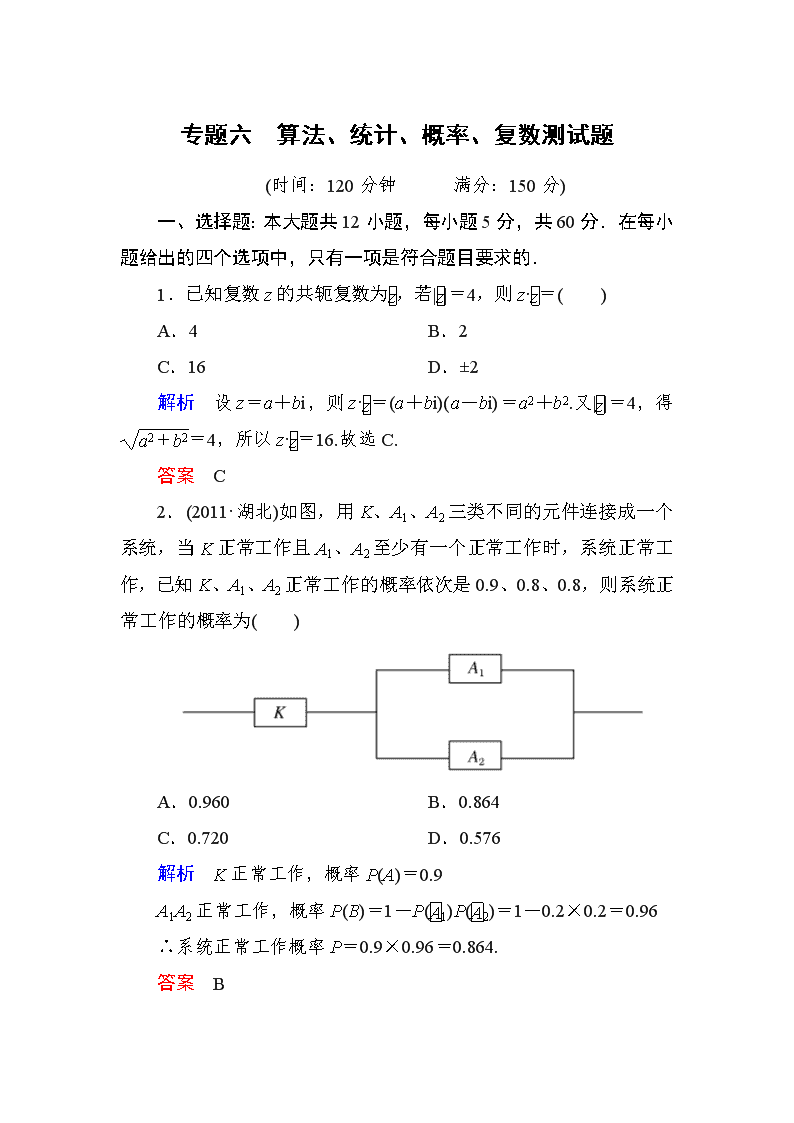
专题六　算法、统计、概率、复数测试题 ‎(时间：120分钟　　　满分：150分)‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知复数z的共轭复数为，若||＝4，则z·＝(　　)‎ A．4　　　　　　　　　　 B．2‎ C．16 D．±2‎ 解析　设z＝a＋bi，则z·＝(a＋bi)(a－bi)＝a2＋b2.又||＝4，得＝4，所以z·＝16.故选C.‎ 答案　C ‎2．(2011·湖北)如图，用K、A1、A2三类不同的元件连接成一个系统，当K正常工作且A1、A2至少有一个正常工作时，系统正常工作，已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8，则系统正常工作的概率为(　　)‎ A．0.960 B．0.864‎ C．0.720 D．0.576‎ 解析　K正常工作，概率P(A)＝0.9‎ A‎1A2正常工作，概率P(B)＝1－P(1)P(2)＝1－0.2×0.2＝0.96‎ ‎∴系统正常工作概率P＝0.9×0.96＝0.864.‎ 答案　B ‎3．(2011·课标)有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为(　　)‎ A. B. C. D. 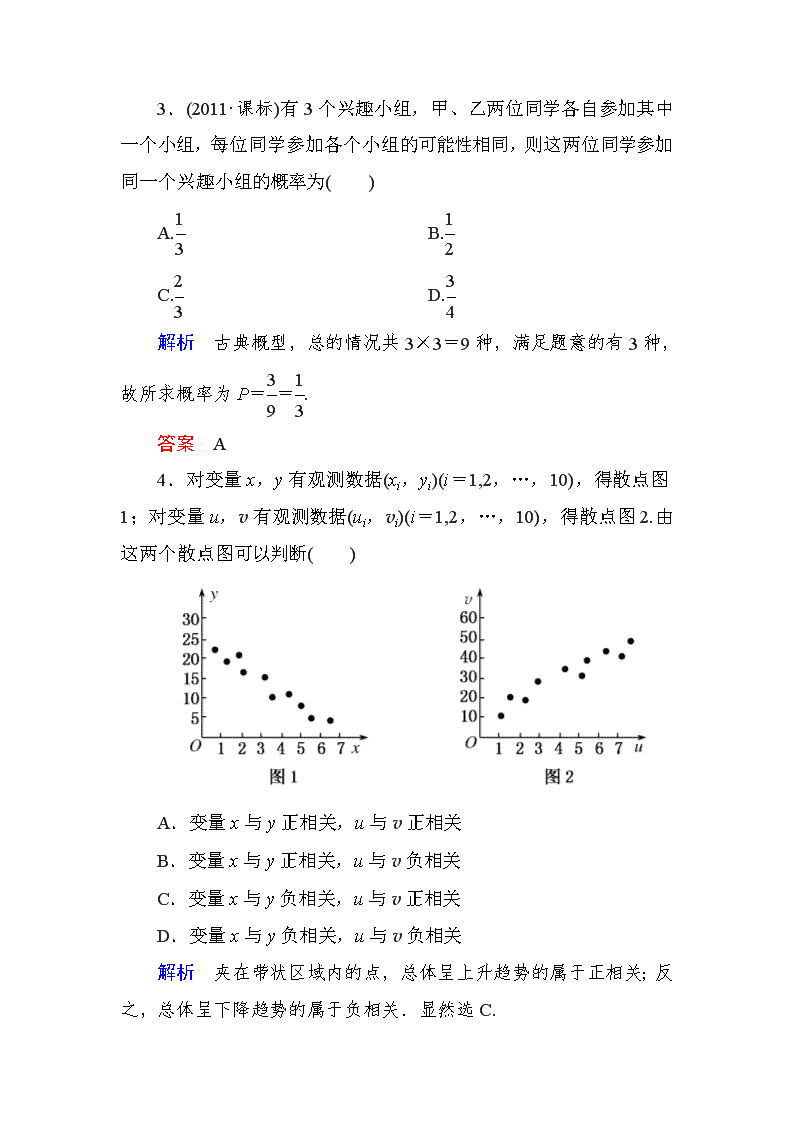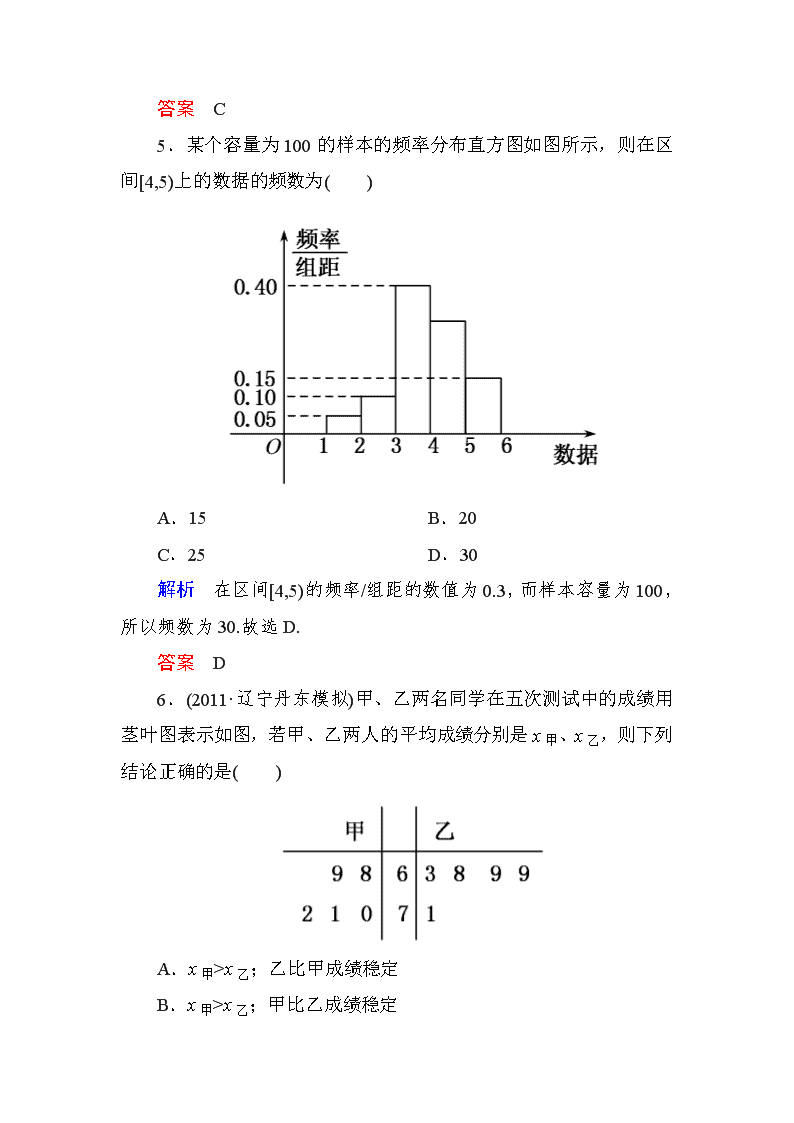解析　古典概型，总的情况共3×3＝9种，满足题意的有3种，故所求概率为P＝＝.‎ 答案　A ‎4．对变量x，y有观测数据(xi，yi)(i＝1,2，…，10)，得散点图1；对变量u，v有观测数据(ui，vi)(i＝1,2，…，10)，得散点图2.由这两个散点图可以判断(　　)‎ A．变量x与y正相关，u与v正相关 B．变量x与y正相关，u与v负相关 C．变量x与y负相关，u与v正相关 D．变量x与y负相关，u与v负相关 解析　夹在带状区域内的点，总体呈上升趋势的属于正相关；反之，总体呈下降趋势的属于负相关．显然选C.‎ 答案　C ‎5．某个容量为100的样本的频率分布直方图如图所示，则在区间[4,5)上的数据的频数为(　　)‎ A．15 B．20‎ C．25 D．30‎ 解析　在区间[4,5)的频率/组距的数值为0.3，而样本容量为100，所以频数为30.故选D.‎ 答案　D ‎6．(2011·辽宁丹东模拟)甲、乙两名同学在五次测试中的成绩用茎叶图表示如图，若甲、乙两人的平均成绩分别是x甲、x乙，则下列结论正确的是(　　)‎ A．x甲>x乙；乙比甲成绩稳定 B．x甲>x乙；甲比乙成绩稳定 C．x甲x乙．又s＝×(22＋12＋02＋12＋22)＝×10＝2，s＝×(52＋02＋12＋12＋32)＝×36＝7.2，所以甲比乙成绩稳定．故选B.‎ 答案　B ‎7．(2012·福建)如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率是(　　)‎ A. B. C. D. 解析　由图示可得，图中阴影部分的面积S＝(－x)dx＝＝－＝，由此可得点P恰好取自阴影部分的概率P＝＝.‎ 答案　C ‎8．如图所示的流程图，最后输出的n的值是(　　)‎ A．3 B．4‎ C．5 D．6‎ 解析　当n＝2时，22>22不成立；当n＝3时，23>32不成立；当n＝4时，24>42不成立；当n＝5时，25>52成立．所以n＝5.故选C.‎ 答案　C ‎9．正四面体的四个表面上分别写有数字1,2,3,4，将3个这样的四面体同时投掷于桌面上，与桌面接触的三个面上的数字的乘积能被3整除的概率为(　　)‎ A. B. C. D. 解析　将正四面体投掷于桌面上时，与桌面接触的面上的数字是1,2,3,4的概率是相等的，都等于.若与桌面接触的三个面上的数字的乘积能被3整除，则三个数字中至少应有一个为3，其对立事件为“与桌面接触的三个面上的数字都不是‎3”‎，其概率是3＝，故所求概率为1－＝.‎ 答案　C ‎10．用系统抽样法从160名学生中抽取容量为20的样本，将160名学生随机地从1～160编号，按编号顺序平均分成20组(1～8号，9～16号，…，153～160号)，若第16组抽出的号码为126，则第1组中用抽签的方法确定的号码是(　　)‎ A．5 B．6‎ C．7 D．8‎ 解析　设第1组抽出的号码为x，则第16组应抽出的号码是8×15＋x＝126，∴x＝6.故选B.‎ 答案　B ‎11．(2011·杭州市第一次教学质量检测)体育课的排球发球项目考试的规则是：每位学生最多可发球3次，一旦发球成功，则停止发球，否则一直发到3次为止．设学生一次发球成功的概率为p(p≠0)，发球次数为X，若X的数学期望E(X)>1.75，则p的取值范围是(　　)‎ A. B. C. D. 解析　发球次数X的分布列如下表，‎ X ‎1‎ ‎2‎ ‎3‎ P p ‎(1－p)p ‎(1－p)2‎ 所以期望E(X)＝p＋2(1－p)p＋3(1－p)2>1.75，‎ 解得p>(舍去)或p<，又p>0，故选C.‎ 答案　C ‎12．(2012·济宁一中高三模拟)某计算机程序每运行一次都随机出现一个五位的二进制数A＝，其中A的各位数中，a1＝1，ak(k可取2,3,4,5)出现0的概率为，出现1的概率为.记ξ＝a1＋a2＋a3＋a4＋a5，当程序运行一次时，ξ的数学期望E(ξ)＝(　　)‎ A. B. C. D. 解析　ξ＝1，P1＝C40＝，‎ ξ＝2时，P2＝C3·＝，‎ ξ＝3时，P3＝C·2·2＝，‎ ξ＝4时，P4＝C·3＝，‎ ξ＝5时，P5＝C4＝，‎ E(ξ)＝1×＋2×＋3×＋4×＋5×＝.‎ 答案　C 二、填空题：本大题共4小题，每小题4分，共16分，将答案填在题中的横线上．‎ ‎13．(2012·广东湛江十中模拟)在可行域内任取一点，规则如流程图所示，则能输出数对(x，y)的概率为________．‎ 解析　如图所示，给出的可行域即为正方形及其内部．而所求事件所在区域为一个圆，两面积相比即得概率为.‎ 答案　 ‎14．(2012·山东潍坊模拟)给出下列命题：‎ ‎(1)若z∈C，则z2≥0；(2)若a，b∈R，且a>b，则a＋i>b＋i；(3)若a∈R，则(a＋1)i是纯虚数；(4)若z＝，则z3＋1对应的点在复平面内的第一象限．其中正确的命题是________．‎ 解析　由复数的概念及性质知，(1)错误；(2)错误；(3)错误，若a＝－1，(a＋1)i＝0；(4)正确，z3＋1＝(－i)3＋1＝i＋1.‎ 答案　(4)‎ ‎15．(2011·上海)随机抽取的9位同学中，至少有2位同学在同一月份出生的概率为________．(默认每个月的天数相同，结果精确到0.001)‎ 解析　P＝1－≈0.985.‎ 答案　0.985‎ ‎16．若某程序框图如图所示，则该程序运行后输出的y等于________．‎ 解析　由图中程序框图可知，所求的y是一个“累加的运算”，即第一步是3；第二步是7；第三步是15；第四步是31；第五步是63.‎ 答案　63‎ 三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．(本小题满分12分)‎ 某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示：‎ 积极参加 班级工作 不太主动参加 班级工作 合计 学习积极性高 ‎18‎ ‎7‎ ‎25‎ 学习积极性一般 ‎6‎ ‎19‎ ‎25‎ 合计 ‎24‎ ‎26‎ ‎50‎ ‎(1)如果随机抽查这个班的一名学生，那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？‎ ‎(2)试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由．(参考下表)‎ P(K2≥k)‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 解　(1)积极参加班级工作的学生有24人，总人数为50人，概率为＝；不太主动参加班级工作且学习积极性一般的学生有19人，概率为.‎ ‎(2)K2＝＝≈11.5，‎ ‎∵K2>10.828，‎ ‎∴有99.9%的把握说学生的学习积极性与对待班级工作的态度有关系．‎ ‎18．(本小题满分12分)‎ 在1996年美国亚特兰大奥运会上，中国香港风帆选手李丽珊以惊人的耐力和斗志，勇夺金牌，为香港体育史揭开了“突破零”的新一页．在风帆比赛中，成绩以低分为优胜．比赛共11场，并以最佳的9场成绩计算最终的名次．前7场比赛结束后，排名前5位的选手积分如表一所示：‎ 表一 排名 运动员 比赛场次 总分 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎1‎ 李丽珊 ‎(中国香港)‎ ‎3‎ ‎2‎ ‎2‎ ‎2‎ ‎4‎ ‎2‎ ‎7‎ ‎22‎ ‎2‎ 简度(新西兰)‎ ‎2‎ ‎3‎ ‎6‎ ‎1‎ ‎10‎ ‎5‎ ‎5‎ ‎32‎ ‎3‎ 贺根(挪威)‎ ‎7‎ ‎8‎ ‎4‎ ‎4‎ ‎3‎ ‎1‎ ‎8‎ ‎35‎ ‎4‎ 威尔逊(英国)‎ ‎5‎ ‎5‎ ‎14‎ ‎5‎ ‎5‎ ‎6‎ ‎4‎ ‎44‎ ‎5‎ 李科(中国)‎ ‎4‎ ‎13‎ ‎5‎ ‎9‎ ‎2‎ ‎7‎ ‎6‎ ‎46‎ 根据上面的比赛结果，我们如何比较各选手之间的成绩及稳定情况呢？如果此时让你预测谁将获得最后的胜利，你会怎么看？‎ 解　由表一，我们可以分别计算5位选手前7场比赛积分的平均数和标准差，分别作为衡量各选手比赛的成绩及稳定情况，如表二所示．‎ 表二 排名 运动员 平均积分()‎ 积分标准差(s)‎ ‎1‎ 李丽珊(中国香港)‎ ‎3.14‎ ‎1.73‎ ‎2‎ 简度(新西兰)‎ ‎4.57‎ ‎2.77‎ ‎3‎ 贺根(挪威)‎ ‎5.00‎ ‎2.51‎ ‎4‎ 威尔逊(英国)‎ ‎6.29‎ ‎3.19‎ ‎5‎ 李科(中国)‎ ‎6.57‎ ‎3.33‎ 从表二中可以看出：李丽珊的平均积分及积分标准差都比其他选手的小，也就是说，在前7场比赛过程中，她的成绩最为优异，而且表现也最为稳定．‎ 尽管此时还有4场比赛没有进行，但这里我们可以假定每位运动员在各自的11场比赛中发挥的水平大致相同(实际情况也确实如此)，因此可以把前7场比赛的成绩看做是总体的一个样本，并由此估计每位运动员最后的比赛的成绩．从已经结束的7场比赛的积分来看，李丽珊的成绩最为优异，而且表现最为稳定，因此在后面的4场比赛中，我们有足够的理由相信她会继续保持优异而稳定的成绩，获得最后的冠军．‎ ‎19．(本小题满分12分)‎ ‎(2012·苏州五中模拟)设不等式组表示的区域为A，不等式组表示的区域为B，在区域A中任意取一点P(x，y)．‎ ‎(1)求点P落在区域B中的概率；‎ ‎(2)若x、y分别表示甲、乙两人各掷一次正方体骰子所得的点数，求点P落在区域B中的概率．‎ 解　(1)设区域A中任意一点P(x，y)∈B为事件M.因为区域A的面积为S1＝36，区域B在区域A中的面积为S2＝18.故P(M)＝＝.‎ ‎(2)设点P(x，y)落在区域B中为事件N，甲、乙两人各掷一次骰子所得的点P(x，y)的个数为36，其中在区域B中的点P(x，y)有21个．故P(N)＝＝.‎ ‎20．(本小题满分12分)‎ 某中学部分学生参加全国高中数学竞赛，取得了优异成绩，指导老师统计了所有参赛同学的成绩(成绩都为整数，试题满分120分)，并且绘制了“频率分布直方图”(如图)，请回答：‎ ‎(1)该中学参加本次数学竞赛的有多少人？‎ ‎(2)如果90分以上(含90分)获奖，那么获奖率是多少？‎ ‎(3)这次竞赛成绩的中位数落在哪段内？‎ ‎(4)上图还提供了其他信息，请再写出两条．‎ 解　(1)由直方图(如图)可知：4＋6＋8＋7＋5＋2＝32(人)；‎ ‎(2)90分以上的人数为7＋5＋2＝14(人)，‎ ‎∴×100%＝43.75%.‎ ‎(3)参赛同学共有32人，按成绩排序后，第16个、第17个是最中间两个，而第16个和第17个都落在80～90之间．‎ ‎∴这次竞赛成绩的中位数落在80～90之间．‎ ‎(4)①落在80～90段内的人数最多，有8人；‎ ‎②参赛同学的成绩均不低于60分．‎ ‎21．(本小题满分12分)‎ ‎(2012·天津)现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择．为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．‎ ‎(1)求这4个人中恰有2人去参加甲游戏的概率；‎ ‎(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；‎ ‎(3)用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ξ＝|X－Y|，求随机变量ξ的分布列与数学期望Eξ.‎ 解　依题意，这4个人中，每个人去参加甲游戏的概率为，去参加乙游戏的概率为.设“这4个人中恰有i人去参加甲游戏”为事件Ai(i＝0,1,2,3,4)，则P(Ai)＝Ci4－i.‎ ‎(1)设4个人中恰有2人去参加甲游戏的概率为P(A2)‎ P(A2)＝C22＝.‎ ‎(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B，则B＝A3∪A4，由于A3和A4互斥，故 P(B)＝P(A3)＋P(A4)＝C3＋C4＝.‎ 所以，这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为.‎ ‎(3)ξ的所有可能取值为0,2,4.‎ 由于A1与A3互斥，A0和A4互斥，故 P(ξ＝0)＝P(A2)＝，‎ P(ξ＝2)＝P(A1)＋P(A3)＝，‎ P(ξ＝4)＝P(A0)＋P(A4)＝.‎ 所以ξ的分布列是 ξ ‎0‎ ‎2‎ ‎4‎ P 随机变量ξ的数学期望Eξ＝0×＋2×＋4×＝.‎ ‎22．(本小题满分14分)‎ ‎(2012·福建)受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：‎ 品牌 甲 乙 首次出现故 障时间x(年)‎ ‎02‎ ‎02‎ 轿车数 量(辆)‎ ‎2‎ ‎3‎ ‎45‎ ‎5‎ ‎45‎ 每辆利 润(万元)‎ ‎1‎ ‎2‎ ‎3‎ ‎1.8‎ ‎2.9‎ 将频率视为概率，解答下列问题：‎ ‎(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保障期内的概率；‎ ‎(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列；‎ ‎(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．‎ 解　(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A.则P(A)＝＝.‎ ‎(2)依题意得，X1的分布列为 X1‎ ‎1‎ ‎2‎ ‎3‎ P X2的分布列为 X2‎ ‎1.8‎ ‎2.9‎ P ‎(3)由(2)得，‎ E(X1)＝1×＋2×＋3×＝＝2.86(万元)，‎ E(X2)＝1.8×＋2.9×＝2.79(万元)．‎ 因为E(X1)>E(X2)，所以应生产甲品牌轿车．‎