高考数学空间向量与立体几何总复习 14页

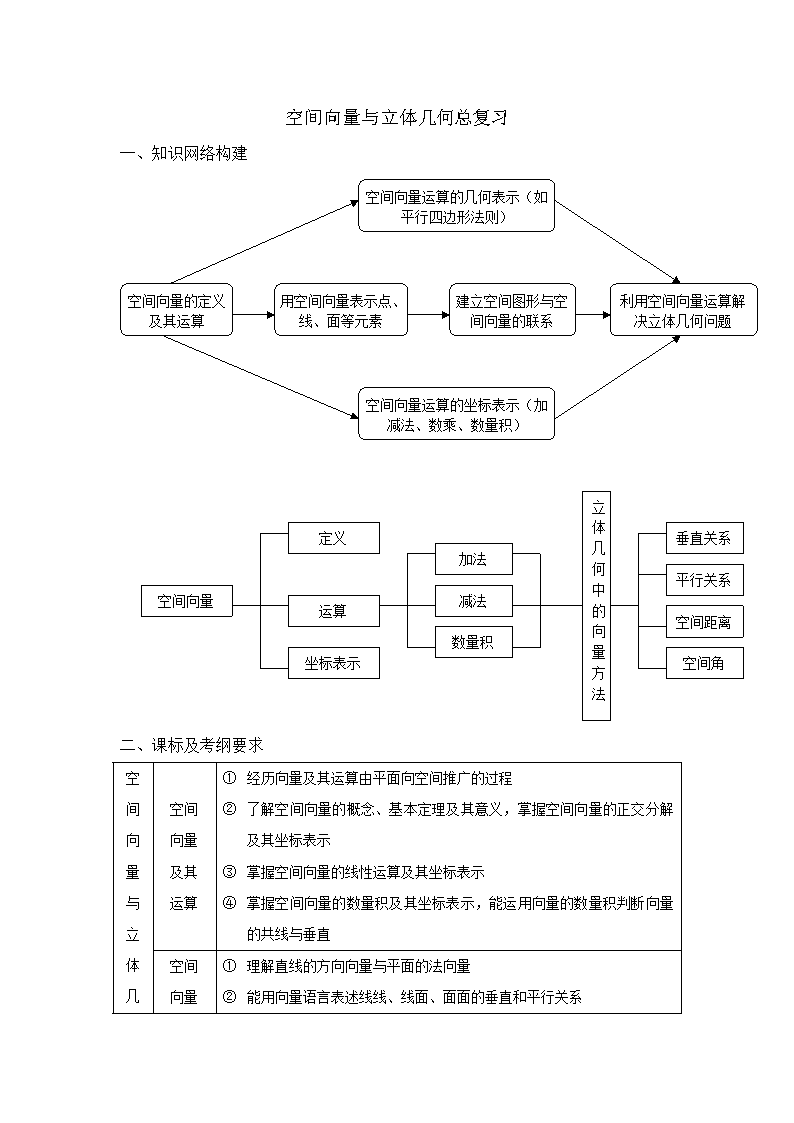
空间向量与立体几何总复习 一、知识网络构建 空间向量的定义及其运算 空间向量运算的几何表示（如平行四边形法则）‎ 用空间向量表示点、线、面等元素 建立空间图形与空间向量的联系 利用空间向量运算解决立体几何问题 空间向量运算的坐标表示（加减法、数乘、数量积）‎ 空间向量 定义 运算 坐标表示 加法 减法 数量积 立体几何中的向量方法 垂直关系 平行关系 空间距离 空间角 二、课标及考纲要求 空间 向量 及其 运算 ① 经历向量及其运算由平面向空间推广的过程 ② 了解空间向量的概念、基本定理及其意义，掌握空间向量的正交分解及其坐标表示 ③ 掌握空间向量的线性运算及其坐标表示 ④ 掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直 空间向量与立体几何 空间 向量 ① 理解直线的方向向量与平面的法向量 ② 能用向量语言表述线线、线面、面面的垂直和平行关系 的运 用 ③ 能用向量方法证明有关线、面位置关系的一些定理 ④ 能用向量方法解决线线、线面、面面的夹角的计算问题，体会向量方法在研究几何问题中的作用 三、知识要点及考点精析 ‎（一）空间向量及其运算 ‎1．空间向量的概念 在空间，我们把具有大小和方向的量叫做空间向量，向量的大小叫做向量的长度或模．‎ 还需要掌握的几个相关的概念包括相等向量、零向量、共线向量等．‎ ‎2．空间向量的线性运算 ‎（1）空间向量的加法、减法和数乘运算 平面向量中的三角形法则和平行四边形法则同样适用于空间向量的加（减）法运算．加法运算对于有限个向量求和，交换相加向量的顺序其和不变．三个不共面的向量的和等于以这三个向量为邻边的平行六面体的对角线所表示的向量．加法和数乘运算满足运算律：‎ ‎①交换律，即；‎ ‎②结合律，即；‎ ‎③分配律，即及（其中均为实数）．‎ ‎（2）空间向量的基本定理 ‎① 共线向量定理：对空间向量的充要条件是存在实数，使．‎ ‎② 共面向量定理：如果空间向量不共线，则向量c与向量共面的充要条件是，存在惟一的一对实数，使．‎ ‎③ 空间向量基本定理：如果三个向量a, b, c不共面，那么对空间任一向量p，存在有序实数组，，，使．其中是空间的一个基底，a, b, c都叫做基向量，该定理可简述为：空间任一向量p都可以用一个基底惟一线性表示（线性组合）．‎ ‎（3）两个向量的数量积 两个向量的数量积是ab= |a||b|cos，数量积有如下性质： a, b, c ‎① ae= |a|cos（e为单位向量）；‎ ‎② aaab=；‎ ‎③ aa=|a|2；‎ ‎④ |ab|| a||b|．‎ 数量积运算满足运算律：‎ ‎①交换律，即ab= ba；‎ ‎②与数乘的结合律，即（a）b=（ab）；‎ ‎③分配律，即（a+b）c =ac +bc．‎ ‎3．空间向量的坐标运算 ‎（1）给定空间直角坐标系和向量a，存在惟一的有序实数组使，则叫作向量a在空间的坐标，记作．‎ ‎（2）空间向量的直角坐标运算律 ‎①若，则 ‎，，ab．‎ ‎，．‎ ‎②若，则．即一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标．‎ ‎4．直线的方向向量与向量方程 ‎（１）位置向量：已知向量a，在空间固定一个基点，作向量，则点在空间的位置被a所惟一确定，a称为位置向量．‎ ‎（２）方向向量与向量方程：给定一个定点和一个向量a，再任给一个实数，以为起点作向量a，则此向量方程称为动点对应直线的参数方程，向量a称为直线的方向向量．‎ 典型例题分析：‎ 例1．若=(,1,3),=(1,-,9),如果与为共线向量,则( )‎ A．， B．, C．, ‎ D．,‎ 答案: C 例2．已知向量a＝(1，1，0)，b＝(-1，0，2)，且a＋b与‎2 a-b互相垂直，则的值是( )‎ A． 1 B． C． D． ‎ 答案: D 例3．已知=(2,2,1),=(4,5,3),求平面ABC的单位法向量．‎ 解:设平面ABC的法向量n=(x,y,1),则n⊥且n⊥,即n·=0,且n·=0,即 ‎ 即 ∴n=(,-1,1),单位法向量n=±(,-,)．‎ ‎（二）立体几何中的向量方法 ‎1．利用向量法确定直线、平面间的平行、垂直等位置关系 设直线的方向向量是，直线的方向向量是，平面的法向量是，平面的法向量是，则有如下结论成立： ‎ ‎（1）u1∥u2u1； ‎ ‎（2）；‎ ‎（3）∥；‎ ‎（4）；‎ ‎（5）；‎ ‎（6）．‎ 第一部分：平行问题 ‎① 利用空间向量解决线线平行问题 ‎（06山东模拟）已知直线平面，直线平面，为垂足．求证：．‎ 证明：以点为原点，以射线为非负轴，如图1，建立空间直角坐标系，为沿轴的单位向量，且设．‎ ‎，，，，‎ ‎．‎ ‎，．，即．‎ 点评：由向量的共线的充要条件知，只要证明即可．‎ ‎② 利用空间向量解决线面平行问题 ‎（06山西模拟）已知是正三棱柱，是的中点，求证：平面．‎ 证法1：建立如图2的空间直角坐标系．设正三棱柱的底面边长为，侧棱长为，‎ 则．‎ 设平面的法向量为，‎ 则．‎ 由，，得 取得，得．‎ 由，‎ 得，即平面．‎ 证法2：如图3，记，‎ 则．‎ ‎，共面．‎ 又平面，平面．‎ 点评：用向量证明线面平行问题通常有两种方法：①向量与两个不共线的向量共面的充要条件是存在惟一的有序实数对，使．利用共面向量定理可证明线面平行问题，如证法2．②设为平面的法向量，要证明，只需证明，如证法1．‎ ‎③ 利用空间向量解决面面平行问题 例题：已知正方体的棱长为1，分别为的中点，求证：平面平面．‎ 证明：建立空间直角坐标系，‎ 则．‎ 得．‎ 设为平面的法向量，设为平面的法向量．‎ 空间计算：．‎ 由，得平面平面．‎ 点评：设分别为平面的法向量，要证，只需证明：存在一个非零常数，满足，则．其实本题也可转化为线线平行，则面面平行．即用向量先证明，，则有线面平行，从而平面平面．‎ 第二部分：垂直问题 ‎① 利用空间向量解决线线垂直问题 ‎（2003年高考题）已知正四棱，，点为中点，点为中点．证明：为与的公垂线．‎ 证明：如图1，在以为的原点的空间直角坐标系中，‎ ‎．‎ 由，，‎ 得．‎ 为与的公垂线．‎ 点评：把推理论证（）用向量运算（）来代替，减少了构造辅助图形，降低了思维量．‎ ‎② 利用空间向量解决线面垂直问题 ‎（2005年高考题）如图2，在四棱锥中，底面为矩形，侧棱底面，为的中点，在侧面内找一点，使面 ‎ 解：如图2，在以为原点的空间直角坐标系中，‎ ‎．‎ 设．‎ 由面，得 即 ．‎ 点评：按照传统方法，要构造三条辅助线，多解两个三角形，画图、看图以及计算都增加了难度．用空间向量的观点处理立体几何中的线面关系，把几何问题代数化，降低了难度．‎ ‎③ 利用空间向量解决面面垂直问题 ‎（07北京海淀）如图3，在正方体中，为与的交点，为的中点，求证：平面平面．‎ 分析：要证明平面平面，只要证明平面内的一条直线垂直于平面 中的两条相交直线即可，而从图中观察，证较容易成功．‎ 证明：设．‎ 则．‎ 而，‎ ‎，‎ ‎，‎ ‎，‎ ‎．‎ ‎，．‎ 又，平面．‎ 又平面，‎ 平面平面． ‎ 点评：向量a垂直于向量b的充要条件是ab，据此可以证明直线与直线垂直，进而还可证明直线与平面垂直及两个平面垂直．在证明一对向量垂直时，往往用一组基底先表示这一对向量，再考虑它们的数量积是否为零．‎ ‎2．利用空间向量解决空间距离问题 ‎（1）利用空间向量求线线距离 如图1，若是异面直线的公垂线段，分别为上的任意两点．‎ 则两异面直线间的距离为 ‎（其中与垂直，分别为两异面直线上的任意两点）．‎ 例题：如图2，在正方体中，为的中点．求异面直线和间的距离？‎ 解析：设正方体棱长为2，以为原点，建立如图2所示的空间直角坐标系，‎ 则．‎ 设和公垂线段上的向量为，‎ 则即 ‎．‎ 又，，‎ 所以异面直线和间的距离为．‎ ‎（2）利用空间向量求点面距离 如图3，已知为平面的一条斜线段，为平面的法向量．‎ 则点到平面的距离．‎ 例题：如图4，已知是各条棱长均等于的正三棱柱，是侧棱的中点．求 点到平面的距离．‎ 解析：为正方形，．‎ 易得平面平面，‎ 面，‎ 是平面的一个法向量．‎ 设点是平面的距离为，‎ 则 ‎（3）利用空间向量求线面、面面距离 注意：利用空间向量求线面、面面距离的问题显然可以转换成利用空间向量求点面距离的问题 例题：如图5，已知边长为的正三角形中，分别为和的中点，面，且，设平面为且与平行．求与平面间的距离？‎ 解析：设的单位向量分别为，选取作为空间向量的一个基底．‎ 易知，‎ ‎．‎ 设是平面的一个法向量，‎ 则．‎ 即．‎ 直线与平面间的距离．‎ 例题：如图6，在棱长为1的正方体中．求平面与平面间的距离．‎ 解析：建立如图所示的空间直角坐标系，易知平面与平面平行．‎ 设平面的一个法向量，‎ 则，即 ‎．‎ 平面与平面间的距离．‎ ‎3．利用空间向量解决空间角问题 ‎（1）利用空间向量求线线角 设两异面直线所成的角为分别是 的方向向量，注意到异面直线所成角的范围是，则有．‎ ‎（2006广东模拟）已知正方形和矩形所在平面互相垂直，．试在线段 上确定一点，使得与所成的角是．‎ 如图1，建立空间直角坐标系，则．‎ 设，得．‎ 又和所成的角是，‎ ‎．‎ 解得或（舍去），即点是的中点．‎ 点评：采用传统的平移法求异面直线所成角的大小，免不了要作辅助线和几何推理．这里运用向量法，没有了这些手续，显得便当快捷．‎ ‎（2）利用空间向量求线面角 如图2，点在平面外，为内一点，斜线和平面所成的角为，为的一个法向量，注意到斜线和平面所成角的范围是，则有，结合向量的夹角公式便可求．‎ ‎（05山东模拟）在正三棱柱中，已知在棱上，‎ 且，若与平面所成的角为，则sin（　　）‎ Ａ． Ｂ． Ｃ． Ｄ． ‎ 解：取中点，连结，则，如图3，建立空间直角坐标系，则，则．‎ 平面平面，，‎ 平面．‎ 为平面的一个法向量．‎ ‎．‎ ‎，选（Ｄ）．‎ 点评：利用向量法求空间角，其操作只须按步骤进行，数值计算十分简单，对空间想象力和几何的逻辑推理能力要求不高，显得简洁明了．‎ ‎（3）利用空间向量求面面角 注意：求面面角的问题关键还是转化成求线线角，一般来说求二面角有两种方法：‎ 如图4，分别在二面角的两个面内且垂直于棱， ‎ 分别是的一个法向量，则可利用向量的夹角公式结合 以下角度关系之一求二面角的大小：‎ 方法一：等于二面角的平面角；‎ 方法二：与二面角的平面角相等或互补．‎ ‎（05云南一模）如图5，在三棱锥中，是边长为4的正三角形，平面平面，，分别为的中点，求二面角的余弦值．‎ 解：取中点，连结．‎ ‎，‎ ‎，且．‎ 又平面平面，‎ 平面，．‎ 如图5所示，建立空间直角坐标系．‎ 则，‎ ‎，，设为平面的一个法向量，则 ‎ 取，则 则．‎ 又为平面的一个法向量， ．‎ 二面角的余弦值为．‎ 点评：利用向量法求空间角的大小，经常用到平面的法向量．求法向量的方法主要有两种：‎ ‎① 求平面的垂线的方向向量；‎ ‎② 利用法向量与平面内两个不共线向量数量积为零列方程组求．‎ ‎4．用空间向量解决立体几何问题的“三步曲”‎ ‎（1）建立立体图形与空间向量的联系，用空间向量（或坐标）表示问题中涉及的点、线、面，从而把立体几何问题转化为向量问题（几何问题向量化）；‎ ‎（2）通过向量运算，研究点、线、面之间的位置关系以及它们之间的距离和夹角等问题（进行向量运算）；‎ ‎（3）把向量的运算结果“翻译”成相应的几何意义（回归几何问题）．‎ 四、易错点分析 ‎1．类比平面向量，是掌握空间向量的最好方法，平面向量的加、减、数乘等坐标运算公式及运算律对空间向量仍然成立．虽然共面向量定理由两个约束条件变为三个约束条件，坐标由两个有序实数推广到三个有序实数，但其运算规律实质上是一样的．例如线段的定比分点坐标公式（包括中点坐标公式、重心坐标公式）在空间直角坐标系中依然适用，有向线段表示向量的坐标仍然是终点减去始点坐标，平行、垂直的充要条件，夹角、距离公式等仍然适用．‎ ‎2．用向量知识证明立体几何问题，仍然离不开立体几何定理．如要证明线面平行，只需要证明平面外一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线∥，只需要证明（）即可．‎ ‎3．空间两条直线之间的夹角是不超过的角，因此，如果按照公式求出来的向量的数量积是一个负数，则应当取其绝对值，使之变为正值，这样求得的角为锐角．‎ ‎4．利用法向量求二面角时，要注意法向量的方向问题，结合二面角的大小，这样最后确定所求得的角到底是二面角还是二面角的补角． ‎ ‎5．在具体应用空间向量解决立体几何问题时要注意以下几点：‎ ‎（1）平行问题向量共线，注意重合 ‎（2）垂直问题向量的数量积为零，注意零向量 ‎（3）距离问题向量的模，注意向量的垂直 ‎（4）求角问题向量的夹角，注意角范围的统一 ‎6．解决立体几何问题的三种方法的比较 ‎　 解决立体几何中的问题，可用综合法、向量法和坐标法．一般我们遵循的原则是：以综合法为基础、以向量法为主导、以坐标法为中心．‎ ‎（1）综合法是以逻辑推理为工具，利用立体几何的知识，运用空间观念解决问题的方法，其显著特点是在证题时经常需要构造辅助线、辅助面、逻辑思维量大，要求具有比较强的空间想象能力．‎ ‎（2）向量法是根据空间向量的基本定理，运用向量的几何意义及向量数量积的概念解决立体几何的方法，是几何问题代数化的重要体现．其显著特点是可以避开纷繁复杂的逻辑推理，使解题过程变的明快、简捷．‎ ‎（3）坐标法是通过建立空间直角坐标系，设出点的坐标，利用向量的坐标运算来解决立体几何问题的方法．坐标法关键是在于构建合适的空间直角坐标系．‎ 注：构建空间直角坐标系主要有四种途径：‎ ‎① 利用共顶点的两两垂直的三条不共面的直线构建直角坐标系；‎ ‎② 利用线面垂直的位置关系构建直角坐标系；‎ ‎③ 利用面面垂直的位置关系构建直角坐标系；‎ ‎④ 利用正多边形的中心与几何体高所在直线构建直角坐标系．‎ 五、作者寄语 用向量研究立体几何问题是立体几何研究思路的一场革命．由于向量兼俱数和形的双重特征，使得立体图形中的位置关系转化为代数中的数量关系如同探囊取物，特别是据题目条件可以建立空间直角坐标系时，这种优越性便发挥的淋漓尽致，求解思路也将有效地避开立体几何中繁琐的位置关系的演化，而变得直截了当，变得清晰、自然和流畅．可以毫不客气地说：“只要建立了空间直角坐标系，剩下的便是纯属运算的问题了．”‎