- 2.21 MB
- 2021-05-14 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
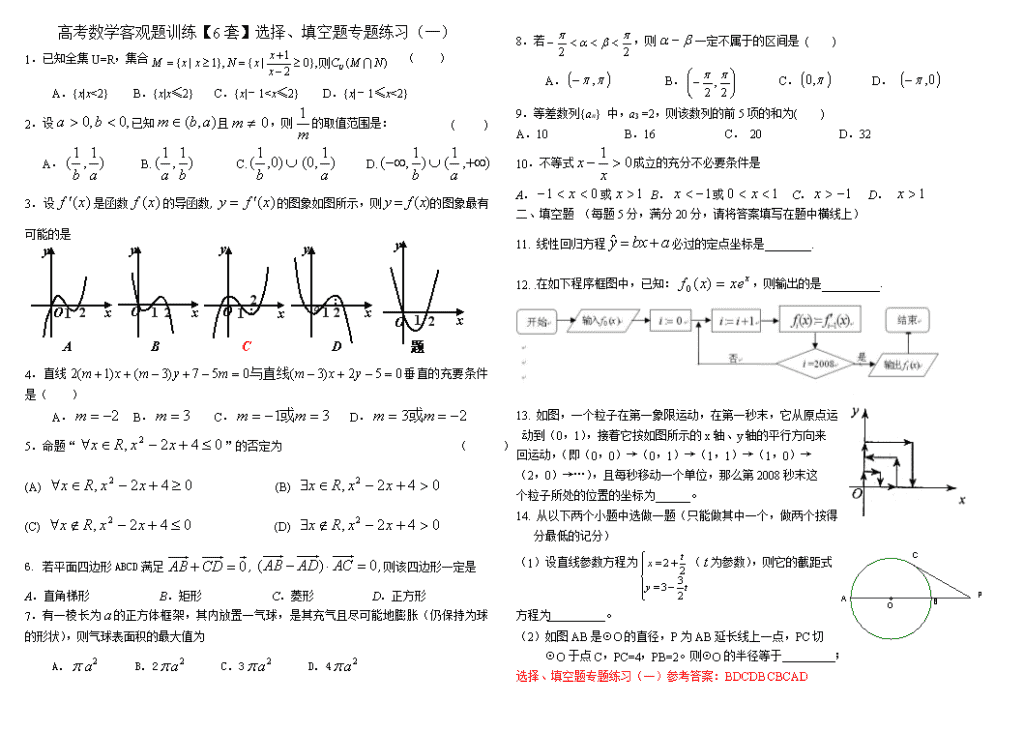
高考数学客观题训练【6套】选择、填空题专题练习(一)
1.已知全集U=R,集合 ( )
A.{x|x<2} B.{x|x≤2} C.{x|-1‖AB‖.其中真命题的个数为
A.0 B.1 C.2 D.3
O
M( , )
8.(上海卷)如图,平面中两条直线和相交于点O,对于平面上任意一点M,若、分别是M到直线和的距离,则称有序非负实数
对(,)是点M的“距离坐标”.已知常数≥0,
≥0,给出下列命题:
①若==0,则“距离坐标”为(0,0)的点有
且仅有1个;
②若=0,且+≠0,则“距离坐标”为(,)的点有且仅有2个;
③若≠0,则“距离坐标”为(,)的点有且仅有4个.
上述命题中,正确命题的个数是 ( )
(A)0; (B)1; (C)2; (D)3.
9.(07上海)某工程由四道工序组成,完成它们需用时间依次为天.四道工序的先后顺序及相互关系是:可以同时开工;完成后,可以开工;
完成后,可以开工.若该工程总时数为9天,则完成工序需要的天数最大是 .
10.(07福建)中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合中元素之间的一个关系“~”满足以下三个条件:
(1)自反性:对于任意,都有~;
(2)对称性:对于,若~,则有~;
(3)传递性:对于,若~,~,则有~.
则称“~”是集合的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出两个等价关系:______.
11.(四川卷)非空集合关于运算满足:(1)对任意、,都有;(2)存在,使得对一切,都有,则称关于运算为“融洽集”。现给出下列集合和运算:
①{非负整数},为整数的加法。 ②{偶数},为整数的乘法。
③{平面向量},为平面向量的加法。 ④{二次三项式},为多项式的加法。
⑤{虚数},为复数的乘法。
其中关于运算为“融洽集”的是 (写出所有“融洽集”的序号)
12.同学们都知道,在一次考试后,如果按顺序去掉一些高分,那么班级的平均分将降低;
反之,如果按顺序去掉一些低分,那么班级的平均分将提高. 这两个事实可以用数学语
言描述为:若有限数列 满足,则
(结论用数学式子表示).
二、课后训练:
1.集合P=1,3,5,7,9,┅,2-1,┅∈N,若∈P,∈P时,
∈P,则运算 可能是( )
(A)加法; (B)除法; (C)减法; (D)乘法.
2.定义一种运算“*”:对于自然数n满足以下运算性质:
(i)1*1=1,(ii)(n+1)*1=n*1+1,则n*1等于
A.n B.n+1 C.n -1 D.
x
1
2
3
g (f(x))
3.已知两个函数和的定义域和值域都是集合{1,2,3},其定义如下表.
填写下列的表格,其三个数依次为
x
1
2
3
f(x)
2
3
1
x
1
2
3
g(x)
1
3
2
A. 3,1,2 B . 2,1,3 C. 1,2,3 D. 3,2,1
4.在实数的原有运算法则中,我们补充定义新运算“”如下:
当时,; 当时,。
则函数的最大值等于( )
(“·”和“-”仍为通常的乘法和减法)
A. B. 1 C. 6 D. 12
5.定义运算 ,若复数,,则 。
6.有穷数列{an},Sn为其前n项和,定义为数列{an}的“凯森和”,
如果有99项的数列a1、a2、a3、…、a99的“凯森和”为1000,则有100项的数列
1、a1、a2、a3、a4、…a99的“凯森和”= 。
7.定义运算符号:“”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作,,其中ai为数列中的第i项.
①若,则T4= ;
②若 .
8.用类比推理的方法填表
等差数列中
等比数列中
9.在公差为的等差数列中,若是的前项和,则数列也成等差数列,且公差为,类比上述结论,相应地在公比为的等比数列中,若是数列的前项积,则有=______________ 。
10.考察下列一组不等式: 将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为
_________________________________
11.已知命题:平面上一矩形的对角线与边和
所成角分别为,则。若把它推广到空
间长方体中,试写出相应的命题形式:____________________
_____________________________________________________。
新定义型客观题训练
一、课堂训练:
1解析:由得,
所以,故选B.
2解:当x=0时,z=0,当x=1,y=2时,z=6,当x=1,y=3时,z=12,故所有元素之和为18,选D
3.解析:当接收方收到密文14,9,23,28时,
则,解得,解密得到的明文为C.
4.解析: A中1-2=-1不是自然数,即自然数集不满足条件;B中12=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中不是无理数,即无理数集不满足条件,故选择答案C。 5.C
6.解:依题意,有x1=50+x3-55=x3-5,x1
=
∴命题① ③成立,而命题②在中,若
则明显不成立,选B.
8.解:选(D) ① 正确,此点为点; ② 正确,注意到为常数,由中必有一个为零,另一个非零,从而可知有且仅有2个点,这两点在其中一条直线上,且到另一直线的距离为(或); ③ 正确,四个交点为与直线相距为的两条平行线和与直线相距为的两条平行线的交点; 9. 3
10.答案不唯一,如“图形的全等”、“图形的相似”、“非零向量的共线”、“命题的充要条件”.
11解析:非空集合关于运算满足:(1)对任意,都有;
(2)存在,使得对一切,都有,则称关于运算为“融洽集”;现给出下列集合和运算:
①,满足任意,都有,且令,有,所以①符合要求;
②,若存在,则,矛盾,∴ ②不符合要求;③,取,满足要求,∴ ③符合要求;
④,两个二次三项式相加得到的可能不是二次三项式,所以④不符合要求;
⑤,两个虚数相乘得到的可能是实数,∴ ⑤不符合要求,
这样关于运算为“融洽集”的有①③。
12.和
课后练习答案:
1.D 2答案:D 3答案:D 4.C 5答案:-4 6.991
7.105 ;8.答案:
9.
10.
11.长方体中,对角线与棱所成的角分别为,则,。或是:长方体中,对角线与平面所成的角分别为,则,。或是:长方体中,对角面与平面所成的二面角分别为,则。