高考数学广东卷答案详解理科 14页

‎2011年普通高等学校招生全国统一考试（广东卷）‎ 数学（理科）‎ 本试卷共4页，21小题，满分150分．考试用时120分钟．‎ 一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1． （（B） ‎ A． B． C． D． ‎ 解：(1+i）(1-i)=1-i2=1-(-1)=2。‎ 点评：本题是概念题，没有什么难度，属送分题。‎ ‎2． ，‎ ‎ （C）‎ A． B． C． D． ‎ 解：A为圆，圆心为(0,0),B为直线。显然直线B经过点(0,0)。即直线与圆相交。故选C。‎ 点评：只要理解集合的概念，及其所表示的点的轨迹，就会把问题变得简单。本题还可以用圆心到直线的距离来判断，但要是善于观察就会节省时间。也可以用联立方程来解，过程会相对复杂。‎ ‎3． （D）‎ A． B． C． D． ‎ 解：因为∥，⊥，所以⊥‎ 所以 点评：本题也是概念题没有难度。只要平时基础知识掌握到位，轻而易举。属送分题。‎ ‎4． （A） ‎ A． B． ‎ C． D． ‎ 解：设F(x)=f(x)+|g(x)|‎ 则F(-x)=f(-x)+|g(-x)|=f(x)+|-g(x)|=f(x)+|g(x)|=F(x)。故选A。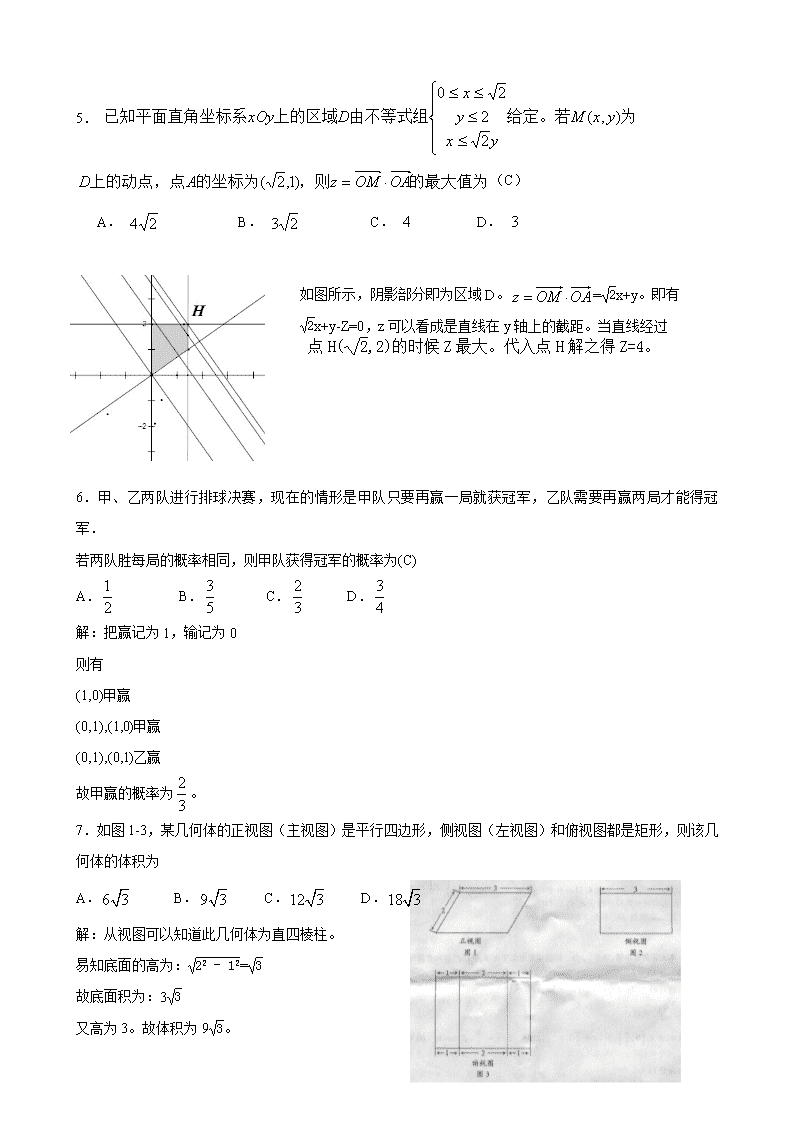‎ ‎5． ‎ ‎（C）‎ A． B． C． D． ‎ ‎ 如图所示，阴影部分即为区域D。=x+y。即有 ‎ x+y-Z=0，z可以看成是直线在y轴上的截距。当直线经过 ‎ 点H(,2)的时候Z最大。代入点H解之得Z=4。‎ ‎6．甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军．‎ 若两队胜每局的概率相同，则甲队获得冠军的概率为(C)‎ A． B． C． D．‎ 解：把赢记为1，输记为0‎ 则有 ‎(1,0)甲赢 ‎(0,1),(1,0)甲赢 ‎(0,1),(0,1)乙赢 故甲赢的概率为。‎ ‎7．如图1-3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为 A． B． C． D．‎ 解：从视图可以知道此几何体为直四棱柱。‎ 易知底面的高为：= 故底面积为：3 又高为3。故体积为9。‎ ‎8．设是整数集的非空子集，如果，有，则称关于数的乘法是封闭的．若是的两个不相交的非空子集, ,且,有；,有,则下列结论恒成立的是（A）‎ A． 中至少有一个关于乘法是封闭的 B． 中至多有一个关于乘法是封闭的 C． 中有且只有一个关于乘法是封闭的 D． 中每一个关于乘法都是封闭的 解：1)设T,V都不封闭。则，有abT,否则若ab∈T，cT,abcT。这与假设T不封闭矛盾。‎ 同理：bcT,acT。故abV,bcV, ,acV。ab·bc T,即abc·bT。这与T不封闭矛盾。‎ ‎ 2）若两个都封闭。则有,abT,abcT;同理，xyV,xyzV。所以T，V封闭时成立。‎ ‎ 3）设一个不封闭，一个封闭。不妨设T不封闭。则有,有abV, bcV,则有ab·bcV 即abc·bV。此时也成立。‎ ‎ 故至少有一个是关于乘法是封闭的。‎ 二、填空题：本大题共7小题．考生作答6小题．每小题5分，满分30分． ‎ ‎（一）必做题（9～13题）‎ ‎9．不等式的解集是[1,+∞)‎ 解：由原式化为 ‎|x+1|≥|x-3|‎ ‎(x+1)2≥(x-3)2‎ x2+2x+1≥x2-6x+9‎ ‎8x≥8‎ x≥1‎ ‎10．的展开式中的系数是 84 （用数字作答）．‎ 解：原式=,的项，即为(x-2x-1)7的展开式中x3的项。其展开式项为：。当7-2m=3时，解得m=2。则系数为：‎ ‎11．等差数列的前9项和等于前4项和，若，则 10 ．‎ 解：(a1+a2+……a9)-(a1+a2+a3+a4)=a5+a6+a7+a8+a9=5a7=0,所以：a7=0,ak+a4=2a7,所以k=10‎ ‎12．函数在 2 处取得极小值．‎ 解：=3x(x-2)=0,解得x1=0，x2=2.‎ 如图所示，x<0，>0;‎ ‎02，>0‎ 所以，在x=2时取得极小值。‎ ‎13．某数学老师身高176cm，他爷爷，父亲，儿子的身高分别是173cm,170cm和182cm，因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高是185 cm．‎ 解：‎ x ‎173‎ ‎170‎ ‎176‎ ‎182‎ y ‎170‎ ‎176‎ ‎182‎ ‎?‎ 设y=bx+a y=x+3‎ y4=182+3=185‎ ‎（二）选做题（14、15题，考生只能从中选做一题）‎ ‎14．（坐标系与参数方程选做题）已知两曲线参数方程分别为（0≤q ＜p ＝和 ‎（t∈R），它们的交点坐标为(1, )．‎ 解：由第一组方程知y≥0,由第二组方程组知x≥0.‎ 化为直角坐标系下的方程则有：‎ ‎………… y2=………………………………………… 联立,且x≥0，y≥0解得x=1，y=‎ ‎15．（几何证明选讲选做题）如图4，过圆外一点P分别做圆的切线和割线交圆于A,B两点，且PB=7，C是圆上一点使得BC=5，则AB= ．‎ 解：∠PAB=∠ACB（弦切角定理）‎ 又所以△PAB∽△ACB 所以AB:PB=BC:AB AB2=PB·BC=35‎ AB= 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．‎ ‎16．（本小题满分12分）‎ 已知函数．‎ ‎（1）求的值；‎ ‎（2）设，，，求的值．‎ 解：（1）=。‎ ‎（2）‎ 点评：本题考考察了三角函数的基本公式。没有难度，属送分题。‎ ‎17．（本小题满分13分）‎ 为了解甲，乙两厂的产品质量，采取分层抽样的方法从甲，乙两厂的产品中分别抽取14件和5件，测量产品中微量元素的含量（单位：毫克）．下表是乙厂的5件产品的测量数据：‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎169‎ ‎178‎ ‎166‎ ‎175‎ ‎180‎ ‎75‎ ‎80‎ ‎77‎ ‎70‎ ‎81‎ （1） 已知甲厂生产的产品共有98件，求乙厂生产的产品数量；‎ （2） 当产品中微量元素满足且时，该产品为优等品．用上述样本数据估计乙厂生产的优等品的数量；‎ （3） 从乙厂抽出的上述5件产品中，随机抽取2件，求抽出的2件产品中优等品数的分布列及其均值（即数学期望）．‎ 解：（1）设乙厂的产品有m个，依题意98:14=m:5，解得：m=35。即乙厂的产品数为35个。‎ ‎（2）从表中可以5件产品中只有第2和第5个产品满足且。‎ ‎ 故优等产品的概率P=2/5=0.4。‎ ‎ 故乙厂的优等品的数量：35×0.4=14（个）‎ ‎（3）随机抽二件，出现优等品数可能为0,1,2。5件产品中取2件的取法有：‎ P(=0)=；P(=1)= ；P(=2)= ‎ 其分布列为：‎ ‎0‎ ‎1‎ ‎2‎ P 均值：E()=0×+1×+2×=1.4‎ ‎18．（本小题满分13分）‎ 如图5，在锥体P-ABCD中，ABCD是边长为1的菱形，且，，PB=2，E，F分别是BC，PC的中点．‎ (1) 证明：AD⊥平面DEF；‎ (1) 求二面角P-AD-B的平面角的余弦值。‎ ‎（1）证明：如图取AD的中点H，连结PH,BH。‎ ‎∵PA=PD，∴PH⊥AD…………………………… ‎∵ABCD是边长为1的菱形，且 ‎∴AB=BD ‎∴BH⊥AD…………………………………………… ‎∴由得AD⊥面PBH…………………………… ‎∴AD⊥PB………………………………………… 又E，F是BC,PC的中点 ‎∴EF∥PB………………………………………… 由得 AD⊥EF………………………………………… 又E是BC的中点，DC=DB ‎∴DE⊥BC ,AC∥BC ‎∴AD⊥DE……………………………………… 由得 AD⊥面DEF 证毕。‎ ‎（2）解：∵PH⊥AD，BH⊥AD ‎∴二面角P-AD-B的平面角为∠PHB，设为角H 则有PB2=PH2+BH2-2PH·BH·cosH PB=2‎ PH==‎ BH==‎ 代入解得：cosH=‎ 即二面角P-AD-B的平面角的余弦值为。‎ ‎19．（本小题满分14分）‎ 设圆C与两圆，中的一个内切，另一个外切．‎ （1） 求C的圆心轨迹L的方程；‎ （2） 已知点M（，），F（，0），且P为L上的动点，求的最大值及此时点P的坐标．‎ 解：(1)设圆C的半径为r，圆心为K(x,y)，‎ 圆心H(-,0), ‎ 圆心为T(,0)‎ 则依题意有|KH|=r+2,|KT|=r-2; 或|KH|=r-2, |KT|=r+2。从而||KH|-|KT||=4。‎ 即到两定之间的距离之差为常数。即L的轨迹为双曲线。‎ 设 c2=5‎ a=2,所以a2=4。‎ b2=c2-a2=5-4=1‎ 即L的轨迹方程为：‎ ‎(2)‎ 如图所示：连结MF，且延长MF交双曲线于点F的另则的点P。则此时=|MF|值最大。‎ 因为，如若不然，在其它，如点P’，则根据三角形的性质则<|MF|。‎ ‎|MF|=。即|的最大值为2。‎ 过M，P两点的直线方程为：‎ 化简得：‎ 联立方程： ‎ ‎ ‎ 解得：‎ ‎ ‎ ‎ ‎ 即取得最大值时的P的坐标为(,)。 ‎ ‎20．（本小题满分14分）‎ ‎ 设b>0,数列满足,．‎ （1） 求数列的通项公式；‎ （2） 证明：对于一切正整数,．‎ ‎（1）解：‎ ‎∵，a1=b>0。∴an>0‎ 整理得 设cn=,则有：cn=‎ 设cn+t=‎ ‎ 即cn=‎ ‎ 令。解得t=‎ 设dn=cn+‎ 即{dn}以公比为的等比数列。d1=C1+=‎ 所以dn=‎ 所以an=‎ ‎ (2)证明： ‎ ‎ ‎ 以上式式相加，并整理可得：‎ 证毕。‎ ‎21．（本小题满分14分）‎ 在平面直角坐标系上，给定抛物线，实数满足，是方程的两根，记．‎ （1） 过点作L的切线交轴于点B．证明：对线段AB上的任一点，有；‎ （2） 设是定点，其中满足．过作L的两条切线，切点分别为，‎ 与轴分别交于．线段EF上异于两端点的点集记为X，‎ 证明：；‎ （1） 设，当点取遍D时，求的最小值（记为）和最大值（记为）．‎ ‎（1）证明：对抛物线L的方程求导： 。又点在抛物线上。故过点A的切线斜率为：P0。‎ 即此切线方程为：。‎ 则其与y轴的交点坐标为(0,)。‎ 对AB上的任一点，‎ ‎1）若p0<0，则p00，则00，即0由（1）知过点(,)，和点(,)L的方程分别为 l1：‎ l2：‎ 又点M(a,b)是两条切线的交点。‎ 于是有 ‎ ‎ ‎ ‎ ‎ ‎ 整理得：‎ ‎ ‎ ‎ 又因为4a2-4b>0。‎ ‎ 所以，p1,p2是一元二次方程x2-2ax+4b=0的两根。‎ 解得x1,2=‎ 若p1<0，则直线的斜率，又M(a,b)∈X 所以p1||‎ 若p1>0，则直线的斜率，又M(a,b)∈X 所以0||‎ 综上所述，若M(a,b)∈X||>||‎ ‎<二>若||>||‎ 若a<0，则，故有p10，则，故有0||M(a,b)∈X 综合<一>、<二>得 M(a,b)∈X||>||‎ ‎<三>由<一>易知 ‎,即 ‎,是方程：x2-ax+b=0的两实根。‎ 又知M(a,b)∈X||>||。‎ 证毕。‎ ‎（3）由解得0| p- 所以 q≥‎ 化简整理得p2-4q≤4-2p 即m1= p+≤p+ 设t=,在为0≤p≤2,所以0≤t≤2‎ 则m1=p+化为m1=-+t+2=‎ 当t=1时，m1=，此时m1最大。‎ 当t=0时，m1=2，此时m1最小。‎ 即 ‎ ‎ QQ:2816878. 水平有限，有宝贵意见欢迎指点。‎ 博客：http://blog.sina.com.cn/kukialee