2006-2013广东高考文科数学立体几何大题 7页

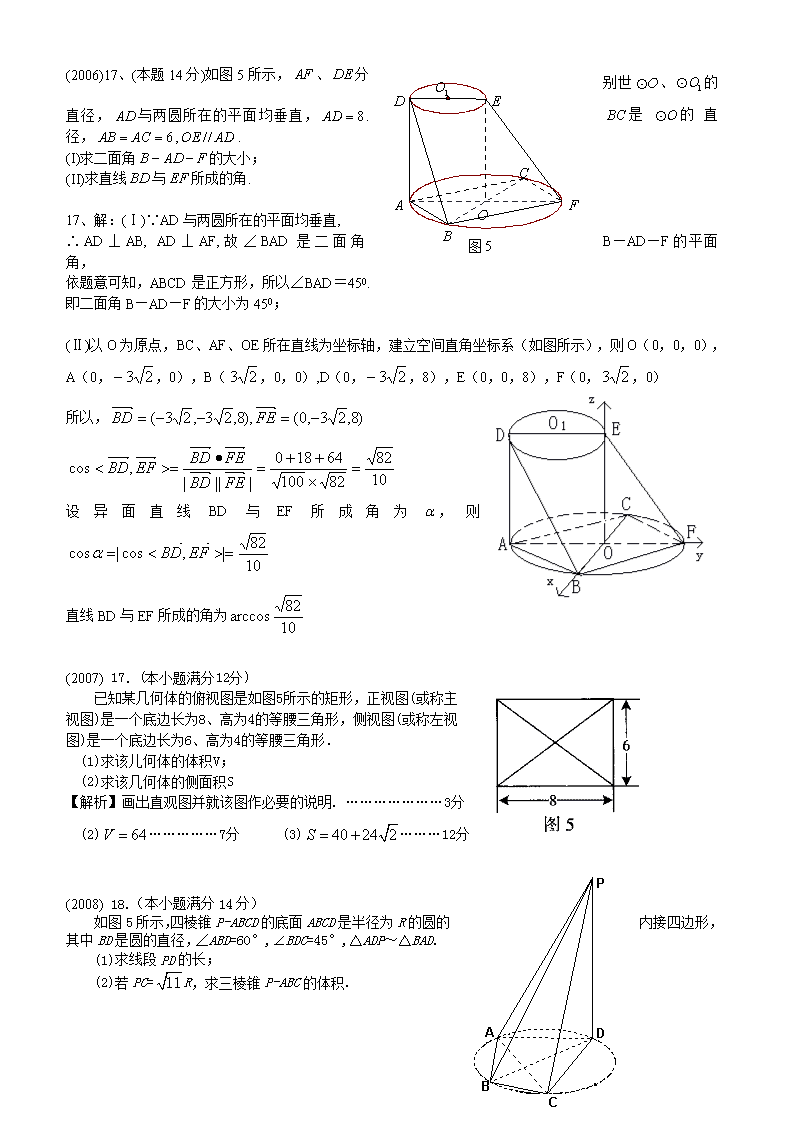
图5‎ ‎(2006)17、(本题14分)如图5所示，、分别世、的直径，与两圆所在的平面均垂直，.是的直径，,.‎ ‎(I)求二面角的大小；‎ ‎(II)求直线与所成的角.‎ ‎17、解：(Ⅰ)∵AD与两圆所在的平面均垂直,‎ ‎∴AD⊥AB, AD⊥AF,故∠BAD是二面角B—AD—F的平面角，‎ 依题意可知，ABCD是正方形，所以∠BAD＝450.‎ 即二面角B—AD—F的大小为450；‎ ‎(Ⅱ)以O为原点，BC、AF、OE所在直线为坐标轴，建立空间直角坐标系（如图所示），则O（0，0，0），A（0，，0），B（，0，0）,D（0，，8），E（0，0，8），F（0，，0）‎ 所以，‎ 设异面直线BD与EF所成角为，则 直线BD与EF所成的角为 ‎(2007) 17．(本小题满分12分)‎ ‎ 已知某几何体的俯视图是如图5所示的矩形，正视图(或称主 视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视 图)是一个底边长为6、高为4的等腰三角形．‎ ‎ (1)求该儿何体的体积V；‎ ‎ (2)求该几何体的侧面积S ‎【解析】画出直观图并就该图作必要的说明. …………………3分 ‎ (2)……………7分 (3)………12分 ‎(2008) 18.（本小题满分14分）‎ 如图5所示，四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径，∠ABD=60°,∠BDC=45°,△ADP～△BAD.‎ ‎(1)求线段PD的长；‎ ‎(2)若PC=R，求三棱锥P-ABC的体积.‎ ‎ 图5‎ ‎18．解：（1）因为是园的直径，所以 ‎ 又△ADP～△BAD.‎ ‎ 所以 ‎ ‎ （2）在中，‎ ‎ 因为 ‎ ‎ 所以 又 ‎ 所以底面 ‎ ‎ ‎ 三棱锥体积为 ‎(2009) 17.（本小题满分13分）‎ 某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.‎ ‎（1）请画出该安全标识墩的侧(左)视图 ‎（2）求该安全标识墩的体积 ‎（3）证明:直线BD平面PEG ‎【解析】(1)侧视图同正视图,如下图所示.‎ ‎　　　（２）该安全标识墩的体积为：‎ ‎　　　　　　　　‎ ‎　　　（３）如图,连结EG,HF及 BD，EG与HF相交于O,连结PO.‎ ‎ 由正四棱锥的性质可知,平面EFGH , ‎ ‎ 又 平面PEG ‎ 又 平面PEG；‎ ‎(2010) 18.(本小题满分14分) w_w w. k#s5_u.c o*m 如图4，是半径为的半圆，为直径，点为弧AC的中点，点和点为线段的三等分点，平面外一点满足平面，=. ‎ ‎（1）证明：；‎ ‎（2）求点到平面的距离. w_w*w.k_s_5 u.c*o*m ‎18．法一：（1）证明：∵点B和点C为线段AD的三等分点， ∴点B为圆的圆心 又∵E是弧AC的中点，AC为直径， ∴即 ‎ ∵平面，平面， ∴‎ ‎ 又平面，平面且 ∴平面 ‎ 又∵平面， ∴‎ ‎（2）解：设点B到平面的距离（即三棱锥的高）为.‎ ‎ ∵平面, ∴FC是三棱锥F-BDE的高，且三角形FBC为直角三角形 ‎ 由已知可得，又 ∴‎ ‎ 在中，，故,‎ ‎ ∴,‎ ‎ 又∵平面，故三角形EFB和三角形BDE为直角三角形,‎ ‎ ∴，在中，, ∴,‎ ‎ ∵即，故,‎ 即点B到平面的距离为.‎ ‎ 法二：向量法，此处略，请同学们动手完成。‎ ‎(2011)18．（本小题满分13分）‎ ‎ 图5所示的集合体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的．A，A′，B，B′分别为,,,的中点，分别为的中点．‎ ‎（1）证明：四点共面；‎ ‎（2）设G为A A′中点，延长到H′，使得．证明：‎ ‎18．（本小题满分13分）‎ ‎ 证明：（1）中点，‎ ‎ ‎ ‎ 连接BO2‎ ‎ 直线BO2是由直线AO1平移得到 ‎ ‎ ‎ ‎ ‎ 共面。‎ ‎ （2）将AO1延长至H使得O1H=O‎1A，连接 ‎//‎ ‎ 由平移性质得=HB ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎2012年18.（本小题满分13分）‎ 如图5所示，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD，PD=AD，E是PB的中点，F是DC上的点且DF=AB，PH为△PAD边上的高。‎ （1） 证明：PH⊥平面ABCD；‎ （2） 若PH=1，AD=，FC=1，求三棱锥E-BCF的体积；‎ （1） 证明：EF⊥平面PAB。*‎ ‎【解析】(1)证明:因为PH为△PAD边上的高,所以PH⊥AD,又因为AB⊥平面PAD，平面PAD,所以AB⊥PH,又因为PHAD=H,所以PH⊥平面ABCD;‎ ‎(2)因为E是PB的中点，所以点E到平面BCF的距离等于点P到平面ABCD距离的一半,即=,又因为=,所以三棱锥E-BCF的体积为;‎ ‎2013年18．（本小题满分13分）‎ 如图4，在边长为1的等边三角形中，分别是边上的点，，是的中点，与交于点，将沿折起，得到如图5所示的三棱锥，其中．‎ ‎(1) 证明：//平面；‎ ‎(2) 证明：平面；‎ ‎(3) 当时，求三棱锥的体积．‎ ‎18. 解：（1）在等边三角形中， ‎ ‎,在折叠后的三棱锥中也成立，‎ ‎ ,平面，‎ 平面，平面；‎ ‎（2）在等边三角形中，是的中点，所以①，.‎ ‎ 在三棱锥中，，②‎ ‎；‎ ‎（3）由（1）可知，结合（2）可得.‎