高考数学总复习定积分和微积分基本定理 5页

第三节定积分和微积分基本定理 考纲解读 ‎1.了解定积分的实际背景、基本思想及概念.‎ ‎2.了解微积分基本定理的含义.‎ 命题趋势探究 定积分的考查以计算为主，其应用主要是求一个曲边梯形的面积，题型主要为选择题和填空题.‎ 知识点精讲 一、基本概念 ‎1.定积分的极念 一般地，设函效在区间[a，b]上连续.用分点 将区间等分成个小区间，每个小区间长度为（），在每个小区间上任取一点，作和式： ，当无限接近于（亦即）时，上述和式无限趋近于常数，那么称该常数为函数在区间上的定积分．记为：，为被积函数，为积分变量，为积分区间，为积分上限，为积分下限．‎ 需要注意以下几点：‎ ‎（1）定积分是一个常数，即无限趋近的常数（时），称为，而不是．‎ ‎（2）用定义求定积分的一般方法.‎ ‎①分割：等分区间；②近似代替：取点；③求和：；④取极限：‎ ‎（3）曲边图形面积：；变速运动路程；变力做功 ‎2．定积分的几何意义 从几何上看，如果在区间上函数连续且恒有，那么定积分表示由直线和曲线所围成的曲边梯形(如图3-13中的阴影部分所示)的面积，这就是定积分的几何意义．‎ 一般情况下，定积分的值的几何意义是介于轴、函数的图像以及直线之间各部分面积的代数和，在轴上方的面积取正号，在轴下方的面积取负号．‎ 二、基本性质 性质1 .‎ 性质2 （定积分的线性性质）.‎ 性质3 （定积分的线性性质）.‎ 性质4 （定积分对积分区间的可加性）‎ 推广1 ‎ 推广2 ．‎ 三、基本定理 设函数是在区间上连续，且是是在上的任意一个原函数，即，则，或记为 ，称为牛顿—莱布尼兹公式，也称为微积分基本定理．‎ 该公式把计算定积分归结为求原函数的问题，只要求出被积函数的一个原函数．然后计算原函数在区间上的增量即可，这一定理提示了定积分与不定积分之间的内在联系．‎ 题型归纳及思路提示 题型51 定积分的计算 思路提示 对于定积分的计算问题，若该定积分具有明显的几何意义，如圆的面积等（例3.26及其变式），则利用圆面积计算，否则考虑用牛顿-莱布尼茨公式计算．‎ 例3.25（2012江西11）计算= ．‎ 解析 ．‎ A. B. C. D. ‎ 变式1 ‎ A. B. C. D. ‎ 变式2 ‎ A.1 B. C. D. ‎ 变式3 设函数，若，则的值为 ．‎ 变式4 设函数的定义域为R, 若对于给定的正数，定义函数 ‎，则当函数时，定积分的值为 ‎（ ）‎ A. B. C. D. 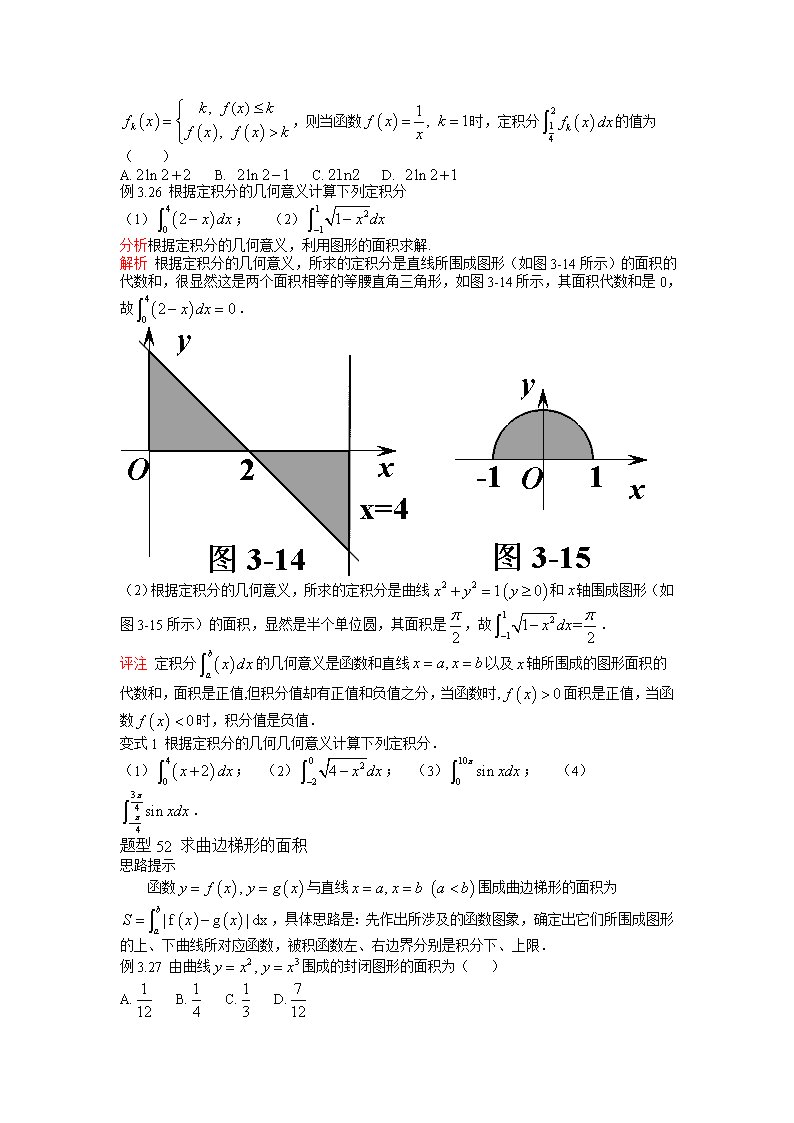‎ 例3.26 根据定积分的几何意义计算下列定积分 ‎（1）； （2）‎ 分析根据定积分的几何意义，利用图形的面积求解.‎ 解析 根据定积分的几何意义，所求的定积分是直线所围成图形（如图3-14所示）的面积的代数和，很显然这是两个面积相等的等腰直角三角形，如图3-14所示，其面积代数和是0，故．‎ ‎（2）根据定积分的几何意义，所求的定积分是曲线和轴围成图形（如图3-15所示）的面积，显然是半个单位圆，其面积是，故．‎ 评注 定积分的几何意义是函数和直线以及轴所围成的图形面积的代数和，面积是正值,但积分值却有正值和负值之分，当函数时,面积是正值，当函数时，积分值是负值．‎ 变式1 根据定积分的几何几何意义计算下列定积分．‎ ‎（1）； （2）； （3）； （4）．‎ 题型52 求曲边梯形的面积 思路提示 函数与直线围成曲边梯形的面积为，具体思路是：先作出所涉及的函数图象，确定出它们所围成图形的上、下曲线所对应函数，被积函数左、右边界分别是积分下、上限．‎ 例3.27 由曲线围成的封闭图形的面积为（ ）‎ A. B. C. D.‎ 解析 由得则由和围成的封闭图形的面积为，故选A．‎ 变式1（2012湖北理3）已知二次函数的图象如图3-16所求，则它与轴所围成图形的面积为（ ）‎ A. B. C. D.‎ y x O 图3-16‎ 变式2 由曲线和直线所围成的图形（如图3-17中阴影部分所示）面积的最小值为（ ）‎ A. B. C. D.‎ 变式3 求抛物线与围成的平面图形的面积．‎ 变式4 求由两条曲线和直线所围成的面积．‎ 最有效训练题16（限时45分钟）‎ ‎1.已知函数，则（ ）‎ A. -2 B. C.-4 D. ‎ ‎2.定积分（ ）‎ A, B. C. D. ‎ ‎3.设，则（ ）‎ A. B. C. D.不存在 ‎ ‎4.，则的大小关系是（ ）‎ A, B. C. D. ‎ ‎5.曲线与直线所围成的平面区域的面积为（ ）‎ A,１ B. ‎２ C. D. ‎ ‎6.由直线与曲线所围成的平面图形的面积为（ ）‎ A, B‎.１ C. D. ‎ ‎7.抛物线与直线围成的平面图形的面积为　　　　　　．‎ ‎8.已知是偶函数，且，则　　　　　　．‎ ‎9. 　　　　　　．‎ ‎10.已知函数的图象是折线段ABC，其中．函数的图象与轴所围成的图形的面积为　　　　　　．‎ ‎11.根据定积分的几何意义计算下列定积分．‎ ‎（１）；　　（２）；　　（３）；　‎ ‎（４）；　　（５）‎ ‎１２．有一条直线与抛物线相交于Ａ，Ｂ两点，线段ＡＢ与抛物线所围成图形的面积恒等于，求线段ＡＢ的中点Ｐ的轨迹方程．‎