高考数学真题汇编数列有答案 42页

高考数学真题汇编---数列 学校：___________姓名：___________班级：___________考号：___________‎ ‎　一．选择题（共9小题）‎ ‎1．（2017•新课标Ⅰ）记Sn为等差数列{an}的前n项和．若a4+a5=24，S6=48，则{an}的公差为（　　）‎ A．1 B．2 C．4 D．8‎ ‎2．（2017•新课标Ⅱ）在明朝程大位《算法统宗》中有这样的一首歌谣：“远看巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”这首古诗描述的这个宝塔（古称浮屠），本题说它一共有7层，每层悬挂的红灯数是上一层的2倍，共有381盏灯，问塔顶有几盏灯？你算出的结果是（　　）‎ A．6 B．5 C．4 D．3‎ ‎3．（2017•新课标Ⅲ）等差数列{an}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{an}前6项的和为（　　）‎ A．﹣24 B．﹣3 C．3 D．8‎ ‎4．（2017•新课标Ⅰ）几位大学生响应国家的创业号召，开发了一款应用软件．为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动．这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推．求满足如下条件的最小整数N：N＞100且该数列的前N项和为2的整数幂．那么该款软件的激活码是（　　）‎ A．440 B．330 C．220 D．110‎ ‎5．（2016•上海）已知无穷等比数列{an}的公比为q，前n项和为Sn，且=S，下列条件中，使得2Sn＜S（n∈N*）恒成立的是（　　）‎ A．a1＞0，0.6＜q＜0.7 B．a1＜0，﹣0.7＜q＜﹣0.6‎ C．a1＞0，0.7＜q＜0.8 D．a1＜0，﹣0.8＜q＜﹣0.7‎ ‎6．（2016•新课标Ⅰ）已知等差数列{an}前9项的和为27，a10=8，则a100=（　　）‎ A．100 B．99 C．98 D．97‎ ‎7．（2016•四川）某公司为激励创新，计划逐年加大研发资金投入．若该公司2015年全年投入研发资金130万元，在此基础上，每年投入的研发资金比上一年增长12%，则该公司全年投入的研发资金开始超过200万元的年份是（　　）‎ ‎（参考数据：lg1.12=0.05，lg1.3=0.11，lg2=0.30）‎ A．2018年 B．2019年 C．2020年 D．2021年 ‎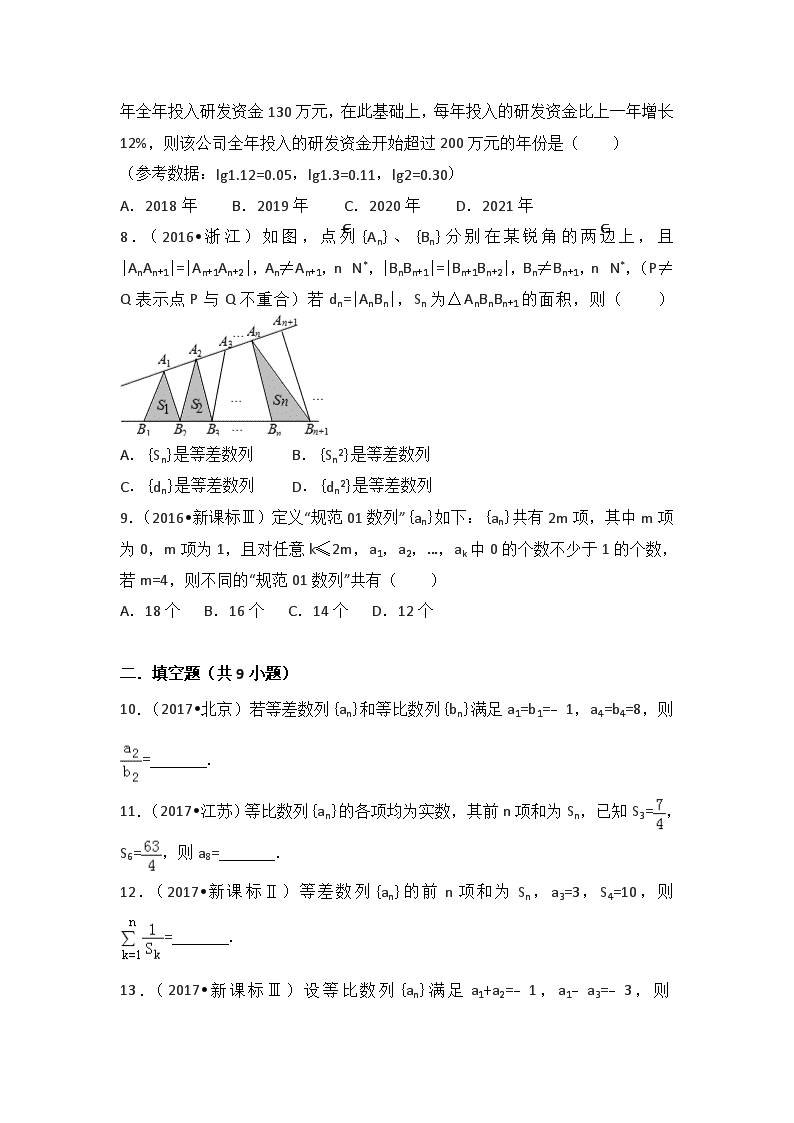8．（2016•浙江）如图，点列{An}、{Bn}分别在某锐角的两边上，且|AnAn+1|=|An+1An+2|，An≠An+1，n∈N*，|BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+1，n∈N*，（P≠Q表示点P与Q不重合）若dn=|AnBn|，Sn为△AnBnBn+1的面积，则（　　）‎ A．{Sn}是等差数列 B．{Sn2}是等差数列 C．{dn}是等差数列 D．{dn2}是等差数列 ‎9．（2016•新课标Ⅲ）定义“规范01数列”{an}如下：{an}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a1，a2，…，ak中0的个数不少于1的个数，若m=4，则不同的“规范01数列”共有（　　）‎ A．18个 B．16个 C．14个 D．12个 ‎　‎ 二．填空题（共9小题）‎ ‎10．（2017•北京）若等差数列{an}和等比数列{bn}满足a1=b1=﹣1，a4=b4=8，则=　 　．‎ ‎11．（2017•江苏）等比数列{an}的各项均为实数，其前n项和为Sn，已知S3=，S6=，则a8=　 　．‎ ‎12．（2017•新课标Ⅱ）等差数列{an}的前n项和为Sn，a3=3，S4=10，则 =　 　．‎ ‎13．（2017•新课标Ⅲ）设等比数列{an}满足a1+a2=﹣1，a1﹣a3‎ ‎=﹣3，则a4=　 　．‎ ‎14．（2016•江苏）已知{an}是等差数列，Sn是其前n项和，若a1+a22=﹣3，S5=10，则a9的值是　 　．‎ ‎15．（2016•北京）已知{an}为等差数列，Sn为其前n项和．若a1=6，a3+a5=0，则S6=　 　．‎ ‎16．（2016•上海）无穷数列{an}由k个不同的数组成，Sn为{an}的前n项和，若对任意n∈N*，Sn∈{2，3}，则k的最大值为　 　．‎ ‎17．（2016•新课标Ⅰ）设等比数列{an}满足a1+a3=10，a2+a4=5，则a1a2…an的最大值为　 　．‎ ‎18．（2016•浙江）设数列{an}的前n项和为Sn，若S2=4，an+1=2Sn+1，n∈N*，则a1=　 　，S5=　 　．‎ ‎　三．解答题（共22小题）‎ ‎19．（2017•新课标Ⅱ）已知等差数列{an}的前n项和为Sn，等比数列{bn}的前n项和为Tn，a1=﹣1，b1=1，a2+b2=2．‎ ‎（1）若a3+b3=5，求{bn}的通项公式；‎ ‎（2）若T3=21，求S3．‎ ‎20．（2017•山东）已知{xn}是各项均为正数的等比数列，且x1+x2=3，x3﹣x2=2．‎ ‎（Ⅰ）求数列{xn}的通项公式；‎ ‎（Ⅱ）如图，在平面直角坐标系xOy中，依次连接点P1（x1，1），P2（x2，2）…Pn+1（xn+1，n+1）得到折线P1 P2…Pn+1，求由该折线与直线y=0，x=x1，x=xn+1所围成的区域的面积Tn．‎ ‎21．（2017•山东）已知{an}是各项均为正数的等比数列，且a1+a2=6，a1a2=a3．‎ ‎（1）求数列{an}通项公式；‎ ‎（2）{bn} 为各项非零的等差数列，其前n项和为Sn，已知S2n+1=bnbn+1，求数列的前n项和Tn．‎ ‎22．（2017•天津）已知{an}为等差数列，前n项和为Sn（n∈N*），{bn}是首项为2的等比数列，且公比大于0，b2+b3=12，b3=a4﹣2a1，S11=11b4．‎ ‎（Ⅰ）求{an}和{bn}的通项公式；‎ ‎（Ⅱ）求数列{a2nbn}的前n项和（n∈N*）．‎ ‎23．（2017•天津）已知{an}为等差数列，前n项和为Sn（n∈N+），{bn}是首项为2的等比数列，且公比大于0，b2+b3=12，b3=a4﹣2a1，S11=11b4．‎ ‎（Ⅰ）求{an}和{bn}的通项公式；‎ ‎（Ⅱ）求数列{a2nb2n﹣1}的前n项和（n∈N+）．‎ ‎24．（2017•新课标Ⅲ）设数列{an}满足a1+3a2+…+（2n﹣1）an=2n．‎ ‎（1）求{an}的通项公式；‎ ‎（2）求数列{}的前n项和．‎ ‎25．（2017•新课标Ⅰ）记Sn为等比数列{an}的前n项和．已知S2=2，S3=﹣6．‎ ‎（1）求{an}的通项公式；‎ ‎（2）求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列．‎ ‎26．（2017•江苏）对于给定的正整数k，若数列{an}满足：an﹣k+an﹣k+1+…+an﹣1+an+1+…+an+k﹣1+an+k=2kan对任意正整数n（n＞k）总成立，则称数列{an}是“P（k）数列”．‎ ‎（1）证明：等差数列{an}是“P（3）数列”；‎ ‎（2）若数列{an}既是“P（2）数列”，又是“P（3）数列”，证明：{an}是等差数列．‎ ‎27．（2017•北京）已知等差数列{an}和等比数列{bn}满足a1=b1=1，a2+a4=10，b2b4=a5．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）求和：b1+b3+b5+…+b2n﹣1．‎ ‎28．（2017•北京）设{an}和{bn}是两个等差数列，记cn=max{b1﹣a1n，b2﹣a2n，…，bn﹣ann}（n=1，2，3，…），其中max{x1，x2，…，xs}表示x1，x2，…，xs这s个数中最大的数．‎ ‎（1）若an=n，bn=2n﹣1，求c1，c2，c3的值，并证明{cn}是等差数列；‎ ‎（2）证明：或者对任意正数M，存在正整数m，当n≥m时，＞M；或者存在正整数m，使得cm，cm+1，cm+2，…是等差数列．‎ ‎29．（2017•浙江）已知数列{xn}满足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*），证明：当n∈N*时，‎ ‎（Ⅰ）0＜xn+1＜xn；‎ ‎（Ⅱ）2xn+1﹣xn≤；‎ ‎（Ⅲ）≤xn≤．‎ ‎30．（2016•北京）已知{an}是等差数列，{bn}是等比数列，且b2=3，b3=9，a1=b1，a14=b4．‎ ‎（1）求{an}的通项公式；‎ ‎（2）设cn=an+bn，求数列{cn}的前n项和．‎ ‎31．（2016•北京）设数列A：a1，a2，…，aN （N≥2）．如果对小于n（2≤n≤‎ N）的每个正整数k都有ak＜an，则称n是数列A的一个“G时刻”，记G（A）是数列A的所有“G时刻”组成的集合．‎ ‎（Ⅰ）对数列A：﹣2，2，﹣1，1，3，写出G（A）的所有元素；‎ ‎（Ⅱ）证明：若数列A中存在an使得an＞a1，则G（A）≠∅；‎ ‎（Ⅲ）证明：若数列A满足an﹣an﹣1≤1（n=2，3，…，N），则G（A）的元素个数不小于aN﹣a1．‎ ‎32．（2016•新课标Ⅱ）等差数列{an}中，a3+a4=4，a5+a7=6．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）设bn=[an]，求数列{bn}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2．‎ ‎33．（2016•天津）已知{an}是等比数列，前n项和为Sn（n∈N*），且﹣=，S6=63．‎ ‎（1）求{an}的通项公式；‎ ‎（2）若对任意的n∈N*，bn是log2an和log2an+1的等差中项，求数列{（﹣1）nb}的前2n项和．‎ ‎34．（2016•上海）对于无穷数列{an}与{bn}，记A={x|x=an，n∈N*}，B={x|x=bn，n∈N*}，若同时满足条件：①{an}，{bn}均单调递增；②A∩B=∅且A∪B=N*，则称{an}与{bn}是无穷互补数列．‎ ‎（1）若an=2n﹣1，bn=4n﹣2，判断{an}与{bn}是否为无穷互补数列，并说明理由；‎ ‎（2）若an=2n且{an}与{bn}是无穷互补数列，求数量{bn}的前16项的和；‎ ‎（3）若{an}与{bn}是无穷互补数列，{an}为等差数列且a16=36，求{an}与{bn}的通项公式．‎ ‎35．（2016•新课标Ⅲ）已知数列{an}的前n项和Sn=1+λan，其中λ≠0．‎ ‎（1）证明{an}是等比数列，并求其通项公式；‎ ‎（2）若S5=，求λ．‎ ‎36．（2016•浙江）设数列{an}的前n项和为Sn，已知S2=4，an+1=2Sn+1，n∈N*．‎ ‎（Ⅰ）求通项公式an；‎ ‎（Ⅱ）求数列{|an﹣n﹣2|}的前n项和．‎ ‎37．（2016•新课标Ⅱ）Sn为等差数列{an}的前n项和，且a1=1，S7‎ ‎=28，记bn=[lgan]，其中[x]表示不超过x的最大整数，如[0.9]=0，[lg99]=1．‎ ‎（Ⅰ）求b1，b11，b101；‎ ‎（Ⅱ）求数列{bn}的前1000项和．‎ ‎38．（2016•四川）已知数列{an}的首项为1，Sn为数列{an}的前n项和，Sn+1=qSn+1，其中q＞0，n∈N+‎ ‎（Ⅰ）若a2，a3，a2+a3成等差数列，求数列{an}的通项公式；‎ ‎（Ⅱ）设双曲线x2﹣=1的离心率为en，且e2=2，求e12+e22+…+en2．‎ ‎39．（2016•新课标Ⅰ）已知{an}是公差为3的等差数列，数列{bn}满足b1=1，b2=，anbn+1+bn+1=nbn．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）求{bn}的前n项和．‎ ‎40．（2016•江苏）记U={1，2，…，100}，对数列{an}（n∈N*）和U的子集T，若T=∅，定义ST=0；若T={t1，t2，…，tk}，定义ST=++…+．例如：T={1，3，66}时，ST=a1+a3+a66．现设{an}（n∈N*）是公比为3的等比数列，且当T={2，4}时，ST=30．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）对任意正整数k（1≤k≤100），若T⊆{1，2，…，k}，求证：ST＜ak+1；‎ ‎（3）设C⊆U，D⊆U，SC≥SD，求证：SC+SC∩D≥2SD．‎ ‎　‎ ‎41、（2016•山东）已知数列{an}的前n项和Sn=3n2+8n，{bn}是等差数列，且an=bn+bn+1．‎ ‎（Ⅰ）求数列{bn}的通项公式；‎ ‎（Ⅱ）令cn=，求数列{cn}的前n项和Tn．‎ ‎42、（2016•新课标Ⅲ）已知各项都为正数的数列{an}满足a1=1，an2﹣（2an+1﹣1）an﹣2an+1=0．‎ ‎（1）求a2，a3；‎ ‎（2）求{an}的通项公式 高考数学真题汇编---数列 参考答案与试题解析 ‎　一．选择题（共9小题）‎ ‎1．‎ ‎【分析】利用等差数列通项公式及前n项和公式列出方程组，求出首项和公差，由此能求出{an}的公差．‎ ‎【解答】解：∵Sn为等差数列{an}的前n项和，a4+a5=24，S6=48，‎ ‎∴，‎ 解得a1=﹣2，d=4，‎ ‎∴{an}的公差为4．‎ 故选：C．‎ ‎　‎ ‎2．‎ ‎【分析】设塔顶的a1盏灯，由题意{an}是公比为2的等比数列，利用等比数列前n项和公式列出方程，能求出结果．‎ ‎【解答】解：设塔顶的a1盏灯，‎ 由题意{an}是公比为2的等比数列，‎ ‎∴S7==381，‎ 解得a1=3．‎ 故选：D．‎ ‎　‎ ‎3．‎ ‎【分析】利用等差数列通项公式、等比数列性质列出方程，求出公差，由此能求出{an}前6项的和．‎ ‎【解答】解：∵等差数列{an}的首项为1，公差不为0．a2，a3，a6成等比数列，‎ ‎∴，‎ ‎∴（a1+2d）2=（a1+d）（a1+5d），且a1=1，d≠0，‎ 解得d=﹣2，‎ ‎∴{an}前6项的和为==﹣24．‎ 故选：A．‎ ‎　‎ ‎4．‎ ‎【分析】方法一：由数列的性质，求得数列{bn}的通项公式及前n项和，可知当N为时（n∈N+），数列{an}的前N项和为数列{bn}的前n项和，即为2n+1﹣n﹣2，容易得到N＞100时，n≥14，分别判断，即可求得该款软件的激活码；‎ 方法二：由题意求得数列的每一项，及前n项和Sn=2n+1﹣2﹣n，及项数，由题意可知：2n+1为2的整数幂．只需将﹣2﹣n消去即可，分别即可求得N的值．‎ ‎【解答】解：设该数列为{an}，设bn=+…+=2n+1﹣1，（n∈N+），则=ai，‎ 由题意可设数列{an}的前N项和为SN，数列{bn}的前n项和为Tn，则Tn=21﹣1+22﹣1+…+2n+1﹣1=2n+1﹣n﹣2，‎ 可知当N为时（n∈N+），数列{an}的前N项和为数列{bn}的前n项和，即为2n+1﹣n﹣2，‎ 容易得到N＞100时，n≥14，‎ A项，由=435，440=435+5，可知S440=T29+b5=230﹣29﹣2+25﹣1=230，故A项符合题意．‎ B项，仿上可知=325，可知S330=T25+b5=226﹣25﹣2+25﹣1=226+4，显然不为2的整数幂，故B项不符合题意．‎ C项，仿上可知=210，可知S220=T20+b10=221﹣20﹣2+210﹣1=221+210‎ ‎﹣23，显然不为2的整数幂，故C项不符合题意．‎ D项，仿上可知=105，可知S110=T14+b5=215﹣14﹣2+25﹣1=215+15，显然不为2的整数幂，故D项不符合题意．‎ 故选A．‎ 方法二：由题意可知：，，，…，‎ 根据等比数列前n项和公式，求得每项和分别为：21﹣1，22﹣1，23﹣1，…，2n﹣1，‎ 每项含有的项数为：1，2，3，…，n，‎ 总共的项数为N=1+2+3+…+n=，‎ 所有项数的和为Sn：21﹣1+22﹣1+23﹣1+…+2n﹣1=（21+22+23+…+2n）﹣n=﹣n=2n+1﹣2﹣n，‎ 由题意可知：2n+1为2的整数幂．只需将﹣2﹣n消去即可，‎ 则①1+2+（﹣2﹣n）=0，解得：n=1，总共有+2=3，不满足N＞100，‎ ‎②1+2+4+（﹣2﹣n）=0，解得：n=5，总共有+3=18，不满足N＞100，‎ ‎③1+2+4+8+（﹣2﹣n）=0，解得：n=13，总共有+4=95，不满足N＞100，‎ ‎④1+2+4+8+16+（﹣2﹣n）=0，解得：n=29，总共有+5=440，满足N＞100，‎ ‎∴该款软件的激活码440．‎ 故选：A．‎ ‎　‎ ‎5．‎ ‎【分析】由已知推导出，由此利用排除法能求出结果．‎ ‎【解答】解：∵，S==，﹣1＜q＜1，‎ ‎2Sn＜S，‎ ‎∴，‎ 若a1＞0，则，故A与C不可能成立；‎ 若a1＜0，则qn，‎ 在B中，a1＜0，﹣0.7＜q＜﹣0.6故B成立；‎ 在D中，a1＜0，﹣0.8＜q＜﹣0.7，此时q2＞，D不成立．‎ 故选：B．‎ ‎　‎ ‎6．‎ ‎【分析】根据已知可得a5=3，进而求出公差，可得答案．‎ ‎【解答】解：∵等差数列{an}前9项的和为27，S9===9a5．‎ ‎∴9a5=27，a5=3，‎ 又∵a10=8，‎ ‎∴d=1，‎ ‎∴a100=a5+95d=98，‎ 故选：C．‎ ‎　‎ ‎7．‎ ‎【分析】设第n年开始超过200万元，可得130×（1+12%）n﹣2015＞200，两边取对数即可得出．‎ ‎【解答】解：设第n年开始超过200万元，‎ 则130×（1+12%）n﹣2015＞200，‎ 化为：（n﹣2015）lg1.12＞lg2﹣lg1.3，‎ n﹣2015＞=3.8．‎ 取n=2019．‎ 因此开始超过200万元的年份是2019年．‎ 故选：B．‎ ‎　‎ ‎8．‎ ‎【分析】设锐角的顶点为O，再设|OA1|=a，|OB1|=c，|AnAn+1|=|An+1An+2|=b，|BnBn+1|=|Bn+1Bn+2|=d，由于a，c不确定，判断C，D不正确，设△AnBnBn+1的底边BnBn+1上的高为hn，运用三角形相似知识，hn+hn+2=2hn+1，由Sn=d•hn，可得Sn+Sn+2=2Sn+1，进而得到数列{Sn}为等差数列．‎ ‎【解答】解：设锐角的顶点为O，|OA1|=a，|OB1|=c，‎ ‎|AnAn+1|=|An+1An+2|=b，|BnBn+1|=|Bn+1Bn+2|=d，‎ 由于a，c不确定，则{dn}不一定是等差数列，‎ ‎{dn2}不一定是等差数列，‎ 设△AnBnBn+1的底边BnBn+1上的高为hn，‎ 由三角形的相似可得==，‎ ‎==，‎ 两式相加可得，==2，‎ 即有hn+hn+2=2hn+1，‎ 由Sn=d•hn，可得Sn+Sn+2=2Sn+1，‎ 即为Sn+2﹣Sn+1=Sn+1﹣Sn，‎ 则数列{Sn}为等差数列．‎ 另解：可设△A1B1B2，△A2B2B3，…，AnBnBn+1为直角三角形，‎ 且A1B1，A2B2，…，AnBn为直角边，‎ 即有hn+hn+2=2hn+1，‎ 由Sn=d•hn，可得Sn+Sn+2=2Sn+1，‎ 即为Sn+2﹣Sn+1=Sn+1﹣Sn，‎ 则数列{Sn}为等差数列．‎ 故选：A．‎ ‎　‎ ‎9．‎ ‎【分析】由新定义可得，“规范01数列”有偶数项2m项，且所含0与1的个数相等，首项为0，末项为1，当m=4时，数列中有四个0和四个1，然后一一列举得答案．‎ ‎【解答】解：由题意可知，“规范01数列”有偶数项2m项，且所含0与1的个数相等，首项为0，末项为1，若m=4，说明数列有8项，满足条件的数列有：‎ ‎0，0，0，0，1，1，1，1； 0，0，0，1，0，1，1，1； 0，0，0，1，1，0，1，1； 0，0，0，1，1，1，0，1； 0，0，1，0，0，1，1，1；‎ ‎0，0，1，0，1，0，1，1； 0，0，1，0，1，1，0，1； 0，0，1，1，0，1，0，1； 0，0，1，1，0，0，1，1； 0，1，0，0，0，1，1，1；‎ ‎0，1，0，0，1，0，1，1； 0，1，0，0，1，1，0，1； 0，1，0，1，0，0，1，1； 0，1，0，1，0，1，0，1．共14个．‎ 故选：C．‎ ‎　‎ 二．填空题（共9小题）‎ ‎10．‎ ‎【分析】利用等差数列求出公差，等比数列求出公比，然后求解第二项，即可得到结果．‎ ‎【解答】解：等差数列{an}和等比数列{bn}满足a1=b1=﹣1，a4=b4=8，‎ 设等差数列的公差为d，等比数列的公比为q．‎ 可得：8=﹣1+3d，d=3，a2=2；‎ ‎8=﹣q3，解得q=﹣2，∴b2=2．‎ 可得=1．‎ 故答案为：1．‎ ‎　‎ ‎11．‎ ‎【分析】设等比数列{an}的公比为q≠1，S3=，S6=，可得=，=，联立解出即可得出．‎ ‎【解答】解：设等比数列{an}的公比为q≠1，‎ ‎∵S3=，S6=，∴=，=，‎ 解得a1=，q=2．‎ 则a8==32．‎ 故答案为：32．‎ ‎　‎ ‎12．‎ ‎【分析】利用已知条件求出等差数列的前n项和，然后化简所求的表达式，求解即可．‎ ‎【解答】解：等差数列{an}的前n项和为Sn，a3=3，S4=10，S4=2（a2+a3）=10，‎ 可得a2=2，数列的首项为1，公差为1，‎ Sn=，=，‎ 则 =2[1﹣++…+]=2（1﹣）=．‎ 故答案为：．‎ ‎　‎ ‎13．‎ ‎【分析】设等比数列{an}的公比为q，由a1+a2=﹣1，a1﹣a3=﹣3，可得：a1（1+q）=﹣1，a1（1﹣q2）=﹣3，解出即可得出．‎ ‎【解答】解：设等比数列{an}的公比为q，∵a1+a2=﹣1，a1﹣a3=﹣3，‎ ‎∴a1（1+q）=﹣1，a1（1﹣q2）=﹣3，‎ 解得a1=1，q=﹣2．‎ 则a4=（﹣2）3=﹣8．‎ 故答案为：﹣8．‎ ‎　‎ ‎14．‎ ‎【分析】利用等差数列的通项公式和前n项和公式列出方程组，求出首项和公差，由此能求出a9的值．‎ ‎【解答】解：∵{an}是等差数列，Sn是其前n项和，a1+a22=﹣3，S5=10，‎ ‎∴，‎ 解得a1=﹣4，d=3，‎ ‎∴a9=﹣4+8×3=20．‎ 故答案为：20．‎ ‎　‎ ‎15．‎ ‎【分析】由已知条件利用等差数列的性质求出公差，由此利用等差数列的前n项和公式能求出S6．‎ ‎【解答】解：∵{an}为等差数列，Sn为其前n项和．‎ a1=6，a3+a5=0，‎ ‎∴a1+2d+a1+4d=0，‎ ‎∴12+6d=0，‎ 解得d=﹣2，‎ ‎∴S6==36﹣30=6．‎ 故答案为：6．‎ ‎　‎ ‎16．‎ ‎【分析】对任意n∈N*，Sn∈{2，3}，列举出n=1，2，3，4的情况，归纳可得n＞4后都为0或1或﹣1，则k的最大个数为4．‎ ‎【解答】解：对任意n∈N*，Sn∈{2，3}，可得 当n=1时，a1=S1=2或3；‎ 若n=2，由S2∈{2，3}，可得数列的前两项为2，0；或2，1；或3，0；或3，﹣1；‎ 若n=3，由S3∈{2，3}，可得数列的前三项为2，0，0；或2，0，1；‎ 或2，1，0；或2，1，﹣1；或3，0，0；或3，0，﹣1；或3，1，0；或3，1，﹣1；‎ 若n=4，由S3∈{2，3}，可得数列的前四项为2，0，0，0；或2，0，0，1；‎ 或2，0，1，0；或2，0，1，﹣1；或2，1，0，0；或2，1，0，﹣1；‎ 或2，1，﹣1，0；或2，1，﹣1，1；或3，0，0，0；或3，0，0，﹣1；‎ 或3，0，﹣1，0；或3，0，﹣1，1；或3，﹣1，0，0；或3，﹣1，0，1；‎ 或3，﹣1，1，0；或3，﹣1，1，﹣1；‎ ‎…‎ 即有n＞4后一项都为0或1或﹣1，则k的最大个数为4，‎ 不同的四个数均为2，0，1，﹣1，或3，0，1，﹣1．‎ 故答案为：4．‎ ‎　‎ ‎17．‎ ‎【分析】求出数列的等比与首项，化简a1a2…an，然后求解最值．‎ ‎【解答】解：等比数列{an}满足a1+a3=10，a2+a4=5，‎ 可得q（a1+a3）=5，解得q=．‎ a1+q2a1=10，解得a1=8．‎ 则a1a2…an=a1n•q1+2+3+…+（n﹣1）=8n•==，‎ 当n=3或4时，表达式取得最大值：=26=64．‎ 故答案为：64．‎ ‎　‎ ‎18．‎ ‎【分析】运用n=1时，a1=S1，代入条件，结合S2=4，解方程可得首项；再由n＞1时，an+1=Sn+1﹣Sn，结合条件，计算即可得到所求和．‎ ‎【解答】解：由n=1时，a1=S1，可得a2=2S1+1=2a1+1，‎ 又S2=4，即a1+a2=4，‎ 即有3a1+1=4，解得a1=1；‎ 由an+1=Sn+1﹣Sn，可得 Sn+1=3Sn+1，‎ 由S2=4，可得S3=3×4+1=13，‎ S4=3×13+1=40，‎ S5=3×40+1=121．‎ 故答案为：1，121．‎ ‎　‎ 三．解答题（共22小题）‎ ‎19．‎ ‎【分析】（1）设等差数列{an}的公差为d，等比数列{bn}的公比为q，运用等差数列和等比数列的通项公式，列方程解方程可得d，q，即可得到所求通项公式；‎ ‎（2）运用等比数列的求和公式，解方程可得公比，再由等差数列的通项公式和求和，计算即可得到所求和．‎ ‎【解答】解：（1）设等差数列{an}的公差为d，等比数列{bn}的公比为q，‎ a1=﹣1，b1=1，a2+b2=2，a3+b3=5，‎ 可得﹣1+d+q=2，﹣1+2d+q2=5，‎ 解得d=1，q=2或d=3，q=0（舍去），‎ 则{bn}的通项公式为bn=2n﹣1，n∈N*；‎ ‎（2）b1=1，T3=21，‎ 可得1+q+q2=21，‎ 解得q=4或﹣5，‎ 当q=4时，b2=4，a2=2﹣4=﹣2，‎ d=﹣2﹣（﹣1）=﹣1，S3=﹣1﹣2﹣3=﹣6；‎ 当q=﹣5时，b2=﹣5，a2=2﹣（﹣5）=7，‎ d=7﹣（﹣1）=8，S3=﹣1+7+15=21．‎ ‎　‎ ‎20．‎ ‎【分析】（I）列方程组求出首项和公比即可得出通项公式；‎ ‎（II）从各点向x轴作垂线，求出梯形的面积的通项公式，利用错位相减法求和即可．‎ ‎【解答】解：（I）设数列{xn}的公比为q，则q＞0，‎ 由题意得，‎ 两式相比得：，解得q=2或q=﹣（舍），‎ ‎∴x1=1，‎ ‎∴xn=2n﹣1．‎ ‎（II）过P1，P2，P3，…，Pn向x轴作垂线，垂足为Q1，Q2，Q3，…，Qn，‎ 记梯形PnPn+1Qn+1Qn的面积为bn，‎ 则bn==（2n+1）×2n﹣2，‎ ‎∴Tn=3×2﹣1+5×20+7×21+…+（2n+1）×2n﹣2，①‎ ‎∴2Tn=3×20+5×21+7×22+…+（2n+1）×2n﹣1，②‎ ‎①﹣②得：﹣Tn=+（2+22+…+2n﹣1）﹣（2n+1）×2n﹣1‎ ‎=+﹣（2n+1）×2n﹣1=﹣+（1﹣2n）×2n﹣1．‎ ‎∴Tn=．‎ ‎　‎ ‎21．‎ ‎【分析】（1）通过首项和公比，联立a1+a2=6、a1a2=a3，可求出a1=q=2，进而利用等比数列的通项公式可得结论；‎ ‎（2）利用等差数列的性质可知S2n+1=（2n+1）bn+1，结合S2n+1=bnbn+1可知bn=2n+1，进而可知=，利用错位相减法计算即得结论．‎ ‎【解答】解：（1）记正项等比数列{an}的公比为q，‎ 因为a1+a2=6，a1a2=a3，‎ 所以（1+q）a1=6，q=q2a1，‎ 解得：a1=q=2，‎ 所以an=2n；‎ ‎（2）因为{bn} 为各项非零的等差数列，‎ 所以S2n+1=（2n+1）bn+1，‎ 又因为S2n+1=bnbn+1，‎ 所以bn=2n+1，=，‎ 所以Tn=3•+5•+…+（2n+1）•，‎ Tn=3•+5•+…+（2n﹣1）•+（2n+1）•，‎ 两式相减得：Tn=3•+2（++…+）﹣（2n+1）•，‎ 即Tn=3•+（+++…+）﹣（2n+1）•，‎ 即Tn=3+1++++…+）﹣（2n+1）•=3+﹣（2n+1）•‎ ‎=5﹣．‎ ‎　‎ ‎22．‎ ‎【分析】（Ⅰ）设等差数列{an}的公差为d，等比数列{bn}的公比为q．通过b2+b3=12，求出q，得到．然后求出公差d，推出an=3n﹣2．‎ ‎（Ⅱ）设数列{a2nbn}的前n项和为Tn，利用错位相减法，转化求解数列{a2nbn}的前n项和即可．‎ ‎【解答】（Ⅰ）解：设等差数列{an}的公差为d，等比数列{bn}的公比为q．由已知b2+b3=12，得，而b1=2，所以q2+q﹣6=0．又因为q＞0，解得q=2．所以，．‎ 由b3=a4﹣2a1，可得3d﹣a1=8．‎ 由S11=11b4，可得a1+5d=16，联立①②，解得a1=1，d=3，‎ 由此可得an=3n﹣2．‎ 所以，{an}的通项公式为an=3n﹣2，{bn}的通项公式为．‎ ‎（Ⅱ）解：设数列{a2nbn}的前n项和为Tn，由a2n=6n﹣2，有，，‎ 上述两式相减，得=．‎ 得．‎ 所以，数列{a2nbn}的前n项和为（3n﹣4）2n+2+16．‎ ‎　‎ ‎23．‎ ‎【分析】（Ⅰ）设出公差与公比，利用已知条件求出公差与公比，然后求解{an}和{bn}的通项公式；‎ ‎（Ⅱ）化简数列的通项公式，利用错位相减法求解数列的和即可．‎ ‎【解答】解：（I）设等差数列{an}的公差为d，等比数列{bn}的公比为q．‎ 由已知b2+b3=12，得b1（q+q2）=12，而b1=2，所以q+q2﹣6=0．‎ 又因为q＞0，解得q=2．所以，bn=2n．‎ 由b3=a4﹣2a1，可得3d﹣a1=8①．‎ 由S11=11b4，可得a1+5d=16②，‎ 联立①②，解得a1=1，d=3，由此可得an=3n﹣2．‎ 所以，数列{an}的通项公式为an=3n﹣2，数列{bn}的通项公式为bn=2n．‎ ‎（II）设数列{a2nb2n﹣1}的前n项和为Tn，‎ 由a2n=6n﹣2，b2n﹣1=4n，有a2nb2n﹣1=（3n﹣1）4n，‎ 故Tn=2×4+5×42+8×43+…+（3n﹣1）4n，‎ ‎4Tn=2×42+5×43+8×44+…+（3n﹣1）4n+1，‎ 上述两式相减，得﹣3Tn=2×4+3×42+3×43+…+3×4n﹣（3n﹣1）4n+1‎ ‎==﹣（3n﹣2）4n+1﹣8‎ 得Tn=．‎ 所以，数列{a2nb2n﹣1}的前n项和为．‎ ‎　‎ ‎24．‎ ‎【分析】（1）利用数列递推关系即可得出．‎ ‎（2）==﹣．利用裂项求和方法即可得出．‎ ‎【解答】解：（1）数列{an}满足a1+3a2+…+（2n﹣1）an=2n．‎ n≥2时，a1+3a2+…+（2n﹣3）an﹣1=2（n﹣1）．‎ ‎∴（2n﹣1）an=2．∴an=．‎ 当n=1时，a1=2，上式也成立．‎ ‎∴an=．‎ ‎（2）==﹣．‎ ‎∴数列{}的前n项和=++…+=1﹣=．‎ ‎　‎ ‎25．‎ ‎【分析】（1）由题意可知a3=S3﹣S2=﹣6﹣2=﹣8，a1==，a2==，由a1+a2=2，列方程即可求得q及a1，根据等比数列通项公式，即可求得{an}的通项公式；‎ ‎（2）由（1）可知．利用等比数列前n项和公式，即可求得Sn，分别求得Sn+1，Sn+2，显然Sn+1+Sn+2=2Sn，则Sn+1，Sn，Sn+2成等差数列．‎ ‎【解答】解：（1）设等比数列{an}首项为a1，公比为q，‎ 则a3=S3﹣S2=﹣6﹣2=﹣8，则a1==，a2==，‎ 由a1+a2=2，+=2，整理得：q2+4q+4=0，解得：q=﹣2，‎ 则a1=﹣2，an=（﹣2）（﹣2）n﹣1=（﹣2）n，‎ ‎∴{an}的通项公式an=（﹣2）n；‎ ‎（2）由（1）可知：Sn===﹣[2+（﹣2）n+1]，‎ 则Sn+1=﹣[2+（﹣2）n+2]，Sn+2=﹣[2+（﹣2）n+3]，‎ 由Sn+1+Sn+2=﹣[2+（﹣2）n+2]﹣[2+（﹣2）n+3]，‎ ‎=﹣[4+（﹣2）×（﹣2）n+1+（﹣2）2×（﹣2）n+1]，‎ ‎=﹣[4+2（﹣2）n+1]=2×[﹣（2+（﹣2）n+1）]，‎ ‎=2Sn，‎ 即Sn+1+Sn+2=2Sn，‎ ‎∴Sn+1，Sn，Sn+2成等差数列．‎ ‎　‎ ‎26．‎ ‎【分析】（1）由题意可知根据等差数列的性质，an﹣3+an﹣2+an﹣1+an+1+an+2+an+3=（an﹣3+an+3）+（an﹣2+an+2）+（an﹣1+an+1）═2×3an，根据“P（k）数列”的定义，可得数列{an}是“P（3）数列”；‎ ‎（2）由已知条件结合（1）中的结论，可得到{an}从第3项起为等差数列，再通过判断a2与a3的关系和a1与a2的关系，可知{an}为等差数列．‎ ‎【解答】解：（1）证明：设等差数列{an}首项为a1，公差为d，则an=a1+（n﹣1）d，‎ 则an﹣3+an﹣2+an﹣1+an+1+an+2+an+3，‎ ‎=（an﹣3+an+3）+（an﹣2+an+2）+（an﹣1+an+1），‎ ‎=2an+2an+2an，‎ ‎=2×3an，‎ ‎∴等差数列{an}是“P（3）数列”；‎ ‎（2）证明：当n≥4时，因为数列{an}是P（3）数列，则an﹣3+an﹣2+an﹣1+an+1+an+2+an+3=6an，①‎ 因为数列{an}是“P（2）数列”，所以an﹣2+an﹣1+an+1+an+2=4an，②‎ 则an﹣1+an+an+2+an+3=4an+1，③，‎ ‎②+③﹣①，得2an=4an﹣1+4an+1﹣6an，即2an=an﹣1+an+1，（n≥4），‎ 因此n≥4从第3项起为等差数列，设公差为d，注意到a2+a3+a5+a6=4a4，‎ 所以a2=4a4﹣a3﹣a5﹣a6=4（a3+d）﹣a3﹣（a3+2d）﹣（a3+3d）=a3﹣d，‎ 因为a1+a2+a4+a5=4a3，所以a1=4a3﹣a2﹣a4﹣a5=4（a2+d）﹣a2﹣（a2+2d）﹣（a2+3d）=a2﹣d，‎ 也即前3项满足等差数列的通项公式，‎ 所以{an}为等差数列．‎ ‎　‎ ‎27．‎ ‎【分析】（Ⅰ）利用已知条件求出等差数列的公差，然后求{an}的通项公式；‎ ‎（Ⅱ）利用已知条件求出公比，然后求解数列的和即可．‎ ‎【解答】解：（Ⅰ）等差数列{an}，a1=1，a2+a4=10，可得：1+d+1+3d=10，解得d=2，‎ 所以{an}的通项公式：an=1+（n﹣1）×2=2n﹣1．‎ ‎（Ⅱ）由（Ⅰ）可得a5=a1+4d=9，‎ 等比数列{bn}满足b1=1，b2b4=9．可得b3=3，或﹣3（舍去）（等比数列奇数项符号相同）．‎ ‎∴q2=3，‎ ‎{b2n﹣1}是等比数列，公比为3，首项为1．‎ b1+b3+b5+…+b2n﹣1==．‎ ‎　‎ ‎28．‎ ‎【分析】（1）分别求得a1=1，a2=2，a3=3，b1=1，b2=3，b3=5，代入即可求得c1，c2，c3；由（bk﹣nak）﹣（b1﹣na1）≤0，则b1﹣na1≥bk﹣nak，则cn=b1﹣na1=1﹣n，cn+1﹣cn=﹣1对∀n∈N*均成立；‎ ‎（2）由bi﹣ain=[b1+（i﹣1）d1]﹣[a1+（i﹣1）d2]×n=（b1﹣a1n）+（i﹣1）（d2﹣d1×n），分类讨论d1=0，d1＞0，d1＜0三种情况进行讨论根据等差数列的性质，即可求得使得cm，cm+1，cm+2，…是等差数列；设=An+B+‎ 对任意正整数M，存在正整数m，使得n≥m，＞M，分类讨论，采用放缩法即可求得因此对任意正数M，存在正整数m，使得当n≥m时，＞M．‎ ‎【解答】解：（1）a1=1，a2=2，a3=3，b1=1，b2=3，b3=5，‎ 当n=1时，c1=max{b1﹣a1}=max{0}=0，‎ 当n=2时，c2=max{b1﹣2a1，b2﹣2a2}=max{﹣1，﹣1}=﹣1，‎ 当n=3时，c3=max{b1﹣3a1，b2﹣3a2，b3﹣3a3}=max{﹣2，﹣3，﹣4}=﹣2，‎ 下面证明：对∀n∈N*，且n≥2，都有cn=b1﹣na1，‎ 当n∈N*，且2≤k≤n时，‎ 则（bk﹣nak）﹣（b1﹣na1），‎ ‎=[（2k﹣1）﹣nk]﹣1+n，‎ ‎=（2k﹣2）﹣n（k﹣1），‎ ‎=（k﹣1）（2﹣n），由k﹣1＞0，且2﹣n≤0，‎ 则（bk﹣nak）﹣（b1﹣na1）≤0，则b1﹣na1≥bk﹣nak，‎ 因此，对∀n∈N*，且n≥2，cn=b1﹣na1=1﹣n，‎ cn+1﹣cn=﹣1，‎ ‎∴c2﹣c1=﹣1，‎ ‎∴cn+1﹣cn=﹣1对∀n∈N*均成立，‎ ‎∴数列{cn}是等差数列；‎ ‎（2）证明：设数列{an}和{bn}的公差分别为d1，d2，下面考虑的cn取值，‎ 由b1﹣a1n，b2﹣a2n，…，bn﹣ann，‎ 考虑其中任意bi﹣ain，（i∈N*，且1≤i≤n），‎ 则bi﹣ain=[b1+（i﹣1）d1]﹣[a1+（i﹣1）d2]×n，‎ ‎=（b1﹣a1n）+（i﹣1）（d2﹣d1×n），‎ 下面分d1=0，d1＞0，d1＜0三种情况进行讨论，‎ ‎①若d1=0，则bi﹣ain═（b1﹣a1n）+（i﹣1）d2，‎ 当若d2≤0，则（bi﹣ain）﹣（b1﹣a1n）=（i﹣1）d2≤0，‎ 则对于给定的正整数n而言，cn=b1﹣a1n，此时cn+1﹣cn=﹣a1，‎ ‎∴数列{cn}是等差数列；‎ 当d2＞0，（bi﹣ain）﹣（bn﹣ann）=（i﹣n）d2＞0，‎ 则对于给定的正整数n而言，cn=bn﹣ann=bn﹣a1n，‎ 此时cn+1﹣cn=d2﹣a1，‎ ‎∴数列{cn}是等差数列；‎ 此时取m=1，则c1，c2，…，是等差数列，命题成立；‎ ‎②若d1＞0，则此时﹣d1n+d2为一个关于n的一次项系数为负数的一次函数，‎ 故必存在m∈N*，使得n≥m时，﹣d1n+d2＜0，‎ 则当n≥m时，（bi﹣ain）﹣（b1﹣a1n）=（i﹣1）（﹣d1n+d2）≤0，（i∈N*，1≤i≤n），‎ 因此当n≥m时，cn=b1﹣a1n，‎ 此时cn+1﹣cn=﹣a1，故数列{cn}从第m项开始为等差数列，命题成立；‎ ‎③若d1＜0，此时﹣d1n+d2为一个关于n的一次项系数为正数的一次函数，‎ 故必存在s∈N*，使得n≥s时，﹣d1n+d2＞0，‎ 则当n≥s时，（bi﹣ain）﹣（bn﹣ann）=（i﹣1）（﹣d1n+d2）≤0，（i∈N*，1≤i≤n），‎ 因此，当n≥s时，cn=bn﹣ann，‎ 此时==﹣an+，‎ ‎=﹣d2n+（d1﹣a1+d2）+，‎ 令﹣d1=A＞0，d1﹣a1+d2=B，b1﹣d2=C，‎ 下面证明：=An+B+对任意正整数M，存在正整数m，使得n≥m，＞M，‎ 若C≥0，取m=[+1]，[x]表示不大于x的最大整数，‎ 当n≥m时，≥An+B≥Am+B=A[+1]+B＞A•+B=M，‎ 此时命题成立；‎ 若C＜0，取m=[]+1，‎ 当n≥m时，‎ ‎≥An+B+≥Am+B+C＞A•+B+C≥M﹣C﹣B+B+C=M，‎ 此时命题成立，‎ 因此对任意正数M，存在正整数m，使得当n≥m时，＞M；‎ 综合以上三种情况，命题得证．‎ ‎　‎ ‎29．‎ ‎【分析】（Ⅰ）用数学归纳法即可证明，‎ ‎（Ⅱ）构造函数，利用导数判断函数的单调性，把数列问题转化为函数问题，即可证明，‎ ‎（Ⅲ）由≥2xn+1﹣xn得﹣≥2（﹣）＞0，继续放缩即可证明 ‎【解答】解：（Ⅰ）用数学归纳法证明：xn＞0，‎ 当n=1时，x1=1＞0，成立，‎ 假设当n=k时成立，则xk＞0，‎ 那么n=k+1时，若xk+1＜0，则0＜xk=xk+1+ln（1+xk+1）＜0，矛盾，‎ 故xn+1＞0，‎ 因此xn＞0，（n∈N*）‎ ‎∴xn=xn+1+ln（1+xn+1）＞xn+1，‎ 因此0＜xn+1＜xn（n∈N*），‎ ‎（Ⅱ）由xn=xn+1+ln（1+xn+1）得xnxn+1﹣4xn+1+2xn=xn+12﹣2xn+1+（xn+1+2）ln（1+xn+1），‎ 记函数f（x）=x2﹣2x+（x+2）ln（1+x），x≥0‎ ‎∴f′（x）=+ln（1+x）＞0，‎ ‎∴f（x）在（0，+∞）上单调递增，‎ ‎∴f（x）≥f（0）=0，‎ 因此xn+12﹣2xn+1+（xn+1+2）ln（1+xn+1）≥0，‎ 故2xn+1﹣xn≤；‎ ‎（Ⅲ）∵xn=xn+1+ln（1+xn+1）≤xn+1+xn+1=2xn+1，‎ ‎∴xn≥，‎ 由≥2xn+1﹣xn得﹣≥2（﹣）＞0，‎ ‎∴﹣≥2（﹣）≥…≥2n﹣1（﹣）=2n﹣2，‎ ‎∴xn≤，‎ 综上所述≤xn≤．‎ ‎　‎ ‎30．‎ ‎【分析】（1）设{an}是公差为d的等差数列，{bn}是公比为q的等比数列，运用通项公式可得q=3，d=2，进而得到所求通项公式；‎ ‎（2）求得cn=an+bn=2n﹣1+3n﹣1，再由数列的求和方法：分组求和，运用等差数列和等比数列的求和公式，计算即可得到所求和．‎ ‎【解答】解：（1）设{an}是公差为d的等差数列，‎ ‎{bn}是公比为q的等比数列，‎ 由b2=3，b3=9，可得q==3，‎ bn=b2qn﹣2=3•3n﹣2=3n﹣1；‎ 即有a1=b1=1，a14=b4=27，‎ 则d==2，‎ 则an=a1+（n﹣1）d=1+2（n﹣1）=2n﹣1；‎ ‎（2）cn=an+bn=2n﹣1+3n﹣1，‎ 则数列{cn}的前n项和为 ‎（1+3+…+（2n﹣1））+（1+3+9+…+3n﹣1）=n•2n+‎ ‎=n2+．‎ ‎　‎ ‎31．‎ ‎【分析】（Ⅰ）结合“G时刻”的定义进行分析；‎ ‎（Ⅱ）可以采用假设法和递推法进行分析；‎ ‎（Ⅲ）可以采用假设法和列举法进行分析．‎ ‎【解答】解：（Ⅰ）根据题干可得，a1=﹣2，a2=2，a3=﹣1，a4=1，a5=3，a1＜a2满足条件，2满足条件，a2＞a3不满足条件，3不满足条件，‎ a2＞a4不满足条件，4不满足条件，a1，a2，a3，a4，均小于a5，因此5满足条件，因此G（A）={2，5}．‎ ‎（Ⅱ）因为存在an＞a1，设数列A中第一个大于a1的项为ak，则ak＞a1≥ai，其中2≤i≤k﹣1，所以k∈G（A），G（A）≠∅；‎ ‎（Ⅲ）设A数列的所有“G时刻”为i1＜i2＜…＜ik，‎ 对于第一个“G时刻”i1，有＞a1≥ai（i=2，3，…，i1﹣1），则 ‎﹣a1≤﹣≤1．‎ 对于第二个“G时刻”i1，有＞≥ai（i=2，3，…，i1﹣1），则 ‎﹣≤﹣≤1．‎ 类似的﹣≤1，…，﹣≤1．‎ 于是，k≥（﹣）+（﹣）+…+（﹣）+（﹣a1）=﹣a1．‎ 对于aN，若N∈G（A），则=aN．‎ 若N∉G（A），则aN≤，否则由（2）知，，…，aN，中存在“G时刻”与只有k个“G时刻”矛盾．‎ 从而k≥﹣a1≥aN﹣a1．‎ ‎　‎ ‎32．‎ ‎【分析】（Ⅰ）设等差数列{an}的公差为d，根据已知构造关于首项和公差方程组，解得答案；‎ ‎（Ⅱ）根据bn=[an]，列出数列{bn}的前10项，相加可得答案．‎ ‎【解答】解：（Ⅰ）设等差数列{an}的公差为d，‎ ‎∵a3+a4=4，a5+a7=6．‎ ‎∴，‎ 解得：，‎ ‎∴an=；‎ ‎（Ⅱ）∵bn=[an]，‎ ‎∴b1=b2=b3=1，‎ b4=b5=2，‎ b6=b7=b8=3，‎ b9=b10=4．‎ 故数列{bn}的前10项和S10=3×1+2×2+3×3+2×4=24．‎ ‎　‎ ‎33．‎ ‎【分析】（1）根据等比数列的通项公式列方程解出公比q，利用求和公式解出a1，得出通项公式；‎ ‎（2）利用对数的运算性质求出bn，使用分项求和法和平方差公式计算．‎ ‎【解答】解：（1）设{an}的公比为q，则﹣=，即1﹣=，‎ 解得q=2或q=﹣1．‎ 若q=﹣1，则S6=0，与S6=63矛盾，不符合题意．∴q=2，‎ ‎∴S6==63，∴a1=1．‎ ‎∴an=2n﹣1．‎ ‎（2）∵bn是log2an和log2an+1的等差中项，‎ ‎∴bn=（log2an+log2an+1）=（log22n﹣1+log22n）=n﹣．‎ ‎∴bn+1﹣bn=1．‎ ‎∴{bn}是以为首项，以1为公差的等差数列．‎ 设{（﹣1）nbn2}的前2n项和为Tn，则 Tn=（﹣b12+b22）+（﹣b32+b42）+…+（﹣b2n﹣12+b2n2）‎ ‎=b1+b2+b3+b4…+b2n﹣1+b2n ‎==‎ ‎=2n2．‎ ‎　‎ ‎34．‎ ‎【分析】（1）{an}与{bn}不是无穷互补数列．由4∉A，4∉B，4∉A∪B=N*，即可判断；‎ ‎（2）由an=2n，可得a4=16，a5=32，再由新定义可得b16=16+4=20，运用等差数列的求和公式，计算即可得到所求和；‎ ‎（3）运用等差数列的通项公式，结合首项大于等于1，可得d=1或2，讨论d=1，2求得通项公式，结合新定义，即可得到所求数列的通项公式．‎ ‎【解答】解：（1）{an}与{bn}不是无穷互补数列．‎ 理由：由an=2n﹣1，bn=4n﹣2，可得4∉A，4∉B，‎ 即有4∉A∪B=N*，即有{an}与{bn}不是无穷互补数列；‎ ‎（2）由an=2n，可得a4=16，a5=32，‎ 由{an}与{bn}是无穷互补数列，可得b16=16+4=20，‎ 即有数列{bn}的前16项的和为 ‎（1+2+3+…+20）﹣（2+4+8+16）=×20﹣30=180；‎ ‎（3）设{an}为公差为d（d为正整数）的等差数列且a16=36，则a1+15d=36，‎ 由a1=36﹣15d≥1，可得d=1或2，‎ 若d=1，则a1=21，an=n+20，bn=n（1≤n≤20），‎ 与{an}与{bn}是无穷互补数列矛盾，舍去；‎ 若d=2，则a1=6，an=2n+4，bn=．‎ 综上可得，an=2n+4，bn=．‎ ‎　‎ ‎35．‎ ‎【分析】（1）根据数列通项公式与前n项和公式之间的关系进行递推，结合等比数列的定义进行证明求解即可．‎ ‎（2）根据条件建立方程关系进行求解就可．‎ ‎【解答】解：（1）∵Sn=1+λan，λ≠0．‎ ‎∴an≠0．‎ 当n≥2时，an=Sn﹣Sn﹣1=1+λan﹣1﹣λan﹣1=λan﹣λan﹣1，‎ 即（λ﹣1）an=λan﹣1，‎ ‎∵λ≠0，an≠0．∴λ﹣1≠0．即λ≠1，‎ 即=，（n≥2），‎ ‎∴{an}是等比数列，公比q=，‎ 当n=1时，S1=1+λa1=a1，‎ 即a1=，‎ ‎∴an=•（）n﹣1．‎ ‎（2）若S5=，‎ 则若S5=1+λ[•（）4]=，‎ 即（）5=﹣1=﹣，‎ 则=﹣，得λ=﹣1．‎ ‎　‎ ‎36．‎ ‎【分析】（Ⅰ）根据条件建立方程组关系，求出首项，利用数列的递推关系证明数列{an}是公比q=3的等比数列，即可求通项公式an；‎ ‎（Ⅱ）讨论n的取值，利用分组法将数列转化为等比数列和等差数列即可求数列{|an﹣n﹣2|}的前n项和．‎ ‎【解答】解：（Ⅰ）∵S2=4，an+1=2Sn+1，n∈N*．‎ ‎∴a1+a2=4，a2=2S1+1=2a1+1，‎ 解得a1=1，a2=3，‎ 当n≥2时，an+1=2Sn+1，an=2Sn﹣1+1，‎ 两式相减得an+1﹣an=2（Sn﹣Sn﹣1）=2an，‎ 即an+1=3an，当n=1时，a1=1，a2=3，‎ 满足an+1=3an，‎ ‎∴=3，则数列{an}是公比q=3的等比数列，‎ 则通项公式an=3n﹣1．‎ ‎（Ⅱ）an﹣n﹣2=3n﹣1﹣n﹣2，‎ 设bn=|an﹣n﹣2|=|3n﹣1﹣n﹣2|，‎ 则b1=|30﹣1﹣2|=2，b2=|3﹣2﹣2|=1，‎ 当n≥3时，3n﹣1﹣n﹣2＞0，‎ 则bn=|an﹣n﹣2|=3n﹣1﹣n﹣2，‎ 此时数列{|an﹣n﹣2|}的前n项和Tn=3+﹣=，‎ 则Tn==．‎ ‎　‎ ‎37．‎ ‎【分析】（Ⅰ）利用已知条件求出等差数列的公差，求出通项公式，然后求解b1，b11，b101；‎ ‎（Ⅱ）找出数列的规律，然后求数列{bn}的前1000项和．‎ ‎【解答】解：（Ⅰ）Sn为等差数列{an}的前n项和，且a1=1，S7=28，7a4=28．‎ 可得a4=4，则公差d=1．‎ an=n，‎ bn=[lgn]，则b1=[lg1]=0，‎ b11=[lg11]=1，‎ b101=[lg101]=2．‎ ‎（Ⅱ）由（Ⅰ）可知：b1=b2=b3=…=b9=0，b10=b11=b12=…=b99=1．‎ b100=b101=b102=b103=…=b999=2，b10，00=3．‎ 数列{bn}的前1000项和为：9×0+90×1+900×2+3=1893．‎ ‎　‎ ‎38．‎ ‎【分析】（Ⅰ）根据题意，由数列的递推公式可得a2与a3的值，又由a2，a3，a2+a3成等差数列，可得2a3=a2+（a2+a3），代入a2与a3的值可得q2=2q，解可得q的值，进而可得Sn+1=2Sn+1，进而可得Sn=2Sn﹣1+1，将两式相减可得an=2an﹣1，即可得数列{an}是以1为首项，公比为2的等比数列，由等比数列的通项公式计算可得答案；‎ ‎（Ⅱ）根据题意Sn+1=qSn+1，同理有Sn=qSn﹣1+1，将两式相减可得an=qan﹣1，分析可得an=qn﹣1；又由双曲线x2﹣=1的离心率为en，且e2=2，分析可得e2==2，‎ 解可得a2的值，由an=qn﹣1可得q的值，进而可得数列{an}的通项公式，再次由双曲线的几何性质可得en2=1+an2=1+3n﹣1，运用分组求和法计算可得答案．‎ ‎【解答】解：（Ⅰ）根据题意，数列{an}的首项为1，即a1=1，‎ 又由Sn+1=qSn+1，则S2=qa1+1，则a2=q，‎ 又有S3=qS2+1，则有a3=q2，‎ 若a2，a3，a2+a3成等差数列，即2a3=a2+（a2+a3），‎ 则可得q2=2q，（q＞0），‎ 解可得q=2，‎ 则有Sn+1=2Sn+1，①‎ 进而有Sn=2Sn﹣1+1，②‎ ‎①﹣②可得an=2an﹣1，‎ 则数列{an}是以1为首项，公比为2的等比数列，‎ 则an=1×2n﹣1=2n﹣1；‎ ‎（Ⅱ）根据题意，有Sn+1=qSn+1，③‎ 同理可得Sn=qSn﹣1+1，④‎ ‎③﹣④可得：an=qan﹣1，‎ 又由q＞0，‎ 则数列{an}是以1为首项，公比为q的等比数列，则an=1×qn﹣1=qn﹣1；‎ 若e2=2，则e2==2，‎ 解可得a2=，‎ 则a2=q=，即q=，‎ an=1×qn﹣1=qn﹣1=（）n﹣1，‎ 则en2=1+an2=1+3n﹣1，‎ 故e12+e22+…+en2=n+（1+3+32+…+3n﹣1）=n+．‎ ‎　‎ ‎39．‎ ‎【分析】（Ⅰ）令n=1，可得a1=2，结合{an}是公差为3的等差数列，可得{an}的通项公式；‎ ‎（Ⅱ）由（1）可得：数列{bn}是以1为首项，以为公比的等比数列，进而可得：{bn}的前n项和．‎ ‎【解答】解：（Ⅰ）∵anbn+1+bn+1=nbn．‎ 当n=1时，a1b2+b2=b1．‎ ‎∵b1=1，b2=，‎ ‎∴a1=2，‎ 又∵{an}是公差为3的等差数列，‎ ‎∴an=3n﹣1，‎ ‎（Ⅱ）由（I）知：（3n﹣1）bn+1+bn+1=nbn．‎ 即3bn+1=bn．‎ 即数列{bn}是以1为首项，以为公比的等比数列，‎ ‎∴{bn}的前n项和Sn==（1﹣3﹣n）=﹣．‎ ‎　‎ ‎40．‎ ‎【分析】（1）根据题意，由ST的定义，分析可得ST=a2+a4=a2+9a2=30，计算可得a2=3，进而可得a1的值，由等比数列通项公式即可得答案；‎ ‎（2）根据题意，由ST的定义，分析可得ST≤a1+a2+…ak=1+3+32+…+3k﹣1，由等比数列的前n项和公式计算可得证明；‎ ‎（3）设A=∁C（C∩D），B=∁D（C∩D），则A∩B=∅‎ ‎，进而分析可以将原命题转化为证明SC≥2SB，分2种情况进行讨论：①、若B=∅，②、若B≠∅，可以证明得到SA≥2SB，即可得证明．‎ ‎【解答】解：（1）等比数列{an}中，a4=3a3=9a2，‎ 当T={2，4}时，ST=a2+a4=a2+9a2=30，‎ 因此a2=3，从而a1==1，‎ 故an=3n﹣1，‎ ‎（2）ST≤a1+a2+…ak=1+3+32+…+3k﹣1=＜3k=ak+1，‎ ‎（3）设A=∁C（C∩D），B=∁D（C∩D），则A∩B=∅，‎ 分析可得SC=SA+SC∩D，SD=SB+SC∩D，则SC+SC∩D﹣2SD=SA﹣2SB，‎ 因此原命题的等价于证明SC≥2SB，‎ 由条件SC≥SD，可得SA≥SB，‎ ‎①、若B=∅，则SB=0，故SA≥2SB，‎ ‎②、若B≠∅，由SA≥SB可得A≠∅，设A中最大元素为l，B中最大元素为m，‎ 若m≥l+1，则其与SA＜ai+1≤am≤SB相矛盾，‎ 因为A∩B=∅，所以l≠m，则l≥m+1，‎ SB≤a1+a2+…am=1+3+32+…+3m﹣1=≤=，即SA≥2SB，‎ 综上所述，SA≥2SB，‎ 故SC+SC∩D≥2SD．‎ ‎　‎ ‎41、【分析】（Ⅰ）求出数列{an}的通项公式，再求数列{bn}的通项公式；‎ ‎（Ⅱ）求出数列{cn}的通项，利用错位相减法求数列{cn}的前n项和Tn．‎ ‎【解答】解：（Ⅰ）Sn=3n2+8n，‎ ‎∴n≥2时，an=Sn﹣Sn﹣1=6n+5，‎ n=1时，a1=S1=11，∴an=6n+5；‎ ‎∵an=bn+bn+1，‎ ‎∴an﹣1=bn﹣1+bn，‎ ‎∴an﹣an﹣1=bn+1﹣bn﹣1．‎ ‎∴2d=6，‎ ‎∴d=3，‎ ‎∵a1=b1+b2，‎ ‎∴11=2b1+3，‎ ‎∴b1=4，‎ ‎∴bn=4+3（n﹣1）=3n+1；‎ ‎（Ⅱ）cn========6（n+1）•2n，‎ ‎∴Tn=6[2•2+3•22+…+（n+1）•2n]①，‎ ‎∴2Tn=6[2•22+3•23+…+n•2n+（n+1）•2n+1]②，‎ ‎①﹣②可得 ‎﹣Tn=6[2•2+22+23+…+2n﹣（n+1）•2n+1]‎ ‎=12+6×﹣6（n+1）•2n+1‎ ‎=（﹣6n）•2n+1=﹣3n•2n+2，‎ ‎∴Tn=3n•2n+2．‎ ‎42、【分析】（1）根据题意，由数列的递推公式，令n=1可得a12﹣（2a2﹣1）a1﹣2a2=0，将a1=1代入可得a2的值，进而令n=2可得a22﹣（2a3﹣1）a2﹣2a3=0，将a2=代入计算可得a3的值，即可得答案；‎ ‎（2）根据题意，将an2﹣（2an+1﹣1）an﹣2an+1=0变形可得（an﹣2an+1）（an+an+1）=0，进而分析可得an=2an+1或an=﹣an+1，结合数列各项为正可得an=2an+1，结合等比数列的性质可得{an}是首项为a1=1，公比为的等比数列，由等比数列的通项公式计算可得答案．‎ ‎【解答】解：（1）根据题意，an2﹣（2an+1﹣1）an﹣2an+1=0，‎ 当n=1时，有a12﹣（2a2﹣1）a1﹣2a2=0，‎ 而a1=1，则有1﹣（2a2﹣1）﹣2a2=0，解可得a2=，‎ 当n=2时，有a22﹣（2a3﹣1）a2﹣2a3=0，‎ 又由a2=，解可得a3=，‎ 故a2=，a3=；‎ ‎（2）根据题意，an2﹣（2an+1﹣1）an﹣2an+1=0，‎ 变形可得（an﹣2an+1）（an+1）=0，‎ 即有an=2an+1或an=﹣1，‎ 又由数列{an}各项都为正数，‎ 则有an=2an+1，‎ 故数列{an}是首项为a1=1，公比为的等比数列，‎ 则an=1×（）n﹣1=（）n﹣1，‎ 故an=（）n﹣1．‎