【物理】2019届一轮复习人教版 　交变电流的产生和描述 学案 16页

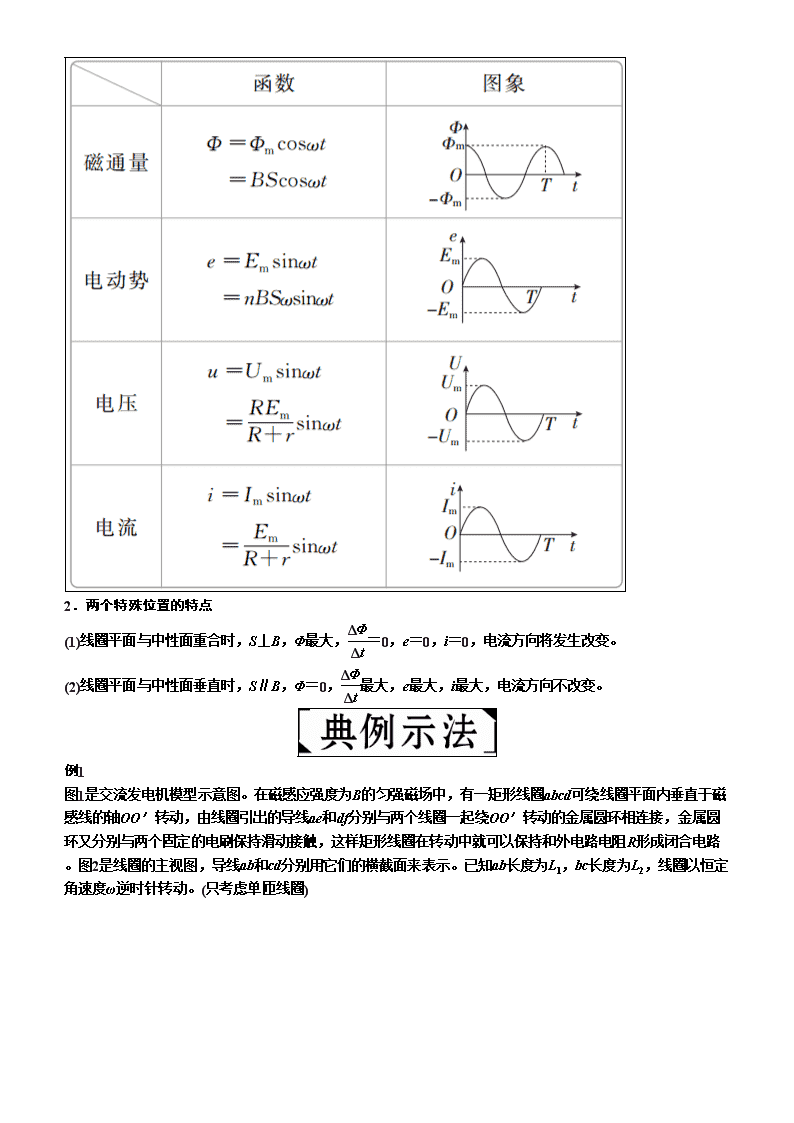
第1讲　交变电流的产生和描述 板块一　主干梳理·夯实基础　‎ ‎【知识点1】　交变电流、交变电流的图象　Ⅰ ‎1．交变电流 ‎(1)定义：大小和方向都随时间做周期性变化的电流叫做交变电流。‎ ‎(2)图象：图(a)、(b)、(c)、(d)所示电流都属于交变电流，其中按正弦规律变化的交变电流叫正弦式交变电流，如图(a)所示。‎ ‎2．正弦式交变电流的产生和变化规律 ‎(1)产生：在匀强磁场中，线圈绕垂直于磁场方向的轴匀速转动产生的电流是正弦式交变电流。‎ ‎(2)中性面 ‎①中性面：线圈平面与磁感线垂直的位置称为中性面。‎ ‎②中性面的特点以及与峰值面(中性面的垂面)的比较 ‎(3)正弦式交流电的图象：用以描述交变电流随时间变化的规律，如果从线圈位于中性面位置时开始计时，其图象为正弦曲线。如图甲、乙所示。‎ ‎(4)变化规律 正弦式交变电流的函数表达式(线圈在中性面位置时开始计时)‎ ‎①电动势e随时间变化的规律：e＝Emsinωt，其中ω表示线圈转动的角速度，Em＝nBSω。‎ ‎②负载两端的电压u随时间变化的规律：u＝Umsinωt。‎ ‎③电流i随时间变化的规律：i＝Imsinωt。‎ ‎【知识点2】　描述交变电流的物理量　Ⅰ ‎1．周期和频率 ‎(1)周期(T)：交变电流完成一次周期性变化(线圈转一周)所需的时间，单位是秒(s)，公式T＝。‎ ‎(2)频率(f)：交变电流在1 s内完成周期性变化的次数。单位是赫兹(Hz)。‎ ‎(3)周期和频率的关系：T＝或f＝。‎ ‎2．交变电流的瞬时值、峰值、有效值和平均值 ‎(1)瞬时值：交变电流的电动势、电流或电压在某一时刻的值，是时间的函数。‎ ‎(2)峰值：交变电流的电动势、电流或电压所能达到的最大值。‎ ‎(3)有效值 ‎①定义：让交流和直流通过相同阻值的电阻，如果它们在相同的时间内产生的热量相等，就把这一直流的数值叫做这一交流的有效值。‎ ‎②有效值和峰值的关系：E＝，U＝，I＝。(适用于正弦式交流电)‎ ‎(4)平均值：交变电流图象中波形与横轴所围面积跟时间的比值。‎ 板块二　考点细研·悟法培优 考点1正弦式电流的变化规律及应用[拓展延伸]‎ ‎1．正弦式交变电流的变化规律(线圈在中性面位置时开始计时)‎ ‎2．两个特殊位置的特点 ‎(1)线圈平面与中性面重合时，S⊥B，Φ最大，＝0，e＝0，i＝0，电流方向将发生改变。‎ ‎(2)线圈平面与中性面垂直时，S∥B，Φ＝0，最大，e最大，i最大，电流方向不改变。‎ 例1　图1是交流发电机模型示意图。在磁感应强度为B的匀强磁场中，有一矩形线圈abcd可绕线圈平面内垂直于磁感线的轴OO′转动，由线圈引出的导线ae和df分别与两个线圈一起绕OO′转动的金属圆环相连接，金属圆环又分别与两个固定的电刷保持滑动接触，这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路。图2是线圈的主视图，导线ab和cd分别用它们的横截面来表示。已知ab长度为L1，bc长度为L2，线圈以恒定角速度ω逆时针转动。(只考虑单匝线圈)‎ ‎(1)线圈平面处于中性面位置时开始计时，试推导t时刻整个线圈中的感应电动势e1的表达式；‎ ‎(2)线圈平面处于与中性面成φ0夹角位置时开始计时，如图3所示，试写出t时刻整个线圈中的感应电动势e2的表达式；‎ ‎(3)若线圈电阻为r，求线圈每转动一周电阻R上产生的焦耳热。(其他电阻均不计)‎ ‎(1)导线切割磁感线产生的感应电动势的表达式是_____________________________________________________________________________________________________________________________________________。‎ 提示：E＝Blvsinθ(θ为B与v方向间的夹角)‎ ‎(2)焦耳定律是________________________________________________________________________。‎ 提示：Q＝I2RT 尝试解答　(1)e1＝BL1L2ωsinωt ‎(2)e2＝BL1L2ωsin(ωt＋φ0)‎ ‎(3)πRω2。‎ ‎(1)矩形线圈abcd转动过程中，只有ab和cd导线切割磁感线，设ab和cd导线转动的线速度为v，则 v＝ω· 在t时刻，导线ab和cd因切割磁感线而产生的感应电动势均为 E1＝BL1vy 由图可知vy＝vsinωt 则整个线圈的感应电动势为 e1＝2E1＝BL1L2ωsinωt。‎ ‎(2)当线圈由图3位置开始转动时，在t时刻整个线圈的感应电动势为 e2＝BL1L2ωsin(ωt＋φ0)。‎ ‎(3)由闭合电路欧姆定律可知 I＝ E＝＝ 则线圈转动一周在R上产生的焦耳热为 QR＝I2RT 其中T＝ 于是QR＝πRω2。‎ 总结升华 解决交变电流图象问题的四点注意 ‎(1)只有当线圈从中性面位置开始计时，电流的瞬时值表达式才是正弦形式，其变化规律与线圈的形状及转动轴处于线圈平面内的位置无关。‎ ‎(2)注意峰值公式Em＝nBSω中的S为线框处于磁场中的有效面积。‎ ‎(3)在解决有关交变电流的图象问题时，应先把交变电流的图象与线圈的转动位置对应起来，再根据特殊位置求特殊解。‎ ‎(4)根据法拉第电磁感应定律E＝n，若Φ按余弦规律变化，则E必按正弦规律变化；Φ按正弦规律变化，E必按余弦规律变化，即Φ＝Φmsinωt，E＝nωΦmcosωt，故Φ增大时，E必减小；Φ最大时，E最小，Φ与E除系数不同外，二者具有“互余”关系。‎ 　[2017·湖北黄冈模拟]在匀强磁场中，一矩形金属线框绕与磁感线垂直的转轴匀速转动，如图甲所示，产生的交变电动势的图象如图乙所示，则(　　)‎ A．t＝0.005 s时线框的磁通量变化率为零 B．t＝0.01 s时线框平面与中性面重合 C．线框产生的交变电动势有效值为311 V D．线框产生的交变电动势频率为100 Hz 答案　B 解析　由题图乙可知，t＝0.005 s时，感应电动势最大，线框的磁通量变化率最大，A错误；t＝0.01 s时感应电动势为零，故线框平面处于中性面位置，B正确；交变电动势的最大值为311 V，故有效值E＝＝220‎ ‎ V，C错误；交变电动势的周期为T＝0.02 s，故频率f＝＝50 Hz，D错误。‎ 考点2交变电流的“四值”的比较[对比分析]‎ ‎1．交变电流的瞬时值、峰值、有效值和平均值的比较 ‎2．对交变电流有效值的理解 ‎(1)交变电流的有效值是根据电流的热效应(电流通过电阻生热)进行定义的，所以进行有效值计算时，要紧扣电流通过电阻生热(或热功率)进行计算。‎ ‎(2)注意“三同”：即“相同电阻”，“相同时间”内产生“相同热量”。‎ ‎(3)计算时“相同时间”一般取一个周期。‎ ‎3．书写交变电流瞬时值表达式的基本思路 ‎(1)求出角速度ω，ω＝＝2πf。‎ ‎(2)确定正弦式交变电流的峰值，根据已知图象读出或由公式Em＝nBSω求出相应峰值。‎ ‎(3)明确线圈的初始位置，找出对应的函数关系式。‎ 如：①线圈从中性面位置开始转动，则it图象为正弦函数图象，函数式为i＝Imsinωt。‎ ‎②线圈从垂直中性面位置开始转动，则it图象为余弦函数图象，函数式为i＝Imcosωt。‎ ‎4．记忆感应电动势表达式的“小技巧”‎ 根据特殊值及函数的增减性可帮助记忆：中性面处感应电动势为零。与B平行时，电动势最大。从中性面转到与中性面垂直的位置的过程中，感应电动势增大，故函数为增函数，表达式为e＝emsinωt，同理，从与B平行的位置开始转动时，函数为减函数，e＝emcosωt。‎ 例2　如图所示，一半径为r的半圆形单匝线圈垂直放在具有理想边界的匀强磁场中，磁场的磁感应强度为B。以直径ab为轴匀速转动，转速为n，ab与磁场边界重合，M和N是两个滑环，负载电阻为R。线圈、电流表和连接导线的电阻不计，下列说法中正确的是(　　)‎ A．转动过程中电流表的示数为 B．从图示位置起转过圈的时间内电阻R上产生的焦耳热是 C．从图示位置起转过圈的时间内通过负载电阻R的电荷量为 D．以上说法均不正确 ‎(1)电流表的读数是什么值？‎ 提示：有效值。‎ ‎(2)计算通过负载电阻R的电荷量用什么值？‎ 提示：平均值。‎ ‎(3)求焦耳热用什么值？‎ 提示：有效值。‎ 尝试解答　选A。‎ 转速为n，则ω＝2πn，S＝πr2，最大感应电动势Em＝BSω＝π2Bnr2，因只有一半区域内有磁场，由有效值的计算公式可得T＝2××得有效值E＝＝，则电路中电流I＝＝，故A正确；转圈时磁通量变化量为ΔΦ＝B，所用的时间t＝＝，则平均电动势＝＝2nπBr2，通过负载电阻R的电荷量q＝t＝t＝，C错误。求焦耳热要用有效值，Q＝I2Rt＝2·R·＝，B、D错误。‎ 总结升华 解决交变电流“四值”问题的关键 ‎(1)涉及到交流电表的读数，功、功率都用有效值。‎ ‎(2)涉及计算通过截面电荷量用平均值。‎ ‎(3)涉及电容器的击穿电压考虑峰值。‎ ‎(4)涉及到电流、电压随时间变化规律时，即与不同时刻有关，考虑瞬时值。‎ 　[2017·北京海淀期末]如图所示，位于竖直平面内的矩形金属线圈，边长l1＝0.40 m、l2＝0.25 m，其匝数n＝100匝，总电阻r＝1.0 Ω，线圈的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起，并通过电刷和R＝3.0 Ω的定值电阻相连接。线圈所在空间存在水平向右的匀强磁场，磁感应强度B＝1.0 T，在外力驱动下线圈绕竖直固定中心轴O1O2匀速转动，角速度ω＝2.0 rad/s。‎ ‎(1)求电阻R两端电压的最大值；‎ ‎(2)从线圈通过中性面(即线圈平面与磁场方向垂直的位置)开始计时，求经过周期通过电阻R的电荷量；‎ ‎(3)求在线圈转动一周的过程中，整个电路产生的焦耳热。‎ 答案　(1)15 V　(2)2.5 C　(3)约157 J 解析　(1)线圈中感应电动势的最大值Em＝nBSω，其中S＝l1l2‎ 所以Em＝nBl1l2ω＝20 V 线圈中感应电流的最大值Im＝＝5.0 A 电阻R两端电压的最大值Um＝ImR＝15 V。‎ ‎(2)从线圈通过中性面时开始，经过周期的时间 t＝＝ 此过程中线圈中的平均感应电动势＝n＝n 通过电阻R的平均电流＝＝，‎ 通过电阻R的电荷量q＝t＝＝2.5 C。‎ ‎(3)线圈中感应电流的有效值I＝＝ A 线圈转动一周的过程中，电流通过整个回路产生的焦耳热：Q热＝I2(R＋r)T＝50π J≈157 J。‎ 考点3交流电有效值的计算[拓展延伸]‎ ‎1．交变电流有效值的求解 ‎2．几种典型的交变电流及其有效值 例3　如图所示是某种交变电流的电流随时间变化的图线，i>0部分的图线是一个正弦曲线的正半周，i<0部分的图线是另一个正弦曲线的负半周，其最大值如图中所示，则这种交变电流的有效值为(　　)‎ A．I0 B.I0 C.I0 D.I0‎ ‎(1)0～T周期内，电流的有效值？‎ 提示：连续的正弦式交流电的有效值等于最大值除以。‎ ‎(2)0～3T周期内，电流的有效值怎么计算？‎ 提示：非连续的正弦式交流电的有效值按热效应来计算。‎ 尝试解答　选C。‎ 取一个周期时间，由电流的热效应求解；‎ 设电流的有效值为I，‎ 则I2R·3T＝2R·T＋2R·2T，解得I＝I0，故选项C正确。‎ 总结升华 ‎1．高中阶段可以定量求解有效值的只有正弦式交变电流(或其一部分)，方波式电流及其组合。‎ ‎2．遇到完整的正弦(余弦)函数图象，正弦式正向脉动交流电可根据I有＝，E有＝，U有＝求解。‎ ‎3．正弦式半波、矩形脉动等交流电只能利用电流热效应计算有效值。‎ ‎4．其他情况的有效值一般不能进行定量计算，但有的可以与正弦式交变电流定性比较。如图1交变电流与如图2正弦式交变电流比较，可知其有效值小于Im。‎ 　[2016·唐山模拟]一个U形金属线框在匀强磁场中绕OO′轴以相同的角速度匀速转动，通过导线给同一电阻R供电，如图甲、乙所示，除电阻R外，电路中其他部分电阻忽略不计。其中甲图中OO′轴右侧有磁场，乙图中整个空间均有磁场，两磁场磁感应强度相同。则甲、乙两图中交流电流表的示数之比为(　　)‎ A．1∶ B．1∶2 C．1∶4 D．1∶1‎ 答案　A 解析　题图甲中的磁场只在OO′轴的右侧，所以线框只在半周期内有感应电流产生，如图甲，电流表测的是有效值，所以I＝。题图乙中的磁场布满整个空间，线框中产生的感应电流如图乙，所以I′＝，则I∶I′＝1∶，即选项A正确。‎ ‎1．模型构建 发电机模型是高考中以电磁感应为背景命题的常见模型，凡是在外力作用下做切割磁感线运动而产生感应电流的导体均可看成发电机模型；凡在安培力作用下在磁场中运动的通电导体均可看成电动机模型。‎ ‎2．模型条件 ‎3．模型特点 闭合线圈在磁场中受外力转动产生感应电动势，产生感应电流，与外电路连接，消耗机械能转化为电能。涉及知识为法拉第电磁感应定律、楞次定律、闭合电路欧姆定律、交变电流的“四值”等。‎ 如图所示，N＝50匝的矩形线圈abcd，ab边长l1＝20 cm，ad边长l2＝25 cm，放在磁感应强度B＝0.4 T的匀强磁场中，外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n＝3000 r/min的转速匀速转动，线圈电阻r＝1 Ω，外电路电阻R＝9 Ω，t＝0时，线圈平面与磁感线平行，ab边正转出纸外、cd边正转入纸里。‎ ‎(1)在图中标出t＝0时感应电流的方向；‎ ‎(2)写出线圈感应电动势的瞬时表达式；‎ ‎(3)线圈转一圈外力做功多大？‎ ‎(4)从图示位置转过90°的过程中流过电阻R的电荷量是多大？‎ ‎[答案]　(1)adcba　(2)e＝314cos100πt(V)　(3)98.6 J ‎(4)0.1 C ‎[解析]　(1)根据右手定则可知，线圈感应电流的方向为adcba。‎ ‎(2)n＝3000 r/min＝50 r/s，所以线圈的角速度ω＝2πn＝100π rad/s。‎ 图示位置的感应电动势最大，其大小为Em＝NBSω＝NBl1l2ω，代入数据得Em＝314 V。‎ 电动势的表达式e＝Emcosωt＝314cos100πt(V)。‎ ‎(3)电动势的有效值E＝，线圈匀速转动的周期T＝＝0.02 s，线圈匀速转动一周，外力做功大小等于电功的大小，即W＝I2(R＋r)T＝2(R＋r)T，代入数据得W≈98.6 J。‎ ‎(4)从t＝0时起转过90°的过程中，Δt内流过R的电荷量q＝Δt＝＝，代入数据得q＝0.1 C。‎ ‎1.(多选)如图所示，在匀强磁场中匀速转动的矩形线圈的周期为T，转轴O1O2垂直于磁场方向，线圈电阻为2 Ω。从线圈平面与磁场方向平行时开始计时，线圈转过60°角时的感应电流为1 A。那么(　　)‎ A．线圈消耗的电功率为4 W B．线圈中感应电流的有效值为2 A C．任意时刻线圈中的感应电动势为e＝4cost D．任意时刻穿过线圈的磁通量为Φ＝sint 答案　AC 解析　线圈转动角速度ω＝，线圈平面从与磁场方向平行开始计时，当转过60°角时，电流的瞬时值表达式为i＝Imcos60°＝1 A得Im＝2 A，正弦式交变电流有效值I＝＝ A，故B选项错误；线圈消耗的功率P＝I2R＝4 W，A选项正确；由欧姆定律可知，感应电动势最大值Em＝ImR＝4 V，所以瞬时值表达式为e＝4cost，C选项正确；通过线圈的磁通量Φ＝Φmsinωt＝Φmsint，由感应电动势的最大值Em＝BSω＝Φm×得Φm＝，代入上式得Φ＝sint＝sint，D选项错误。‎ ‎2.如图甲所示，长、宽分别为L1、L2的矩形金属线框位于竖直平面内，其匝数为n，总电阻为r，可绕其竖直中心轴O1O2转动。线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起，并通过电刷和定值电阻R相连。线框所在空间有水平向右均匀分布的磁场，磁感应强度B的大小随时间t的变化关系如图乙所示，其中B0、B1和t1均为已知。在0～t1的时间内，线框保持静止，且线框平面和磁场垂直；t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动。求：‎ ‎(1)0～t1时间内通过电阻R的电流大小？‎ ‎(2)线框匀速转动后，在转动一周的过程中电流通过电阻R产生的热量？‎ ‎(3)线框匀速转动后，从图甲所示位置转过90°的过程中，通过电阻R的电荷量？‎ 答案　(1)　(2)πRω2‎ ‎(3) 解析　(1)0～t1时间内，线框中的感应电动势 E＝n＝ 根据闭合电路欧姆定律可知，通过电阻R的电流 I＝＝。‎ ‎(2)线框匀速转动后产生感应电动势的最大值 Em＝nB1L1L2ω 感应电动势的有效值E＝nB1L1L2ω 通过电阻R的电流的有效值 I＝ 线框转动一周所需的时间t＝ 此过程中，电阻R产生的热量 Q＝I2Rt＝πRω2。‎ ‎(3)线框从图甲所示位置转过90°的过程中，‎ 平均感应电动势＝n＝ 平均感应电流＝＝ 通过电阻R的电荷量q＝Δt＝。‎