高中物理 第五章 曲线运动小结教案 新人教版必修2（通用） 16页

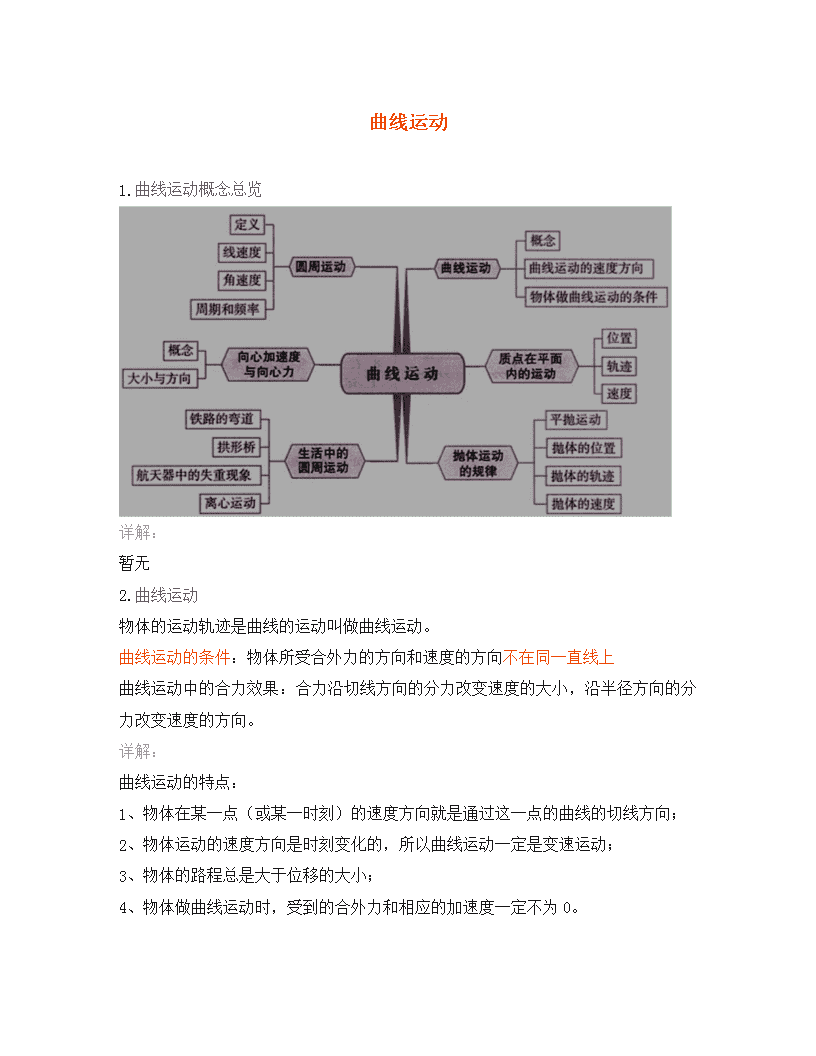
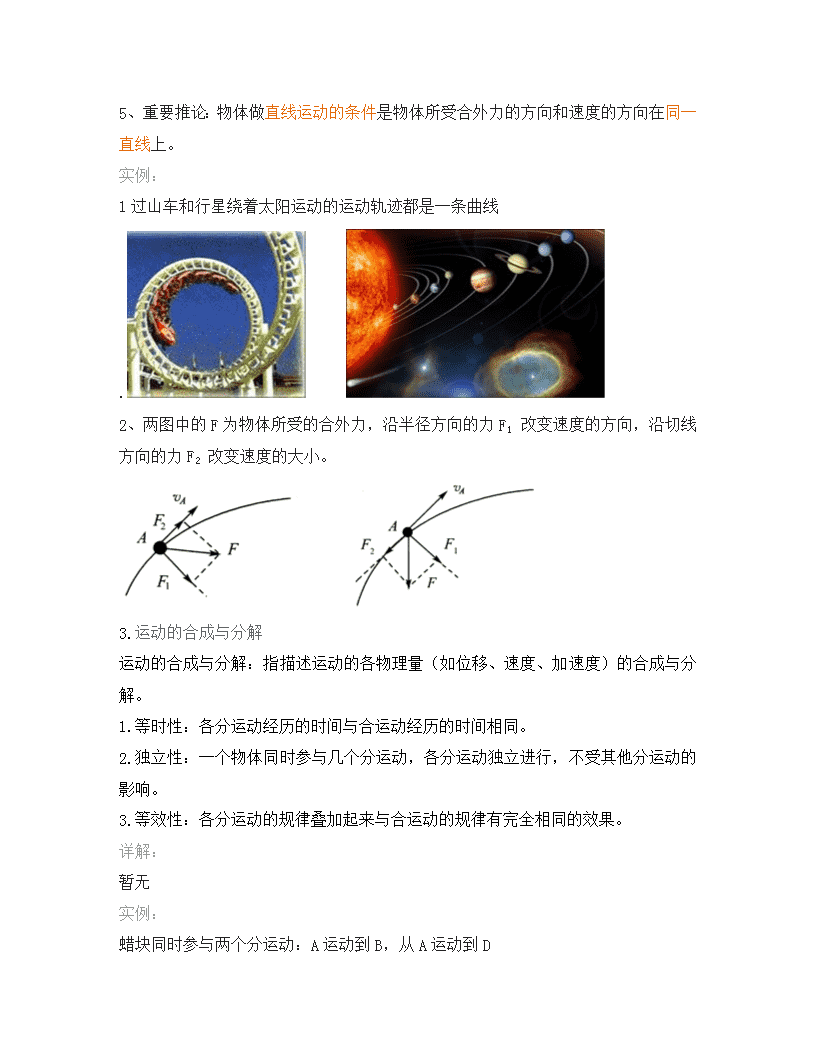
曲线运动 1.曲线运动概念总览 详解： 暂无 2.曲线运动 物体的运动轨迹是曲线的运动叫做曲线运动。 曲线运动的条件：物体所受合外力的方向和速度的方向不在同一直线上 曲线运动中的合力效果：合力沿切线方向的分力改变速度的大小，沿半径方向的分 力改变速度的方向。 详解： 曲线运动的特点： 1、物体在某一点（或某一时刻）的速度方向就是通过这一点的曲线的切线方向； 2、物体运动的速度方向是时刻变化的，所以曲线运动一定是变速运动； 3、物体的路程总是大于位移的大小； 4、物体做曲线运动时，受到的合外力和相应的加速度一定不为 0。 5、重要推论：物体做直线运动的条件是物体所受合外力的方向和速度的方向在同一 直线上。 实例： 1 过山车和行星绕着太阳运动的运动轨迹都是一条曲线 . 2、两图中的 F 为物体所受的合外力，沿半径方向的力 F1 改变速度的方向，沿切线 方向的力 F2 改变速度的大小。 3.运动的合成与分解 运动的合成与分解：指描述运动的各物理量（如位移、速度、加速度）的合成与分 解。 1.等时性：各分运动经历的时间与合运动经历的时间相同。 2.独立性：一个物体同时参与几个分运动，各分运动独立进行，不受其他分运动的 影响。 3.等效性：各分运动的规律叠加起来与合运动的规律有完全相同的效果。 详解： 暂无 实例： 蜡块同时参与两个分运动：A 运动到 B，从 A 运动到 D 蜡块最后的运动表现为：从 A 运动到 C 等时性：分运动 A→B 与 A→D 的时间相等 独立性：分运动 A→B 与 A→D 互不影响 等效性：蜡块先上浮运动再水平运动最后也能到达 C 点 4.矢量运算法则 1.运动的合成： ①如果分运动都在同一直线上，则可选取正方向，与正方向相同的量取正，与正方 向相反的量取负，将矢量运算简化为代数运算。 ②如果分运动互成角度，运动合成时要遵循平行四边形定则。 2.运动的分解： ①确定合速度的方向（就是物体的实际运动方向）； ②根据合速度产生的实际运动效果确定分速度的方向； ③运用平行四边形定则进行分解。 详解： 高中阶段遇到的合成与分解问题，一般都能分解为两个互相垂直的分运动。如平抛 运动与斜抛运动。 5.平抛运动 将物体以一定的初速度沿水平方向抛出，不考虑空气阻力，物体只在重力作用下所 做的运动，叫做平抛运动。 1.存在条件： ①具有水平方向的初速度。 ②只受重力。 2.运动特点：平抛运动是加速度为重力加速度 的匀变速曲线运动，轨迹是抛 物线。 详解： 做平抛运动的物体，水平方向运动不受力，不受竖直方向影响，水平方向做匀速直 线运动；竖直方向运动只受重力，不受水平方向影响，竖直方向做自由落体运动； 物体同时参与水平和竖直方向运动，最后表现出来的合运动为平抛运动。 实例： 1.正例：水平方向初速度，只受重力作用，是平抛运动 2.反例：初速度不沿水平方向，只受重力作用，不是平抛运动 6.平抛运动的公式 水平方向速度保持为 ；水平方向位移为 竖直方向速度随时间变化为 ；竖直方向位移为 物体的合速度为 ；物体的合位移为 合速度与 x 轴夹角： ；合位移与 x 轴夹角： 夹角 θ 与夹角 a 的关系： 详解： 平抛运动中的公式只利用到数学中简单的平面几何关系，认真看图推导就可以得出。 1、运动时间 ，即平抛物体在空中的飞行时间取决于下落的高度，与初速度 无关。 2、落地的水平距离 ,即水平距离与初速度 和下落高度 h 有关，与其他 因素无关。 3、落地速度 ，即落地速度也只与初速度 和下落高度 h 有关。 4、平抛物体的运动中，任意两个时刻的速度变化量 ，方向恒为竖 直向下， 、 、 三个速度矢量构成的三角形一定是直角三角形。 5、平抛物体某时刻的速度反向延长线交 x 轴的坐标值为此时 方向位移的一半。 7.斜抛运动 斜抛运动：物体斜向射出，只在重力作用下，物体作曲线运动。 竖直方向分速度 水平方向分速度 射高为 射程为 详解： 1.射高：在斜抛运动中，物体能达到的最大高度叫做射高。 2.射程：物体从抛出点到落地点的水平距离叫做射程。 8.线速度 做圆周运动的物体通过的弧长 s 与所用时间 t 的比值 符号： 大小： ：做匀速圆周运动的物体通过的弧长，国际单位制单位是 ：通过弧长所用的时间，国际单位制单位是 单位： 方向：沿着圆弧的切线方向 物理意义：描述质点沿圆周运动的快慢 详解： 注意： 1、线速度是矢量，有大小也有方向，是矢量。圆周运动的线速度方向时刻改变，即 使是匀速圆周运动也不是匀速运动，而是变速运动。 2、在实际计算中要将物理量换算成国际单位制单位运算。 实例： 无 9.角速度 半径转过的角度与所用时间的比值 符号： 大小： ：半径转过的角度，国际单位制单位是 ：半径转过的角度所用的时间，国际单位制单位是 T：圆周运动的周期，国际单位制单位是 s f：圆周运动的频率，国际单位制单位是 Hz 单位： 方向：矢量，但高中阶段不讨论其方向问题 物理意义：描述线速度的方向改变的快慢。 10.线速度与角速度的关系 在圆周运动中，线速度的大小等于角速度大小与半径的乘积： 详解： 1. 如图所示，设物体做圆周运动的半径为 r，由 A 运动到 B 的时间为 ，AB 的 弧长为 ，AB 弧对应的圆心角为 ，当 以弧度为单位时， ，以 及 ，解三式得： 2. 当线速度 v 一定时，角速度 与半径 r 成反比；当角速度 一定时，线速度 与半径成正比；当半径 r 一定时，线速度 v 与角速度 成正比。 3. 同轴转动的质点角速度相同；皮带、齿轮、摩擦传动的轮子边缘上的点线速 度相等。 实例： 1.凡是直接用皮带传动（包括链条传动、摩擦传动）的两个轮子，两轮边缘上各点 的线速度大小相等。a 与 c 的线速度相等，a 与 c 的角速度与半径成反比 2.凡是同一个轮轴上（各个轮都绕同一根轴同步转动）的各点角速度相等（轴上的 点除外）。b、c、d 的角速度相等，b、c、d 的线速度与半径成正比 11.匀速圆周运动 在任意相等时间内通过的弧长都相等的圆周运动。 详解： 匀速圆周运动中的速度方向始终在变化，所以匀速圆周运动实际上是匀速率圆周运 动 12.周期 周期性运动每重复一次所需要的时间 符号： 大小： ：频率，国际单位制单位是 单位： 方向：标量，有大小无方向 详解： 对圆周运动而言，周期就是运动一周所用的时间 注意：在实际计算中要将物理量换算成国际单位制单位运算。 实例： 1.地球自转是周期性运动，每重复一次所需要的时间是 24 小时，地球自转的周期是 24 小时 2.分针做的是周期性运动，每转一圈所需要的时间是 1 小时=60 分钟=3600 秒 13.频率 单位时间内运动重复的次数 符号： 大小： ：周期，国际单位制单位是 单位： 方向：标量，有大小，无方向 14.转速 单位时间内的转动圈数。 1.符号：n 2.单位：转/秒，r/s，r/min 3.存在条件：物体要受到向心力的作用 15.线速度、角速度、周期的关系 ：匀速圆周运动的线速度，国际单位制单位是 ：匀速圆周运动的轨道半径，国际单位制单位是 ：匀速圆周运动的角速度，国际单位制单位是 ：匀速圆周运动的周期，国际单位制单位是 ：匀速圆周运动的频率，国际单位制单位是 详解： 注意： 1、在实际计算中要将物理量换算成国际单位制单位运算。 2、在匀速圆周运动中，当半径一定时，线速度与角速度成正比；当角速度一定时， 线速度与半径成正比；当线速度一定时，角速度与半径成反比。 3、如图所示，设物体做圆周运动的半径为 r，由 A 运动到 B 的时间为 ，AB 的弧 长为 ，AB 弧对应的圆心角为 ，当 以弧度为单位时， ，以及 ，解三式得： 4、当线速度 v 一定时，角速度 与半径 r 成反比；当角速度 一定时，线速度与半 径成正比；当半径 r 一定时，线速度 v 与角速度 成正比。 5、同轴转动的质点角速度相同；皮带、齿轮、摩擦传动的轮子边缘上的点线速度相 等。 实例： 1.凡是直接用皮带传动（包括链条传动、摩擦传动）的两个轮子，两轮边缘上各点 的线速度大小相等。a 与 c 的线速度相等，a 与 c 的角速度与半径成反比 2.凡是同一个轮轴上（各个轮都绕同一根轴同步转动）的各点角速度相等（轴上的 点除外）。b、c、d 的角速度相等，b、c、d 的线速度与半径成正比 16.向心力 做圆周运动的物体要受到一个始终指向圆心的等效力的作用 大小： ：匀速圆周运动的线速度，国际单位制单位是 ：匀速圆周运动的轨道半径，国际单位制单位是 ：匀速圆周运动的角速度，国际单位制单位是 ：匀速圆周运动的周期，国际单位制单位是 方向：始终指向圆心 详解： 注意： 1、做匀速圆周运动的物体，向心力就是物体受到的合外力，向心力是效果力。 2、在实际计算中要将物理量换算成国际单位制单位运算。 3、解匀速圆周运动（或竖直方向上圆周运动的最高点和最低点）问题遵循以下步骤： ①确定研究对象（研究对象通常是做圆周运动的那个物体） ②画出研究对象的圆轨迹，找圆心（受力分析后的合外力），求半径 ③对研究对象受力分析，求出合外力，合外力沿半径方向（受力分析不分析向心力） ④合外力提供物体做圆周运动所需要的向心力（合外力与向心力是供需关系） 实例： 1、确定研究对象：研究的是做圆周运动的小球。 2、画圆轨迹，找圆心，求半径，如图。 3、小球受到竖直向下的重力和沿绳子方向的拉力作用，求合力。 4、合力等于向心力。 17.向心加速度 匀速圆周运动的物体的加速度都指向圆心，这个加速度叫做向心加速度。 1.符号：a 2.单位： （米每二次方秒） 3.定义式: 4.匀速圆周运动物体的加速度方向始终指向圆心，不断变化，故匀速圆周运动是非 匀变速曲线运动。 5.当线速度一定时，向心加速度与半径成反比；当角速度一定时，向心加速度与半 径成正比。 6.物理意义：描述线速度方向改变的快慢，只改变线速度方向，不改变其大小（感 谢用户 6691589 提供） 18.汽车过拱形桥最高点受力情况。 汽 车 过 拱 形 桥 最 高 点 时 ， 汽 车 所 受 支 持 力 与 重 力 的 合 力 充 当 向 心 力 。 详解： 解匀速圆周运动（或竖直方向上圆周运动的最高点和最低点）问题遵循以下步骤： ①确定研究对象是汽车 ②画出研究对象的圆轨迹的是公路，找圆心在地底下，半径是最高点到圆心的位置 ③对研究对象受力分析，汽车受到重力 G 和地面对它的支持力 F 求出合外力，合外 力沿半径方向（受力分析不分析向心力） ④合外力提供物体做圆周运动所需要的向心力：汽车过拱形桥最高点时，受重力和 支持力作用，合力充当向心力，指向圆心， ，解得： 可见，汽车对拱形桥压力小于重力，处于失重状态。 19.汽车过凹形桥最低点受力情况。 汽 车 过 凹 形 桥 最 低 点 时 ， 汽 车 所 受 支 持 力 与 重 力 的 合 力 充 当 向 心 力 。 详解： 解匀速圆周运动（或竖直方向上圆周运动的最高点和最低点）问题遵循以下步骤： ①确定研究对象是汽车 ②画出研究对象的圆轨迹，找圆心（受力分析后的合外力），求半径 ③对研究对象受力分析，求出合外力，合外力沿半径方向（受力分析不分析向心力） ④合外力提供物体做圆周运动所需要的向心力（合外力与向心力是供需关系） 汽车过凹形桥最低点时，受重力和支持力作用，合力充当向心力，指向圆心， ，解得： 可见，汽车对凹形桥压力大于重力，处于超重状态。 20.轻绳模型 如图所示，没有物体支撑的小球，在竖直平面内做圆周运动过最高点的情况： 详解： 1.小球过最高点临界条件：小球到达最高点时绳子的拉力（或轨道的弹力）刚好等 于零，小球的重力提供其做圆周运动的向心力，即 是小球通过最高点的最小速度，通常叫临界速度,所以， ； 2.能过最高点的条件： ； 3.不能过最高点的条件： （因为小球还没有到最高点就已脱离了轨道） 21.轻杆模型 如图所示，有物体支撑的小球在竖直平面内做圆周运动过最高点的情况：a、小球固 定在轻杆末端，做圆周运动 b、小球在环形轨道内做圆周运动 c、小球在半圆形路面上运动 详解： 1.小球过最高点临界条件：由于轻杆和管壁的支撑作用，小球恰能达到最高点的临 界速度 ； 2.当时，轻杆对小球有竖直向上的支持力 ，其大小等于小球的重力，即 ； 3.当 时，轻杆对小球有竖直向上的支持力 ，大小随速度的增大而减小， 其取值范围是 ； 4.当 时，轻杆对小球有指向圆心的拉力，其大小随速度的增大而增大。 22.离心运动 做圆周运动的物体，在受到的合外力突然消失或者不足以提供圆周运动所需要的向 心力的情况下，将远离圆心运动，这种运动称为离心运动。 详解： 无 实例： 1.医院和科研机构常用离心分离器加快液体中悬浮微粒的沉淀。 2.洗衣机的脱水筒也是利用离心运动原理设计的。 3.离心水泵也是利用离心运动原理设计的。 4.危害：飞机攀高或翻飞旋转时，离心运动会造成飞行员过荷现象。 防护方法：通过训练，可以减轻离心运动对人体的伤害。 5.危害：汽车在水平路面转弯时所需的向心力大于最大静摩擦力，汽车将做离心运 动而造成事故。 防护方法：为了预防事故的发生，拐弯时应放慢行车速度。