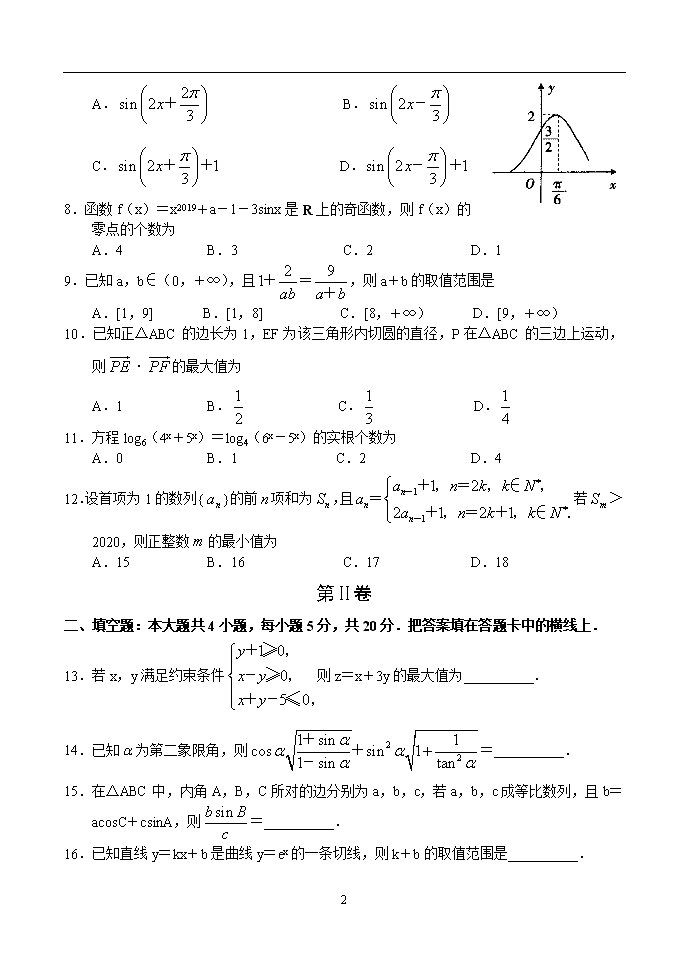河南、河北两省重点高中2020届高三上学期阶段性考试（三）——数学(理) 4页

河南、河北两省重点高中2020届高三阶段性考试（三）‎ 数 学（理科）‎ 考生注意：‎ ‎ 1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟．‎ ‎ 2．请将各题答案填写在答题卡上．‎ ‎ 3．本试卷主要考试内容：复数，集合与常用逻辑用语，函数与导数，三角与向量，数列，不等式．‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知全集U＝{0，1，2，3，4，5，6}，集合A＝{x｜1≤x≤4，x∈N}，B＝{x｜6＜2x＜33，x∈N}，则（CUA）∩B＝‎ ‎ A．{0，5，6} B．{0，5} C．{1} D．{5}‎ ‎2．复数的虚部为 ‎ A．－1 B．1 C．－i D．i ‎3．在公比为2的等比数列{}中，前项和为，且－＝1，则＋＝‎ ‎ A．5 B．9 C．17 D．33‎ ‎4．已知向量m＝（λ＋1，1），n＝（λ＋2，2），若（2m＋n）∥（m－2n），则λ＝‎ ‎ A．－1 B．0 C．1 D．2‎ ‎5．已知，，k∈Z，则＝‎ ‎ A． B．－ C． D．－‎ ‎6．“a＜－1”是“”的 ‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎7．函数（＞0，｜｜＜）的部分图象如图所示，将f（x）的图象向右平移个单位长度后得函数g（x）的图象，则g（x）＝‎ 4‎ ‎ A． B．‎ ‎ C． D．‎ ‎8．函数f（x）＝x2019＋a－1－3sinx是R上的奇函数，则f（x）的 零点的个数为 A．4 B．3 C．2 D．1‎ ‎9．已知a，b∈（0，＋∞），且，则a＋b的取值范围是 ‎ A．[1，9] B．[1，8] C．[8，＋∞） D．[9，＋∞）‎ ‎10．已知正△ABC的边长为1，EF为该三角形内切圆的直径，P在△ABC的三边上运动，则·的最大值为 ‎ A．1 B． C． D．‎ ‎11．方程log6（4x＋5x）＝log4（6x－5x）的实根个数为 ‎ A．0 B．1 C．2 D．4‎ ‎12．设首项为1的数列{}的前项和为，且若＞2020，则正整数的最小值为 ‎ A．15 B．16 C．17 D．18‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡中的横线上．‎ ‎13．若x，y满足约束条件则z＝x＋3y的最大值为__________．‎ ‎14．已知为第二象限角，则＝__________．‎ ‎15．在△ABC中，内角A，B，C所对的边分别为a，b，c，若a，b，c成等比数列，且b＝acosC＋csinA，则＝__________．‎ ‎16．已知直线y＝kx＋b是曲线y＝ex的一条切线，则k＋b的取值范围是__________．‎ 4‎ 三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（10分）‎ 已知等比数列{}的公比q＞0，其前项和为，且＝62，，的等差中项为．‎ ‎ （1）求数列{}的通项公式；‎ ‎ （2）设，求数列{}的前项和．‎ ‎18．（12分） ‎ 已知函数 ‎ （1）判断f（x）在（－∞，＋∞）上的奇偶性，并证明之；‎ ‎ （2）求不等式－1＜f（log4x）≤3的解集．‎ ‎19．（12分）‎ ‎ 已知函数．‎ ‎ （1）若，，∈[－，]，求的值；‎ ‎ （2）若动直线x＝t（t∈[0，]）与函数f（x）和函数 的图象分别交于P，Q两点，求线段PQ长度的最大值，并求出此时t的值．‎ ‎20．（12分）‎ ‎ 如图，在平面四边形ABCD中，AB＝，BC＝‎ 4‎ ‎，CA＝3，且角D与角B互补，·＝．‎ ‎ （1）求△ACD的面积；‎ ‎（2）求△ACD的周长．‎ ‎21．（12分）‎ 设a∈R，命题p：函数y＝loga（x3－ax）（a＞0，a≠1）在区间（－，0）内单调递增；q：函数仅在x＝0处有极值．‎ ‎ （1）若命题q是真命题，求a的取值范围；‎ ‎ （2）若命题是真命题，求a的取值范围．‎ ‎22．（12分）‎ 已知a＞0，函数f（x）＝xln x－ax＋1＋a（x－1）2，．‎ ‎ （1）求g（x）的单调区间．‎ ‎ （2）讨论f（x）零点的个数．‎ 4‎